Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

12.9 Phase transformations controlled by a chemical potential 275

∆x

(a) (b)

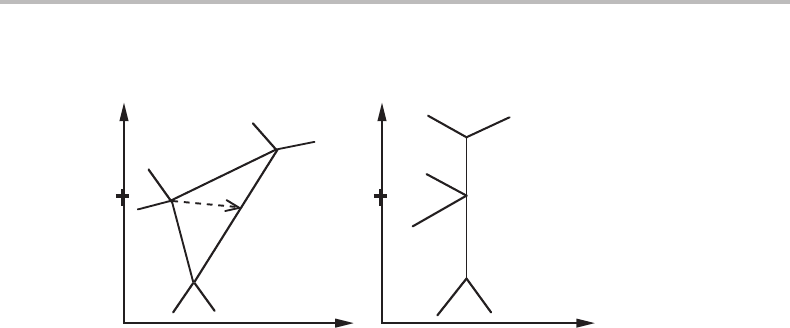
Figure 12.24 Conditions of a transformation under changing the content or chemical potential of

Cinaternary system. T and P are kept constant. The arrow in (a) points towards the C corner.

In (b) it would be horizontal.

Solution

(a) L → α + β(+L); (b) β → L + α(+β); (c) The ﬁrst reaction looks like a eutec-

tic reaction and the second one like a metatectic one although the phase diagram is the

same. The reason is that this is not a sharp transformation and the concepts developed

for sharp transformations cannot be strictly applied.

12.9 Phase transformations controlled by a chemical potential

It is sometimes possible to contain a system inside a wall, which allows some components

to penetrate but not others. In alloy systems it sometimes happens that one component

diffuses much faster than the others. In other cases, one or a few components are volatile

and can easily be exchanged with the surroundings. In these cases it is possible to

produce a phase transformation by gradually changing the chemical potential of the

mobile component but keeping constant the content of all the other components and

also T and P. The conditions may be illustrated by the pair of x

, x

and µ

, u

phase

diagrams in Fig. 12.24(a) and (b), respectively, for a case where p = c and the mobile

component is denoted by C. The arrow in Fig. 12.24(a) represents a discontinuous change

of the C content and is pointing towards the C corner. The u

variable in Fig. 12.24(b)

is explained in Section 4.3.

It is evident that the binary A–B alloy represented by a cross will eventually undergo

a phase transformation γ → α + β if the C content is gradually increased. This may be

indicated in the following way using a reaction formula, γ + C(source) → α + β.

The µ

, u

diagram demonstrates that the transformation will be sharp if the µ

potential can be controlled experimentally and there are no kinetic restrictions. In fact,

the result of such a transformation would be very similar to the result of the well-known

pearlite transformation taking place on a gradual change of temperature in an iron–

carbon alloy. As a consequence, one should expect γ to transform to an intimate mixture

276 Sharp and gradual phase transformations

Ni+BeO

Ni+BeO+NiO

Figure 12.25 See Exercise 12.12.

of the two new phases, α and β,aso-called eutectoid microstructure. This has actually

been observed in many carbon-containing alloyed steels when carburized.

As demonstrated by Fig. 12.24(a), the same transformation is predicted to be gradual if

the C content is increased. However, when the supply of C comes from the surroundings,

there must be a chemical potential differencedriving the diffusionof C. A growing surface

layer of α + β will thus form and the transformation will behave as a microscopically

sharp one. A region has either transformed completely to α + β or is still pure γ.

Exercise 12.12

Figure 12.25 shows a very rough sketch of the Ni–O–Be phase diagram at 1623 K and

1 bar. The hyperbolic solubility curve for BeO in the Ni-rich phase approaches the Ni

corner very closely. It is known that pure Ni oxidizes to NiO in air at 1623 K. Construct

a reasonable proﬁle for the O content from the surface and into the interior of the Ni–Be

alloy denoted by the ﬁlled circle on the u

axis, after some time in air at 1623 K.

Hint

The composition of all layers must lie on the horizontal line through the initial alloy

composition because the u

axis has been used and the diffusion of Be is slow compared

to that of O. Remember that the inward diffusion of O requires a continuous decrease of

the O potential or, more conveniently in the present case, a continuous decrease of the

O content of the Ni phase close to the corner of the diagram (because its Be content is

too low to affect the O potential).

Solution

Suppose an oxide scale of NiO + BeO will form on the surface and also an inner layer

of Ni + BeO. Between them there will be a sharp interface because a three-phase layer

of Ni + NiO + BeO could not exist in a potential gradient. It can exist at a particular O

potential, only, that of the three-phase equilibrium. Furthermore, the average O content

12.9 Phase transformations controlled by a chemical potential 277

Ni+BeO

Ni+BeO+NiO

. .

NiO+BeO

Ni+BeO

Ni (with Be)

Figure 12.26 Solution to Exercise 12.12.

1.0

0.8

0.6

0.4

0.2

0 0.2 0.4 0.6

(a) (b)

Figure 12.27 See Exercise 12.13.

in the layer of Ni + BeO varies quickly close to its inner side where the O solubility

in the Ni phase is low and the solubility line is almost vertical in the phase diagram

(Fig. 12.26). Otherwise, practically no O could diffuse through that part.

Exercise 12.13

The micrograph (Fig. 12.27) shows the structure of an Fe–20 mass% Mo–1 mass% C

alloy at a magniﬁcation of 500×,which has been carburized further at 1273 K and then

quenched. The lower part shows the original structure of M

C particles (black) in a

matrix of γ (now martensite after quenching) and the upper part the new structure. The

278 Sharp and gradual phase transformations

surface is above this picture. Explain the microstructure using the phase diagram which

is for the same temperature.

Hint

From the composition given we calculate u

= 0.13 and u

= 0.05. The value of u

does not change when we add more carbon. The alloy will thus move along a horizontal

line to the right in the phase diagram.

Solution

The alloy is initially in the γ + M

C phase ﬁeld. Moving to the right in the phase

diagram the alloy may enter the three-phase triangle γ + M

C + M

C and approach the

γ + M

C phase ﬁeld. We can thus understand that M

C must transform. A horizontal

line from the M

C corner to the γ + M

C side of the triangle would illustrate the reaction

C + carbon → M

C + γ. This may be regarded as a eutectoid transformation where

carbon plays the role usually played byheat. The conclusion is conﬁrmed by the upper part

of the picture showing regions of a eutectic-like two-phase mixture, evidently M

C + γ

formed from previous M

C particles by the above reaction formula.

Transformations in closed systems

13.1 The phase ﬁeld rule at constant composition

Most of the discussion in the preceding chapter concerned transformations in systems

of constant composition, so-called closed systems. We shall now examine that case in

more detail.

To keep a variable constant means that the phase diagram is sectioned at that value

of the variable. Constant composition means that c −1 molar axes have been sectioned

and thus n

= c − 1 = n

. This can be inserted in the phase ﬁeld rule which is given

by Eqs (10.6) and (10.7). They hold one on each side of a critical p value. Without any

projection the critical value will be

p = 1 + n

+ n

= 1 + 0 + (c − 1) = c. (13.1)

Equation (10.7) will then apply to all p ≤ c, yielding

d = r = c + 1 − n

− n

= c + 1 − (c − 1) − 0 = 2. (13.2)

The two variables are T and P. Equation (10.6) will apply to all p ≥ c, yielding

d = c + 2 − p − n

+ n

= c + 2 − p. (13.3)

This expression resembles Gibbs’ phase rule but it should be emphasized that it applies

to systems with constant composition only for p ≥ c, and in all such cases we obtain

d ≤ 2.

In Sections 13.8 and 13.9 it will be shown that one must take special account of the

presence of congruent transformations. They were neglected when the phase ﬁeld rule

was derived.

Exercise 13.1

Consider the equilibrium CH

↔ C(gr) + 2H

at a constant pressure of 1 bar. Can it

exist at one temperature only or in a range of temperatures?

Hint

Graphite is solid C, CH

and H

are both gaseous but there can be only one gas phase

which is thus a mixture of them.

280 Transformations in closed systems

Solution

We have two components, C and H, c = 2. We have two phases, graphite and gas, p = 2,

and thus p = c and d = c + 2 − p = 2 + 2 −2 = 2. We may vary P and T, i.e. under

any value chosen for P we can still vary T.

Exercise 13.2

Consider the equilibrium CaCO

↔ CaO + CO

in an atmosphere, initially composed

of pure N

. Can the equilibrium exist in a range of temperature if the pressure is kept

constant at 1 bar?

Hint

CaCO

and CaO are two different solid phases. If CO

forms, it will go into the gas and

may form several species, CO

,COand O

, mixed with N

,but there will still be only

one gas phase.

Solution

We have four components, Ca, C, O and N, c = 4. We have three phases, CaCO

, CaO

and gas, p = 3. Thus p < c and the phase ﬁeld rule gives d = 2. For any chosen value

of P we can still vary T.Itshould be emphasized that without N

we could not vary T at

a chosen P.

13.2 Reaction coefﬁcients in sharp transformations for p = c + 1

Keeping P constant in a closed system, i.e. in a system with constant composition, we

have n

= c − 1butn

= c. Instead of Eq. (13.3)weobtain

d = c + 2 − p − n

+ n

= c + 2 − p − c + (c + 1) = c + 1 − p. (13.4)

With p = c + 1 phases, we will thus get a sharp transformation (d = 0) by changing T.

The result would be the same by keeping T constant and varying P. This is why we shall

now discuss the case p = c + 1inmore detail.

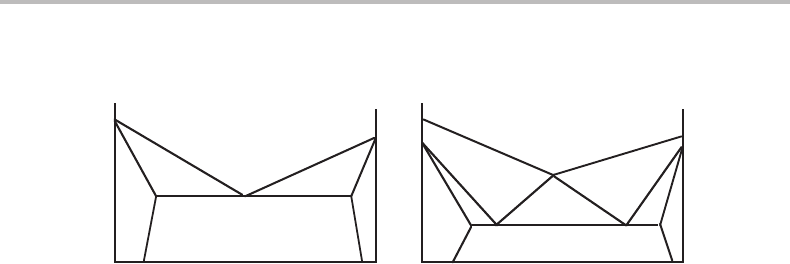
Figure 13.1 shows conditions for a sharp transformation in (a) a binary and (b) a

ternary system. For the binary case (c = 2, p = 3) we can write the reaction formula for

the sharp transformation as follows if we omit any part of an initial phase that remains

when the reaction is completed.

α + β → γ (13.5)

This is independent of whether one passes from α + β to α + γ or from α + β to γ + β,

i.e. independent of whether some α or β will remain.

13.2 Reaction coefﬁcients in sharp transformations for p = c + 1 281

α+β

α+γ+β

α+γ

γ+β

α+β+δ

α+γ

γ+β

αβ

(a)

(b)

Figure 13.1 Conditions for (a) a three-phase transformation in a binary system and (b) a

four-phase transformation in a ternary system at a low constant value of x

. P is constant in both

cases.

It is common to write chemical reactionformulas with reaction coefﬁcients, ν. Accepting

this procedure we can modify the reaction formula for the phase transformation and make

it more quantitative,

α + ν

β = ν

γ. (13.6)

It expresses the fact that ν

moles of the α phase react with ν

moles of the β phase to

form ν

moles of the γ phase. As an example we may consider the oxidation of solid Ag

by gaseous O

4Ag + 1O

= 2Ag

O. (13.7)

In this simple case the reaction coefﬁcients can be given as small integers. In the general

case this is not possible since the phases are not always stoichiometric.

By making the reaction coefﬁcients negative for all the reactants and positive for all

the products we can simply write the formula as ν

J = 0. The ν

values will represent

the relative amounts of the phases taking part in the reaction, for instance expressed as

formula units. Naturally, the ν

values must be such that mass balance is fulﬁlled for

each component i,



= 0 for each component i, (13.8)

where a

is the number of i atoms per formula unit of phase j.Weare considering a

sharp phase transformation with p = c +1 and we thus have a system of c equations

with p = c + 1 coefﬁcients each and in the form of a (c + 1) ×c matrix. By excluding

the jth column of coefﬁcients one obtains a c × c determinant and the value of each ν

is given by such a determinant.

= (−1)

j−1



..a

j−1

j+1

..a



. (13.9)

282 Transformations in closed systems

It is easy to see that the above condition is fulﬁlled by this expression because we ﬁnd



= a



..a



− a



..a



+ ...



..a



= 0. (13.10)

The reason is that two columns in Eq. (13.10)have identical elements because i is one

of the numbers 1 to c.Itshould be noticed that in the calculation of ν

one makes no

distinction between reactants and products. Some of the ν values will turn out positive

and others negative and one may thus identify the members of each group. If the value

for a selected phase turns out with the wrong sign, according to the direction chosen for

the reaction, then one should simply change all the signs.

When non-stoichiometric phases are involved it may be convenient to identify the a

coefﬁcients with the molar contents x

.Weget, for instance,

= (−1)

1−1



..x



..x



. (13.11)

The reaction coefﬁcients of a sharp phase transformation can be used for evaluating the

change of any molar quantity, X

, during the transformation. We obtain

X





..a



. (13.12)

This value refers to 1 mole of the reaction formula, as deﬁned by the reaction coefﬁcients.

It must be emphasized that the present discussion only applies to phase equilibria with

p = c + 1, i.e. phase equilibria which are univariant in the complete phase diagram. That

is exactly the case considered in Section 8.8. There Eq. (8.39)was derived which can be

written as



..x



dT /T =



..x



dP. (13.13)

It can now be transformed into the simpler form

H

V

. (13.14)

Consequently, this simple expression holds for any univariant equilibrium and not only

for the two-phase equilibrium considered initially in Section 8.3.

Exercise 13.3

Prove Kirchhoff’s law for a reaction between well-deﬁned substances, (∂H/∂T )

C

Hint

Forwell deﬁned substances all ν

are ﬁxed. Express H in terms of H

for the various

substances and the reaction coefﬁcients.

13.3 Graphical evaluation of reaction coefﬁcients 283

Solution

H = ν

;(∂H/∂T )

= (∂ν

/∂T )

= ν

(∂ H

/∂T )

= ν

C

but only because (∂ν

/dT )

= 0 for well-deﬁned substances.

Exercise 13.4

From dilatometric measurements on the pearlite transformation in the Fe–C system at

1 bar we know T = 1000 K and V

= 0.047 cm

/mol and from calorimetric measure-

ments we know that H

=−4540 J/mol. Calculate the pressure dependence of the

transformation temperature.

Hint

The pearlite transformation is γ → α + Fe

C. First check how many degrees of freedom

this equilibrium has in a binary system. Then use an equation derived for that particular

case.

Solution

We have p = 3 and c = 2 and, thus, p = c + 1, i.e. a sharp transformation at con-

stant P.For that case we get the slope dT /dP = T V

/H

= 1000 × 0.047 ×

−6

/(−4540) =−1.04 × 10

−8

K/Pa =−10

−3

K/bar.

13.3 Graphical evaluation of reaction coefﬁcients

The reaction coefﬁcients for a sharp transformation in a closed system can also be

evaluated graphically using the lever rule. For c = 2, p = 3 one of the phases transforms

into a mixture of the other two. The composition of the ﬁrst phase is thus equal to the

average composition of the other two and the lever rule can be applied directly. For

c = 3, p = 4 there are three different cases as illustrated by Fig. 12.9.Inclass I and

class III reactions one of the phases may transform into a mixture of the other three

and, again, the composition of the ﬁrst phase is equal to the average composition of the

others. If the reaction coefﬁcient of the ﬁrst phase is taken as −1, the coefﬁcients of the

other phases are obtained as the fractions of the subsystems using one of the methods

described in Fig. 4.5.

Class II can be handled by considering that a mixture of two phases will transform into

a mixture of the remaining two phases. Evidently, the compositions of the two mixtures

must be equal and should thus fall on the point of intersection between the two diagonals,

point ‘i’ in Fig. 13.2.

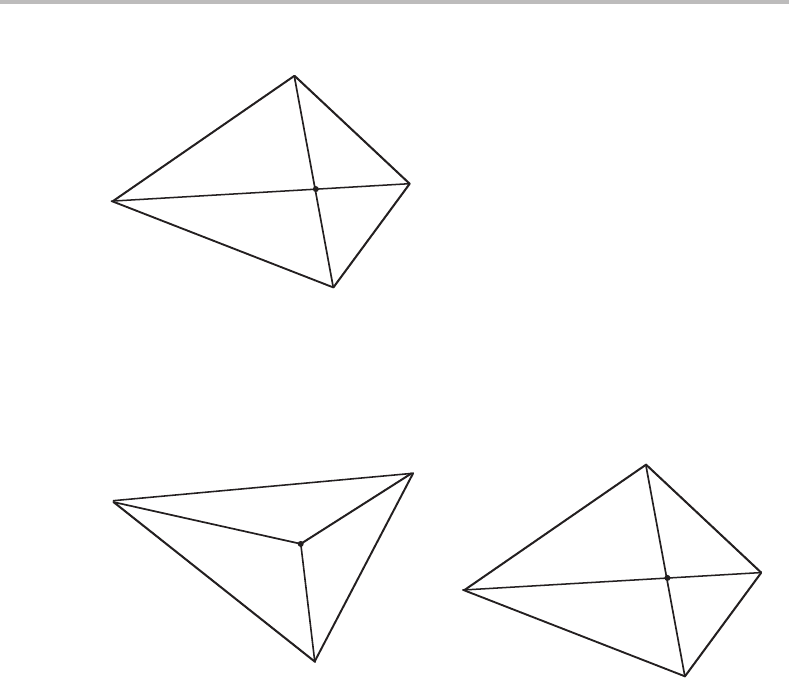
If the average composition of the system does not coincide with the ﬁrst phase dis-

cussed for classes I and III, then it falls inside one of the three smaller triangles (see

the diagram for δ → α + β + γ in Fig. 13.3(a)). The composition of δ will be adjusted

284 Transformations in closed systems

Figure 13.2 Compositions of phases in a class II reaction in a ternary system. The weighted

average of the two reacting phases, say α and γ, must fall on the intersection between the

diagonals and so must the weighted average of the two product phases, say β and δ.

(a) (b)

Figure 13.3 Relations between phase compositions in (a) a class I or III transformation and in (b)

a class II transformation.

by precipitation of ﬁrst one and later two of the other phases in the small triangle as

the temperature of the four-phase plane is approached. There the rest of it will fall on

the δ point in the diagram and will transform to a mixture of the other three phases.

The microstructure will show a matrix with a characteristic pattern of the three-phase

mixture in which one can see imbedded one-phase regions of the ﬁrst phase to precipitate

and eutectoid regions of the two co-precipitated phases. If the average composition falls

outside the triangular four-phase plane, then the δ phase will never reach the four-phase

plane.

For class II there are four alternatives and it is interesting to note that the range

of existence of each one of the four phases extends to both sides of the four-phase

plane. In Fig. 13.3(b) the three-phase ﬁelds α + β + δ and β + δ + γ extend to one side

and α + β + γ and α + γ + δ extend to the other side. If a specimen with an average

composition falling inside the α − β − i triangle is approaching the four-phase plane

from the ﬁrst side, then it will contain a mixture of α + β + δ when reaching the four-

phase plane. From a mass balance point of view it may be regarded as a mixture of β + δ

falling on point i and some extra amounts of α and β. The mixture of β + δ will