Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 111

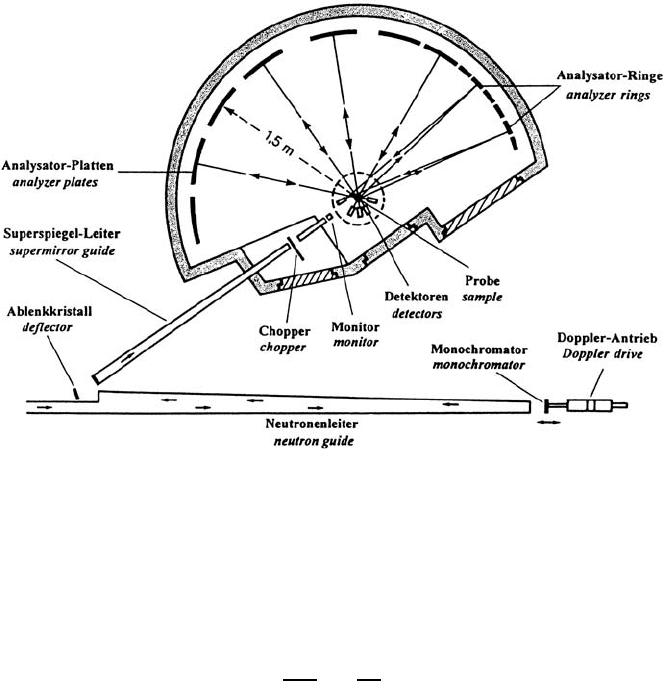
Fig. 3.8. Backscattering spectrometer at the J¨ulich FRJ-2 reactor. The Bragg

angles at the silicon single crystals (before and after scattering of the neutrons by

the sample) are close to 90

◦

. Other well-known spectrometers of this type are IN10,

IN13 and IN16 at the ILL in Grenoble, and HFBS at NIST in Gaithersburg.

scan is performed by a Doppler drive, moving the monochromator crystal

with a speed v

. The resulting energy shift is [37]

δE

(3.44)

which yields an energy window of δE

= ±15 µeV for v

=2.5 m/s and

=6.3

Fig. 3.8 shows the backscattering spectrometer built at the J¨ulich FRJ-2

reactor. Cold neutrons are produced in a liquid hydrogen source which mod-

erates the neutrons from the D

O reﬂector and transfers the spectrum from

an eﬀective temperature close to room temperature to about 20 to 40 K. The

resulting intensity gain factor in the desired low-energy spectrum is between

7 and 15. The monochromator crystal (10×10 cm

) is ﬁxed on a sinusoidally

moving Doppler drive. The backscattered neutrons are separated from the in-

cident beam by a (broad band) copper single crystal which reﬂects the whole

energy range of about 30 µeV covered by the Doppler motion. The monochro-

matic neutrons, falling onto the sample, being scattered, and ﬁnally detected,

are individually labeled with the corresponding instantaneous speed of the

Doppler drive. The neutrons scattered by the sample are backscattered by

spherical shells of Si crystals and thus focussed into a set of BF

counters.

112 Tasso Springer and Ruep E. Lechner

Fig. 3.9. Typical quasielastic spectra measured with backscattering spectrometry

in the µeV-region on hydrogen diﬀusing in ZrV

for several scattering vectors Q.

Dashed narrow line: Resolution curve of the spectrometer. Dashed broad line: Qua-

sielastic component due to rapid non-diﬀusive motion at large Q (see Sect. 3.5) [38].

Each counter corresponds to a certain scattering angle or Q-value. To avoid

that the scattered neutrons are directly falling onto the counters (before they

have been ﬁltered by the Si analyzers), the incident beam is periodically in-

terrupted by a chopper, in phase with the Doppler movement. Only when the

beam is closed, the consecutively scattered and analyzed neutrons reach the

counters. Fig. 9 presents typical quasielastic spectra for hydrogen diﬀusing

in an alloy, measured with µeV resolution at diﬀerent Q values.

Very often the energy range is too narrow. The reﬂected neutron energy

can be additionally shifted by heating the monochromator, thus increasing

the lattice parameter, and/or using monochromators whose lattice parameter

is somewhat smaller or bigger than that of the silicon analyzer [39]. In this

way, the range of the spectrometer (and also the resolution) can be adapted

to the problems.

Sometimes, backscattering spectrometers are used with the Doppler drive

at rest. In such a measurement one determines the intensity for the spectro-

meter set at ω = 0, i.e. the convolution integral I(ω =0)=(S ⊗R), where S

is the neutron scattering function and R is the energy resolution function. For

a Lorentzian-shaped spectrum as in (3.31), S

inc

(Q, ω)=(Γ/π)/(Γ

+ ω

and assuming a Lorentzian shape for the resolution function as well (approx-

imately valid for the classical BSC spectrometer), with a width (HWHM)

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 113

∆(ω), one obtains for the measured intensity

I(Q, ω =0,T)=

(Γ (Q, T )+∆(ω))

. (3.45)

Let us now, for the purpose of discussion, assume that in our example a single

relaxation process (responsible for the Lorentzian line shape) is active over

the whole temperature range considered, and that it shows an Arrhenius type

behaviour. Then, for suﬃciently small temperatures, the quasielastic line falls

entirely into the energy resolution window. Therefore, it does not cause any

measurable quasielastic broadening. Then one gets for the “window intensity”

I(Q, ω =0,T)=1/(π∆(ω)). (3.46)

With increasing temperature, the line width Γ grows, and ﬁnally becomes

larger than the window ∆(ω); the measured intensity of the window scan

then reveals a “stepwise” decrease. Therefore, a simple temperature scan al-

lows one to get a qualitative survey of the diﬀusion or relaxation processes in

the sample as a function of temperature (ﬁxed-window method: ﬁrst measure-

ments with this method were carried out by Alefeld et al. on N(CH

)

MnCl

[40], tetramethyllead [41], and (NH

)

SnCl

[42]; see also [21] p. 284).

The intensity “step” represents a (purely methodical) transition from non-

observability at low T to observability at high T of the relaxation process.

From the shape of this step the relaxation time of the single process can

easily be determined. Let us consider this problem for the more complex

situation of a localized diﬀusive process, implying an elastic in addition to

a quasielastic Lorentzian component. Here the same experimental method

can be applied. If the attenuating eﬀect of (harmonic) vibrational motions

is described by a classical Debye-Waller factor, the temperature-dependent

window-scan intensity, in logarithmic form, is given by [43]

ln(I)=−CTQ

+ln(A(Q)/(π∆(ω)) + (1 − A(Q))/[π(2/τ

+ ∆(ω))] .

(3.47)

Here CT is the vibrational mean square displacement (with a temperature

coeﬃcient C), A(Q) is the EISF, and τ

is the relaxation time (for a two-site

jump model in our example). It is interesting to note that the observability

transition described by (3.47) can be used for the determination of the EISF,

provided that the mechanism does not change in the T -region of the step.

For this purpose, the measured low-temperature straight line of ln(I)vs.T

is extrapolated to high T and compared with the measured high-temperature

line; the latter is obtained, when due to strongly increased line-broadening,

the quasielastic contribution to the intensity becomes negligible. A simple

division of the intensities yields the EISF according to the equation [43]

ln[A(Q)/(π∆(ω))] = [ln(I)

high T

] − [ln(I)

extrapol

low T

] . (3.48)

As an example of such a measurement, Fig. 3.10 shows the result obtained

for the solid-state protonic conductor CsOH · H

O (see Sect. 3.9).

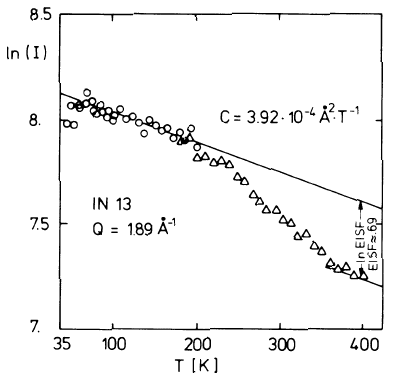
114 Tasso Springer and Ruep E. Lechner

Fig. 3.10. Example of an apparent observability transition exhibited experimen-

tally by the elastic intensity of CsOH ·H

O measured as a function of temperature:

Logarithmic plot of the elastic-window intensity obtained with IN13 (ILL Grenoble)

at Q =1.89

−1

. The straight lines show the variation of the Debye-Waller factor

in the limits of low T and high T , respectively. The logarithm of the EISF is simply

the diﬀerence between the values of the two lines at a given temperature [43].

Last, but not least, the TOF-XTL technique should be mentioned. This

type of hybrid instrument, employing a pulsed polychromatic (“white”) inci-

dent beam and single-crystals in BSC-geometry as analyzing ﬁlters, is repre-

sented by IRIS [44] at RAL in Chilton. It is well adapted to the time-structure

of spallation neutron sources. The energies of the incident neutrons are mea-

sured with time-of-ﬂight techniques, while the energy of scattered neutrons

is ﬁxed by the analyzers. Depending on the type of crystals used, several

discrete values of energy resolution in the range from about 1 to 16 µeV are

achieved. An example of application is given in Sect. 3.11.

Let us ﬁnally mention a few technical points concerning the analysis of

QENS data. An important problem in the evaluation of quasielastic neutron

spectra is the accurate consideration of the experimental resolution. Although

straightforward, this is complex, if the spectrum is a sum of several quasi-

elastic components, eventually superimposed by a purely elastic line, either

due to the fact that the diﬀusive motion is localized, or caused by para-

sitic incoherent scattering on the host material in which the particles diﬀuse.

The measured spectra are convolutions of the dynamic structure factor with

the resolution function. Since a direct deconvolution often encounters prac-

tical diﬃculties, in a typical analysis the data are usually not corrected for

resolution, but an inverse procedure is employed. It consists in folding the

theoretical model with the measured resolution function and comparing the

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 115

result to the measured spectra. This procedure, which amounts to an indirect

deconvolution, is well-known, and standard software packages are available

in the Neutron Scattering Centers.

Another problem is multiple scattering (MSC). In principle, a neutron

reaching the detector, may have been scattered in the sample once , twice, or

even several times. For a given nominal scattering angle ϕ or nominal Q value

∼

(4π/λ)sin(ϕ/2)) the convolutions of two or more quasielastic spectra

are then superimposed on the single-scattering data. The MSC components

should be minimized by using suﬃciently thin samples. Nevertheless, a nu-

merical correction is often necessary. Analytical methods [45] directly applied

to the theoretical models, and model-independent Monte-Carlo techniques

(see for instance [46], [47]) are employed for this purpose.

The third problem is calibration, which means the absolute determination

of the scattered intensity, instead of quoting “arbitrary units”. Calibration is

performed, for instance, by a vanadium scatterer which has the same geom-

etry as the sample itself, and whose incoherent scattering cross-section is

well-known (provided that there is no hydrogen contamination).

For many elements coherent and incoherent scattering coexists, and it is

diﬃcult to separate the contributions S

coh

(Q,ω)andS

inc

(Q,ω). Spin inco-

herent scattering causes (2/3)[σ

inc

/(σ

inc

+ σ

coh

)] of the neutrons to ﬂip their

spin in a polarized neutron beam, whereas coherent scattering occurs without

spin ﬂip. The high intensity of polarized beams available at the reactor in the

Institut Laue-Langevin in Grenoble allows one to apply this property for a

direct separation of the coherent and incoherent contributions, by orienting

spin analyzer and polarizer parallel and anti-parallel ( [48], see also [49] and

Sect. 13.2.2 in Chap. 13).

More information on modern QENS spectrometers can be found in the

Instrumentation Booklets of the Neutron Scattering Centers (ILL in Greno-

ble, LLB in Saclay, BENSC at HMI in Berlin, ISIS at RAL in Chilton, NIST

in Gaithersburg, FZ J¨ulich, IPNS at Argonne).

3.5 Hydrogen Diﬀusion in Metals and in Metallic Alloys

The ﬁrst investigations of quasielastic scattering on diﬀusing atoms were

performed by Sk¨old and Nelin [50] on palladium hydride where the H atoms

diﬀuse over an interstitial lattice. The experiments on powder samples indi-

cate clearly that, for small scattering vectors Q, the diﬀusion coeﬃcient is

obtained following (3.33). For larger Q, the data are consistent with diﬀusion

on an octahedral lattice (see Fig. 3.11). More recent experiments on palla-

dium single crystals are shown in Fig. 3.12 [51]. The results agree very well

with the Chudley-Elliott model. Results from computer simulations by Li and

Wahnstr¨om [52] are included in the ﬁgure, where the hydrogen potential was

modelled in the adiabatic Born-Oppenheimer approximation, tested with the

help of the known vibrational frequencies of the dissolved hydrogen. These

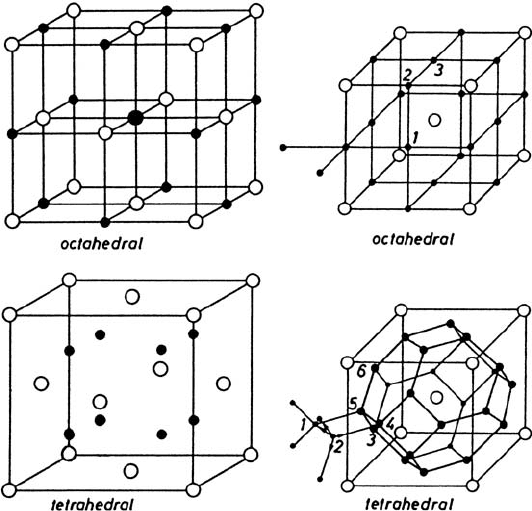
116 Tasso Springer and Ruep E. Lechner

Fig. 3.11. Tetrahedral and octahedral interstitial sites (•) for fcc (left) and bcc

(right) host lattices. The sites can be occupied by H atoms. The 6 (3) non-equivalent

sublattices in the bcc (fcc) lattice are labeled. The bcc tetrahedral sites are con-

nected by [110] jump vectors.

calculations strongly deviate from the Chudley-Elliott model and from the

experiments. Agreement between the computer simulations and the experi-

ments was obtained by introducing a dissipative force which is supposed to

follow from the interaction of the protons with the conduction electrons.

The process of diﬀusive motions of hydrogen in bcc metals, in particu-

lar in niobium hydride, is complicated and not yet fully understood, despite

the great number of investigations published so far (e.g. [53–55]). Hydro-

gen atoms occupy tetrahedral sites in the bcc lattice (Fig. 3.11) forming six

non-equivalent sublattices. Consequently, the quasielastic line is a superposi-

tion of six Lorentzians and it is ﬁnally dominated by a single Lorentzian for

Q → 0 whose width is Q

. A comparison between quasielastic scattering

experiments and theory is shown in Fig. 3.13. For simplicity, only the half

width of the combined quasielastic line is used [53]. Obviously, for larger Q

the eﬀective width is considerably smaller than expected from the simple

Chudley-Elliott model. One speculates that this might be due to an eﬀective

jump distance larger than expected from the lattice parameters.

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 117

Fig. 3.12. Quasielastic width in units of D

(a = lattice constant) for H dif-

fusion on octahedral sites in fcc Pd. • Quasielastic experiments with Q parallel

[100] (a) and [110] (b). Dashed: Chudley-Elliott theory; triangles: computer sim-

ulation without friction force due to interaction between protons and conduction

electrons; squares: with such a friction force [51, 52].

Fig. 3.13. Quasielastic width for cubic α-NbH

0.02

with Γ (Q) determined from the

composite spectrum. Ψ = angle between [110] and k

. (1) Chudley-Elliott model

(tetrahedral jump vectors, Fig. 3.11). (2) Correlated double jumps. (3) Jump se-

quences (from [54]).

The following model [54] describes the obtained experimental results. At

elevated temperature the hydrogen alternates between a ‘state’ where it is

localized by the strong elastic relaxation of the surrounding host lattice, with a

rest time τ

,andamobile state, where it follows a rapid sequence of two, three

or more jumps between adjacent tetrahedral sites, with a rate several times

larger than 1/τ

. This memory eﬀect follows from the relaxation of the host

lattice. The hydrogen ion on a tetrahedral site creates an elastic distortion of

tetragonal symmetry as in Fig. 3.14 with a certain axis shown in this ﬁgure.

A jump leading to an adjacent site reorients this axis by 90

◦

, and a ﬁnite

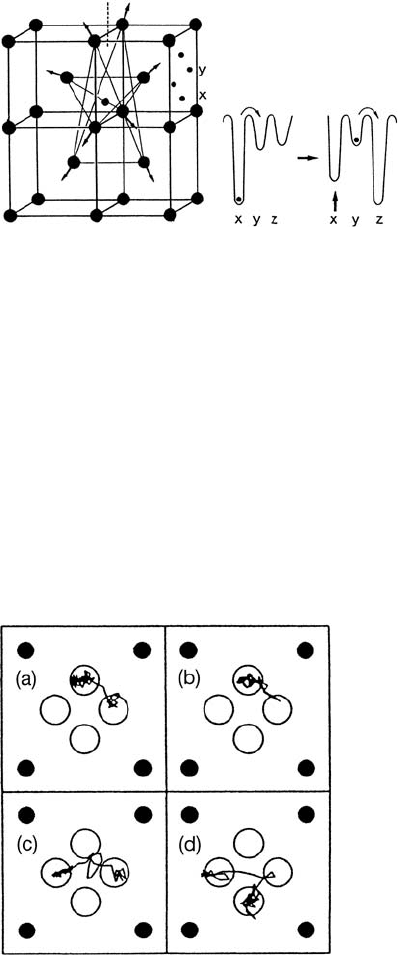
118 Tasso Springer and Ruep E. Lechner

Fig. 3.14. Left: Atomic displacements around a H atom on a tetrahedral site x in

the Nb lattice. A nearest neighbour jump (e.g. from site x to y) causes a rotation of

the symmetry axis (dashed) by 90

◦

with a relaxation time of the displacement ﬁeld

∼

−12

s. Right: Potential for sequence of correlated jumps with incomplete

relaxation of the potential minima (see also Sect. 18.3 in Chap. 18).

time τ

is required until the new arrangement of the surrounding lattice is

entirely restored. Small-polaron theory allows a calculation of this time with

∼ 10

−12

s [56]. Consequently, for the ﬁrst moment (i.e. for t  τ

), the

activation barrier opposing a hydrogen ion to leave the site is lower than for

a fully relaxed site. Obviously, there is an enhanced probability to leave this

shallow site before full relaxation has occurred. This favours correlated jump

sequences, as well as back jumps to the original site. Fig. 3.15 shows typical

hydrogen trajectories in Nb from molecular dynamics calculations [57].

Fig. 3.15. Typical trajectories of hydrogen motion projected in a (100) plane of the

Nb lattice from molecular dynamics calculation over a time interval of 5·10

−12

s [57].

Correlated “forward” and “backward” jumps can be identiﬁed.

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 119

Two striking anomalies of the bcc hydrides may be related to the strain

ﬁeld caused by the jumps. (i) Huang scattering (i.e. scattering close to the

Bragg lines) probes the symmetry of the long-range strain ﬁeld due to the

dissolved H atoms [58]. X-ray experiments on niobium hydride show that

the strain ﬁeld is practically cubic. (ii) The inelastic Snoek relaxation of the

bcc Nb hydride is proportional to the squared diﬀerence of the two diagonal

components of the Kanzaki double force tensor (A–B)

. Also the Snoek relax-

ation experiments lead to the conclusion of a nearly cubic strain ﬁeld [59]. If

the time of a jump sequence is comparable to or shorter than the long-range

lattice relaxation, the contributions due to the occupancy of an occupied

site and of previously occupied sites are superimposed. Since the orientation

of the strain ﬁelds are mutually orthogonal, the resulting long-range ﬁeld is

supposed to approach a distribution close to cubic symmetry.

A detailed experimental and theoretical analysis by Dosch et al. [55] treats

the dynamics of the strain ﬁeld. For the ﬁrst time, these authors were able

to observe the quasielastic scattering due to the strain ﬁeld ﬂuctuations orig-

inating from hydrogen jumps. From these results the authors conclude the

existence of very fast back- and forth-jumps between adjacent sites; also these

could be responsible for a reduction of the tetragonal components in the

double force tensor and, therefore, of the long-range ﬁeld. Such fast “local”

motions distribute the proton over adjacent sites. If this motion is resolved

energetically, it should cause a Q-dependent factor in addition to the Debye-

Waller factor, exp(−u

Q

), where u

 is the mean square vibrational am-

plitude. This would amount to a very steep decay of the quasielastic intensity

with increasing Q, and would have to be identiﬁed with the elastic incoher-

ent structure factor (EISF) as deﬁned in (3.16)-(3.18). The interpretation of

Debye-Waller factor and EISF needs special attention. The hydrogen motion

in the 10

−12

s regime can be identiﬁed by a ﬁt of a suitable theoretical func-

tion S

ﬁt

(Q, ω) to the experimental data, in an experimentally limited window

−ω

max

≤ ω ≤ ω

max

. The corresponding quasielastic intensity is then cal-

culated by integration, assuming that S

ﬁt

also reproduces suﬃciently well the

contribution of the diﬀusive motion to the scattered intensity outside of the

ﬁtting region:

I(Q)=



∞

−∞

ﬁt

(Q, ω)dω. (3.49)

If there are fast motions not covered by S

ﬁt

(Q, ω), e.g. the rapid back- and

forth-jumps as described in [55], in the 10

−13

to 10

−14

s region, the quasi-

elastic intensity should read

I(Q)=e

−u

Q

F (Q) . (3.50)

The ﬁrst factor is the usual Debye-Waller factor of the proton due to phonons

and localized vibrational modes, and F (Q) is the EISF, i.e. the Fourier trans-

form of the proton distribution in space by diﬀusive motions which are faster

than the 10

−12

s jumps.

120 Tasso Springer and Ruep E. Lechner

Table 3.1. Hydrogen diﬀusion coeﬃcients in diﬀerent intermetallic hydrides. For

comparison, the values for dilute PdH

and NbH

are also included.

Specimen D

(cm

/s) E

act

(meV) D

300 K

(cm

/s) Reference

PdH

x→0

5.3 · 10

−3

236 5.7 · 10

−7

[60]

NbH

x→0,T >250K

3.6 · 10

−4

108 5.5 · 10

−6

[61]

NiH

2.0 · 10

−4

345 3.2 · 10

−10

[62]

TiFeH 7.2 · 10

−4

500 2.9 · 10

−12

[63]

TiFeH 4.2 · 10

−7

330 1.2 · 10

−12

[64]

LaNi

3.2 · 10

−4

249 2.1 · 10

−8

[65]

LaNi

2.1 · 10

−3

275 5.0 · 10

−8

[66]

TiCr

1.8

2.6

270 [67]

1.2

1.8

5.9 · 10

−4

225 9.8 · 10

−8

[68]

0.8

0.2

CrMnH

3.1 · 10

−4

220 6.2 · 10

−8

[69]

NiH

0.3

6.7 · 10

−5

280 1.3 · 10

−9

[70]

Numerous quasielastic scattering studies were performed on alloy hydrides

which reveal high solubilities and mobilities of the hydrogen atoms. One

objective of the investigations was the determination of the bulk self-diﬀusion

coeﬃcient from quasielastic experiments at small Q. Table 3.1 summarizes

results from such investigations, namely D

for 300 K and the parameters for

an Arrhenius law describing the temperature dependence, namely

(T )=D

−E

act

. (3.51)

With these bulk diﬀusion coeﬃcients the hydrogen absorption or desorption

rate, K

, in a storage powder was calculated and compared with experiments.

For a grain size R one obtains approximately

= π

. (3.52)

For Ti

0.8

1.2

CrMnH

[69] one gets D

=6· 10

−12

/s from quasielastic

scattering; the grain size of the storage powder is R ≈ 0.5 µm. This leads

to a reaction rate of K

= 400 s

−1

, provided that absorption and desorption

is diﬀusion controlled. The measured rate, however, is only 0.1 s

−1

.This

implies that the reaction rate is retarded by the surface and not controlled

by the fast bulk diﬀusion. The opposite situation was found for TiFeH

[63]

where the self-diﬀusion is very slow and the reaction is diﬀusion controlled.

However, if one calculates K

, the resulting value is smaller than measured.

Using metallographic pictures this was explained by microcracks in the grains

which bypass the diﬀusion path. Obviously, quasielastic neutron scattering