Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 101

Let us consider an example, in order to illustrate the implications of ex-

perimental resolution in the study of dynamic structure on the basis of the

Van Hove formalism (see for instance (3.11), (3.13)). We assume, for sim-

plicity, that the scattering particle carries out a random motion described

by a superposition of several components with n diﬀerent rates, λ

, λ

, ...,

. The scattering function will then be a sum of bell-shaped Lorentzians

centered at zero energy transfer (see the following sections). If this quasielas-

tic spectrum is studied with an instrument resolution ∆(ω), the resulting

resolution-broadened spectrum is again a bell-shaped curve, but with a width

larger than ∆(ω). This “quasielastic peak” will be dominated by contribu-

tions from those motions which have rates λ

∼ ∆(ω). While much slower

motions are hidden within the resolution function, much faster motions will

produce only a ﬂat “background” which cannot be easily distinguished from

the usual constant background of the experiment. In order to be able to ex-

tract information on all relevant motional components, one needs to carry

out several measurements with properly chosen resolutions. This procedure

may in practice require the application of more than one type of spectrome-

ter. Quasielastic neutron scattering spectra obtained with one single energy

resolution only usually furnish incomplete information. The analysis may

therefore easily lead to wrong conclusions.

Since ∆(ω) is related in a simple way to the instrumental energy spreads

of incident and scattered neutrons, the observation time, ∆t, is connected

with (although not equal to) the coherence time of the incident neutron

wave packet. The principle of experimental observation time, energy and

Fourier time windows in quasielastic neutron scattering, and their relevance

for the determination of dynamic structure, and especially in problems con-

cerning diﬀusive atomic and molecular motions in condensed matter, has

been discussed more extensively in [16] and [18]. For further detailed liter-

ature related to the Van Hove concept and quasielastic neutron scattering

we refer to the reviews, monographs and books specially devoted to this

topic [3,14, 15, 17, 19–21].

Finally, we note a complication due to the fact that an atomic species

consists of isotopes with diﬀerent scattering lengths b

... and concen-

trations c

.... Therefore the sum in (3.6) includes terms with diﬀerent

scattering lengths, randomly distributed over the sites r

. This randomness

of the amplitudes destroys part of the interference. A similar eﬀect is caused

by the spin of the nuclei and of the neutron, because the scattering length

depends on their relative orientation. This leads to scattering lengths b

and b

−

corresponding to parallel and anti-parallel orientation with fractions

=(I +1)/(2I +1) and c

−

= I/(2I + 1), respectively, where I is the

nuclear spin. If nuclei and/or neutron spins are unpolarized, this gives a ran-

dom distribution of b

and b

−

. Randomness destroys part of the interference

and for ideal disorder the cross section can be separated into a coherent part

with interference terms due to pairs of atoms (including the self-terms) and

102 Tasso Springer and Ruep E. Lechner

an incoherent part where interference between waves scattered by diﬀerent

nuclei has completely cancelled out, such that the diﬀerential cross-section

reads

dΩdω



coh

4π

coh

(Q,ω)+

inc

4π

inc

(Q,ω)

. (3.22)

The coherent scattering function, S

coh

(Q,ω) in the ﬁrst term, is due to

the atom-atom pair-correlations, whereas the incoherent scattering function,

inc

(Q,ω) in the second term

, only conveys self-correlations and therefore

behaves as if not amplitudes but intensities from scattering by diﬀerent nu-

clei had to be added.

One can easily show that the total scattering cross sections σ

coh

and σ

inc

have the following meaning

coh

=4π

with

b =



, (3.23)

inc

=4π



−



with



. (3.24)

In the following section we mainly deal with the incoherent dynamic struc-

ture factor. In particular, for hydrogen the incoherent scattering cross section

is between 10 and 20 times larger than other scattering cross sections, such

that the separation of S

inc

is especially easy. We point out that the speciﬁca-

tion “incoherent” is somewhat misleading. In order to calculate the scattered

intensities the amplitudes have to be added and the sum has to be squared.

Disorder leads to a (partial) cancellation of the cross terms with phase fac-

tors. Consequently, the intensities are summed up with reduced interferences.

The total coherent and incoherent scattering cross-sections are empirically

known and a great number can be found in tables [22](for a review on the

fundamental aspects of neutron-nucleus scattering see [23]).

3.3 The Rate Equation and the Self-Correlation

Function

A model was originally proposed by Chudley and Elliott [24], to obtain the

classical self-correlation function G

(r,t) for an atom diﬀusing on an assumed

quasi-crystalline lattice of a liquid. This so-called CE-model was then widely

used for treating atomic diﬀusion on interstitial lattices in crystals.

We ﬁrst calculate the probability P (r

,t) to ﬁnd the diﬀusing atom on a

site r

of a Bravais lattice at time t, where it spends a time τ on the average.

The time τ

required for the diﬀusive jump from site to site is neglected.

The jumps occur between a given site and its neighbours r

+ d

where

(ν =1, 2,...s) is a set of jump vectors connecting the site with the

neighbours. The master equation for P (r

,t) is then (see Fig. 3.3)

Note that the following notations for the scattering functions (dynamic structure

factors) are customary in the literature : S(Q,ω)orS

coh

(Q,ω) for coherent, and

(Q,ω)orS

inc

(Q,ω) for incoherent scattering.

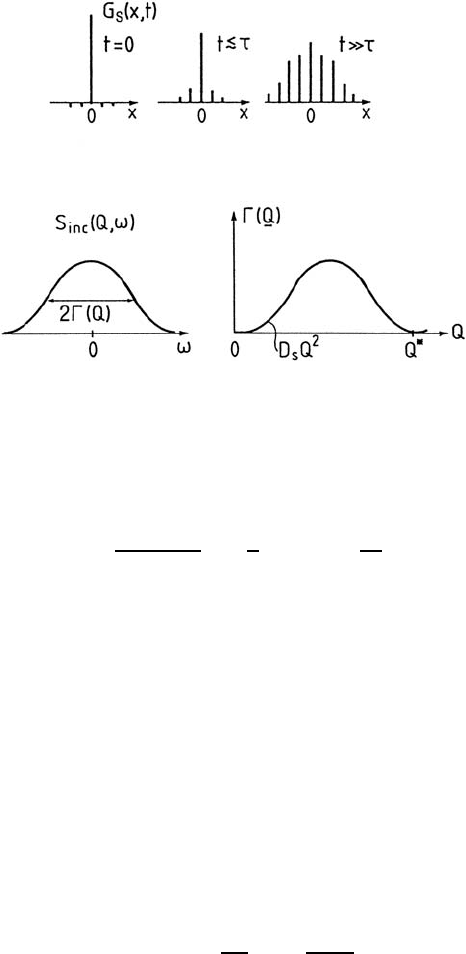
3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 103

Fig. 3.3. Top: G

(x, t) for a regular lattice. The height of the solid lines describes

the probability of occupancy per unit cell. Asymptotically, the envelope approaches

a Gaussian. τ is the mean rest time at a site.

Bottom: S

inc

(Q, ω) and quasielastic width Γ vs. scattering vector Q (schematic).

∗

is the reciprocal lattice vector for Γ =0andD

is the self-diﬀusion coeﬃcient.

∂P(r

,t)

∂t

= −

P (r

,t)+

sτ



ν=1

P (r

+ d

,t) . (3.25)

The ﬁrst and second term on the right side are the loss and growth rate

due to the jumps to and from adjacent sites, respectively. In order to obtain

(r,t) we impose the initial condition

P (r

, 0) = δ(r

) (3.26)

Because in a Bravais lattice all sites are equivalent, we directly obtain the

self-correlation function as the solution of the master equation: G

(r,t) ≡

P (r

,t) . The basic CE-model (represented by (3.25)) has been extended for

many special and more complex situations, for instance to include eﬀects due

to ion-ion correlations in ionic conductors; see (3.61) to (3.63) in Sect. 3.8. A

general theory of the master equation is given in Chap. 18. The approximation

 τ holds in most cases. For a H atom at room temperature one gets

∼

= d





1/2

∼

−13

s (3.27)

whereas normally τ ≥ 10

−12

s. Only in certain cases, e.g. for hydrogen in

vanadium at high temperatures, τ and τ

are comparable and the diﬀusion

coeﬃcient D

has values above 10

−9

/s, similar to diﬀusion coeﬃcients in

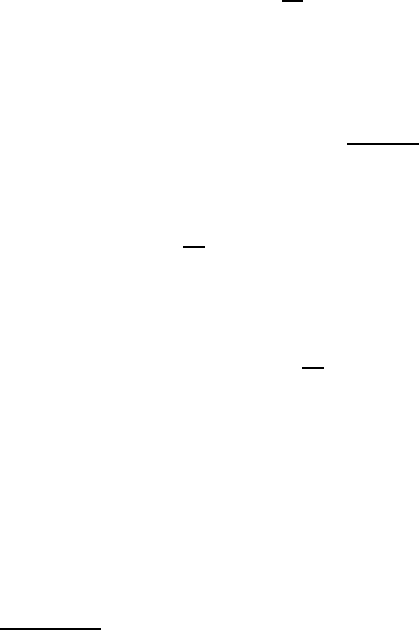
104 Tasso Springer and Ruep E. Lechner

liquids. Equation (3.25) further assumes that subsequent jumps are uncor-

related. Finally, blocking and mutual interaction eﬀects are neglected which

implies a low site occupancy c for the diﬀusing particles. One could improve

the calculation with respect to correlations between diﬀerent particles, re-

placing – as a meanﬁeld approximation – τ by τ/(1 −c), where (1 −c)isthe

blocking factor. Correlated jumps are discussed in Sects. 3.8 to 3.10, and in

Chaps. 1, 10, 18 and 21. Now we introduce the Fourier transform

P (r

,t)=



P (Q,t)e

−iQr

dQ, (3.28)

where

P (Q,t) ≡ I

(Q,t) from (3.7).

This leads to a diﬀerential equation of 1

order for

P (Q,t) whose solution

is an exponential decay function

P (Q,t)=e

−Γ (Q)t

, (3.29)

which fulﬁls the initial condition (3.14). From this one gets

Γ (Q)=

sτ



ν=1

(1 − e

−iQd

) . (3.30)

The resulting dynamic structure factor is the Fourier transform of

P (Q,t)=

(Q,t), namely a normalized Lorentzian

inc

(Q,ω)=

Γ/π

+ Γ

, (3.31)

with halfwidth Γ (Q). For a simple cubic Bravais lattice one gets the expres-

sion

Γ (Q)=

3τ

(3 − cos(Q

d) − cos(Q

d)) . (3.32)

x,y,z

are the components of Q.ForQ  1/d,whered is the length of the

jump vector, one gets the limiting case

Γ (Q)=

6τ

= D

. (3.33)

This relation holds generally and is independent of the detailed jump geom-

etry, except for “exotic” conditions (e.g. if the diﬀusion occurs in planes and

the jumps between neighbouring planes occur with a very small probability;

see Sect. 3.11).

Γ (Q) is periodic in reciprocal space. It has a maximum at the Brillouin

zone boundary and it is zero, if a reciprocal lattice point G is reached, such

that Γ (Q = G) = 0. This “line narrowing”

is related to Bragg diﬀraction of

the neutron wave from the probability density of the proton distributed over

the sites of the Bravais lattice. Obviously, the zero width at the reciprocal

This eﬀect should not be confused with the coherent line narrowing described in

Sect. 3.12.

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 105

lattice point is a consequence of the condition under which this theoretical

result has been obtained

, namely the assumption of inﬁnitely high energy

and momentum resolution and therefore inﬁnitely large observation time and

observation volume. In a real experiment, with ﬁnite resolution – just as in

coherent Bragg diﬀraction – the zero width cannot be directly observed. All

measured widths are ﬁnite, but for suﬃciently good resolution, the periodic

oscillatory behaviour of the diﬀusion linewidth due to this diﬀraction eﬀect

is nevertheless qualitatively retained. After correction for the eﬀects of reso-

lution, the theoretical line narrowing is indeed recovered (see below).

Let us consider a practical example. For instance, for a 1 µeV resolution

width (e.g. FWHM of a Lorentzian resolution function, corresponding to a

single exponential observation function) the observation time is as long as

0.66 · 10

−9

s. During this time a particle diﬀusing on an interstitial Bravais

lattice may thus be spread out over a regular arrangement of about 10

sites.

Consequently, during the same period the neutron wave packet is diﬀracted

on this extended “crystal-like” single-proton probability density distribution.

The time-evolution of the correlation function and the shape of the quasi-

elastic spectrum are shown schematically in Fig. 3.3.

As concerns the Fourier transform in Q the main contribution from the

integrand in (3.13) results from a range Qr

< 1 (contributions for larger Q

at ﬁxed r

cancel by rapid oscillations of the integrand, if G

is for instance a

Gaussian distribution with “radius” r

in space). Consequently, the volume

where G

is “observed” by a scattering experiment is about 1/Q

.Inpartic-

ular, measurements on diﬀusing atoms at small Q image the diﬀusion over

large distances and yield the self-diﬀusion coeﬃcient only, whereas the re-

sults for large Q values predominantly yield information on a single diﬀusive

step or on a few steps. The smallest Q values accessible in experiments are

of the order of 0.1

−1

. This implies that the scattering process “observes”

the diﬀusing ion in a volume of the order of (10

. For a diﬀusive process,

about z

∼

(Q)

−2

≈ 150 jumps come into play, if a jump length  of 2

is assumed. Consequently, the self-diﬀusion coeﬃcient from the quasielastic

width for small Q is a bulk quantity, and grain boundaries (see Chap. 8) will

not inﬂuence the result, in contrast to macroscopic methods.

There are of course more complicated situations than that described by

(3.25), for instance a bcc lattice with 6 non-equivalent interstitial lattices

which are interconnected. Here, the dynamic structure factor includes 6 eigen-

values and Lorentzians. For Q → 0 again a single Lorentzian remains with

Γ = Q

( [25], see Fig. 3.11). The complicated case of a non-cubic lattice

with a great number of inequivalent sites was treated for α-La

.In

this case [26], one calculates 9 eigenvalues. Part of them correspond to nearly

Theoretical models for neutron scattering functions are usually derived neglecting

experimental resolution; the latter is introduced a posteriori in the analysis of

the measured spectra.

106 Tasso Springer and Ruep E. Lechner

localized motions, which means that the corresponding quasielastic width is

almost independent of Q.

3.4 High Resolution Neutron Spectroscopy

In neutron scattering spectrometers, the wavelength, velocity or energy of

neutrons have to be deﬁned before scattering, and analyzed afterwards. Three

methods are being used: Crystal Bragg reﬂection (XTL), neutron time-of-

ﬂight (TOF), or neutron spin-echo (NSE). In the majority of quasielastic

neutron scattering experiments the scattering function, S(Q,ω), is measured

by TOF spectrometry with resolutions from about 1 µeV to a few 1000 µeV,

or by backscattering (BSC) spectroscopy, with resolutions of the order of

0.1 µeV to 1 µeV. This allows to cover, by quasielastic neutron scattering, a

range of diﬀusion coeﬃcients between 10

−12

/s and 10

−8

/s, or, corre-

spondingly, of characteristic times from 10

−9

sto10

−13

s. In certain cases,

also the NSE method can be used, which permits the direct determination of

the intermediate scattering function, I(Q,t), instead of S(Q,ω).Thistech-

nique extends the Fourier time scale up to 10

−7

s, corresponding to an energy

resolution limit in the neV region, where diﬀusion coeﬃcients of the order of

−13

/s can be measured. For detailed descriptions of the NSE-technique,

see [27] and Chap. 13. The TOF and BSC methods will be explained in the

following.There are diﬀerent techniques of neutron time-of-ﬂight spectrome-

try. XTL-TOF spectrometers [28] use a crystal monochromator to create a

continuous monochromatic beam. This is then periodically chopped with a

disk or Fermi chopper, before it hits the sample. The energy distribution of

the scattered neutrons is obtained by measuring their time-of-ﬂight from the

sample to the detectors. The latter should be suﬃciently thin, to make their

contribution to the ﬂight-time uncertainty negligible. The detectors cover a

large range of solid angle and of Q-values. This type of time-of-ﬂight instru-

ment (Fig. 3.4) is characterized essentially by four parameters: The incident

neutron wavelength λ

, its uncertainty ∆λ

, the pulse width ∆τ

,andthe

pulse repetition rate ν, typically several 100 Hz. While the wavelength uncer-

tainty is due to the divergence of the neutron beam incident on, and reﬂected

from the monochromator, the pulse width is deﬁned by the chopper; typical

values are ∆τ

=20to50µs. In Fig. 3.5 a neutron time-of-ﬂight diagram is

shown for a ﬂight path L (of the order of several meters) extending from the

sample to the detectors.

The pulse repetition rate is limited by the frame overlap, which means the

superposition of the fastest neutrons within a certain cycle and the neutrons

scattered with energy loss from the previous one (velocity v

min

). This requires

min

. (3.34)

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 107

Fig. 3.4. Typical time-of-ﬂight spectrometer with Bragg monochromator at the

FRJ-2 reactor. E

is selected by a Bragg monochromator crystal, E

by measuring

the ﬂight time.

rpm



Fig. 3.5. Time schedule for a time-of-ﬂight spectrometer. ∆τ

= pulse length, L =

ﬂight path after scattering, τ

rpm

= cycle length. ν =1/τ

rpm

= v

min

/L = repetition

rate. Shaded: frame overlap. v = v

corresponds to zero energy transfer ω =0.The

incident energy E

is selected by Bragg reﬂection from a monochromator crystal.

The choice of v

min

depends on the decay of the quasielastic spectrum on the

low-energy side. Obviously, the parameters ∆λ

, ν, and ∆τ

determine the

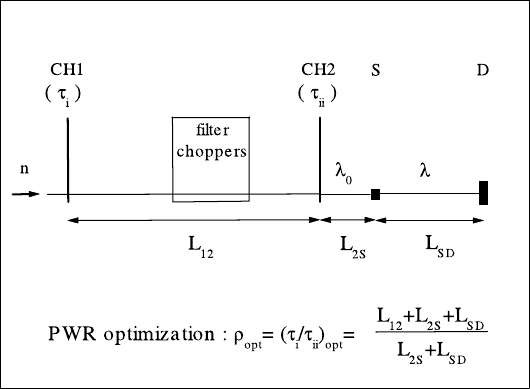
108 Tasso Springer and Ruep E. Lechner

Fig. 3.6. Schematic sketch of a multi-disk chopper time-of-ﬂight (MTOF) spec-

trometer: CH1 and CH2 are the two principal choppers deﬁning the monochromatic

neutron pulse and its wavelength bandwidth; S = sample, D = detectors; L

, L

and L

are the distances between these elements of the instrument; τ

and τ

are

the widths of the pulses created by CH1 and CH2, λ

, λ the incident and scattered

neutron wavelenths (after [29]). Inset: the pulse-width ratio (PWR) optimization

formula for elastic and quasielastic scattering [30]. Typical instruments of this type

are IN5 at ILL in Grenoble, MIBEMOL at LLB in Saclay, and NEAT at HMI in

Berlin.

average count rate at the detectors, while two of them, ∆λ

and ∆τ

,govern

the energy resolution.

As already mentioned, the incident neutron beam of the XTL-TOF spec-

trometer is monochromatized by Bragg reﬂection. It selects a certain wave

number k

= mv

/ for a given Bragg angle Θ and reciprocal lattice vector

G, following the Bragg equation

|G| =2k

sin Θ. (3.35)

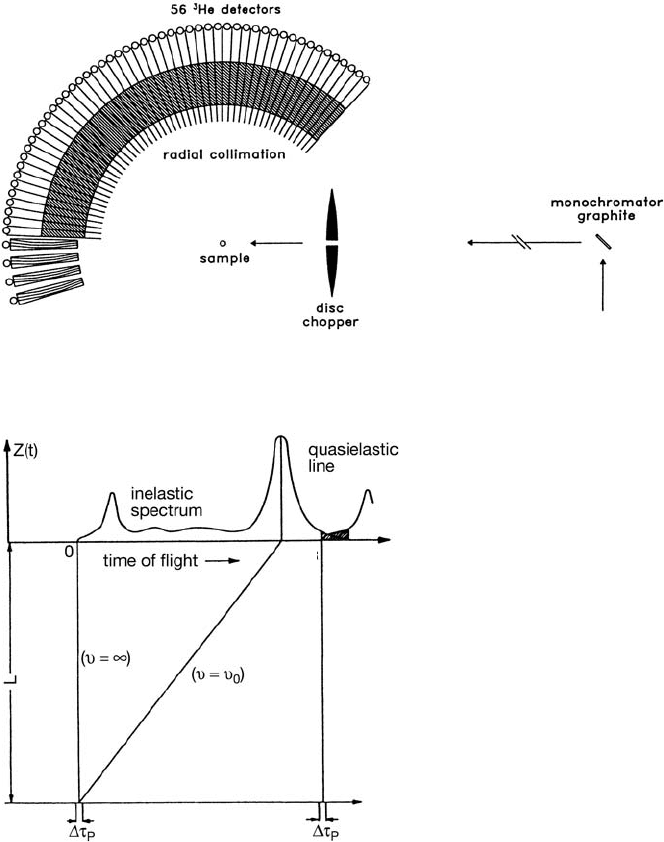
Alternatively, in the case of a TOF-TOF spectrometer, both v

and v

are

selected by time-of-ﬂight by (at least) two choppers in front of the sample,

with a mutual phase shift which determines v

. Such a multi-disk chopper

time-of-ﬂight (MTOF) instrument is illustrated in Fig. 3.6.

The two principal choppers, CH1 and CH2, the sample S and the detectors

D are separated by the distances L

, L

,andL

, respectively. CH1 and

CH2 create neutron pulses with widths τ

and τ

and deﬁne the incident

neutron wavelength λ

; the scattering processes cause neutron wavelength

shifts to smaller or larger values of λ.

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 109

For a given incident neutron wavelength, the total intensity at the detec-

tors is essentially governed by the factor (τ

), i.e. by the product of the

two chopper opening times [30] (see also: [31]). The latter also control the

resolution, and thus intensity and resolution are connected through these pa-

rameters. The most important and unique feature of this type of instrument

is the capability of varying the energy resolution continuously over several

orders of magnitude (see above). The energy resolution width (HWHM) at

the detector [30], i.e. the uncertainty in the experimentally determined energy

transfer ω,isgivenby

∆(ω)[µeV] = 647.2(A

+ B

+ C

)

1/2

/(L

)/2 , (3.36)

where

A = 252.78 ∆L λ L

, (3.37)

B = τ

+ L

/λ

) , (3.38)

C = τ

+ L

/λ

) . (3.39)

∆L is the uncertainty of the length of the neutron ﬂight path, which is mainly

due to beam divergence, sample geometry and detector thickness. The quan-

tities L

, L

, ∆L mustbegiveninm,λ

and λ in

Aandτ

, τ

in µs.

It follows from these expressions, that the energy dependent resolution, for

given λ

, strongly depends on the scattered neutron wavelength λ,whereas

the total intensity, as an integral property of the spectrometer, has no such

dependence. Furthermore, high resolution is favoured by short pulse widths

and by large values of the distances L

and L

. If these distances are

ﬁxed, and if sample geometry, λ

and energy transfer have been chosen,

then total intensity and resolution-width only depend on the chopper open-

ing times τ

and τ

. Best instrument performance regarding intensity and

resolution is achieved not only by selecting suitable values of the individual

pulse widths, τ

and τ

, but also requires the optimization of their ratio

(pulse-width ratio (PWR) optimization [30], [32]). The optimization formula

for elastic and quasielastic scattering is shown as an inset in Fig. 3.6.

The µeV-regime is covered by back scattering spectrometry [33–35], which

was invented by H. Maier-Leibnitz. BSC-spectrometers are XTL-XTL instru-

ments, i.e. they employ single-crystals as monochromators and as analyzers,

with Bragg angles close to π/2 in both cases. For a given incident divergence

of the beam, ∆Θ, the wave number spread produced by reﬂection from a

crystal is given by diﬀerentiating (3.35)

∆k

div

=cotΘ∆Θ . (3.40)

This relation is shown in Fig. 3.7 together with the presentation of the Bragg

law in reciprocal space. For typical Bragg angles and ∆k

div

/k ≈ 10

−2

radian

one achieves an energy resolution in the percent range. However, for Θ ap-

proaching π/2, ∆k

div

from (3.40) goes to zero and we have to include the

curvature of sin Θ which leads to a second order contribution (see Fig. 3.7)

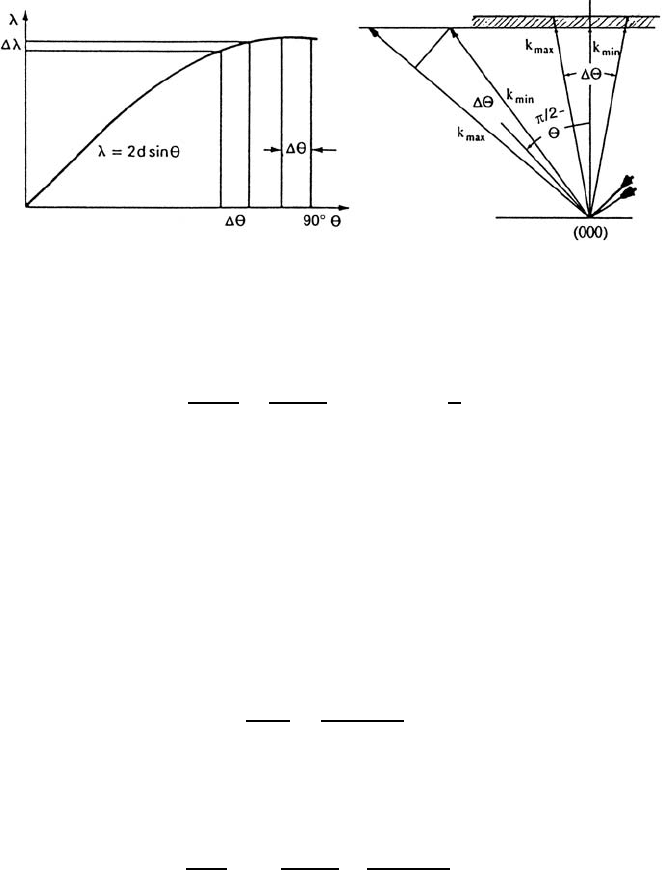
110 Tasso Springer and Ruep E. Lechner

Fig. 3.7. Bragg law and Bragg reﬂection on a single crystal monochromator in

reciprocal space, for Θ

oﬀ 90

◦

,andforΘ

≈ 90

◦

where k depends only in 2

order on ∆Θ. Vertical line: G = reciprocal lattice vector. Width of shaded region:

Darwin width due to extinction.

∆k

div

(∆Θ)

for Θ →

. (3.41)

This situation is called “backscattering” which means that the incident and

the Bragg reﬂected beam are practically antiparallel. The square relation

(3.41 replaces the linear relation between ∆k

div

and ∆Θ: The intensity is

proportional to the incident solid angle (∆Θ)

, and we have (∆Θ)

∝ ∆k

div

instead of ∆Θ ∝ ∆k

div

, which is valid for Bragg angles other than π/2. This

means that under these conditions resolution and intensity are decoupled in

ﬁrst order.

Actually, the wavevector spread is larger than ∆k

div

. Only a ﬁnite number

of lattice planes contributes to the Bragg line, which causes a ﬁnite width of

G, the so-called Darwin or extinction width [36], namely

∆k

16πN

, (3.42)

where F

is the structure factor for the Bragg reﬂection at Q = G, N

is the number of lattice cells per unit volume. As an approximation, both

contributions can be added such that

∆E



(∆Θ)

16πN



. (3.43)

For neutrons from a Ni neutron guide and reﬂection on an ideal silicon waver

one calculates ∆E

=(0.24+0.08) µeV. For the resolution in energy transfer,

∆(ω), of a modern BSC-spectrometer, one obtains values between 0.09 µeV

and 0.43 µeV (HWHM), depending on the type of crystals used [35]. So far

such values have not been reached by any other crystal spectrometer; they

will, however, be achieved also by high-resolution TOF-TOF instruments at

future spallation sources [29]. The Bragg angle is ﬁxed at 90

◦

, and the energy