Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

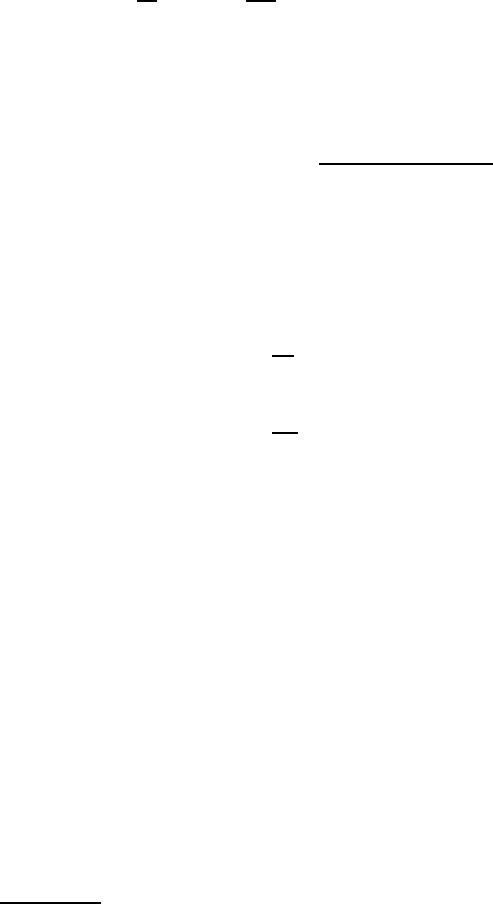
70 Gero Vogl and Bogdan Sepiol

We restrict the discussion to the simple case of Markov processes. This

leads to a Markov master equation (see Chaps. 3 and 18) [15], which is a

linear diﬀerential equation (rate equation) for the evolution of the probability

density P (r,t) to ﬁnd an atom at site r at time t

∂

∂t

P (r,t)=

Nτ



i=1

{P (r + r

,t) − P (r,t)} . (2.2)

With respect to some boundary conditions the solutions of this equation give

the self-correlation function G

(r,t). The shape of the resulting S(Q,ω)(see

(2.1)) is a Lorentzian

S(Q,ω) ∝ f

Γ (Q)/2

(Γ (Q))/2)

+(ω)

(2.3)

where f

is the above mentioned Debye-Waller factor (lattice vibrations)

and Γ (Q) is the full width at half maximum (in the following denoted as

“(diﬀusional) line broadening”) of the Lorentzian. Γ (Q) depends on Q · r

and hence on the relative orientation between radiation and crystal:

Γ (Q)=

2

⎡

⎣

1 −



⎤

⎦



i=1

iQ·r

. (2.4)

Here τ

−1

is the jump rate (τ is the mean residence time of an atom between

two successive jumps), W

is the probability

for a jump to coordination shell

j and E

the corresponding structure factor. N

denotes the number of sites

in coordination shell j and the r

are the i =1...N

jump vectors to sites

in shell j.

Non-Bravais Lattices

Some alloys do not form a “simple” solid solution, i.e. a Bravais lattice with

sites statistically occupied by atoms of the alloy constituents, but exhibit

an additional type of order: they form a superlattice made up of diﬀerent

sublattices each of which belongs to one species of atoms. Because in the

stoichiometry they are well ordered, a degree of order can be well controlled

by temperature, chemical composition and, beyond that, they are of high

technological interest [16]. Such lattices contain more than one atom per

primitive unit cell depending on the type of superstructure. It is energeti-

cally disfavoured to place an atom of a given species at a site on a “wrong”

Note that the W

are normalized, i.e. the sum over all W

equals unity.

2 Diﬀusion Studied by Interference of γ-Rays, X-Rays and Neutrons 71

sublattice (antistructure defects). This complicates the diﬀusion mechanisms,

as e.g. jumps of a given atom species leading to wrong sites may be markedly

less probable than jumps to sites on the own sublattice, i.e. there are diﬀerent

jump rates. In this case it is not suﬃcient to set up only one Markov equation

as in Sect. 2.2.1 for Bravais phases. For a superstructure with m sublattices

one needs m Markov equations. To solve such a system of m coupled rate

equations a matrix formalism is used. The Chudley and Elliott theory [8] was

extended by Rowe et al. [17] for hydrogen diﬀusion on interstitial sites of a

non-Bravais lattice. The Rowe theory assumes equal occupation of diﬀerent

sublattices (sites with diﬀerent “local symmetry” in the unit cell), and at-

tempts to extend the theory for systems with diﬀerently occupied sublattices

have been undertaken [18, 19]. This problem has been treated in details by

Randl et al. [20] for non-Bravais structures.

The jump matrix containing the coeﬃcients of the Markov equation is in

general not Hermitian but has always real eigenvalues and thus can be trans-

formed to a Hermitian matrix [18]. Diagonalization of the hermitized jump

matrix gives the solutions of the Markov equations. The spectra of an alloy

with m sublattices are made up from m Lorentzian lines

. The linewidths of

the subspectra are calculated from the eigenvalues and the relative contribu-

tion (weight) of each subspectrum is determined by the eigenvectors.

The jump rates between nearest neighbour (NN) sites are constrained by

the detailed balance which demands that the number of atoms jumping in a

time unit from one sublattice into another must be equal to the number of

reverse jumps

(2.5)

where c

is the probability of occupation of the ith sublattice and



=1.

1/τ

is the jump rate from a site of symmetry i to any of n

nearest-neighbour

sites.

We treat the so-called B2 structure (see Sect. 1.10 in Chap. 1) as an ex-

ample. This superstructure of two-component alloys AB is of special interest

for diﬀusion studies because in a B2 lattice each atom is surrounded by lattice

sites, which belong to the other species. It is based on a bcc unit cell where

atoms of one species occupy the edges of the unit cell while the body centred

positions belong to atoms of the other species. Thus NN jumps lead always to

antistructure sites. If such NN jumps are the only operative diﬀusion mech-

anism, we have to set up a 2 × 2 jump matrix and arrive at spectra which

are a sum of two Lorentzians. A useful quantity is the asymmetry parameter

α = τ

/τ

(where τ

is the mean residence time of diﬀusing atoms on their

own sublattice 1 and τ

analogous for the wrong sublattice 2)

A sum of Lorentzians is – in general – not a Lorentzian.

Note that the same number of A atoms per unit time must jump from sublattice

1 to sublattice 2 and vice versa (“detailed balance”). Thus α is directly connected

to the occupation of the sublattices via α = τ

/τ

= c

72 Gero Vogl and Bogdan Sepiol

Fig. 2.3. B2 Structure: broadening and relative contributions (weights) of the two

quasielastic M¨oßbauer lines as a function of orientation ϑ for diﬀerent values of the

asymmetry parameter α.

This parameter rules the shape of the spectra because the two residence

times τ

and τ

(or – in turn – the two jump rates τ

−1

and τ

−1

)are“respon-

sible” for the diﬀusional line broadening of the two subspectra and their re-

spective contribution to the sum spectrum. Figure 2.3 shows the orientation-

dependent part of the line broadenings of the two subspectra (upper row)

and their contributions (lower row) for three diﬀerent values of α.Forawell

ordered B2 alloy AB the mean residence time τ

of atoms of species A on

their own sublattice 1 is much longer than the mean residence time τ

on the

“wrong” sublattice 2, which belongs to the other species B (as the total con-

centration of antistructure defects is low). Therefore α has a large value and

for large α one of the two Lorentzians is very broad while the other is rather

narrow (upper row in Fig. 2.3). But in turn the contribution of the broad line

is small (lower row). This leads to an experimental diﬃculty: such a broad

but weak line can hardly be observed because it vanishes in the background

of the measured spectra. The spectra seem to consist of one Lorentzian. This

holds even for an alloy, which already contains some excess iron atoms (e.g.

with α =7.0, see Sect. 2.3.2).

The less well-ordered a B2 alloy is, i.e. the more antistructure defects a

B2 alloy contains, the more α decreases. For a moderate value of α like, e.g.,

α =2.45 the broad line is not “too broad” and the relative contribution of

the broad line is higher (in some directions even higher than the contribution

of the narrow one). In such a case the two lines are easily resolvable, e.g., in

[113] direction. If α equals unity – i.e. the two residence times are equal –

in any direction one of the two lines vanishes. The resulting line broadening

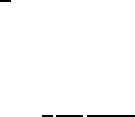
2 Diﬀusion Studied by Interference of γ-Rays, X-Rays and Neutrons 73

of the remaining single line is essentially the same as for diﬀusion in a bcc

Bravais lattice.

If the jump mechanism and jump rates are known one can calculate the

macroscopic diﬀusion coeﬃcient, which can be compared with the tracer dif-

fusion coeﬃcient. The diﬀusion coeﬃcient is in a non-Bravais lattice a sum

of partial diﬀusion coeﬃcients [4], where 1/τ

is the jump rate from a site of

symmetry i to any nearest-neighbour site of symmetry j

D =



i,j

− r

)

−1

. (2.6)

Applying (2.6) to the B2 lattice structure one obtains

D =

α +1

, (2.7)

where a is the lattice constant. QEMS diﬀusion coeﬃcients [21,22], measured

without assuming any correlation eﬀects, coincide well with tracer diﬀusion

values [23–25]. This is an argument against highly correlated diﬀusion mech-

anisms in B2 alloys (see Sect. 2.3.2).

2.2.2 Nuclear Resonant Scattering of Synchrotron Radiation

Nuclear resonant scattering of synchrotron radiation (NRS) was applied for

diﬀusion studies in the middle nineties [26]. Immediately after the theoretical

paper of Smirnov and Kohn [27] the ﬁrst feasibility study has been performed

at ESRF Grenoble [26].The most important diﬀerence between NRS and the

quasielastic methods QEMS and QENS is that NRS works in the time domain

whereas the quasielastic methods work in the energy domain. The principal

idea of NRS is: the coherence of the synchrotron radiation (SR) in the forward

direction, after nuclear resonance absorption in the sample, is destroyed by

diﬀusion, which leads to a faster decay of the scattered intensity in forward

direction with respect to an undisturbed process. From this “diﬀusionally

accelerated” decay, details on the diﬀusion process can be derived.

The mathematical formulation of the problem can be found in [28–30].

Here we give only an outline characterizing diﬀerences between NRS and

QEMS/QENS.

In QEMS and QENS techniques the experimental spectrum S(Q,ω)is

obtained in the energy domain. In order to be compared with the mi-

croscopic diﬀusion mechanism described by the theory through the self-

correlation function G

(r,t), it must be double Fourier transformed (see

(2.1)) S(Q,ω) ↔ I(Q,t) ↔ G

(r,t), where the intermediate scattering func-

tion I(Q,t) is the result of the ﬁrst (space-momentum) Fourier transform.

For simple Markovian diﬀusion on a crystalline Bravais lattice, the interme-

diate scattering function in forward direction, I

(Q,t) can be calculated

analytically yielding the following exponential time-dependent function

74 Gero Vogl and Bogdan Sepiol

(Q,t) ≈ I

4τ

exp



−



(Γ

+ Γ (Q))



, (2.8)

where L is the eﬀective sample thickness proportional to the Debye-Waller

factor, I

the scattered intensity at time zero and Γ (Q) is the linewidth

of (2.4). Equation (2.8) shows that the logarithm of the decay rate is pro-

portional to the width of the diﬀusional broadening Γ (Q)asmeasuredin

classical QEMS. Equation (2.8) is correct only in the thin-sample approxi-

mation due to the much more important role of the eﬀective sample thickness

in NRS than in QEMS or QENS. The most important isotope, which can be

used for diﬀusion studies by NRS, is once again

. In Fig. 2.4 the ef-

fect of increasing temperature resulting in the faster decay of the scattered

intensity in forward direction is clearly visible. At lower temperatures an ef-

fect of increased eﬀective sample thickness L results in the curvature of the

exponential. If the sample is enriched in

Fe isotope one can obtain very

high count-rates and much shorter measuring times compared to quasielastic

methods from Sect. 2.2.1.

2.2.3 Neutron Spin-Echo Spectroscopy

Neutron spin-echo (NSE) spectroscopy [31] has been successfully applied to

the study of the dynamics in amorphous systems (proteins, polymers, glassy

dynamics etc.) but we have shown that it is also suited for the investigation

of diﬀusion on lattices giving direct access to the jump mechanism [32].

NSE is a Fourier method and is sensitive to the time-dependent correlation

function yielding directly the intermediate scattering function I(Q,t)(see

preceding section). It bridges the gap in time scale between conventional

quasielastic neutron scattering and dynamic light scattering. NSE combines

the high energy resolution from QENS with the high intensity of a beam

which is only moderately monochromatic. In NSE the velocity change of

neutrons after scattering by a sample is measured by comparing the Larmor

precession in known magnetic ﬁelds before and after the scattering. This

comparison is made for each neutron individually, thus the resolution of the

velocity change can be much better than that corresponding to the width

of the incident beam. A detailed explanation of the method can be found in

Chap. 13.

To demonstrate the potential of the method to observe directly the jump

of atoms, NiGa as a model system was used (see ﬁgures in Sect. 2.3.2). An

unambiguous decision between two opposed diﬀusion models can be obtained

on the basis of two spectra only, provided the measurement is performed at Q

values near reciprocal superlattice points. From the experimental resolution

one can conclude, that diﬀusivities are around 10

−13

−1

NRS may be called M¨oßbauer spectroscopy in the time domain.

2 Diﬀusion Studied by Interference of γ-Rays, X-Rays and Neutrons 75

Fig. 2.4. Time dependence of

forward scattered intensity at

three temperatures with the

beam parallel to the crystal di-

rection [110] of a stoichiometric

FeAl sample.

2.2.4 Non-Resonant Methods

In the following a very basic approach for the calculation of the structure fac-

tor will be presented. Description of atomic movements by the self-correlation

function G

(r,t) is actually only a special case of the more general descrip-

tion by the pair correlation function G(r,t). An expression for the coherent

scattering function on Bravais lattices has been given by Ross and Wilson [33]

(this problem is also discussed in Chap. 3 and in [34]).

One can split the pair-correlation function into a time-dependent part



(r,t) and a static part: G(r,t)=G



(r,t)+cΣδ(r − r

) [35], where c is

the concentration of the scattering atoms on the Bravais lattice, r

is the ith

lattice site and the summation is over all lattice sites. Inserting this equation

into (2.2) and solving by Fourier transformation with the boundary condition

G(r, 0) = (1 − c)δ(r)+cΣδ(r − r

) the coherent scattering function reads

S(Q,ω)=c(1 − c)

Γ (Q)



Γ (Q)



− (ω)

+ cNδ(ω)δ(Q − G) . (2.9)

76 Gero Vogl and Bogdan Sepiol

Equation (2.9) describes coherent scattering on Bravais lattices [34, 35]. The

quasielastic term with Lorentzian lineshape is, apart from a factor c(1 − c),

identical with the scattering function calculated from the self-correlation

function G

(r,t) for incoherent scattering (2.3). The purely elastic term de-

scribes Bragg scattering in directions, where the scattering vector equals the

reciprocal lattice vector G. The quasielastic term describes isotropic diﬀuse

scattering (note the pre-factor c(1−c) characteristic for the Laue-diﬀuse scat-

tering [36]). Note, that (2.9) is derived for a lattice occupied by one type of

scattering atoms only. Derivation for the case of a non-Bravais lattice with

one or more scattering atoms was achieved for the ﬁrst time by Kaisermayr et

al. [35,37]. General conclusions are similar to conclusions in a Bravais lattice;

no quasielastic broadening apart from a negligible contribution from diﬀuse

scattering, can be expected in the Bragg reﬂections, irrespective if they are

of fundamental or superstructure type. If the lattice is occupied by more

than one scattering element, the diﬀerent quasielastic parts are obtained by

simple summation of all elementary contributions. This prediction was exper-

imentally proven by measuring diﬀusion in B2 Co

using time-domain

interferometry of synchrotron radiation [37]. For the idea of the method we

refer to Baron et al. [38].

From (2.9) and from equivalent derivation for non-Bravais lattices [35,37]

the following conclusions can be drawn:

– The coherent scattering function for diﬀusion in crystal structures is elas-

tic in Bragg reﬂections of fundamental and superstructure peaks.

– In the regions between the reciprocal lattice points, the quasielastic diﬀuse

scattering can be observed, i.e. scattering due to lattice disorder (Laue-

diﬀuse scattering). The scattering function S(Q,ω)iscalculatedinthe

same way as the scattering function for the incoherent scattering, i.e., is

calculated from the self-correlation function (2.1).

– The largest intensity of the quasielastic component is in superstructure

lattice directions of the non-Bravais lattice

. It is not possible, however,

to measure quasielastic broadening at these positions since the diﬀuse

intensity will be completely hidden under the elastic Bragg line.

Observation of the diﬀuse scattering is diﬃcult due to the very low inten-

sities, thus large detectors are necessary. Higher intensities can be measured

by scattering on samples without lattice structure, e.g. on glassy samples.

Such a glassy sample was measured by synchrotron radiation in the ﬁrst

time-domain interferometry experiment of Baron et al. [38], or by Rayleigh

scattering of M¨oßbauer γ-quanta [39].

Finally a most interesting development should be mentioned: a new

method in diﬀusion studies is the X-ray photon correlation spectroscopy

For instance in the ordered B2 structure the largest intensity is in the [100]

direction.

2 Diﬀusion Studied by Interference of γ-Rays, X-Rays and Neutrons 77

(XPCS), which is a version of the old laser-speckles spectroscopy, but with

X-rays that can be used for the studies of metallic systems [40]. Although

in the best current third-generation X-ray sources the degree of coherence is

much lower than for lasers in the visible range, it is still suﬃcient for studies

of nanometer-size objects like studies of the dynamics of coarsening processes

or the motion of antiphase boundaries.

Preliminary results of time-domain interferometry, Rayleigh scattering of

M¨oßbauer radiation or XPCS, which are all non-resonant methods, i.e. not

limited to studies of selected isotopes only, are very promising. They predict

new possibilities for diﬀusion studies of atomistic processes. Though bril-

liance of current synchrotron radiation sources is insuﬃcient for the studies

of atomic motion in crystalline solids, future sources like free electron lasers

will deﬁnitely enable this kind of research.

2.3 Experimental Results

2.3.1 Pure Metals and Dilute Alloys

Self-Diﬀusion in β-Titanium

Self-diﬀusion in titanium belongs to the fastest self-diﬀusion processes in

metals. The interesting question of the underlying mechanism was solved by

the use of QENS [41] and phonon spectroscopy [42] (see also Chap. 3 of this

book).

The driving force for diﬀusion jumps in metals are phonons. With the help

of phonon spectroscopy the reason for the high diﬀusivity in titanium could

be found [42]. At elevated temperatures the phonon spectrum of titanium

contains some very soft phonon modes, which inﬂuence the diﬀusion process.

Soft phonons correspond to large vibration amplitudes in real space. Parts of

the experimentally found atomic periodic displacements are parallel to the

direction of NN diﬀusion jumps while others periodically open and close the

conﬁgurational “windows” made up from other atoms through which an atom

has to pass in order to change the site. Therefore the atoms are “pushed”

to vacant NN sites and the migration energy is considerably lowered. This

explains the high diﬀusivity in titanium. Of course – for other metals or alloys

– other reasons for fast diﬀusion are possible. One of these will be discussed

for the case of Fe

Si in Sect. 2.3.2.

Iron Diﬀusion in Aluminium and Copper

Diﬀusion of dilute

Fe in f.c.c Al or Cu single crystals has been investigated

by QEMS ( [43] and [44]). As this is not self-diﬀusion but impurity diﬀusion

one needs a somewhat extended theory, which was elaborated by Le Claire

[45] and Krivoglaz and Repetskiy [46] (see also Sect. 1.9) and adapted to the

78 Gero Vogl and Bogdan Sepiol

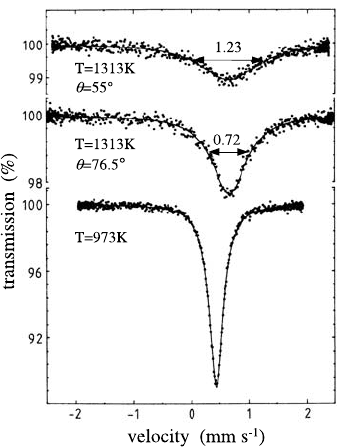
Fig. 2.5. QEMS spectra of dilute

Fe in copper single crystals. No-

tice that the linewidth of the spec-

tra measured at 1313 K is diﬀerent

for diﬀerent directions of observation

ϑ =55

◦

and ϑ =76.5

◦

current cases in [43] and [44]. This theory accounts for the fact that vacancies

are preferentially situated near the impurity atoms.

Figure 2.5 shows, as an example, four spectra measured on iron-doped

copper single crystals at 973 K (bottom) and at 1313 K at three diﬀerent

orientations. The ﬁtted single Lorentzian lines at 1313 K are not only broader

than at 973 K but also show a variation of the linewidth with orientation

ϑ (which is the angle between the M¨oßbauer wave vector Q and the [001]

crystal axis). In both metals the basic impurity diﬀusion mechanism could be

identiﬁed as a jump of an impurity atom to a nearest neighbour vacancy. The

diﬀusion coeﬃcients determined for iron in copper at various temperatures

agree well with reference data [47] obtained by the tracer diﬀusion method.

2.3.2 Ordered Alloys

B2 Structure (CsCl Structure)

Iron Diﬀusion in FeAl

Within a wide homogeneity range on the iron rich side Fe

1−x

alloys crys-

tallise in the B2 structure. As pointed out in Sect. 2.2.1, NN jumps in B2

lattices always lead to antistructure sites and should therefore be energeti-

cally disfavoured. Of course, this is only valid near equiatomic stoichiometry.

In alloys with more than 50 at.% Fe the excess iron atoms are situated on

aluminium sites, i.e. they form “built-in” antistructure defects.

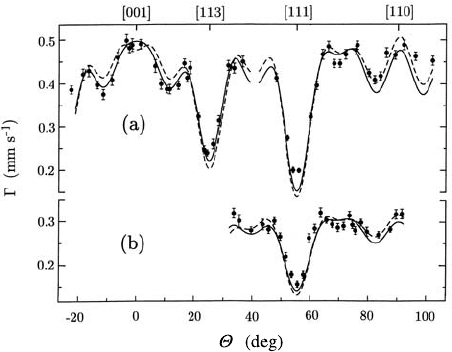
2 Diﬀusion Studied by Interference of γ-Rays, X-Rays and Neutrons 79

Fig. 2.6. Diﬀusional line broadening in Fe

50.5

49.5

(a) at 1065

◦

C for two diﬀerently

oriented slices (1 and 2) of the same crystal and (b) at 1040

◦

C for slice 1.

The most intriguing question for well ordered FeAl is, whether diﬀusing

atoms overcome the ordering energy and jump to NN sites or whether they

perform “far” jumps to e.g., second or third neighbour sites, which belong

to their own sublattice. Secondly, if a vacancy diﬀuses randomly via NN

jumps in a B2 lattice, it leaves a trace of antistructure defects behind. Thus

random diﬀusion of vacancies via NN jumps destroys the B2 superstructure.

In order to conserve the superstructure, vacancy diﬀusion via NN jumps

requires mechanisms, which restore the order after disordering jumps. Some of

the proposed mechanisms, which fulﬁl this condition, are discussed in Chap. 1.

Measurements on well-ordered Fe

50.5

49.5

[21] show, that all spectra are

well ﬁtted by single Lorentzian lines. At ﬁrst glance it follows from this that

iron diﬀusion occurs on a Bravais lattice, i.e. via “far” jumps between sites on

the iron sublattice and not via NN jumps to aluminium sites. If we plot the

line broadening (Γ

already subtracted) as a function of orientation we obtain

Fig. 2.6. These data can be ﬁtted with a superposition of the functions corre-

sponding to [100]- and [110]-jumps (solid line). A similar good ﬁt is obtained

with an additional 10% contribution of [111]-jumps (broken line). Further

measurements on the oﬀ-stoichiometric alloy Fe

[22] give similar re-

sults, but in this case the data can not be ﬁtted without a 20% contribution

of [111] jumps. Note that jumps directly to a [111] site, i.e. across the body

diagonal of the B2 unit cell, are hardly possible unless the body-centered

aluminium site is vacant.

Measurements of nearly-stoichiometric FeAl have been repeated with the

NRS method yielding a combination of [100] and [110] jumps in the ratio