Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 131

Φ(ω)=Φ



+iΦ



=1+

∞



W (t



iωt



. (3.62)

With this relation one derives a generalized Nernst-Einstein equation with

correlations, where the conductivity σ is replaced by the complex function

˜σ(ω)/Φ(ω) [89]. These relations lead to a modiﬁed Chudley-Elliott formula

which now reads

inc

(Q, ω)=



/π



+[ω + Γ



]

, (3.63)

where Γ

is the width as deﬁned in (3.30). Obviously, for Φ = Φ



=1and



= 0 the conventional Chudley-Elliott result is recovered. A very accurate

shape analysis of the quasielastic line, taking the complex conductivity ˜σ

and Φ from impedance spectroscopy, could demonstrate the validity of this

concept and may contribute to the understanding of the conductivity in terms

of correlated back jumps. Attempts with this goal were published for RbAg

[90]. The key problem is the accurate shape analysis and also the careful

elimination of coherent scattering contributions in such crystals.

3.9 Proton Diﬀusion in Solid-State Protonic Conductors

The speciﬁc dynamical features which generally distinguish protonic from

other ionic conductors, are connected with the fact, that hydrogen bonding

plays an important role. In particular, it is the process of formation and

breaking of H-bonds, which represents an important ingredient of the diﬀu-

sion mechanisms in these materials. Although the details of such mechanisms

may be quite complex, there are four basic types which have been discussed

in the literature [91]. They all take account of the fact that the proton is - at

least temporarily - bonded to an acceptor atom or molecular subunit.

(i) Grotthuß Mechanism

The original idea of Grotthuß (1806) which had dealt with electrical

charge transport along chains of water dipoles in liquid water, has been

transformed through extensive work during the 20th century [92–95] to a de-

scription valid for proton transfer within extended H-bonding networks [96]

in solids. The essential ingredients of this mechanism are alternating trans-

lational and rotational steps of the proton motion. In a translational step

the proton is exchanged via a hydrogen bridge between diﬀerent molecular

units. Subsequently the proton is transferred into another H-bond by a re-

orientational motion of the acceptor molecule, whereby the latter remains

ﬁxed to its site in the crystal lattice. The repeated occurrence of these alter-

nating processes leads to the uninterrupted trajectory of proton migration

inherent in translational diﬀusion. The Grotthuß mechanism is of impor-

tance for instance in certain solid alkali metal hydroxide hydrates, such as

132 Tasso Springer and Ruep E. Lechner

CsOH·H

O [97] (see below), crystalline framework hydrates [98], solid acidic

salts [99], and in many other materials.

(ii) Simple Molecular Diﬀusion Mechanism

When the proton is part of a stable mobile ion in a liquid, for instance of

the (NH

)

ion in liquid ammonium salts, it is simply transported through

the material by translational diﬀusion of the ion, whereby this charge carrier

is also performing a diﬀusive rotational motion. But there is no transfer of

protons between diﬀerent carriers. This mechanism appears to be relevant

not only in molecular liquids, but also for the high-temperature superionic

conducting regimes of the quasi-liquid layers in solid (NH

)

and (H

β-aluminas [100–103].

(iii) Vehicle Mechanism

This name has been given to the mechanism in systems, where - as in the

case of molecular diﬀusion - the proton is not migrating as the bare hydrogen

ion H

, but in a bound state, attached to a vehicle such as for instance H

forming (H

)orNH

forming (NH

)

. In contrast to simple molecular

diﬀusion, however, the neutral vehicles participate in a cooperative motion

together with the charged vehicles, for instance, by changing place with their

partners (counter-diﬀusion). The vehicle mechanism has been proposed, e.g.,

for concentrated aqueous solutions of acids [104] and for acidic solid hydrates

[105,106].

(iv) Mixed Mechanism

This mechanism combines essential ingredients of the Grotthuß mech-

anism (orientational rearrangement of neighbouring charged and uncharged

units with respect to each other, and proton transfer via H-bonds) with those

of the vehicle mechanism (inter-diﬀusion of charged and uncharged particles).

The lifetime of the vehicle-proton complex is ﬁnite, as compared to the time

constant of translational diﬀusion. This situation has been found to exist in

diluted aqueous solutions of acids and bases [104] and in certain acidic solid

hydrates with high water content [107]. Note that the mixed mechanism may

be considered as the Grotthuß mechanism of liquids and lattice liquids, since

it diﬀers from the mechanism (i) mainly by the fact that its vehicles are not

ﬁxed to lattice sites.

The interest in comparing Grotthuß, vehicle and mixed mechanisms to

the simple molecular diﬀusion model mentioned above, resides in the fact

that the latter allows a very simple theoretical derivation of the incoherent

neutron scattering function, S

inc

(Q,ω), which - under certain conditions -

is also applicable to the former mechanisms. This will be outlined in the

following.

In a molecular liquid or in quasi-liquid two-dimensional systems (e.g.

certain liquid crystalline phases or quasi-liquid layers of intercalation com-

pounds) molecules are performing a diﬀusive rotational motion, while they

are migrating through the bulk of the material by some random-walk long-

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 133

range translational diﬀusion process. At any given instant, the molecule is

sitting in a (possibly transient) local potential well, where it is taking part in

the external and internal molecular vibrations characterizing the system. The

calculation is greatly facilitated, if vibrational, rotational and translational

motions are assumed to be (dynamically) independent. This convolution ap-

proximation allows us to write (see [14, 15])

inc

(Q,ω)=S

vib

(Q,ω) ⊗ S

rot

(Q,ω) ⊗ S

trans

(Q,ω) . (3.64)

Here, S

vib

(Q,ω),S

rot

(Q,ω),S

trans

(Q,ω) are the incoherent scattering func-

tions of the three individual types of motions, and the symbol ⊗ stands for

the convolution in energy transfer  ω. The question, why this convolution

approximation can be applied, for instance, to the Grotthuß mechanism, re-

quires some discussion. The vibrational term in this convolution can usually

be replaced by a Debye-Waller factor, as long as the study is restricted to

the quasielastic region. Strictly speaking, the independence approximation

of rotational and translational motions is invalid, since the two motions are

not occurring simultaneously and independently of each other, but as a se-

quence of alternating steps. The validity of the approximation is however

recovered, if the rate of rotational steps, H

rot

, is much higher than the rate

of translational steps, H

trans

, because then it can be argued that the proton is

quasi-continuously participating in the rotational motion. This has been the

justiﬁcation for applying the molecular diﬀusion model for a number of su-

perprotonic conductors exhibiting the Grotthuß mechanism [97,99,108]. The

vehicle and mixed mechanisms can also be treated with the same method,

if diﬀerences in the parameters of charged and uncharged vehicles are taken

into account.

Now let us consider the application of this approximation to the Grot-

thuß case. Under the condition that the rates diﬀer by at least one or-

der of magnitude (a situation typical for many protonic conductors), one

can study the rotational motion “alone” in a low or medium resolution ex-

periment by choosing an intermediate energy resolution ∆(ω) such that

H

trans

 ∆(ω) ≤ H

rot

. This simply means that the experimental obser-

vation time ∆t (which in practice cannot be made inﬁnite; see the related

discussion in Sect. 3.2) is larger than the build-up time of the local PDD (for

instance due to a reorientational motion), but much smaller than its time

of decay due to long-range diﬀusion. The EISF of the rotational motion can

then be determined from the integral of the only weakly broadened elastic

peak, whereas the rotation rate is obtained from the quasielastic line width

of the broader spectral component. Vice versa translational diﬀusion is stud-

ied alone in a high-resolution experiment with ∆(ω) ≤ H

trans

 H

rot

because under this condition the rotational component will contribute only

a ﬂat background to the spectrum, whereas the diﬀusion parameters can

be determined from the Q-dependent linewidth of the central component of

inc

(Q,ω).

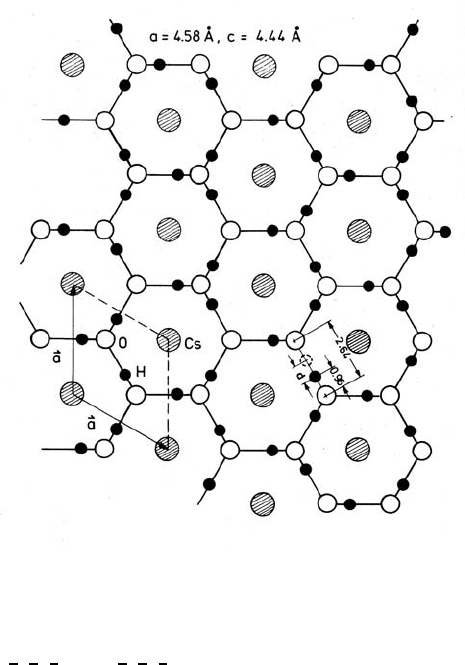
134 Tasso Springer and Ruep E. Lechner

Fig. 3.22. Trigonal modiﬁcation (T>340 K) of the solid-state protonic conductor

CsOH ·H

O: Projection onto the a-a plane, assuming a random distribution of the

hydrogen atoms between the oxygen atoms, with an O-H bond length of 0.96

The Cs atoms are located at the corners of the unit cell, the O atoms are placed at

(

)and(

); (after [109]).

This concept has been applied by Lechner et al. [97] to the analysis of

quasielastic neutron scattering data of the quasi two-dimensional solid-state

protonic conductor CsOH ·H

O. The crystal has a trigonal structure consist-

ing of pseudo-hexagonal planar [H

O − OH]

−

networks sandwiched between

and alternating with Cs

-ion layers (Fig. 3.22). Protons are transported

through the crystal lattice by a combination of translational motion across

the H-bond connecting adjacent H

OandOH

−

groups, and reorientation

of the latter. At 402 K, for medium energy resolution, this material exhibits

a two-component spectrum. The Q-dependence of the relative elastic inten-

sity (EISF; see Sect. 3.2) was shown to be consistent with the assumption

of OH

−

reorientations acting as mediators in the much slower translational

diﬀusion process (model E in Fig. 3.23; after [97]). However, this result which

concerns the fast localized motions alone, is not unique, because there is a

second type of local diﬀusive motion (model B in Fig. 3.23 : two-site pro-

ton jumps in a non-linear H-bond [109]). It agrees equally well with the data.

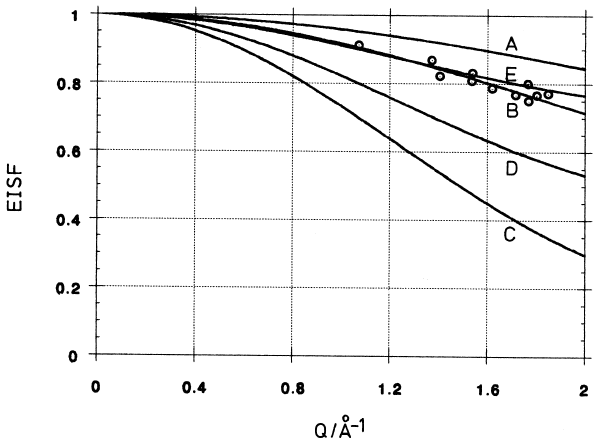
3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 135

Fig. 3.23. EISF data (circles) of CsOH · H

O, compared to ﬁve diﬀerent models

(Fig. 4 in [97] and Fig. 5 in [91]). A) two-site proton jumps in a linear H-bond;

B) two- site jumps in a non-linear H-bond; C) three-fold reorientation of OH

−

and H

O groups; D) three-fold reorientation of H

O molecules alone; E) three-fold

reorientation of OH

−

groups alone. An ambiguity remains: both models B and E

agree with the experimental results; compare Fig. 3.24.

Both types of local motion are apparently required as a combination to result

in translational proton diﬀusion through the crystal lattice. A Q-dependent

broadening, due to the latter motion, of the elastic spectral component was

observed at much higher resolution. The question, which one of the two local

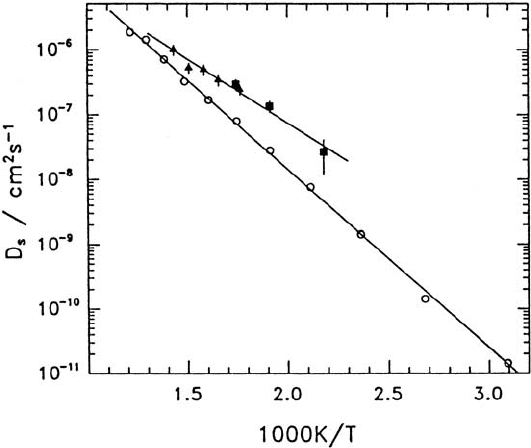
processes determines the rate of translational diﬀusion, was answered by the

study of this Q-dependent linewidth. Fig. 3.24 (following [91,97]) shows the

comparison of models B and E, mentioned above, to the measured line widths

(circles) which have been corrected for multiple scattering. Both models im-

ply Grotthuß mechanisms. In model B the intra-H-bond jumps are assumed

to have the higher rate; OH

−

−reorientations would consequently determine

the diﬀusion rate. In model E, the 120

◦

−

−reorientation (corresponding

to inter-H-bond jumps) is assumed to be the fast local motion, whereas the

proton transfer process within the H-bond represents the rate-determining

step of the diﬀusion mechanism. The ﬁgure shows clearly, that only model E

agrees with the data.

It should be emphasized, that the self-diﬀusion coeﬃcient D

from PFG-

NMR measurements was used to ﬁx the slope of the linewidth curve in the

low-Q limit (Fig. 3.24). This has been decisive for obtaining this unambiguous

136 Tasso Springer and Ruep E. Lechner

Fig. 3.24. TranslationalprotonjumpdiﬀusioninCsOH· H

O (Fig. 6 in [91];

after [97]): the measured quasielastic diﬀusion linewidths (squares) are compared

to the width functions Γ (Q) of models B and E. Only model E agrees with the

experimental results. The straight line corresponds to the low-Q limit Γ (Q)=D

of the width function, where D

is the proton self-diﬀusion coeﬃcient obtained from

PFG-NMR measurements [97]. The ambiguity mentioned in the legend of Fig. 3.23

has now been resolved.

result from the comparison of the theoretical curves to the measured neutron

data, and it is a demonstration of the usefulness of combining

H − NMR

techniques with QINS experiments on protonic conductors. The direct deter-

mination of D

by QINS, which requires low Q, is presently limited to the

regime D

≥ 10

−7

/s. Since at low Q, the linewidth is equal to D

,it

rapidly approaches the limit of timescale imposed by the best possible en-

ergy resolution. Therefore, when the QINS resolution becomes insuﬃcient,

it is recommended to resort to the NMR spin-echo technique employing a

steady-state or pulsed magnetic ﬁeld gradient (PFG) for the measurement

of the proton self-diﬀusion coeﬃcient D

(see Chap. 10). This allows one to

reach values down to about 10

−9

/s. They may be used as an input to

the analysis of large-Q QINS spectra, permitting to extract the unique geo-

metrical and dynamical information on the microscopic details of the proton

motion, contained in them. Note that at large Q the requirements of energy

resolution are much less stringent as long as the diﬀusion coeﬃcient is known.

Another important class of ion conducting substances are doped per-

ovskitesofthetypeA(BO

). For instance, Sr(CeO

) is ion conducting if

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 137

Fig. 3.25. Protonic self-diﬀusion coeﬃcient for the protonic conduction in a H

O-

vapour doped perovskite:

Ba[Ca

(1+x)/3

(2−x)/3

2−

(3−x)/2

; full squares, full triangles: D

from quasielastic

neutron scattering, Γ = Q

;opencircles:D

from electrical conductivity σ(T )

using the Nernst-Einstein equation [108], with H

set equal to 1.

afew(x)%oftheCe

ions are substituted by Yb

thus creating (x/2)

oxygen-site vacancies. This leads to oxygen conduction by the mobility of the

vacancies. If, in addition, the material is exposed to water vapour, the H

molecules disintegrate. All hydrogens are forming OH

−

ions and the hydro-

gen (proton) is highly mobile. Also in these materials, it is assumed that the

electrical conductivity of the substance is determined by proton transfer or

jumps between the oxygen atoms (OH–O→O–HO) combined with fast rota-

tions of the hydroxyl ions (Grotthuß process) [110]. Proton diﬀusion in a ce-

ramic strontium cerate was observed for the ﬁrst time by quasielastic neutron

scattering [111], with a value of D

roughly consistent with the experimental

conductivity σ. The hydrogen concentration was obtained by microgravime-

try. Similar experiments were carried out by Pionke et al. [108] for a mixed

niobate of the type Ba[Ca

(1+x)/3

(2−x)/3

(3−x/2)

, where the vacancies

are produced by the mixture of the 2- and 5- valent Ca and Nb ions. Fig. 3.25

compares the D

values resulting from QENS experiments extrapolated to

small Q, and the charge-diﬀusion coeﬃcient D

calculated by the Nernst-

Einstein equation from the electrical conductivities. The (unknown) Haven

ratio H

was set equal to 1. The approximate agreement suggests that the

conductivity is predominantly protonic, and not due to hole or electron con-

138 Tasso Springer and Ruep E. Lechner

duction. We emphasize that in impedance spectroscopy the bulk conductivity

is determined by an extrapolation procedure to eliminate the strong inﬂuence

of grain boundaries and electrode eﬀects on the electrical measurements. On

the other hand, the scattering experiments should not be inﬂuenced by grain

boundaries.

For large Q values, the quasielastic spectrum shows the superposition of

two Lorentzians in the µeV region. They were tentatively explained by two

groups of potential wells for the protons, namely shallow and deep ones de-

pending on the charge of the adjacent ions. Further experiments with low

resolution (∼ 0.1 meV) yield a very broad spectrum. It is interpreted by

rapid OH

−

rotations connected with the conduction process [108]. For a pro-

ton, rotating in the hydroxyl ion, and jumping from time to time between

neighboring O

−

ions, one expects an incoherent dynamic structure factor for

an isotropic powder sample.

inc

(Q, ω)=F (Q)e

−Q

u





/π

+ ω



+[1− F (Q)]e

−Q

u



/π

+ ω

(3.65)

This expression is again based on the approximation of dynamical indepen-

dence already described above. The ﬁrst term describes the translational

diﬀusion of the hydrogen atoms. The second term results from the OH

−

rotation, whereby the small additional broadening of this term due to trans-

lational diﬀusion has been neglected. F (Q) is the elastic incoherent structure

factor (EISF; see (3.18)) of the protonic motion on a spherical shell with a

radius ρ, namely (see [3])

F (Q)=



sin ρQ

ρQ



. (3.66)

The function exp(−Q

u

) is the Debye-Waller factor and u

 is the mean

square amplitude of the phonon vibrations. The width of the line Γ

is related

to the rotational diﬀusion coeﬃcient D

=1/τ

,whereτ

is the relaxation

time for the diﬀusion on the sphere. The rotational term holds approximately

for Qρ < 1. Otherwise, further terms have to be added with widths Γ

(1 + )D

( =1, 2,...). The experiments lead to a width Γ

=0.70 meV

at 670 K which does not depend on Q and yields 1/τ

=10

−1

.The

protonic transfer or jump rate is about 100 times smaller. The Q dependence

of the intensity for the (resolution broadened) central line corresponding to

the ﬁrst term is shown in Fig. 3.26. It yields F (Q), the EISF, and a value of

ρ =0.70

A. The value of ρ can be compared with the OH-distance in water

or ice which is about 1

A. These results are consistent with the Grotthuß

process introduced at the beginning of this section. They bear some striking

similarity to those observed in CsOH ·H

O by Lechner et al. [97] (see above).

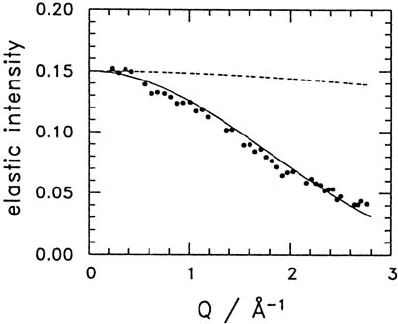
3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 139

Fig. 3.26. Intensity of the experimental narrow quasielastic line for the mixed

perovskite as in Fig. 3.25, vs. Q (black dots): The steep decrease vs. Q, corrected

for the Debye-Waller factor (dashed), yields the elastic incoherent structure factor

(EISF), calculated for OH

−

rotations with an average sphere radius of 0.7

A (solid

line) [108].

3.10 Proton Conduction: Diﬀusion Mechanism Based on

a Chemical Reaction Equilibrium

The Grotthuß type proton diﬀusion mechanism described in the previous

section, for instance in the case of CsOH · H

O, implies a simple chemical

reaction equilibrium between proton donor and acceptor molecules, which

reads: H

O+OH

−

⇐⇒ OH

−

O. An analogous reaction has been studied

in more detail in the solid-state protonic conductor Rb

H(SeO

)

[112,113].

The crystalline compounds with the general formula M

H(XO

)

, (M=K,

Rb, Cs; X=S, Se), where hydrogen bonding plays an important role, are

quasi two-dimensional solid-state protonic conductors (SSPC). They have

high-temperature phases with rhombohedral symmetry and extremely high

protonic conductivity. The crystallographic phases existing at lower tempera-

tures are monoclinic or triclinic and show lower but still appreciable protonic

conductivities in a fairly broad temperature range in the vicinity of the SSPC

phase transition [114, 115]. Information on the diﬀusive proton motion has

been obtained from a series of QINS studies on Rb

H(SeO

)

[112]. In the

following we will discuss results from a part of these experiments, where

medium-resolution QINS has been used. The time-averaged crystal structure

of Rb

H(SeO

)

[116–119] can be described as a sequence of Rb ···H[SeO

]

layers alternating with Rb-coordination polyhedra layers, both perpendicular

to the pseudo-hexagonal c-axis.TheatomsintheRb-layers,oftypeRb(2),

have 9-fold coordination by the oxygen atoms forming the bases (O(1), O(3)

and O(4)) of the selenate tetrahedra, which are parallel to the layers. The top

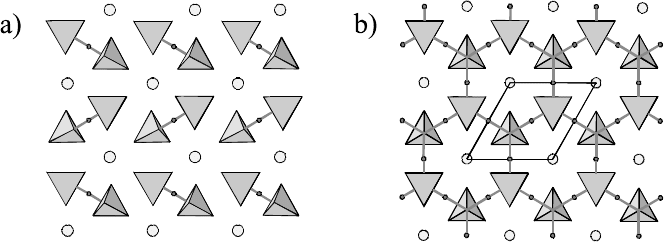
140 Tasso Springer and Ruep E. Lechner

Fig. 3.27. a) Monoclinic Rb

H(SeO

)

: “zero-dimensional” H-bond network as

seen in a projection along the c-axis. Small circles: protons; large circles: Rb

ions;

b) Trigonal Rb

H(SeO

)

: two-dimensional dynamically disordered H-bond network

in plane perpendicular to c-axis; after [113].

oxygen atoms (O(2)) of the selenate tetrahedra are inter-connected by hydro-

gen bonds, forming H[SeO

]

3−

dimers at low temperatures (see Fig. 3.27 a):

“zero-dimensional” H-bond network) and layers of two-dimensional dynami-

cally disordered H-bond networks in the proton conducting high-temperature

phase (T ≥ 449 K; Fig. 3.27 b)). The time averaged structure of the latter

is trigonal, space group (R

3m). The quasi-planar H-bond networks exhibit

a protonic conductivity exceeding, by an order of magnitude, that observed

along the c-axis which is perpendicular to these planes [114,115].

In the QINS measurements, translational proton diﬀusion occurring on

the 10

−8

s time scale was directly observed [120] as well as much faster local-

ized diﬀusive proton motions (time scales: 10

−9

sto10

−11

s [121]). Only the

latter will be discussed here.

An EISF study [112,122] suggests that the local proton-density distribu-

tion resulting from a limited time-average (from 10

−11

sto10

−10

s; ) already

has threefold symmetry. It comprises the regions of the three H-bonds con-

necting a given (selenate top) oxygen to its three neighbouring selenate top

oxygens in the same proton conducting plane (Fig. 3.28).

The “trigonal-asymmetric hydrogen bond” (TAHB) model [122] corre-

sponds to this picture: The local proton site arrangement comprises a central

site 1, with an average proton residence time τ

, connected by the jump

vectors R

, R

and R

to 3 external sites with identical residence times

. The 3 vectors (of equal lengths) point into the directions of the three

H-bonds (Fig. 3.29), with end points located fairly close to the bond centers.

The two jump rates, 1/τ

and 1/τ

, are allowed to be diﬀerent from each

other, implying an asymmetry of the potential in which the proton is moving

on the time-scale of this experiment.