Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 121

does not “see” this eﬀect since the distance between microcracks is much

larger than 1/Q.

3.6 Diﬀusion with Traps

In disordered alloys the potential for a diﬀusing atom ﬂuctuates randomly in

space, and the potential depth or binding energy changes from site to site,

as well as the barrier connecting adjacent sites. The calculation of the self-

correlation function G

(r, t) is possible by means of Monte Carlo methods and

only a simpliﬁed case can be treated analytically, namely by the so-called

two-state model [71]. We consider a regular lattice doped with impurities

at low concentration where the diﬀusing atom is temporarily bound by the

impurities. Under these circumstances, the problem is solved by treating the

diﬀusion as a random sequence of steps, namely an alternation between

– a free “state” where the atom diﬀuses in an undisturbed lattice, with a

self-diﬀusion coeﬃcient D

during an average time interval τ

and

– a trapped or immobile state during an average time τ

in the vicinity of

an impurity atom.

The self-correlation function is then obtained as a series expansion where each

term is a multiple convolution of the free and trapped-state self-correlation

functions. The “macroscopic” self-diﬀusion coeﬃcient D

is then related to

= D

+ τ

, (3.53)

and the free diﬀusion coeﬃcient is



6τ

. (3.54)

τ is the mean rest time on the undisturbed lattice sites and  is the corre-

sponding jump distance. The escape rate from the immobile trapped state

is 1/τ

; the rate of trapping can be calculated on the basis of a continuum

theory, namely

=4πR

eﬀ

(T )D

(T )c

. (3.55)

is the concentration of the impurities. R

eﬀ

is an eﬀective trapping ra-

dius. For an attractive potential caused by the impurity, R

eﬀ

decreases with

increasing temperature.

The results are schematically shown in Fig. 3.16. The width for an un-

doped crystal is presented by the dashed line following the basic Chudley-

Elliott result (3.30). For small Q there is only a single Lorentzian whose

width approaches Γ = Q

, related to the macroscopic diﬀusion coeﬃcient.

This is only obtained for suﬃciently small Q, namely such that the diﬀusive

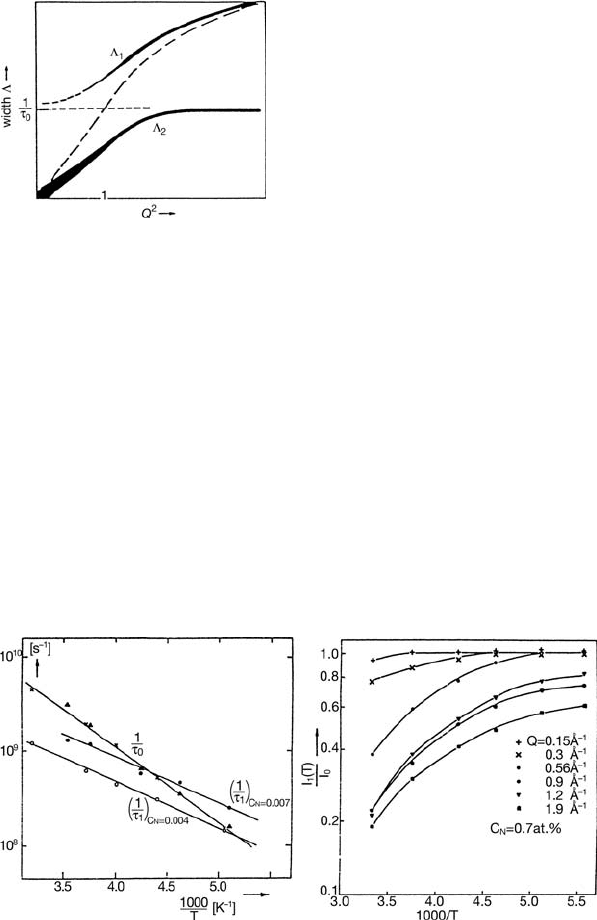
122 Tasso Springer and Ruep E. Lechner

Fig. 3.16. The two eigenvalues Λ

1,2

calculated for the two-state model correspond-

ing to the width of the quasielastic components Γ

1,2

vs. Q

. The line thickness

symbolizes the intensities of the two components. Dashed: Width for undisturbed

crystal. 1/τ

=escaperatefromtrap.ThemaximumvalueofΛ

is 1/τ

process is observed over a range larger than the average distance between the

impurities. At large Q,thetwo eigenvalues are visible in the spectrum. A

narrow quasielastic component appears whose width is related to the escape

rate of hydrogen from the trapping centres and whose intensity is propor-

tional to the fraction of atoms in the immobile state. In addition, there is a

broad component whose width approaches the jump rate in the undisturbed

lattice. Details of this model are found in [71] and in Chap. 18.

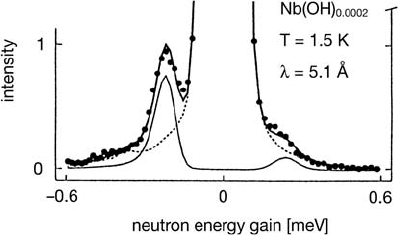
This behaviour has been observed and successfully interpreted for niobium

crystals, doped with 0.4 and 0.7 at % nitrogen and with 0.3 at % dissolved

hydrogen. Fig. 3.17 shows the intensity of the line related to the trapped

Fig. 3.17. Diﬀusion of H (0.3 mol %) in Nb doped with c

=0.4and0.7mol

% N atoms. Left side: τ

= average time of free diﬀusion, 1/τ

is proportional

to c

;1/τ

= escape rate, independent of c

. Right side: Intensity of the narrow

component in the quasielastic spectrum corresponding to eigenvalue Λ

. For small

Q: Single line with I

 1; for large Q: Intensity proportional to fraction of

trapped protons, increasing with decreasing temperature [71].

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 123

Fig. 3.18. Tunneling spectrum for Nb doped with 0.2 mol % H and 0.2 mol %

O. The hydrogen is trapped in a double potential well near the O impurity at

1.5 K. The asymmetry of the spectral doublet is due to the Boltzmann factor. The

intensity of the tunneling lines is only 1 % of the central elastic peak [73].

state. Expectedly for large Q the intensity of this narrow line (width  1/τ

)

decreases with increasing temperature because the H atoms spend a decreas-

ing fraction of their time near the N impurities. As seen from Fig. 3.17, the

trapping rate 1/τ

is proportional to the nitrogen concentration c

,whereas

1/τ

, the escape rate, is independent of c

. Both rates are thermally activated

with activation energies which, in a good approximation, can be understood

by elastic strain ﬁelds caused by the impurities. The model has also been

applied to a disordered alloy, namely Ti

1.2

1.8

where the free motion

cannot be clearly separated from the trapped state. Nevertheless, the evalu-

ation of the spectra yielded a consistent description of the spectra [68].

An interesting eﬀect is connected with hydrogen or deuterium dissolved

in niobium and trapped on impurities [72, 73]. It has been observed that

the speciﬁc heat for niobium doped with hydrogen or deuterium reveals an

anomaly at low temperatures with a strong isotope eﬀect if the sample was

loaded with a certain amount of oxygen or nitrogen. Investigations of neutron

spectra at low temperatures revealed two lines on the energy gain and loss

side. They correspond to transitions between stationary tunneling states of

the proton attached to the impurities, with energies of a few 0.1 meV. It

has been assumed that the N or O impurity occupies an octahedral site of

the bcc Nb lattice (see Fig. 3.11). This leads to two adjacent tetrahedral

sites separated by a low potential barrier where the proton wave function is

distributed over both sites. For a simple double-well model, with an exchange

integral J and an asymmetry  caused by the elastic distortions, one calculates

a tunneling splitting of

ω



+ 



1/2

. (3.56)

For hydrogen trapped on oxygen one gets J =0.22 meV,  =0.10 meV

depending on concentration, and for deuterium J =0.02 meV (Fig. 3.18).

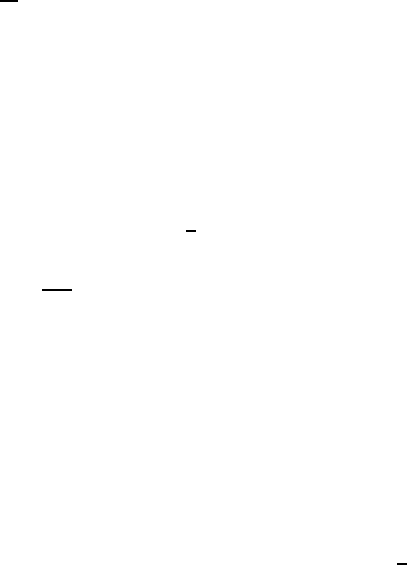
124 Tasso Springer and Ruep E. Lechner

3.7 Vacancy Induced Diﬀusion

In many metals the atoms diﬀuse in the presence of thermally induced va-

cancies. These vacancies themselves diﬀuse rapidly through the lattice, and

each jump of a vacancy is connected with a jump of a lattice atom. For dilute

vacancies, a selected atom undergoes a jump to a neighbouring site whenever

it has an “encounter” with a vacancy, where the time between jumps of the

vacancy τ

 10

−12

s is short compared to the time between two encounters

with diﬀerent vacancies, τ

 10

−9

. Normally, one and the same vacancy

leads to several correlated jumps of the same atom, such that one encounter

comprises a number of jumps where the sequences are still short compared

to τ

(see Chap. 1).

As a consequence, for incoherent scattering by the nuclei in the lattice,

the quasielastic spectrum can be calculated in the framework of the Chudley

Elliott equation (3.25) where the rapid jump sequence during the encounter

is treated as instantaneous. One obtains [74]

Γ =



1 −



all r

w(r

)cosQr



. (3.57)

w(r

) denotes the probability that, during the encounter, the atom was orig-

inally at r

= 0 and has reached the lattice site r

by one or several jumps.

The sum includes a term w(r

= 0) where several jumps of the sequence led

the atom back to its origin. The probabilities w can be calculated by computer

simulation [75]. Detailed theoretical investigations on the encounter model,

also including diﬀerent types of jumps, can be found in the literature [76]. If

the encounter consists only of a single jump, in a bcc metal it reaches only

the n = 8 nearest neighbours with r

≡ 

111; one has

Γ =

nτ



k=1

[1 − cos Q

] . (3.58)

It should be emphasized that the rapid jump sequence during the encounter

causes an additional quasielastic spectrum. However, the corresponding jump

rate 1/τ

 10

−1

is very large compared to 1/τ

 10

...10

−1

.Conse-

quently, the spectrum is 10

to 10

times broader than the spectrum related

to Γ (Q) in (3.57); in a high-resolution experiment designed for the study of

the encounter rate, 1/τ

, this is practically an unobservable background. In

a lattice with coherently scattering nuclei, in principle, one should observe

also vacancy diﬀusion itself, where the missing atoms have the cross-section

of the atoms. Quasielastic scattering concerning the diﬀusion in sodium sin-

gle crystals has been investigated and the diﬀusion is dominated by

[111]

jumps [74,77]. A detailed study has been carried out for the diﬀusion in bcc

titanium single crystals whose results are shown in Fig. 3.19 [78]. The depen-

dence of the quasielastic width in the µeV-region is consistent with jumps of

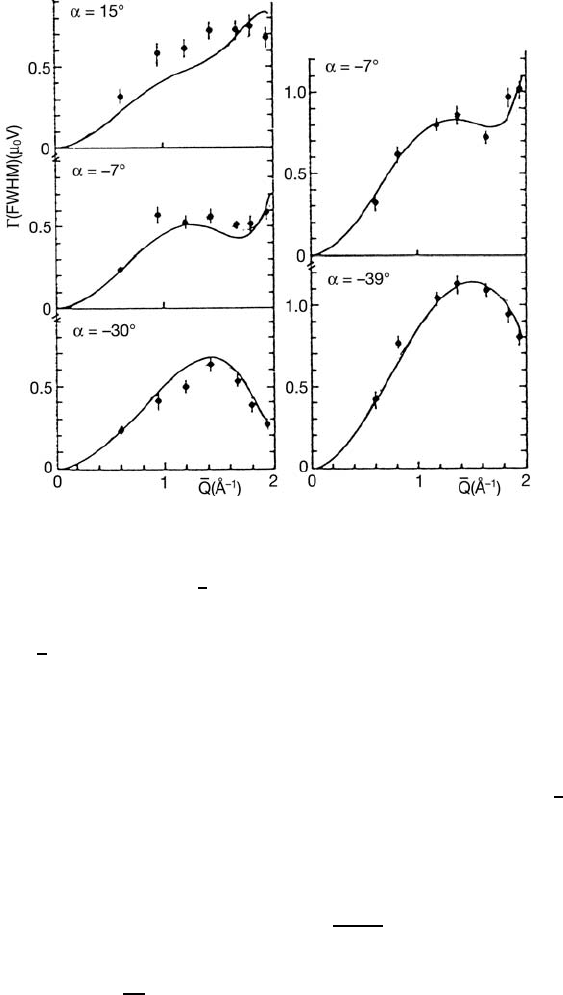
3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 125

Fig. 3.19. Quasielastic scattering width for vacancy induced diﬀusion of Ti in a bcc

single crystal. Γ (Q)isthefull width at half maximum. Diﬀerent orientations are

indicated (α = [110] ∧ k

). Left: 1460

◦

C, right: 1530

◦

C. Full circles: Experiment.

Solid line calculated for

[111] jumps with correlations during encounter [78].

the

[111] type including the contribution of next nearest neighbour a[100]

jumps. The high diﬀusion coeﬃcients of bcc alkali and group IV metals, with

relatively low activation energies has stimulated the investigation of phonon

dispersion curves of such substances, i.e. the relation between the propagation

vector q and the phonon frequency ω. Fig. 3.20 shows such results [79] for a

titanium single crystal. A rather low transverse acoustic mode can be recog-

nized, and, in particular, the collapse of a phonon branch near

[111] where

the phonon line degenerates and becomes a relaxation spectrum centered

at energy transfer ω = 0. It is possible to establish a systematic relation

between phonon frequencies ω

∗

and the activation energy E

∗

for diﬀusion,

namely

∗

∝

∗

, (3.59)

where T

is the melting temperature. This relation is plausible since for a co-

sine potential

∗

cos(πx/) the curvature is proportional to the activation en-

ergy E

∗

, and the squared frequency ω

∗

is proportional to the curvature [80].

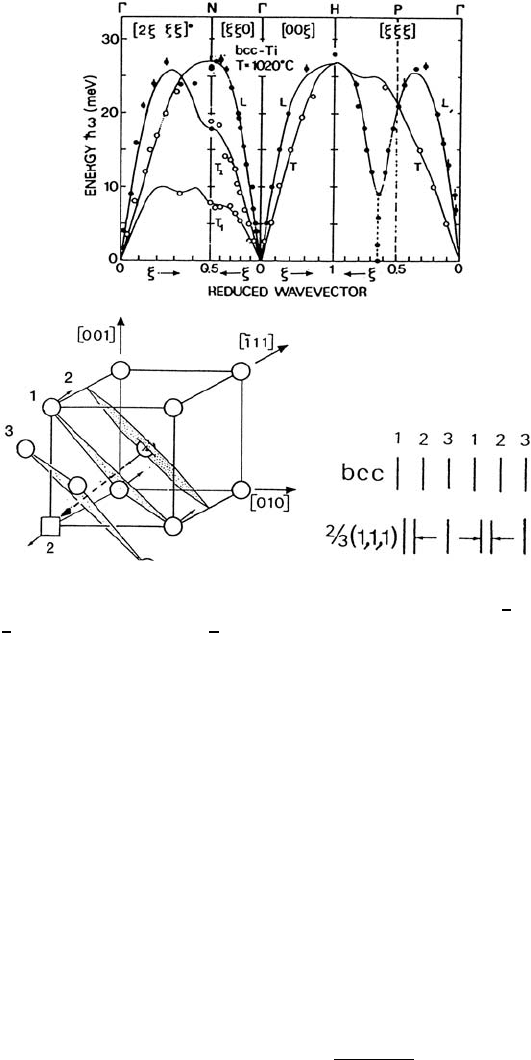
126 Tasso Springer and Ruep E. Lechner

Fig. 3.20. Top: Phonon dispersion curves ω(q)(ξ = q/q

max

) for a Ti single crystal.

Anomalies for the transverse acoustic [211] branch and for q =

[111]. Bottom: The

[111] phonon assists the

[111] jump into a vacancy at the cube corner, combined

with an opening of the transition through plane 1 by a [110] mode (from [79], see

also Sect. 2.3.1 in Chap. 2).

3.8 Ion Diﬀusion Related to Ionic Conduction

At elevated temperatures many materials, such as high-temperature solid

modiﬁcations of salts and their melts, certain solid metal hydroxide hydrates,

solid acidic salts and hydrates, and concentrated aqueous solutions of acids

are ionic conductors with electric conductivities σ of similar orders of magni-

tude in the solid and in the liquid state. Especially amenable to quasielastic

neutron scattering studies are those ionic conductors, where the charge car-

riers are negatively or positively charged hydrogen atoms (i. e. protons in the

latter case).

The connection between ionic diﬀusion and conductivity is given by the

Nernst-Einstein equation, which relates σ with the ionic charge diﬀusion co-

eﬃcient D

,namely

= σ(T )

(n · e)

. (3.60)

3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 127

Here N is the number density of the mobile ions, e the electron charge,

(n · e) the module of the charge of the mobile ions (n =1inthecaseof

hydrogen ions); k

is the Boltzmann constant, and T the temperature . The

relation between the atomic self-diﬀusion coeﬃcient, D

, obtained from neu-

tron scattering by the nuclei of the diﬀusing ions, and the charge diﬀusion

coeﬃcient, D

, determined by the measurement of the ionic conductivity,

is deﬁned by the Haven ratio, H

= D

. The latter quantity, a priori

unknown, takes into account correlation eﬀects occurring in ion diﬀusion,

such as deviations from directional and/or temporal randomness of consec-

utive ion jumps and, perhaps even more important, cooperative phenomena

involving the correlated diﬀusive motion of more than one charge carrier. Be-

cause of the Coulomb interaction between neighbouring ions, such eﬀects can

be particularly important in ionic conductors. Since correlation eﬀects are

practically always present, H

may have values between slightly smaller or

larger than 1, but may also be larger than 1 by an order of magnitude, as in

the case of cation diﬀusion in LiNaSO

[81], or even larger by several orders

of magnitude, as observed with the PFG-NMR technique (see Chap. 10) in

the cubic phase of very pure NaOH [82]. The latter observations have been

explained as the result of cooperative ring exchange mechanisms with no or

minor charge separation. A cation leaving its site induces correlated jumps of

neighbouring ions in the opposite direction. While the original cation jump

still contributes to self-diﬀusion, the backward-correlated jumps of neigh-

bouring ions strongly reduce the eﬃciency of charge transport. Beyond the

mere measurement of D

, and of microscopic quantities, such as residence

times and jump distances, QENS can give access to further information on

such correlation phenomena [83], as will be discussed below.

At higher temperatures, atomic or ionic jump rates in the crystal lattice

may become so large, that they are no longer well separated from the lower

part of the phonon frequencies. As a consequence, even at very low concen-

trations of the mobile particles (high concentration of empty sites) the simple

CE model breaks down, memory eﬀects appear, i.e. the diﬀusing atom “re-

members” part of its history, and therefore a step of the diﬀusional motion

will to some extent depend on the previous step(s). This eﬀect is mediated

by the lattice during the time of mechanical relaxation from the local dis-

tortion caused by the diﬀusing ion. Thus phonons may assist the diﬀusion

process (see Sect. 3.7) and for instance lead to more than one consecutive

nearest-neighbour jump at a time. An example for this case has already been

discussed in Sect. 3.5.

If, however, the concentration of diﬀusing species is high (low concentra-

tion of vacancies), it becomes necessary to take account of the correlations

between diﬀerent diﬀusing ions, because the probability of neighbouring sites

being blocked due to the presence of other mobile particles, is ﬁnite. Since

the theoretical treatment is very diﬃcult, Monte Carlo techniques have been

employed. At suﬃciently high ion concentration, the problem can be treated

128 Tasso Springer and Ruep E. Lechner

as a random walk of vacancies. One of the useful concepts for this case is the

encounter model already mentioned in Sect. 3.7, which has been developed

by Wolf [76]. An encounter is deﬁned as the ensemble of diﬀusional jumps

resulting from the interaction of a vacancy with a particular ion. At very low

vacancy concentration the duration of the encounter is short, as compared to

the average time interval τ

between two consecutive encounters of the same

ion with diﬀerent vacancies. Therefore, diﬀerent encounters are uncorrelated

and the ionic diﬀusion can be treated as a random series of discrete encoun-

ters. Spatial and temporal correlation eﬀects are caused by the fact, that the

ion performs, on the average, more than one single jump during an encounter

with a particular vacancy. The QENS function, derived in a way analogous

to the case of the simple CE model, is a Lorentzian, formally identical with

the expression on the right side of (3.31), where however the linewidth Γ is

now given by (3.57).

The encounter model has been applied to the “superionic” anion con-

ductor SrCl

and compared to various versions of the CE model by Dickens

et al. [84] and Schnabel et al. [85]. SrCl

has the ﬂuorite structure which

may be described as a simple cubic array of anions, with cations occupying

every other cube center. Because of the relatively large incoherent scatter-

ing cross-section of the chlorine nucleus, (5.5 barn), the QENS technique is

readily applied. In the region of the ‘diﬀuse’ transition around T

= 1000 K,

anionic conductivity and self-diﬀusion coeﬃcient rise rapidly up to values

approaching those of the molten salt. The quasielastic linewidths measured

at 1053 K in three diﬀerent crystallographic directions of a single crystal are

shown in Fig. 3.21 [84] as a function of the scattering vector Q, together

with theoretical width functions of three diﬀerent models. In particular, the

simple CE model (broken line) is compared with two models taking account

of correlation eﬀects, namely a CE model with nearest neighbour (nn) and

next nearest neighbour (nnn) jumps, i.e. forward correlated double jumps

(full line), and the encounter model (chain curve). The latter models are in

better agreement with the experimental data than the former. An important

result of this work is the proof, that the diﬀusion mechanism essentially in-

volves only the regular sites of the simple cubic (sc) anion lattice. This is

contrary to previous conjectures with respect to interstitial sites, but consis-

tent with the conclusions from tracer and ionic conductivity measurements,

at lower temperatures, by B´eni`ere et al. [86]. Another important result is the

conﬁrmation of the phenomenon of neutron diﬀraction by the single particle

probability density distribution (PDD) extending over a large region of the

lattice of diﬀusion sites at long times (see discussion in Sect. 3). The curves

in Fig. 3.21 clearly show a zero value of the QENS width function in the

[001] direction, where the location of the (002) reﬂection of the SrCl

ﬂuorite

lattice is indicated by an arrow. If the coherent (001) reﬂection (correspond-

ing to the pair correlation function) of the sc Cl

−

sublattice (with half the

lattice spacing) were observable, it would be located at the same place. This

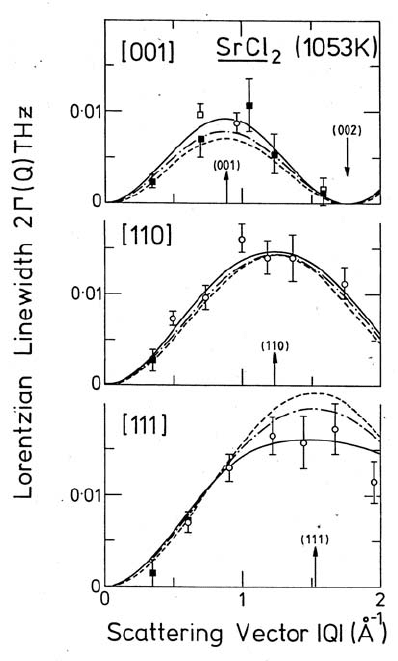
3 Diﬀusion Studies of Solids by Quasielastic Neutron Scattering 129

Fig. 3.21. Superionic anion conductor SrCl

: Quasielastic width functions mea-

sured at 1053 K (after Fig. 2 of [84]); dashed line: simple CE model with nn jumps

only; full line: CE model with nn and nnn jumps, i.e. with forward correlation;

chain curve: encounter model implying spatial and temporal correlation.

demonstrates, how incoherent neutron scattering can be employed as a means

for determining the structure of the lattice of diﬀusion sites in a crystal, pro-

vided the structure of the latter is known. Such structure determination is in

fact implicitly carried out, when lattice diﬀusion models are ﬁtted to QENS

spectra.

Another anion conductor, Ba

NH, is of special interest. The charge car-

rier is the H

−

ion, the ionic conductivity is extremely high (1 S cm

−1

near

700 K [87]), and it is essentially two-dimensional. This compound has a lay-

ered trigonal structure (space group (R

3m)), with separated H

−

and N

3−

ion layers, these ions being alternately located in the centers of distorted

Ba-octahedra. The analysis of quasielastic neutron scattering spectra, using

130 Tasso Springer and Ruep E. Lechner

a planar CE diﬀusion model, has shown that the H

−

diﬀusion process takes

place by uncorrelated jumps between regular hydrogen sites of the trigonal

lattice [88]. The scattering function of a two-dimensional diﬀusion process

has a singularity at zero energy transfer, and an analytical expression was

not available. Therefore a numerical method of calculating the distribution

of Lorentzian linewidths was used for comparison to the measured spectra.

According to crystallographic studies, about 15 % of the hydrogen ions are

on interstitial sites; therefore, a large amount of vacancies must exist on the

regular lattice of the basal plane. As a result, the self-diﬀusion coeﬃcient is

very high: D

=2.1·10

−5

/s at 823 K. The mean residence time of the H

−

ion in a regular lattice site was found to be 20 ps at this temperature. How-

ever, the authors do not mention the contribution of the 15 % of hydrogen

ions on interstitial sites, nor do they discuss their role in the diﬀusion mecha-

nism. In this example, the question of low-dimensionality has been implicitly

addressed by the numerical calculation of the linewidth distribution speciﬁc

for two dimensions. For further experimental results on low-dimensional dif-

fusion and a discussion of theoretical results concerning 2D-diﬀusion we refer

to Sects. 3.9 to 3.11.

Cationic conductors like AgI or RbAg

are another family of ionic crys-

tals with very high concentration of charge carriers, where all or most of the

mobile metal ions contribute to the electrical conductivity. Again a more so-

phisticated description is required to take into account ion-ion correlations.

For this situation Funke [89] has developed a concept to calculate S(Q, ω),

which has many features in common with the Debye-H¨uckel theory of ionic

liquids (see Chap. 21). We assume that an atomic jump occurs at the time

t = 0 from an equilibrium lattice site A to another site B. For small times t,

the site B is still unrelaxed and Coulomb repulsion has reduced the barrier for

a reverse jump, where the particle moves back to A over a barrier lower than

in the relaxed state. Now the particle has the choice, either to jump back,

or to stay on B, until the surrounding charges have relaxed such that a new

equilibrium situation has developed (this situation is similar to the one for the

strain ﬁeld shown in Fig. 3.14). We introduce a probability W (t) that a back

jump has not occurred until time t. This implies W (0) = 1 and W (t →∞)

approaches a ﬁnite value W

∞

such that the ionic self-diﬀusion coeﬃcient is

= W

∞



/6τ. Then the Chudley-Elliott equation can be rewritten, reduc-

ing the right side of (3.25) by a “success factor” W (t). Integration of this

equation then yields

,t)=δ(r



W (t−t



)



−



sτ



v=1

+ l



)





(3.61)

After Fourier transformation, W (t) can be related to the complex conductiv-

ity ˜σ(ω), and we introduce