Heard D.E. (editor) Analytical Techniques for Atmospheric Measurement
Подождите немного. Документ загружается.


112 Analytical Techniques for Atmospheric Measurement
noise considered here is the laser amplitude modulation (AM) noise that is within
the measurement bandwidth and centered on the measurement detection frequency.
This noise source is laser dependent, but is influenced by conditions of operation. For
example, laser-operating conditions where multiple lasing modes are simultaneously
present will experience intermode partitioning noise. This noise source, along with optical
feedback caused by scattering from various optical components, adds to the laser excess
noise. Solid-state lasers also exhibit frequency modulation (FM) noise, which, although
in many cases is quite small, causes amplitude noise vis-à-vis an absorption feature.
Residual amplitude modulation (RAM) is another potential noise source not considered
in Equation 2.25. This noise source, which depends on the particular laser and operating
conditions, results from the fact that the laser amplitude changes as the frequency is
scanned and/or modulated. It can also produce a large background signal, which can
totally mask absorption features of interest.
The AM noise from both the laser and detector fall off with a 1/f ‘pink noise’ frequency
dependence, which in the case of lead-salt diode lasers can plateau at frequencies as
high as 200 MHz (Werle et al. 1989) or at frequencies as low as 1 MHz (Carlisle et al.,
1989). Near-IR diode lasers also show this 1/f source dependence but roll off at different
frequencies (Hollberg et al., 1998). The shot noise, which originates from the discrete
nature of the generation of photoelectrons (Werle et al., 1989), is frequency independent
(White noise) but is proportional to the square root of the laser power incident on the
detector. The thermal noise, which arises from the Johnson noise of the detector and
preamplifier components and the inherent thermal noise of the detector, is independent
of both laser power and frequency. Hence, both the White-type shot noise and the
thermal noise are proportional to the square root of the detection bandwidth.
From the discussion above, one observes that at high enough frequencies the
spectrometer noise will no longer be dominated by the 1/f laser excess noise. In this
case, the frequency-independent thermal and shot noise contributions will determine the
SNR, and optimum quantum-limited performance is achieved whenever the shot noise is
equal to or greater than the thermal noise (Werle et al., 1989). Thus, in order to achieve
the highest measurement sensitivities with IR spectrometers employing solid-state laser
sources, the detection frequency should be as high as possible. However, additional noise
sources than those considered above typically dominate most IR spectrometers, and, as
we will see, the optimum detection frequency becomes a tradeoff between excess source
noise and the stability of the spectral background structure (Werle, 1995).
In all IR spectrometers, optical noise ultimately plays a dominant role in determining
the stability of this background structure. As in all lasers, the light from cw tunable solid-
state laser sources is highly temporally coherent, and, as a consequence, light scattering
from any optical element in the beam path may ultimately impinge on the detector along
with the primary beam. Since the detector output is responsive to all such beams, the
primary signal of interest can reside on top of an undulating background structure. In
many cases, this structure contains multiple frequencies, amplitudes, and time constants
from multiple scattering sources. In many cases, optical windows and beam splitters may
be the cause of such multiple beam paths. Every optical system contains at least one
window, and most likely several windows mounted on laser dewars, multipass absorption
cells, and detectors. Even in a perfect system with no scattering, small movements of any
optical element in the beam path will translate to small movements of the primary beam

Infrared Absorption Spectroscopy 113
on the detector, which can produce phase and amplitude noise fluctuations. Such optical
sources of noise are frequently referred to in the literature as ‘etalon’, ‘etalon fringe
noise’, or ‘optical interference fringe noise’, even though a classic fringe structure may not
be present. Throughout the rest of this chapter, we collectively designate all such noise
sources as ‘optical noise’. In some cases, variable background structure may be caused by
variable ambient absorption from molecules such as H
2
O-vapor in the open absorption
path external to the multipass cell. Here the pressure-broadened wings of H
2
O-vapor
could significantly change the background curvature for the analyte gas of interest, even
when the H
2
O absorption feature is 02cm
−1
away from the feature of interest (Fried
et al., 1998a). It is also entirely possible that unidentified, very weak absorption features
from other atmospheric molecules may play a role in changing the background structure.
Depending upon the experimental particulars, optical noise from the above sources yields,
with very few exceptions, equivalent A
min
values somewhere in the 10
−4
–10
−7
range. We
will now present the various measurement approaches employed in atmospheric studies,
which attempt to minimize these various noise sources.
2.5.1.3.2 DIRECT ABSORPTION
The first approach is based on direct absorption. In this method, the laser wavelength
(frequency in cm
−1
) is rapidly scanned over absorption features of the target molecule,
and mixing ratios are deduced from measurements of incident and transmitted inten-
sities, sample pressure and temperature, and pathlength, employing the Beer–Lambert
absorption relationship presented earlier. The scan is typically accomplished by scanning
the injection current to the laser source while holding the laser temperature fixed. Since
the current scan also affects the laser temperature, both tuning mechanisms become
important whenever the laser is slowly scanned, resulting in a changing laser current–
temperature relationship from scan to scan (Jennings, 1980). Jennings and subsequently
Fried et al. (1988) have shown that this effect can be eliminated by rapidly sweeping
the laser tuning current (at frequencies ≥∼20Hz) over the absorption feature in a time
that is fast compared to the thermal time constant of the laser crystal. This technique is
known as sweep integration.
Direct absorption spectra acquired using sweep integration are carried out by applying
a sweep ramp, usually a saw tooth ramp, to the laser injection current, and the detector
signal thus acquired is co-averaged in a computer or signal averager as the laser is
repetitively swept over the same absorption features. In some implementations of this
approach, a small fraction of the main IR beam is split off and sent through a reference
cell containing the target gas of interest. This reference channel is used to co-align spectral
absorption features before co-averaging so as to avoid smearing and degradation of the
resultant spectrum. Zahniser et al. (1995) have employed sweep integration with a lead-salt
diode laser using 100 discrete ramp steps at a 300 kHz rate, resulting in sweep frequencies
of 3 kHz. Nelson et al. (2002) from the same laboratory have extended this approach
to pulsed non-cryogenically cooled QC lasers for detection of NO. These researchers
employed a pulse rate of 1 MHz, which produced a 10 kHz sweep rate for a 100-point
spectrum. Richard et al. (2002) employed a 100 Hz sweep ramp to acquire absorption
features of CH
4
in the upper troposphere/lower stratosphere. In all the direct absorption
measurements just discussed, absorption features are fit to Voigt profiles using nonlinear
least-squares fitting routines together with the Beer–Lambert absorption expression.

114 Analytical Techniques for Atmospheric Measurement
The most popular routine for this purpose is the Levenberg–Marquardt nonlinear least-
squares algorithm published by Marquardt (1963). Since the direct absorption approach is
based upon fundamental principles, no calibration standards are required. This approach
can be further used to measure and/or verify the concentration of calibration standards
where such standards are employed. However, based upon our experience in the field, it is
highly desirable in all cases to periodically introduce calibration standards near the system
inlet entrance. This minimizes potential systematic errors from inlet/cell surface losses,
particularly on airborne platforms where one samples over a wide range of temperature,
pressure, and relative humidity conditions.
Employing direct absorption, Nelson et al. (2002), Hori et al. (1999), and Zahniser et al.
(1995) routinely achieve minimum detectable line centre absorbance values, A
min
, (at the
1 precision level) of 1–3×10
−5
using a 210 m pathlength for 1 second of averaging. This
corresponds to minimum detectable mixing ratios of 120 pptv Hz
−1/2
, 80 pptv Hz
−1/2
,
and 55 pptv Hz
−1/2
, for NO, NO
2
, and NH
3
, respectively. Using Equation 2.24, this
corresponds to pathlength-normalized absorbance values of 5 ×10
−10
cm
−1
Hz
−1/2
to
14 ×10
−10
cm
−1
Hz
−1/2
. It is important to emphasize that these performance estimates
represent the true instrument figure of merit, since they were obtained from the rms noise
of repetitive background measurements. As discussed by Tittel et al. (2003, and references
therein), the true figure of merit of a real world instrument is the ability to replicate the
same result when one samples a constant input concentration. This is in contrast to high
frequency baseline noise or measurement precision of a limited number of scans. Since
low frequency noise sources from a variety of causes may also be important, the ability to
replicate the same answer from many successive measurements can be far worse than the
inherent sensitivity of a single or small group of scans. The study by Fried et al. (1998a)
further illustrates this fact. Unfortunately, in many cases instrumental figures of merit
are too optimistic since they are not based upon such replicate measurements from a
time series, particularly under field conditions. This all too frequently obfuscates the true
comparison between techniques.
As with the examples above, it is essential when discussing instrument performance
to present the complete set of conditions under which such determinations are carried
out. An ideal comprehensive assessment should contain the following detailed infor-
mation: the sampling pathlength, the level of precision, the measurement time, the
measurement bandwidth, the minimum detectable mixing ratio, the corresponding line
centre absorbance, the measurement platform and sampling conditions, and finally an
assessment as to the performance reproducibility (i.e. a statement as to whether or not
such performance can be routinely obtained on a day-to-day basis or every once in
a while). A performance histogram is ideal for this purpose (see Figure 11 of Tittel
et al., 2003). Although the measurement time and measurement bandwidth are inter-
convertible, this conversion is complicated by the fact that different techniques employ
different frequency selective filters, different number of scans and fitting points. This
opens up the possibility that the inter-conversion may not be treated the same for each
study reported in the literature. For this reason it is highly desirable to report both
A
min
normalized to the bandwidth as well as A
min
for 1 second of averaging, which in
many cases are equivalent. It is also highly desirable in this regard to report the A
min
value for the optimum averaging time using an Allan Plot, and this will be presented in
Section 2.5.1.3.6. We will attempt to indicate such comprehensive assessments wherever
possible in the remainder of this chapter.

Infrared Absorption Spectroscopy 115
The balanced beam and balanced ratiometric detection (BRD) methods are two variants
of the direct absorption approach successfully employed by a number of researchers.
In these approaches, the laser beam is split into a signal beam and a reference beam,
and both are detected using similar IR detectors. The signal beam passes through the
multipass sampling cell while the reference beam does not. The common mode noise
residing on both beams from laser excess noise, optical noise up to the beam splitter, and
laser power supply noise cancel under the right circumstances when the detector outputs
are either subtracted or ratioed in the logarithmic domain. For complete common mode
noise cancellation, the reference beam must be accurately scaled so as to approximate
the sample beam over the full scan range at the time of measurement. Hobbs (1997)
developed an electronic feedback circuit based upon the d.c. detector levels to adjust
and maintain the detector scalings without the requirement for an exact balance between
the two arms. In this BRD approach the net output signal depends upon the ratio of
the signal to reference arm currents, which changes when the signal beam is partially
absorbed by the sample gas of interest. Allen et al. (1995) have demonstrated noise-
equivalent absorbances as low as 2 ×10
−7
Hz
−1/2
in the near-IR spectral region. This
is close to the shot noise limit of their study. Sonnenfroh et al. (2001) employed this
technique with a quasi-cw, room-temperature, QC laser emitting in the near-IR spectral
region. However, in this study the noise-equivalent absorbance 9 ×10
−4
was degraded
considerably from the near-IR value due to large detector background currents and low
average laser power. A similar approach has also been employed with second harmonic
detection (to be discussed) by Zhu and Cassidy (1995) using two different near-IR lasers
in the 13–14 m spectral region. Based upon the replicate precision over 10 seconds
of scans, these researchers achieved a 1 rms baseline precision of 14 ×10
−6
using an
equivalent noise bandwidth of 1.25 Hz. These measurements were carried out in the
laboratory employing a White cell with a 4 m pathlength and 2f detection at 10 kHz.
2.5.1.3.3 WAVELENGTH MODULATION TECHNIQUES
The second and third primary measurement techniques commonly employed with
solid-state laser sources are based upon the closely related techniques of wavelength
modulation spectroscopy (WMS) and frequency modulation spectroscopy (FMS). As we
have discussed, sweeping the laser injection current rapidly changes the laser output
frequency, and typical sweep frequencies in the 25–3000 Hz range have been employed
for this purpose. One can also apply much higher frequencies in the kHz to MHz regime
to modulate the laser injection current as the frequency is simultaneously swept across
the absorption line or locked to the line centre. As discussed previously, it is desirable to
employ high measurement detection frequencies to minimize laser source noise as well as
other 1/f noise sources, and the modulation process enables detection at such optimum
frequencies.
Most atmospheric studies at the time of writing employ modulation frequencies in the
kHz regime, typically between 1 and 100 kHz, and this technique is known as wavelength
modulation spectroscopy (WMS), derivative spectroscopy,orharmonic detection. In most
applications, one typically detects the modulated absorption at twice the modulation
frequency (‘second harmonic’ or ‘2f detection’) using a lock-in amplifier set to 2f .As
shown in Figure 2.15, which depicts the resulting second harmonic spectrum as well as the
first harmonic 1f and direct absorption spectra, the second harmonic signal exhibits a
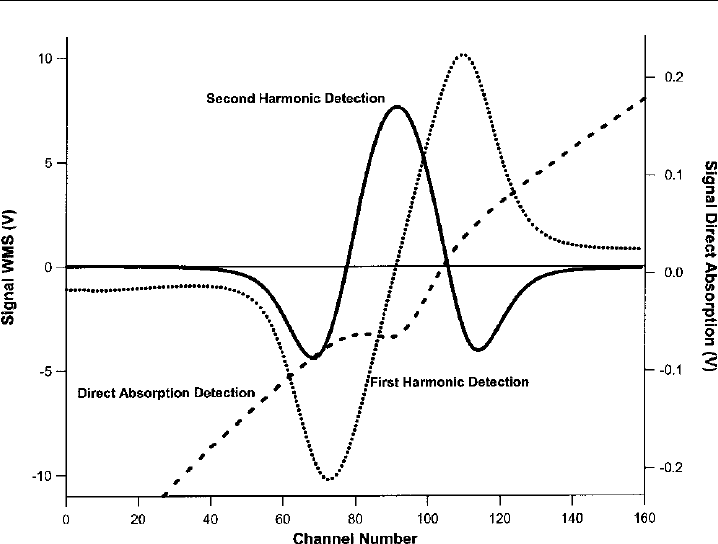
116 Analytical Techniques for Atmospheric Measurement
Figure 2.15 First and second harmonic wavelength modulation spectroscopy (WMS) signals in volts
(left-hand axis) along with direct absorption profile (right hand axis) for pure CO at 44.2 torr in a 16 cm
absorption cell (absorbance = 0018) using a the near-IR DFB laser at 1566 m. The harmonic and direct
absorption detection voltages have different gains (see text for an explanation of the different shapes).
(All spectra were acquired in our laboratory by Dr Petter Weibring.)
maximum at line centre and a baseline near 0 volts. The first harmonic signal, by contrast,
is zero at line centre, and the baseline, although flat, is nonzero. Higher harmonics may
also be used, but with each higher harmonic the signal is significantly decreased (compare
the 1f and 2f spectra of Figure 2.15). The 2f , as shown in Figure 2.15, reveals both
positive and negative lobes.
In addition to up-converting the detection frequency, both WMS and FMS techniques
produce a signal that is directly proportional to the mixing ratio of the target gas of
interest rather than a small change in a large signal, which is detected in direct absorption.
In both modulation cases, the background structure in theory is flat and at 0 d.c. Hence,
the amplification and digitization process, in the case of digital lock-in amplifiers, is
effectively centered around the absorption signal of interest rather than the large laser
intensity with its highly sloping background structure prevalent in direct absorption
measurements (see Figure 2.15). Furthermore, using modulation techniques, one can
choose the modulation frequency and/or amplitude to minimize optical noise structure
that may be present in direct absorption (Reid et al., 1980).
Finally, since modulation spectroscopy relies on a large change in the absorption
coefficient with wavelength (i.e. derivative-type response), modulation approaches can
help to discriminate against broad featureless absorptions, such as those from the wings

Infrared Absorption Spectroscopy 117
of atmospheric pressure-broadened water lines and those from big unresolved organic
molecules. As discussed in an earlier section, the larger the molecule the closer the
vibrational-rotational line spacings. Molecules, such as large organic gases, typically
containing five or more atoms will in most cases exhibit unresolved absorption features.
Although such features can change the modulated signal background structure and
curvature, they will generally not produce a modulated signal per se, even when spectrally
overlapped with the target molecule of interest. This aspect, which is in contrast to direct
absorption, becomes more important as an added degree of selectivity when measuring
trace gases in the atmosphere at levels below 100 pptv. However, this same aspect also
limits modulation spectroscopy to small molecules generally containing up to five atoms
and/or very narrow Q-branch transitions.
There have been many reviews of second harmonic detection, and three excellent
sources can be found in the book chapter by Brassington (1995), the detailed discussion
of the theory by Reid and Labrie (1981) and the application for the detection of HCl
by Fried et al. (1984). We only summarize the results here. For a sinusoidal modulation
at angular frequency and amplitude a (half modulation amplitude in cm
−1
), one can
write the time variation of the laser frequency (wavelength) about a mean value of as:
t = +m
v
cos (2.26)
One should not confuse the laser frequency in cm
−1
with the modulation frequency.
In Equation 2.26 the modulation phase angle t is replaced by and the modulation
amplitude a is normalized by the Voigt halfwidth at half maximum
v
to yield the
dimensionless modulation parameter m via:
m = a/
v
(2.27)
Incorporating the laser time dependence in Equation 2.26 in a cosine Fourier series, one
can write the second harmonic Voigt absorption coefficient, H
2
m, as:
H
2
m =
2
S
0
v
0
S
v
+m
V
cos y cos 2 d (2.28)
Here S
v
and S
0
are the Voigt absorption coefficients at the frequency determined
by the modulation and at line centre, respectively, and the term y has been defined
in Equation 2.19b. Equation 2.28, which is used to calculate the modulated absorption
coefficient centered around a specific frequency , reveals that a large number of
frequencies actually contribute to each value of the modulated absorption coefficient. At
line centre for example, the modulated absorption coefficient has contributions extending
from both wings of the absorption line, and as a consequence the maximum positive
second harmonic absorbance, which occurs at m = 22 (See Reid & Labrie, 1981),
is lower than the direct absorbance. The exact ratio depends upon the modulation
waveform applied (Iguchi, 1986). For the Voigt lineshape of Examples 1 and 2, the
positive lobe of the modulated absorbance at line centre, when normalized to that from
direct absorption, yields values of 0.36, 0.40, and 0.53, for sinusoidal, triangle, and
quasi-square modulation waveforms, respectively. The corresponding normalized peak-
to-peak second harmonic absorbance (sum of positive and negative lobes) yields values of

118 Analytical Techniques for Atmospheric Measurement
0.57, 0.62, and 0.86, respectively, for the three waveforms mentioned above. One obtains
slightly different ratios for Gaussian and Lorentzian lineshapes. However, in all cases,
the reduced modulated line centre absorbance relative to direct absorption is one of the
slight disadvantages of modulation spectroscopy.
Under optical thin conditions and a Voigt lineshape, Fried et al. (1984) and Reid
and Labrie (1981) have shown that the processed second harmonic signal S
2f
can be
expressed by the following expression:
S
2f
= CI
0
H
2v
mPNl (2.29)
In this expression C is a dimensionless proportionality constant, which represents the
second harmonic transfer function of the detector/preamplifier, lock-in amplifier, and
associated cabling. The a.c. gain is included in this term. As before, the term I
0
is the
incident laser intensity, which we assume in this expression does not change as we
modulate over the absorption line. This assumption is a good approximation when small
to moderate modulation amplitudes are employed (Reid and Labrie, 1981). The other
terms have been defined in Equation 2.23. Since the modulated absorption coefficient
at a particular wavelength has the same units cm
2
molecule
−1
as the direct absorption
coefficient, the second harmonic signal has the same units as I
0
(usually volts).
The proportionality term C and the dependence of the modulated absorption coefficient
on both the particular modulation waveform and modulation amplitude in Equation 2.29
indicate that the second harmonic signal is not a simple function of the absorber mixing
ratio. In contrast to direct absorption, where the absorber-mixing ratio is related to
fundamental instrument-independent quantities, second harmonic measurements contain
instrument-dependent factors. However, one can relate the absorber-mixing ratio to
fundamental quantities via indirect means for a fixed instrumental setup. May and
Webster (1993) described one procedure to determine the above proportionality constant
for a fixed modulation amplitude and waveform, which they designate as the ‘response
number’. In this analysis, the proportionality constant is determined from the ratio
of the observed to calculated peak-to-peak second harmonic signal normalized by the
absorbance. The d.c. and a.c. gains are included in this determination. An alternative
approach successfully employed by Fried et al. (1984, 1998b) uses a calibration standard
for another gas (reference gas, r) that absorbs in the same spectral region as the sample
gas s of interest. In this approach, using the same sampling pressure and pathlength,
one can express the ratio of the peak-to-peak second harmonic signals at line centre as:
S
2f
0
s
S
2f
0
r
=
I
0
s
I
0
r
H
2v
s
H
2v
r
s
r
(2.30)
Here the terms P l N and C in Equation 2.29 all cancel out, and one can solve for the
sample mixing ratio
s
from the ratio of second harmonic signals, laser powers, and
calculated second harmonic absorption coefficients. A third approach, which is employed
in most field studies, compares the sample second harmonic signal to that from a known
calibration standard (cal) for the same gas, in accordance with:
s
=
S
2f
0
s
S
2f
0
cal
cal
(2.31)

Infrared Absorption Spectroscopy 119
This approach assumes identical sampling conditions of laser power, sample pressure and
temperature, and pathlength, for both sampling modes. This approach has the advantage
in that it corrects to first order for any sample losses in the inlet line and sampling cell
during field operation. This approach, however, requires an accurate knowledge of the
calibration-mixing ratio, which can be obtained using direct absorption in the laboratory.
Our airborne measurements of CH
2
O, for example, employ both direct absorption and
the second harmonic ratioing approach given by Equation 2.30 (using methane standards
as the reference gas) in the laboratory before and after field studies. In this manner, we
realize the advantages of both an absolute calibration and a field calibration under a
variety of sampling temperatures, pressures, and relative humidities.
A range of A
min
values have been reported in the literature for 2f WMS detection
employing sweep integration. This range reflects many particulars of the studies, including
such factors as the pathlength employed, the specific type of laser used, and whether or
not the performance estimate is based upon laboratory or actual field measurements.
Since it is impossible to cite each and every reference, we only cite a few representative
examples. As discussed previously, Zhu and Cassidy (1995) report A
min
1 values of
14 ×10
−6
for laboratory studies using near-IR diode lasers, an equivalent bandwidth of
1.25 Hz, 2f detection at 10 kHz, and an electronic noise subtracting circuit. Bomse et al.
(1992) carried out very extensive laboratory studies comparing various measurement
approaches employing a single pass absorption cell. They report A
min
values of ∼8×10
−7
using WMS at frequencies of 100 kHz for 1 Hz equivalent detection bandwidths.
Our group has carried out extensive airborne measurements of CH
2
O employing 2f
WMS detection using a 100 m multipass absorption cell and a 35 m lead-salt diode
laser (Fried et al., 1998a, 1999a, 2003a,b; Wert et al., 2003a,b). These measurements thus
provide a rather extensive database on instrument performance during actual airborne
measurements. Over three different airborne campaigns (TOPSE 2000, TexAQS 2000,
and TRACE-P), Wert et al. (2003a) using various approaches report CH
2
O1A
min
values based on replicate measurements that fall within the range between 4 ×10
−6
and
13×10
−6
when extrapolated to 1-second averaging times. The lower limit is a factor of 2.5
improvement relative to the direct absorption values presented earlier. When integrated
over 1 minute, our results yielded A
min
values of 5 ×10
−7
to 18 ×10
−6
and minimum
detectable CH
2
O mixing ratios 1 of 15–55 pptv, with most values falling within the
range of 20–40 pptv. Normalizing to pathlength, these 60-second averages correspond
to 5 ×10
−11
cm
−1
to 2 ×10
−10
cm
−1
. A histogram for the entire spread of our airborne
CH
2
O performance during the TOPSE 2000 campaign can be found in Figure 11 of Tittel
et al. (2003).
In a variant of the 2f WMS approach just discussed, the laser is ‘line-locked’ to the
centre of the absorption feature rather than swept across the feature. As discussed by
Loewenstein (1988), this approach is advantageous for applications where rapid time
response is required and/or transient species are being observed in laboratory kinetic
studies. For this purpose, the zero-crossing signal of either the first or third harmonic at
line centre (see Figure 2.15) is used in a feedback loop to keep the laser locked to line
centre. Sachse et al. (1987) have successfully employed this approach on their DACOM
(Differential Absorption of CO Measurement) instrument to carry out fast airborne
measurements of CO, N
2
O, and CH
4
on time periods of ∼1 second. Typical airborne
line centre absorbance precisions were ∼2 ×10
−5
for a 0.03 Hz electronics bandwidth.

120 Analytical Techniques for Atmospheric Measurement
Loewenstein (1988) and Loewenstein et al. (1989) employed this same technique with
their ATLAS (Airborne Tunable Diode Laser Absorption Spectrometer) system to carry
out fast measurements of CO and N
2
O on NASA’s ER-2 high altitude research aircraft.
Optical noise represents the main performance limitation with this approach. However,
in contrast to sweeping over the absorption line, line-fitting analysis has not been utilized,
at least in past studies, to identify and minimize the effects of optical noise. Rapid
background subtraction (to be discussed), which can effectively capture and minimize
such noise sources, would certainly improve the measurement performance of line-
locking techniques further. However, at the time of writing, this approach has not been
typically employed with line-locking methods.
2.5.1.3.4 FREQUENCY MODULATION TECHNIQUES
In frequency modulation spectroscopy (FMS), one employs modulation frequencies that
are equal to or greater than both the laser and absorption linewidths. Typical frequencies
in this case fall within the range of several MHz to several GHz. As a result, one
can employ significantly higher modulation and sweep frequencies than WMS, and as
discussed previously, one can in principle achieve quantum-limited performance where
excess laser noise no longer dominates. The high frequency modulation
m
produces
multiple sidebands about the laser centre frequency
c
±n
m
, and the absorption line
of interest is probed by only one or two of these sidebands. In WMS by contrast, where
the modulation frequency is much less than the laser and absorption linewidths, one
can consider the absorption feature as being probed by a very large number of closely
spaced sidebands. The two main sidebands in FMS are equal in intensity and 180
out
of phase with one another, and as a result the signal at
m
is 0. The presence of an
absorber in the sample cell will negate this cancellation, producing a signal at
m
.As
discussed in the review by Brassington (1995), one obtains a positive absorption signal
as the first sideband passes through the absorption feature as the laser centre frequency
is swept. This is followed by a negative signal as the second sideband passes through the
absorption feature. This technique is called single tone FMS, or STFMS, and the detected
signal is processed by a double balanced mixer. This approach requires detectors with
bandwidths as high as several hundred MHz. Because such detectors in the mid-IR are
expensive, the technique of two tone FMS, or TTFMS, has been developed. In this case,
two closely spaced high frequency modulations, separated by ∼1–10 MHz, are applied
to the laser, and the detection is carried out at the 1–10 MHz beat frequency. Although
the laser excess noise is not completely eliminated, TTFMS significantly reduces detector
costs. Comprehensive theoretical discussions of FMS and comparisons with WMS can be
found in Silver (1992) and Bomse et al. (1992), and the reviews by Brassington (1995)
and Werle (2004), as well as the publications by Werle et al. (1989), Werle and Slemr
(1991), Werle (1995) and Werle and Jänker (1996), provide excellent background on
FMS techniques and their limitations.
Since FMS employs high frequency RF modulation, the experimental setup is more
complicated than that for WMS. The ultimate detection sensitivity of FMS spectrometers
is particularly dependent upon various laser parameters such as the laser power, noise
spectrum, and amplitude modulation index as well as the laser beam quality. The latter is
important since the optical radiation must ultimately be focused onto small area detectors
in order to achieve such high detection bandwidths in the case of STFMS. In addition, RF

Infrared Absorption Spectroscopy 121
pickup in the signal processing chain can also limit performance, and this further requires
careful shielding and impedance matching of the RF modulation frequency imposed on
the laser d.c. injection current. As discussed by Silver (1992), such impedance matching
is especially difficult to achieve with mid-IR lead-salt diode lasers in cryogenic housings.
The FMS techniques also exhibit additional practical difficulties. As discussed in the
above references by Werle and colleagues, optimum FMS signals are typically achieved at
much lower pathlengths than WMS (Werle and Slemr, 1991), thus placing restrictions on
minimal detectable mixing ratios that can be achieved. If both techniques are operated
with their optimal number of passes through their respective multipass cells, FMS can
improve the sensitivity only by approximately one order of magnitude relative to WMS
instead of two or more orders of magnitude anticipated in early studies (Werle and
Slemr, 1991).
There are additional drawbacks using FMS, which further minimize the performance
disparity with WMS in realistic field systems. High frequency modulation is more suscep-
tible to alignment instabilities (Werle, 1995) than lower frequency WMS techniques. At
modulation frequencies of 100–200 MHz employing STFMS, for example, Werle (1995)
calculates that short-term optical alignment stability must be less than 10 m to achieve
minimum detectable absorbances less than 10
−6
on a consistent basis. This compares to
optical stabilities in the mm range for WMS techniques. Werle and Jänker (1996) also
uncovered another drawback using FMS. Employing modulation frequencies of 100 MHz,
these researchers found that refractive index fluctuations generated by turbulent gas flow
through a multipass absorption cell produce phase and optical pathlength fluctuations
that limit performance. At flow rates of 10 liters min
−1
, such phase fluctuations limited
their A
min
to values in the range between 5 ×10
−7
and 7 ×10
−7
using integration times
of up to 10-seconds (Werle and Jänker 1996).
Bomse et al. (1992) describe a variant of the STFMS technique, which they term high
frequency WMS, to circumvent the drawbacks just discussed. In this case, the laser is
modulated at frequencies in the 1–20 MHz range and 2f detection is achieved using RF
mixers instead of lock-in amplifiers. Aside from this difference and the further reduction
in laser excess noise, high frequency WMS is identical to 2f WMS discussed earlier.
Bomse et al. (1992) report A
min
values in the low- to mid-10
−7
range for 1 Hz detection
bandwidths. Although this is a slight improvement over the WMS results presented earlier,
the laser can be swept over the absorption lines of interest at much higher rates than
with WMS. Typical WMS rates are 50–100 Hz, while rates for high frequency WMS are
≥500 Hz. This has two advantages: the measurement time is significantly decreased, an
important attribute for flux studies; and secondly, low frequency perturbations during the
laser sweep are minimized. Such perturbations can arise from such sources as mechanical
vibrations during aircraft operation and/or electrical perturbations on the laser sweep
ramp. However, the ultimate performance of WMS and FMS techniques are in most
instances dominated by optical noise. As a consequence, early optimism of exceedingly
low minimum detectable absorbances in the 10
−7
–10
−8
range for 1 Hz bandwidths in
select laboratory setups using single pass absorption cells (Carlisle and Cooper, 1989;
Carlisle et al., 1989; Werle et al., 1989) employing FMS has not been realized in realistic
field systems employing multipass absorption cells.
At the time of writing, the number of field studies employing FMS techniques
has been somewhat limited, with most of these studies using near-IR laser sources.
