Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


stationary
and
static
spacetimes;
time
translation
isometries
Kiliing
parameter
28.6
GENERAL
THEORY
OF
RELATIVITY
923
of which one camassign a three-dimensional space corresponding to the "spatial
universe" at that moment.
In the general theory
of
retativity, space
amd
time cam
be mixed, but the character of time as a parameter remains unaltered. Therefore,
instead
of
am
axis-s-a straight
line-we
pick a curve, a parametric map from the
real tine to the mamifoldof space-time. This curve mustbe
timelike, so that locally,
when curvature is ignored amdspecial relativity becomes a good approximation,
we do not violate causality. The curvemustalso have the property that at each point
of it, the space-time manifold has the same metric. Moreover, we need to demamd
that at each point of this curve, the spatial part of the space-time is orthogonal to
the
curve.
28.6.1. Definition. A spacetime is stationaryifthere exists a one-parametergroup
ofisometries F" called time translation isometries, whose Killing vectorfields
e
are timelikefor all t: g(e,
e)
>
O.
[fin
addition, there exists a spacelike hyper-
surface
E that is orthogonal to orbits (curves)
of
the isometries, we say that the
spacetime
is static. .
We camsimplify the solution to Einstein's equation by invoking the syunnetry
of spacetime discussed above
in our choice
of
coordinates. Let P be a pointof the
spacetimemanifoldlocatedin aneighborhoodof some spacelikehypersurface E as
shown in Figure28.2. Through P passes a singleorbitof the isometry, which starts
at a point
Q
of
E.
Let t, the so-called Killing parameter, stamdfor the parameter
correspondingto the point
P with t = 0 being the parameterof Q.On the spacelike
hypersurface
E,
choose arbitrary coordinates
{xi}
for Q. Assign the coordinates
(t
==
xO,
xl,
x
2
,
x
3
)
to P. Since F, does not chamgethe metric, E,
==
F,E,
the
tramslation of E by
F"
is also orthogonal to the orbit of the isometry. Moreover,
the components
of
the metric in this coordinate systemcannotbe dependent on the
Killing parameter t. Thus, in this coordinate system, the spacetime metric takes
the forru
3
9 = goodt ®
dt
- L
g'jdx
i
®
dx
j
.
i,j=l
(28.93)
spherically
symmetric
spacetimes
28.6.2. Definition. A spacetime is spherically symmetric if its isometry group
contains a subgroup isomorphic to
80(3)
and
the orbits
of
this group are two-
dimensional spheres.
In
other words, if we think of isometries as the action
of
some abstract group,
then this group mustcontain
80(3)
as a subgroup. Since
80(3)
is isomorphic to
the group of rotations, we concludethat the metric should be rotationally invariamt.
The time-tramslation Killing vector field
emust be orthogonal to the orbits
of
80(3),
because otherwise the generators
of
80(3)
camchamgethe projection of e
on the spheres
amd
destroy the rotational invariamce.Therefore, the 2-dimensional
spheres must lie entirely in the hypersurfaces
E,.
Now, we cam write down a
924 28.
DIFFERENTIAL
GEOMETRY
s
u
t
(28.95)
Schwarzschild
solution
of
Einstein's
equation
Figure28.2 The
coordinates
appropriate
fora
stationary
spacetime.
static spherically symmetric metric in terms of appropriate coordinates as follows.
Choose the sphetical coordinates
(0,
rp)
for the 2-spheres, aod write the metric
of
this sphere as
92 = r
2dO
I8i
so
+r
2
sin
2
Odrp
I8i
dtp,
where r is the ''radius''
of
the 2-sphere. Choose the third spatial coordinate to
be orthogonal to this sphere, i.e., r, Rotational symmetry now implies that the
components
of
the metric must be independent
of
0 aod
rp.
The final form of the
metric based entirely on the assumed symmetries is
9 =
f(r)dt
I8i
dt -
h(r)dr
I8i
dr
- r
2(dO
I8i
dO+sin
2
Odrp
I8i
dip).
(28.94)
Wehave reducedthe problem of finding ten unknownfunctions
{g
/LV
}~,
v=o
of
four
variables
{x/L
}~~o
to that of two functions f aod h of one variable. The remainiog
task is to calculate the Ricci tensor corresponding to Equation (28.94), substitute
it in Einstein's equation (with the RHS equal
to zero), and solve the resulting
differential equation for f aod h. We shall not pursue this further here, aod we
refer the reader to textbooks on general relativity (see, for example, [Wald 84,
pp. 121-124]). The final result is the so-called Schwarzschild solution, which is
(
2M)
(2M)-1
9 = 1 - --;:- dt
I8i
dt
- 1 - --;:- dr
I8i
dr
- r
2(dO
I8i
dO+sin
2
Odrp
I8i
drp),
where M is the total mass of the gravitating body, aod the natural units of GTR,
in which G = 1 =c, have been used.

28.6
GENERAL
THEORY
OF
RELATIVITY
925
A remarkable feature of the Schwarzschild solution is that the metric compo-
nents have singularities at
r =
2M
and at r =
O.
It
turns out that the first singularity
is due to the choice of coordinates (analogous to the singularity at
r = 0, e=0, n ,
and
rp
= 0 in spherical coordinates of
JR3),
while the second is a true singularity
of spacetime. The first singularity occurs at the so-called
Schwarzschild
radius
Schwarzschild
radius
whose numerical value is given by
2GM
M
rs =
--2-
""
3-
km,
c
M0
where M
0
= 2 x 10
30
kg is the mass of the Sun. Therefore, for an ordinary body
such as the Earth, planets, and a typical star, the Schwarzschildradius is well inside
the body where the Schwarzschild solution is
not
applicable.
If
we relax the assumption
of
staticity, we get the following theorem (for a
proof, see [Misn 73, p. 843]):
28.6.3.
Theorem.
(Birkhoff's theorem) The Schwarzschild solution is the only
sphericallysymmetricsolutionofEinstein'sequationin
vacuum.
A corollary to this theorem is that
28,6.4.Box. All spherically symmetric solutions
of
Einstein's equation in
vacuum are static.
This is analogous to the fact that the Coulomb solution is the ouly spherically
syurmetric solutionto Maxwell's equations in vacuum.
It
can be interpreted as the
statementthat in gravity, as in electromagnetism, thereis no monopole "radiation."
28.6.3 Schwarzschild Geodesics
With the metric availableto us, we can, in principle, solve the geodesic equations
[Equation (28.65)] and obtain the trajectories
of
freely falling particles. However,
amore elegantway is to make furtheruse
of
the syurmetries to eliminatevariables.
In
particular, Proposition28.4.4is extremelyusefulin this endeavor. Considerfirst
9(80, u) where u is the 4-velocity (tangent to the geodesic).
In
the coordinates we
are using, this yields
9(80,
u)
= 9(80, x
1L
8
1L
) = x
lL
9(80, 8
1L),
= r
2
0.
r280IJ-
This quantity (because
of
Proposition 28.4.4and the fact that
80
is a Killing vector
field) is a constant of the motion, and its initial value will be an attribute of the
particle
during
its
entire
motion.
Weassignzerotothis
constant,
i.e.,we
assume
that
initially 0 =
O.
This is possible, because by rotating our
spacetime-an
allowed

926 28. DIFFERENTIAL
GEOMETRY
operation due to rotational
symmetry-we
take the equatorial plane e= IT
/2
to
be the initial plane
of
the motion. Then the motion will be confined to this plane,
because (j = 0 for all time.
For theparameterof the geodesicequation, choosepropertime r if the geodesic
is timelike (massive particles), and any (affine) parameter
if
the geodesic is null
(massless particles such as photons). Then
gl'vil'iV
=
K,
where
K =
{I
for timelike geodesics,
o for null geodesics.
In terms of our chosen coordinates (with e= IT
/2),
we have
(28.96)
(28.97)
Next, we apply Proposition 28.4.4 to the time translation Killing vector and
write
(28.98)
where E is a constant
of
the motion and e=
at.
In
the case of massive particles,
as r
-+
00,
i.e., as we
approach
specialrelativity, E becomes i, whichis therest
energy
of
a particle
of
unit mass.l'' Therefore, it is natural to interpret E for finite
r as the total energy (including gravitational potential energy)
per
unit mass of a
particle on a geodesic.
Finally, theother rotational Killing vector field
a~
gives another constant
of
motion,
(28.99)
which can be interpreted as the angnlar momentnm of the particle. This reduces
to Kepler's second law: Equal areas are swept out in equal times, in the limit of
Newtonian (or weak) gravity. However, in strong gravitational fields, spacetime is
not
Euclidean, and Equation (28.99) cannot be interpreted as "areas swept
out."
Nevertheless, it is interesting that the "form" of Kepler's second law does not
change even in strong fields.
Solving for
i and
<p
from (28.98) and (28.99) and inserting the resultin (28.97),
we obtain
~t2
+
~
(1-
2M)
(L
2
+K)
=
~E2
2 2 r r
2
2
(28.100)
It
follows from this equationthat the radial motion
of
a particle on a geodesic is the
same as that
of
a unit mass particle of energy E
2/2
in ordinary one-dimensional
13Recall
thatthe-l-momentum of specialrelativity is p/k =
mx/.L.

28.6
GENERAL
THEORY
OF
RELATIVITY
927
t
p
Figure 28.3 Theeffective potential
VCr)
for a massiveparticlewith L
2
= 5M
2.
nonrelativistic
mechanics
movingin aneffective
potential
1 2M
(L
2
)
1 M L
2
ML
2
V(r)=-(l--)
-+1<
=-1<-1<-+----.
2 r r
2
2 r 2r
2
r
3
(28.101)
Once we solve Equation (28.100) for the radial motion in this effective potential,
we can find
the angular motion and the time coordinate change from (28.98)
and (28.99). The new feature provided by
GTR
is that in the radial eqnation
of
motion, in addition to the "Newtonianterm"
-I<
M/ r and the "centrifugalbarrier"
L
2
/2r
2
,
we have the new term - ML
2
/
r
3,
which, a small correction for large r,
will dominate over the centrifugal barrierterm for small
r.
Let us consider first the massive particle case, I< = 1.
The
extrema
of
the
effective potential are given by
(28.102)
Thus, if
L
2
< 12M
2
,
no extrema exist (see Fignre 28.3), and a particle heading
toward the center
of
attraction, will fall directly to the Schwarzschild radius r =
2M,
the zero
of
the effective potential, and finally into the spacetime singularity
r =
a.For
L
2
> 12M
2
,
thereadermaycheckthatR+
isantinimumofV(r),
while
R_ is a maximum (Figure 28.4).
It
follows that stable (unstable) circular orbits
exist at the radins
r = R+
(r
= R_). In the Newtonian limit
of
M « L, we get
R+
'"
L
2
/
M, which agrees with the calculation in Newtonian gravity (Problem
28.30). Fnrthermore, Equation (28.102) puts a restriction
of
R+ >
6M
on R+ and
3M < R_ < 6M on
R_.
This places the planets
of
the Sun safely in the region
of
stable circular orbits.

(28.103)
(28.104)
928 28. DIFFERENTIAL
GEOMETRY
If
a massive particleis displacedslightly from its stable equilibriumradius R+,
it will oscillate radially with a frequency w, given b
y
14
W;=d2~1
=M;R+-6~).
dr
,~R+
R+ - 3MR+
On the other hand, the orbital frequency is given by Equation (28.99),
L
2
M
w
2
=_ =
-..,,---~
~
Rt
R~-3MRr
where L
2
has been calculated from (28.102) and inserted in this equation.
In
the
Newtonian limit
of
M « R+, we have
w~
'"
co,
'"
M/
R~.
If
w~
= w" the
particle will return to a given value of
r in exactly one orbital period and the orbit
will close. The difference between
w~
and w, in GTR means that the orbit will
precess at a rate of
w
p
=
w~
- w, = (1 -
w,/w~)w~
=
-[(1
- 6M/R+)1/2 -
l]w~,
which in the lintit
of
M « R+ reduces to
3M
3/2
3(GM)3/2
w
p
'"
R
5
/
2
= 2R
5
/
2'
+ C +
If
we include the eccentricity e and denote the semimajoraxis
of
the ellipticalorbit
by
a, then the formula above becomes (see [Misn 73, p. 1110])
3(GM)3/2
w
p
'"
c
2
(1 _ e
2)a
5
/
2
'
Due to its proxintity to the Sun, Mercury shows the largest precession fre-
quency, which, after taking into account all othereffects such as pertorbations due
to other planets, is 43 seconds of arc per century. This residual precession rate
had been observedprior to the formulation of
GTR
and had been an unexplained
mystery. Its explanation was one of the most dramatic early successes
of
GTR.
We now consider the null geodesics. With K = 0 in Equation (28.101), the
effective potential becomes
L
2
V(r)
= 2r
3
(r - 2M),
which has a maximum at r = R
max
es 3M, as shown in Figure 28.5. It follows
that in GTR, unstable circnlar orbits of photons exist at r = 3M, and that strong
gravity has significant effect on the propagation
of
light.
14In
the
Taylor
expansion of any
potential
VCr)
about
the
equilibrium
position'u of a
particle
(of
writ mass),itis thesecond
derivative
term
that
resembles
Hooke's
potential,
!kx
2
withk = (d
2
V
/dr
2)ro.
28.6
GENERAL
THEORY
OF
RELATIVITY
929
distance from origin, r
--------·1-.-.-.-.-.-.--·---
j.---
------.-.+.
--"---
! .o.
i
.,
.
····T···········
i-
,
,
,
"0"
'_._._--:---".--
!
I
,
,
----_
....
_-_._---
....
1---
i
- ...
_ .
]
--._-_
__
_+.---
~
'"
2M
4M
6M
8M
10M
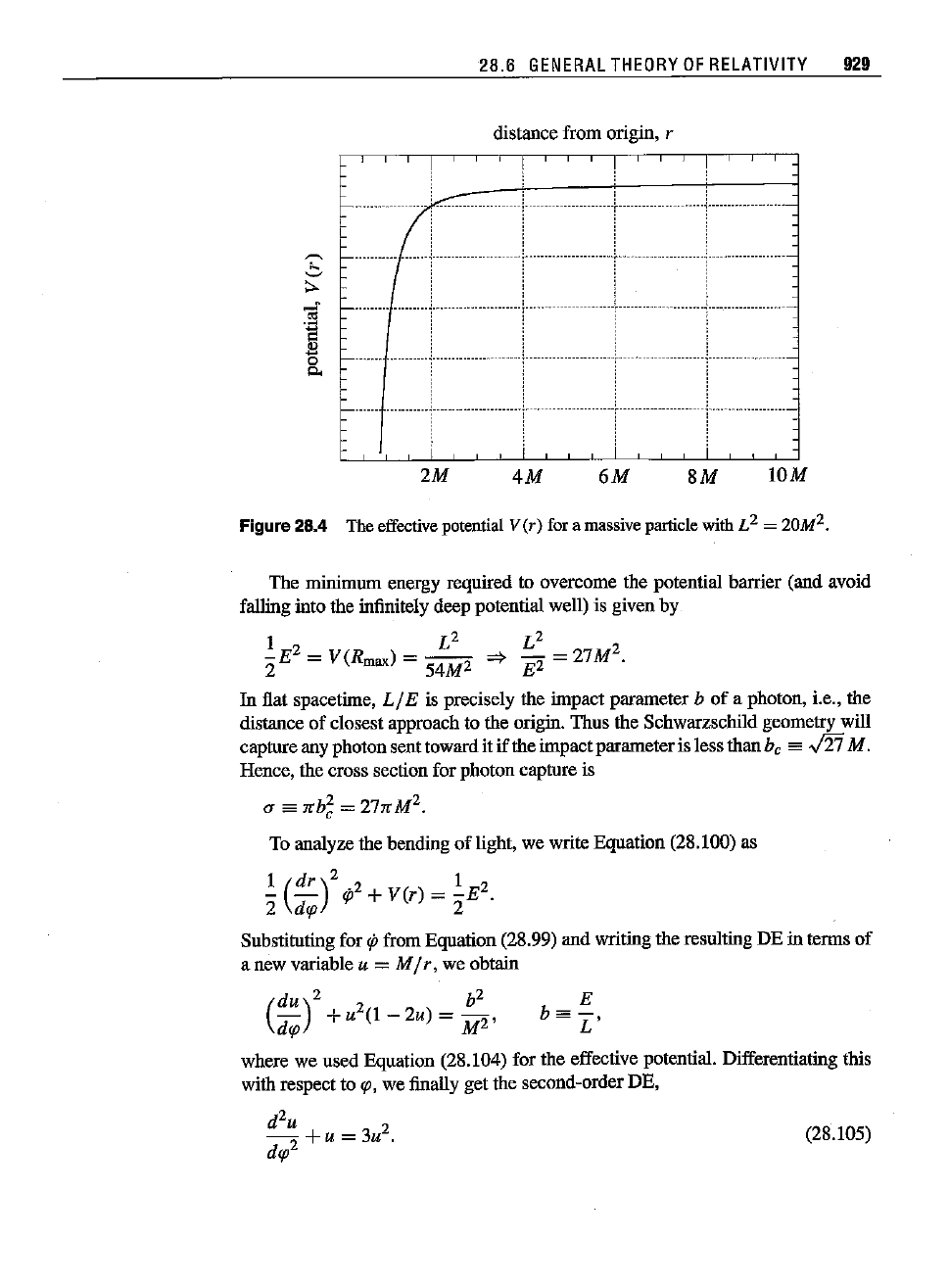
Fi9ure 28.4 Theeffective potentialV(r) fora massiveparticlewith L
2
= 20M
2.
The minimum energy required to overcome the potential barrier (and avoid
falling into the infinitely deep potential well) is given by
1 L
2
L
2
2
E2
=
V(R
max)
= 54M2
=>
E2 =
27M
2.
In
flat spacetime,
L/
E is precisely the impact parameter b
of
a photon, i.e., the
distance of closest approach to the origin. Thus the Schwarzschildgeometry will
captureany photonseuttowardit
if
the impactparameterisless than be es .fYiM.
Hence,thecrosssectionfor
photon
capture
is
a sa
:n:b~
= 27:n:M
2.
To analyze the bending
of
light, we write Equation (28.100) as
~
(dr)2
</,z
+
V(r)
=
~E2.
2 dip 2
Substituting for
rp
from Equation (28.99) and writing the resulting DE in terms of
a new variable
u = M/ r, we obtain
(
dU) 2 b2 E
drp
+u
2(1-2u)
=
M2'
"<t:
where we used Equation (28.104) for the effective potential. Differentiating this
with respect to
rp,
we finally get thesecond-orderDE,
d
2
u
-2
+u = 3u
2
(28.105)
drp
930
28.
DIFFERENTIAL
GEOMETRY
distance from origin,r
f-
..
1\
\
I-
1-
....
i\
..
'\
1-...
i\
f-
....
····-i--··········
r-;
i
,
i i i i
, ,
i
, , ,
i
R
10M
30M
40M
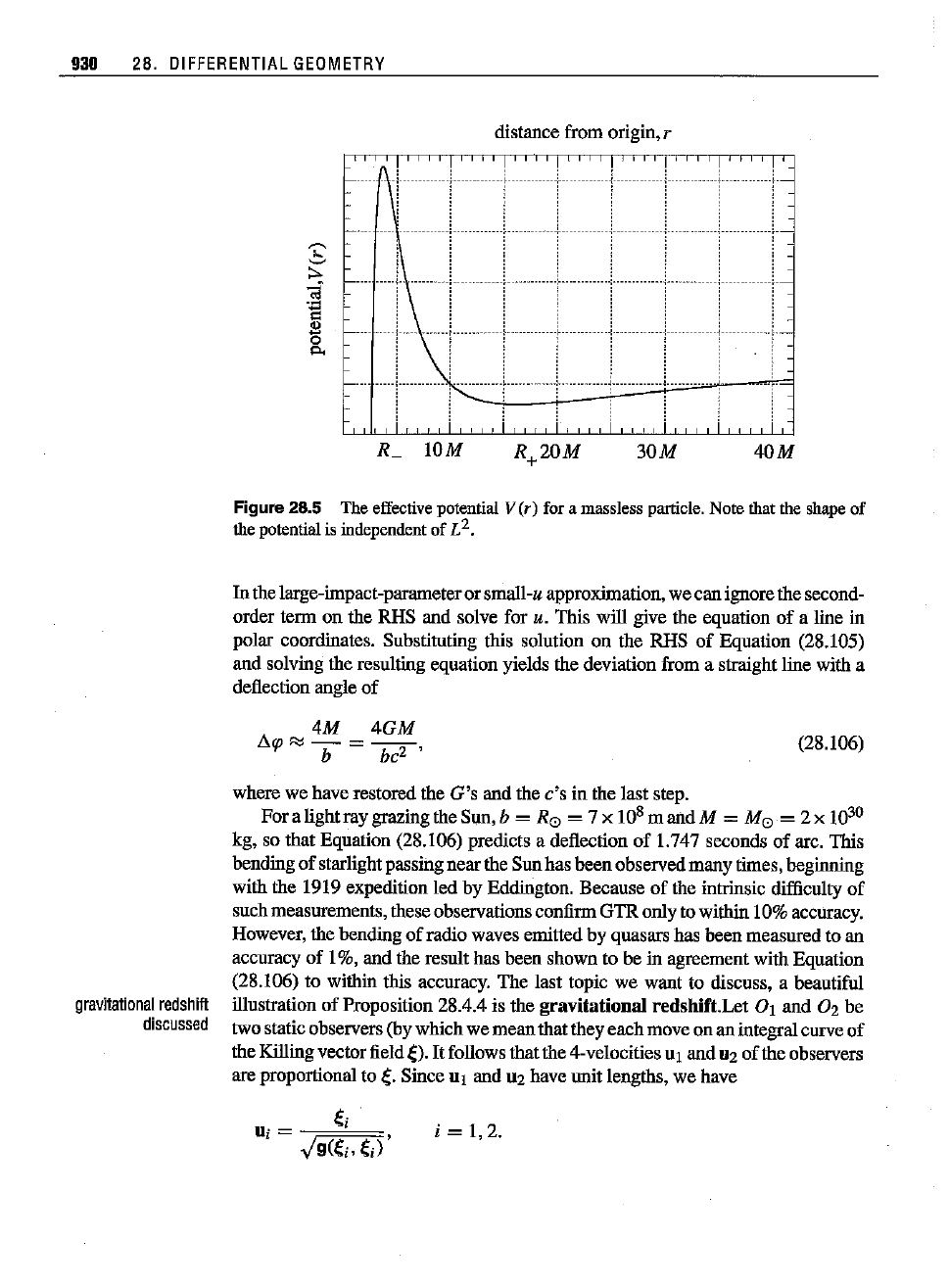
Figure
28.5
The effective potential V
(r)
for a massless particle.Note thatthe shape
of
the
potential
is
independent
of L
2
•
In the large-impact-parameteror small-u approximation, we can ignorethe second-
order term on the RHS and solve for
u. This will give the equation
of
a line in
polar coordinates. Substituting this solution on the
RHS
of
Equation (28.105)
and
solving the resulting equation yields the deviation from a straight line with a
deflection angle
of
4M
4GM
8<p
'"
b = bc2 '
(28.106)
where we have restored the
G's
and the
c's
in the last step.
For
a lightray grazing the Sun, b =
R@
= 7 x lOS
mandM
= M@,=
2x
10
30
kg, so that Equation (28.106) predicts a deflection
of
1.747 seconds
of
arc. This
bending
of
starlightpassingnearthe
Sun
has
been
observedmany times, beginning
with the 1919 expedition
led
by Eddington. Because
of
the intrinsic difficulty
of
such measurements, theseobservations confirm
GTR
oulyto within 10% accuracy.
However, the bending
of
radio waves emitted by quasars has been measured to an
accuracy
of
I%,
and
the result has been shown to be in agreement with Equation
(28.106) to within this accuracy.
The
last topic we want to discuss, a beautiful
gravitational
redshilt
illustration
of
Proposition 28.4.4 is the
gravitational
redshift.Let
01
and
02 be
discussed
two static observers (by whichwe
mean
thatthey
each
move on an integralcurve
of
the Killingvectorfield
e).
It
follows thatthe 4-velocitiesU1
and
U2
of
the observers
are proportional to
e.
Since U1 and U2 have unit lengths, we have
i =
1,2.
28.6
GENERAL
THEORY
OF
RELATIVITY
931
distance from origin, r
. c
ii
!
,
••
000"._
•••
_------,
••
---
••••
.0. j _
i
F--.
...
···············r
+..................
...
,.................
c
E--.
.. . ,..
1-...0.""
..
"\-+
- ;............ .j -"
1-
.....
5M
10M
15M
20M
Figure28.6 A
spacetime
diagram
depicting
theemissionof lightby
observer
01 andits
reception by Oz.
Suppose Oi emits a light beam and Oz receives it (see Figure 28.6). Since light
travels on a geodesic, Proposition 28.4.4 gives
(28.107)
where u is tangent to the light trajectory (or the light signal's 4-velocity). The
frequency
of
light for any observer is the time component of its 4-velocity, and
because the 4-velocity
of
an observerhas the form
(I,
0, 0, 0) in the frame of that
observer,
we can
write
this
invariantly
as
Wi = g(u,
u.)
= g(n,
ei),
i = 1,2.
,,!g(ei'
ei)
In particular, using Equation (28.107), we obtain
1-2M/rz
1-2M/ri'
where we used g(e,
e)
=
gOO
= (I -
2M/r)
for the Schwarzschild spacetime,
and ri and
ri
are the radial coordinates
of
the observers Oi and Oz, respectively.
In terms of wavelengths, we have
1-
2M/,!
1-
2M/rz
(28.108)
It
follows from Equation (28.108) that as light moves toward regions of weak
gravity
(rz >
ri),
the wavelengthincreases ('.Z > AO,i.e., it will be "red-shifted."

932
28.
DIFFERENTIAL
GEOMETRY
this makes sense, because an increase in distance from the center implies an in-
crease
inthe
gravitational
potential
energy.
and,
therefore,
a
decrease
ina
photon
'8
energy luo. Pound and Rebka used the Mossbauer effect in 1960 to measure the
change in the wavelength
of
a
beam
of
lightas it falls downa tower on the surface
of
the Earth. They found that, to within the 1% experimental accuracy, the
GTR
prediction
of
the gravitational redshift was in agreement with their measurement.
28.7 Problems
28.1. Show that
de
= 0 A
(Ge)
- e A
(GO).
28.2.
Let
Aand 8 be matriceswhose elementsare one-forms. Show that (AA
8)'
=
-8'
AA'.
28.3. Write Equation (28.20) in component form
and
derive Equation (28.24).
28.4.
Find
dO
if
0-
( 0
- cot
OeqJ
-cote.~)
o '
where (e, 'P) are coordinates on the unit sphere 8
2
.
28.5.
Find
the curvature
of
the two-dimensional space whose arc length is given
by
ds
2
=
dx
2
+x
2d
y
2.
28.6.
Find
the curvature
of
the three-dimensional space whose arc lengthis given
by
ds
2
=
dx
2
+x
2d
y2 +dz
2
.
28.7.
Find
the curvaturetensors
of
the Friedmann
and
Schwarzschildspaces given
in Example 28.2.3.
28.8. (a) Show that in]R3 the composite operator
do
*gives the curl
of
a vector
whenthevectoris
written
as
components
of a
two-form.
(b) Similarly, show that *0 d is the divergence operator for one-forms.
(c)
Use
these results and the procedure
of
Example 28.2.4 to find expressions for
the curl
and
the divergence
of
a vector in curvilinear coordinates.
28.9.
Let
0 = er, v = eko
and
w =
.j
in (28.34) to arrive at (28.35).
28.10. UsingEquations(28.7) and (28.55) showthat Ris a
tensor
of
type (1, 3).
In
particular, it does
not
differentiate functions that multiply vectors and the
l-form
in its
argument.
28.11. Show that
R(o,
v)w
+R(w,
o)v
+R(v,
w)o
= O.
Hint:
Use
the first property
of
Theorem 28.3.2 to change the vector with respect
to which covariantdifferentiation is being performed.
Then
use the Jacobi identity
for Lie brackets
of
vectors.
