Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


28.5
GEODESIC
DEVIATION
AND
CURVATURE
913
28.5 GeodesicDeviation
and
Curvature
Geodesics are the straight lines of general manifolds on which, for example, free
particles move.
If
u represents the tangent to a given geodesic, one can say that
V.u
= 0 is the equation of motion of a free particle. In flat spaces, the relative
velocity of any pair of free particles will
not
change, so that their relative accelera-
tion is always zero.
In general, however, due to the effects of curvature, we expect
a nonzero acceleration. Let us elaborate on this.
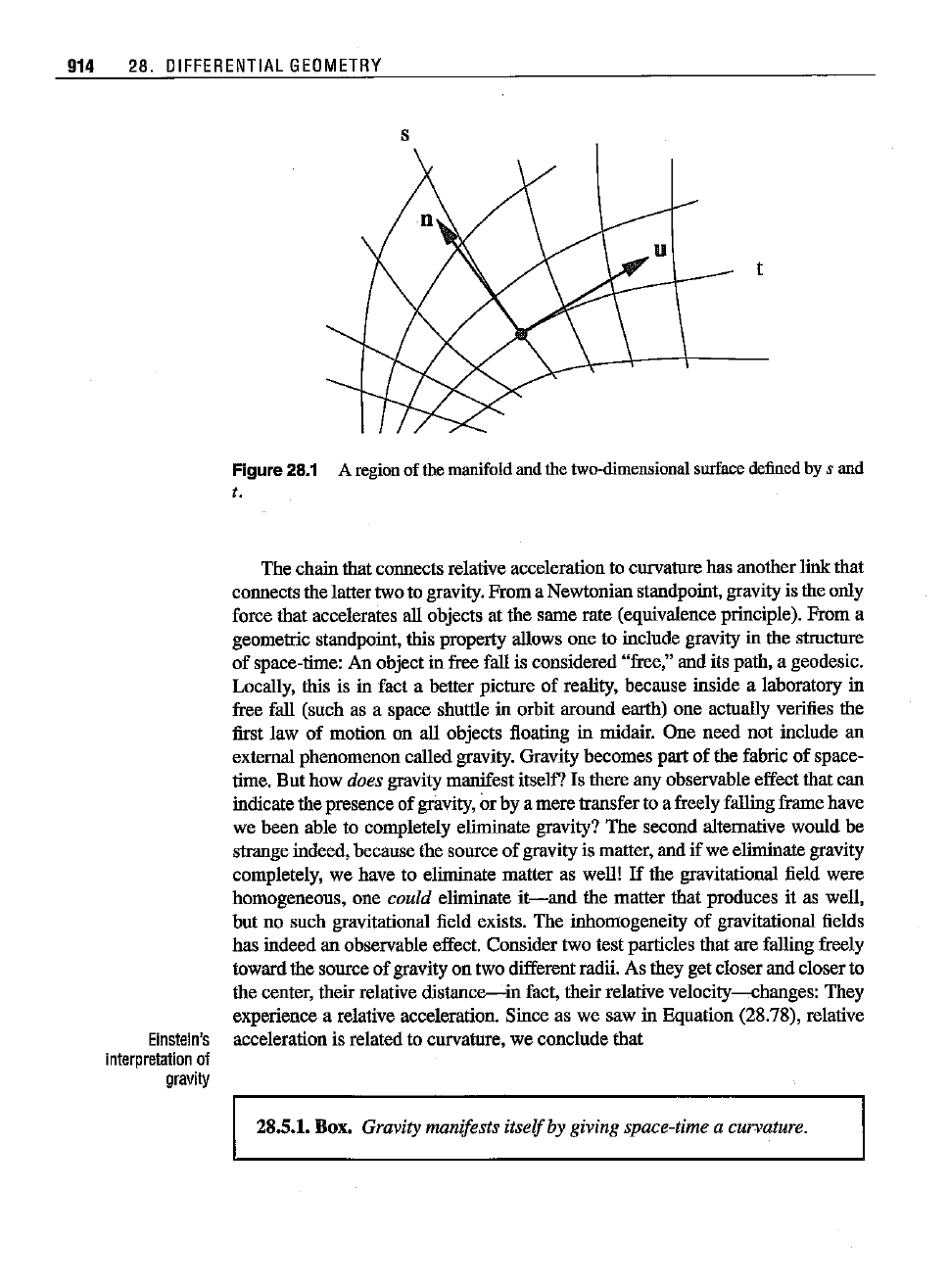
Consider some. region of the manifold through whose points geodesics can
be drawn iu vatious directions. Concentrate on one geodesic and its neighboring
geodesics. Let
t desiguate the parameter that locates points of the geodesic. Let s
be a continuous parameter that labels different geodesics (see Fignre 28.1). One
can connect the points on some neighboring geodesics corresponding to the same
value of
t and obtain a curve paramettized by s. The collection of all geodesics
that pass through
all points of this curve form a two-dimensionalsubmanifoldwith
coordinates
t and s.Each such geodesic is thus described by the geodesic equation
V.u
= 0 with u =
a/at
(because t is a coordinate). Furthermore, as we hop
from one geodesic to its neighbor, the geodesic eqnationdoes not change; i.e., the
geodesic eqnation is independent
of
s. Translated into the langnage
of
calculus,
this means that differentiation
of
the geodesic equation with respect to s will give
zero. Translated into the higher-level language
of
tensor analysis, it means that
covatiant differentiation of the geodesic equation will yield zero. We write this
final translation as
V.(V.u)=
0 where n es
a/as.
This can also be written as
0=
V.
V.u
=
V.
V.u
+
[V.,
V.lu
=
V.(V.n
+[n, uJ) +[V.,
V.Ju,
where we have used the first property of Theorem28.3.2. Using the fact that n and
u are coordinate frames, we conclude that [n, u] = 0 which in conjnnction with
Equation (28.56) yields
V.
V.n
+R(u,
u)u
=
O.
(28.78)
relative
acceleration
equation
of
geodesic
deviation
The firstterm canbe interpretedas the relativeacceleration
oftwo
geodesiccurves
(or free particles), because
V.
is the generalization of the derivative with respect
to t, and
V.n
is interpreted as relative velocity. In a flat manifold, the relative
acceleration for any pair
of
free particles is zero. When curvature is present, it
produces a nonzero relative acceleration.
By writing u =
u' a, and n = n
k
ak and substituting in Equation (28.78), we
arrive at the
equation
of geodesic deviation in coordinate form:
. . k d
2n
m
d . k j dn
k
. . k
u1uJn
Rijk
=
-2-
+-
(ut
n
r"kj)
+U
df'kj
+u1uJn
rnkjr~i'
dt dt t (28.79)
where we have used the fact that
u'a'f
=
df/dt
for any function defined on the
manifold.
914 28.
DIFFERENTIAL
GEOMETRY
s
u
t
Einstein's
interpretation
of
gravity
Figure 28.1 A regionof themanifoldand the two-dimensionalsurfacedefinedby s and
t.
The
chain
that connects relative acceleration to curvatnre has another
link
that
connects
the
lattertwo to gravity.
From
a Newtonian standpoint,gravity is the only
force that accelerates all objects at
the
same rate (equivalence principle).
From
a
geometric standpoint, this property allows one to include gravity in
the
structnre
of
space-time: An objectin free fall is considered "free," and its path, a geodesic.
Locally, this is in fact a better picture
of
reality, because inside a laboratory in
free fall (such as a space shuttle in orbit around earth) one actually verifies
the
first law
of
motion
on all objects floating in midair.
One
need
not
include an
extennal phenomenon called gravity. Gravity
becomes
part
of
the fabric
of
space-
time.
But
how
does gravity manifest itself? Is there any observable effect that
can
indicate
the
presence
of
gravity, or by a
mere
transferto a freely falling frame have
we
been
able to completely eliminate gravity?
The
second alternative
wonld
be
strangeindeed, because the source
of
gravity is matter, and
if
we eliminate gravity
completely, we have to eliminate matter as well!
If
the
gravitational field were
homogeneous, one
could eliminate
it-and
the
matter
that produces it as well,
but
no such gravitational field exists. The inhomogeneity
of
gravitational fields
has
indeed an observable effect. Consider two test particles that are falling freely
toward
the
source
of
gravity
on
two different radii. As they get closer
and
closerto
the center, their relative
distance-in
fact,
their
relative
velocity--changes:
They
experience a relative acceleration. Since as we saw in Equation (28.78), relative
acceleration is related to curvature, we conclude that
28.5.1.
Box. Gravity manifests itselfby giving space-time a curvature.

Riemann
normal
coordinates
28.5
GEODESIC
DEVIATION
AND
CURVATURE
915
This is Einstein's interpretation of gravity. From a Newtonian standpoint, the
relative acceleration is caused by the inhomogeneity of the gravitational field.
Such inhomogeneity (in the field
of
the Moon and the Sun) is responsible for
tidal waves. That is why the curvature term in Equation (28.78) is also called the
tide-producing gravitational force.
28.5.1 RiemannNormal Coordinates
Starting with a point P of an n-dimensional manifold M on which a covariant
derivative
is
defined,
we can
construct
a
unique
geodesicin every
direction,
i.e.,
for every vector in
'Jp(M).
By parallel transportation of the tangent vectors at P,
we can construct a vector field in a neighborhood of P: The value of the vector
field at
Q-assumed
to be close enough to P
-is
the tangent at Q on the geodesic
starting at P and passingthrough
Q.
8
The vectorfield soobtainedmakes it possible
to define an exponential map from the tangent space to the manifold.
In fact, the
integral curve exp(tX) of any tangent vector X in
'Jp
(M)
is simply the geodesic
associated with the vector.
The uniqueness of the geodesics establishes a bijection (in fact, a diffeomor-
phism) betweena neighborhood
of
the origin
of
'J
p(M)
and a neighborhood of P
in M. This diffeomorphism can be used to assign coordinates to all points in the
vicinity of
P. Recall that a coordinate is a smooth bijection from M to
JR".
Now
choose a basis for
'Jp
(M)
and associate the components
of
tX in this basis to the
points on the geodesic exp(tX). Specifically, if
{ai}i~l
are the components of X
in
thechosenbasis,
then
i =
1,2,
...
, n,
are the so-called
Riemann
normalcoordinates (RNes)
of
points on the geodesic
of X. The geodesic equations in these coordinates become
k i . k
r
jia
a!
= 0
=}
r
ji
= 0
because
r~i
is symmetric in i and i-
28.5.2. Proposition. The connection coefficients at a point P E M vanish in the
Riemann
normalcoordinates at P.
Using Equation (28.43), we immediately obtain the following:
28.5.3. Corollary. Let T be a tensor field on M with components TJ:
......
;; with
respect to a Riemann normal coordinate system
{xi}
at P. Then
..
a··
T~l
...': =
_T~l
...
'r.
ll···]s;k
8xk
n.:»
SWe are assuming thatthrough any two neighboring points one can always draw a geodesic. For a proof see [Koba63,
pp. 172-175].

916 28.
DIFFERENTIAL
GEOMETRY
Riemann normal coordinates are very useful in establishing tensor equations.
This is because
28.5.4. Box. Two tensors are identical if
and
only if their components are
the same in any coordinateframe.
F=ma
=}
a=
-V<I>
=}
second
Bianchi
identity
Therefore, to show that two tensors fields are equal, we pick an arbitrary point
in
M,
erect a set of RNCs, and show that the components
of
the tensors are equal.
Sincetheconnection coefficients
vanish
inanRNCsystem,and
covariant
deriva-
tives are the same as ordinary derivatives, tensor manipulations can be simplified
considerably. For example, the components
of
the curvature tensor in RNCs are
i _
ar
i
j l
ar
i
j k
R
jkl
-
-k-
-
-1-'
(28.80)
ax ax
This is not a
tensorrelation-the
RHS is not atensorin ageneralcoordinatesystem.
However,
ifwe
establisharelationinvolvingthe componentsof the curvaturetensor
alone, then that relation will hold in all coordinates, i.e., it is a tensor relation.
For
instance, from the equation above one inunediately obtains
R
i
j kl
+R
i
1j k
+R
i
k1j
=
O.
Since this involves only a tensor, it must hold in all coordinate frames. This is the
Bianchi identity of Equation (28.24).
28.5.5.
Example.
Differentiate Eqnation(28.62) with respect to x
m
and evaluate the
result inRNCto get
Rijkl;m
=
Rijkl,m
=
rijl,km
-
rijk,lm'
From
this
relation
andr
i
"Ik =
ri"1
k'
we obtainthesecond Bianchi identity:
J,
m J ,m
Rijkl;m
+
Rijmk;1
+
Rij1m;k
= 0 and
Rijlkl;m]
=
O.
(28.81)
In
Einstein's
general
relativity,
this
identity
is the
analogue
of Maxwell'spairof homoge-
neonsequations; F.p,y +Fy.,p +Fpy,. =
O.
III
28.5.2 NewtonianGravity
The equivalence principle, relating gravity with the curvature
of
space-time, is
not unique to Einstein. What is unique
to him is combining that principle with
the assumption of
local Lorentz geometry, i.e., local validity
of
special relativity.
Carlanalso used the equivalence principle to reformulate Newtouian gravity in the
language of geometry. Rewrite Newton's second law of motion as
a
2
x
j
a<l>
--+--.
=0,
at
2
ax}

28.5
GEODESIC
DEVIATION
AND
CURVATURE
917
where
4>
is the gravitational potential (potential energy per unit mass). The New-
tonian universal time is a parameter that has two degrees
of
freedom: Its origin
and its unit of measurement are arbitrary. Thus, one can change t to t =
ar
+b
without changing the physics of gravity. Taking this freedom into account, one can
write
(28.82)
Comparingthis with the geodesicequation, we can readoffthe nonzeroconnection
coefficients:
(28.83)
j =
1,2,3.
r
i
OO
=
a4>"
ax
J
Inserting these in Equation (28.62), we find the nonzero components
of
Riemann
curvature
tensor:
(28.84)
, . a
24>
R
J
-
R
J
-
OkO
- -
OOk
-
axiaxk'
Contraction of the two nonzero indices leads to the Laplacian of gravitational
potential
Therefore, the Poisson equation for gravitational potential can be written in terms
of the curvature tensor:
Roo
sa R
i
oiO
= 4rrGp,
Ricci
tensor
defined
where we have introduced the Ricci tensor, defined as
Rik
sa
R~jk'
(28.85)
(28.86)
Equations (28.83), (28.84), and (28.85) plus the law
of
geodesic motion describe
the full content of Newtonian gravitational theory in the geometric language of
tensors.?
It is instructive to discover the relation between curvature and gravity directly
from the equation of geodesic deviation as applied to Newtonian gravity. The
geodesic equation is the equation of motion:
9Theclassicand
comprehensive
bookGravitation, by
Misner,
Thorne,
and
Wheeler,
hasa
thorough
discussionof
Newtonian
gravity
in the
language
of
geometry
in
Chapter
12andis
highly
recommended.

918 28.
DIFFERENTIAL
GEOMETRY
Differentiate this equation with respect to the parameter s,noting that aI
as
nialax
i
:
Now note that
ax
j
las=n
i
ax
j
lax
i
=
nl
. So, we obtain
a
2
n
j
. a
2
<1>
at2
+n'
ax
i
ax
j
=
O.
This is equivalent to Equation (28.78), and one recognizes the second term as the
tide-producing (or the curvature) term.
28.6 GeneralTheory of Relativity
No treatment
of
Riemannian geometry is complete without a discussion of the
general theory of relativity. That is why we shall devote this last section of the
current chapter to a briefexposition of this theory.
Wehave seen that Newtoniangravity can
be translatedinto the language of dif-
ferential geometryby identifyingthe gravitationaltidal effects with the curvature
of
space-time. This straightforward interpretation
of
Newtonian gravity, in particular
the retention
of
the Euclidean metric and the universality of time, leads to no new
physicaleffect. Furthermore, it is inconsistentwith the special theory of relativity,
which mixes space and time coordinates via Lorentz transformations. Einstein's
general theory of relativity (G1R) combines the eqnivalence principle (that freely
falling objects move on geodesics) with the local validity of the special theory
of
relativity (that the metric of space-time reduces to the Lorentz-Minkowski metric
of
the special theory of relativity).
28.6.1 Einstein'sEquation
Since the metric plays a central role in general relativity, let us study its effect on
the curvature tensor. The reader may verify that (Problem 28.23)
0=
R(u,
v)(w·
x) = [R(u, v)w] . x +
w·
[R(u, v)x].
Using this, one can show that
Rijkl
= -
Rjikl'
(28.87)
which is the first equation of (28.23). Equations (28.23) and (28.24) form a com-
plete set of symmetries of the Riemarm curvature tensor. Other symmetries that
follow from them are
Rijkl
=
Rklij
and
R[ijklJ
=
o.
(28.88)

28.6
GENERAL
THEORY
OF
RELATIVITY 919
An important tensor that can be constructed out
of
Riemann curvature tensor
Einstein
tensor and the metrictensoris the
Einstein
tensor
G, which is related to the Ricci tensor
defined in Equation (28.86). To derive the Einsteintensor, first note that the Ricci
tensor is symmetric in its indices (see Problem 28.25):
curvature
scalar
Next, define the
curvature
scalar
as
defined
R
~
R
i
~
gijR"
- i - IJ"
(28.89)
(28.90)
Now, contract
i with m in Equation (28.81) and use the antisymmetry
of
the
Riemarm tensor in its last two indices to obtain
R
i
jkl;i
+R
jk;l
- R
jl;k
=
O.
Finally, contract j and I and use the antisymmetry
of
the Riemarm tensorin its first
as well as its last two indices to get
2R
i
k;i
-
R;k
=0, or
Rjk;i
-
hjkR;i
=
O.
Summarizing the foregoing discussion, we write
V
·G=O,
(28.91)
Karl Schwarzschild
(1873-1916) was the eldest of five sons
andone
daughter
bornto Moses
Martin
Schwarzschild
andhis
wife,
Henrietta
Sabel.
His
father
was a
prosperous
member
of
thebusiness
community
in
Frankfurt,
with
Jewish
forbears
in
that
city
traced
backtothe
sixteenth
century.
From
his
mother,
avivacious, warm
person,
Karl
undoubt-
edlyinheritedhis
happy,
ontgoingpersonality, andfrom his fa-
ther,
acapacityfor
sustained
hard
work.
His
childhood
was
spent
in
comfortable
circumstances
among
alargecircleof
relatives,
whose
interests
included
artand
music;
he wasthe
first
to be-
comeascientist.
After
attending
a
Jewish
primary
school,Schwarzschild
entered
the
municipal
gymna-
siumin
Frankfurt
attheageof eleven.His
curiosity
about
the
heavens
was
first
manifested
then:
Hesavedhis
allowance
andboughtlensestomakeatelescope.
Indulging
this
interest,
his
father
introduced
himtoa
friend,
J.
Epstein,
a
mathematician
whohada
private
obser-
vatory.
With
Epstein's
son
(later
professor
of
mathematics
atthe
University
of
Strasbourg),
Schwarzschild
learned
to useatelescopeand
studied
mathematics
of a
more
advanced
type
than
he was
getting
in school.His
precocious
mastery
of celestial
mechanics
resulted
in
two
papers
on
double
star
orbits,
written
whenhe wasbarelysixteen.
In 1891SchwarzschildbegantwoyearsofstudyattheUniversity ofStrasbonrg,where
Ernst
Becker,
director
of the
observatory,
guidedthe
development
of hisskills in
practical
astronomy-skills
thatlater
wereto
form
asolid
underpinning
forhis
masterful
mathemat-
icalabilities.

920
28.
DIFFERENTIAL
GEOMETRY
At age twentySchwarzschild went to the University
of
Munich. Three years later,
in 1896, he
obtained
his Ph.D., summa cum laude. His
dissertation
was an
application
of
Poincare's
theory
of stable
configurations
in
rotating
bodies to,
several
astronomical
problems,
including tidaldeformationin satellites andthe
validity
of
Laplace's
suggestion
as to how the solarsystem
had
originated.
Before
graduating,
Schwarzschild
also found
time
to do some
practical
workwith
Michelson's
interferometer.
At a meetingof theGermanAstronomicalSocietyin Heidelbergin 1900he discussed
thepossibilitythatspacewas
non-Euclidean.
In thesameyearhepublished a
paper
giving
alowerlimitfor theradiusof curvatureof spaceas 2500lightyears.From 1901until 1909
he was professor at Gottingen, where he collaborated with Klein, Hilbert, and
Minkowski,
puhlishingon electrodynamics andgeometricaloptics.In 1906,he studiedthe transportof
energythrougha starhyradiation.
From
Gcttingenhewentto
Potsdam,
butin 1914he
volunteered
for
military
service. He
served
inBelgium,
France,
and
Russia.
WhileinRussiahe
wrote
two
papers
on
Einstein's
relativity
theory
andoneon
Planck's
quantum
theory.
The
quantum
theory
paper
explained
thatthe Stark effectcouldbe provedfrom thepostulatesof quantumtheory.
Schwarzschild's
relativity
papers
givethe
first
exactsolution
of
Einstein's
general
grav-
itational
equations,
givingan
understanding
of the
geometry
of spacenearapointmass.He
alsomadethe
first
study
of
blackholes,showingthatbodiesofsufficiently
large
masswould
haveanescapevelocityexceedingthespeedof lightandsocouldnotbe seen.
However,
he
contracted
anillnesswhileinRussiaanddiedsoonafter
returning
home.
The
automaticvanishing
of
the divergence
of
the
symmetric
Einsteintensorhas
an importantconsequencein the field equation
of
GTR.
It
is reminiscent
of
a similar
situationin electromagnetism,in whichthe vanishing
of
the divergence
of
the fields
leads to the conservation
of
the electric charge, the source
of
electromagnetic
flelds.l"
Just as Maxwell's equations are a generalization
of
the static electricity
of
Coulombto a dynartrical theory, Einstein's
GTR
is the generalizationofNewtotrian
static gravity to a dynamical theory. As this generalization ought to agree with the
successes
of
the Newtoniangravity, Equation(28.91)
must
agree with(28.85). The
bold
step taken by Einstein was to generalize this relation involving ouly a single
component
of
the Ricci tensor to a full tensor equation.
The
natural tensor to be
used as the source
of
gravitation is the stress
energy
tensor!'
TiL
V
ea (p +
p)uiLUV
+pgiL
V,
or
T = (p +
p)u
181
u +P9,
where the source is treated as a fluid withdensity p, four-velocity u,
and
pressure
p. So, Einstein suggested the equation G = KTas the generalization
of
Newton's
WIt
wasMaxwell's
discovery
of the
inconsistency
of the
pre-Maxwellian
equations
of
electromagnetism
with
charge
conser-
vation
that
prompted
himto
change
notonlythe
fourth
equation
(to maketheentireset of
equations
consistent withthe
charge
conservation),
butalsothe
course
ofhuman
history.
11
In
GTR,
itis
customary
tousethe
convention
that
Greek
indicesrunfrom0 to 3,i.e., they
include
bothspaceandtime,while
Latin
indices
encompass
onlythespace
components.

28.6
GENERAL THEORY OF RELATIVITY
921
universal law
of
gravitation. Note that V . G = 0 automatically guarantees mass-
energy conservation
as in Maxwell's theory
of
electromagnetism. Problem 28.27
calculates
K to be 8". in units in whichthe universal gravitational constant and the
speed
of
light are set equal to unity. We therefore have
Einstein's
equation
of
the
general
theory
of
relativity
G=8".T,
or
R -
!Rg
=
8".[(p
+
p)u
® u +
pg].
(28.92)
cosmological
constant
This is
Einstein's
equation
of
the general theory
of
relativity.
The
Einstein tensor G is nearly the only symmetric second-rank tensor made
out
of
the Riemann and metric tensors that is divergence free.
The
only other
tensor with the same properties is
G+Ag, where A is the so-called cosmological
constant
(see Problem 28.28). When in 1917, Einstein applied his GTR to the
universe itself, he found that the universe ought to be expanding. Being a
fum
believer in Natore, he changed his equation to G +Ag = 8".T to suppress the
unobservedprediction
of
the expansion
of
the universe. Later, when the expansion
was observed by Hubble, Einstein referred to this mutilation
of
his
GTR
as
"the
biggest blunder
of
my life."
AleksandrAleksandrovich
Friedmann
(1888-1925)wasbom
intoamusicalfamily-his
father,
Aleksandr
Friedmann,
being
a
composer
andhis
mother,
Ludmila
Vojacka,
the
daughter
of
the
Czech
composer
Hynek
Vojacek.
In
1906 Friedmann graduated from the gymnasium with
the gold medaland
immediately
enrolled in the
mathematics
section
of the
department
of
physics
and
mathematics
of St.
Petersburg
University.
Whilestilla
student,
he
wrote
anumber
of
unpublished
scientific
papers,
oneofwhichwas
awarded
agold
medalby the
department.
After
graduation
fromthe
university
in 1910,
Friedmann
was
retained
in the
department
to
prepare
fortheteachingprofession.
In
thefall of
1914,
Friedmann
volunteered
for servicein an
aviation
detaclunent,
in
whichhe
worked,
first
onthe
northern
front
andlateron
other
fronts,
to
organize
aerologic
and
aeronavigational
services. Whileatthe
front,
Friedmann
often
participated
inmilitary
flights
as an
aircraft
observer.
In the
summer
of 1917he was
appointed
asectionchiefin
Russia's
first
factory
forthe
manufacture
of
measuring
instruments
usedin
aviation;'
helater
became
director
of the
factory.
Friedmann
hadto
relinquish
thispostbecause
of
theonset
of
heart
disease.
From
1918 until 1920, he wasprofessor in the
department
of theoretical
mechanics
of
Perm
University.
In 1920he
returned
to
Petrograd
and
worked
atthemainphysics
observatory
of the
Academy
ofSciences,
first
asheadof the
mathematics
department
and
later,
shortly
before
his
death,
as
director
of the
observatory.
Friedmann's
scientific
activity
was
concentrated
in the
areas
of
theoretical
meteorology and
hydromechanics,
where
he
demonstrated
his
mathematical
talent
andhis
unwavering
strife
for,
andabilityto
attain,
the
concrete,
practical
application
of solutions to
theoretical
problems.
Friedmann
madea
valuable
contribution
to
Einstein's
general
theory
of
relativity.
As
always,
his
interest
was not limitedsimply to
familiarizing
himselfwith this new field

922
28.
DIFFERENTIAL
GEOMETRY
of sciencebutled to his own
remarkable
investigations.
Friedmann's
work
on the
theory
of
relativity
dealtwiththecosmological
problem.
In his
paper
"tiberdie
Kriimmung
des
Raumes"
(1922), he outlined the
fundamental
ideas of his cosmology: the supposition
concerning the homogeneity of the
distribution
of
matter
in space and the consequent
homogeneity and
isotropy
of
space-time.
This
theory
is especially
important
because
it
leads to a sufficiently
correct
explanation of the
fundamental
phenomenon knownas the
"red
shift."
Einstein
himself
thought
that
thecosmologicalsolution to the
equations
of a
fieldhadtobe
static
andhadtoleadtoaclosedmodelofthe
universe.
Friedmann
discarded
both
conditions
andanivedatan independent
solution.
Friedmann's
interest
in the
theory
of
relativity
was by no
means
a passing
fancy.
In
the last
years
of his life,
together
withV.K.
Frederiks,
he beganworkon a
multivolume
textonmodem
physics.
The
first
book,The World as Space and Time, is
devoted
to the
theory
of
relativity,
knowledge
of which
Friedmann
considered
oneof the
cornerstones
of
an
education
inphysics.
In
addition
tohisscientific
work,
Friedmann
taught
courses
inhigher
mathematics
and
theoretical
mechanics
at
various
colleges in
Petrograd.
He
found
timeto
create
new
and
original
courses,
brilliant
in
their
form
andexceedingly
varied
intheir
content.
Friedmann's
unique
coursein
theoretical
mechanics
combined
mathematical
precision andlogicalcon-
tinuity
with
original
procedural
andphysical
trends.
Friedmanndiedoftyphoidfeverattheageofthirty-seven.
In
1931,hewasposthumously
awarded
theLeninPrizeforhis
outstanding
scientific
work.
28.6.2 Static Spherically Symmetric Solutions
The general theory of relativity as given in Equation (28.92) has been strikingly
successful in predicting the spacetime-? structure of our universe.
It
predicts the
expansion
of
the universe, and by time-reversed extrapolation, the big bang cos-
mology; it predicts the existence
of
blackholes and other final products of stellar
collapse; and on a less grandiose scale, it explains the small precession of Mer-
cury, the bending of lightin the gravitational field of the Sun, and the gravitational
redshift. We shall not discuss the solution
of
Einstein's equation in any detail.
However, due to its simplicity and its use of geometric arguments, we shall con-
sider the solution to Einstein's equation exterior to a static spherically symmetric
distribution of mass.
Let us firsttranslatethe two adjectives used in the lastsentenceinto a geometric
language. Take static first. We call a phenomenon "static" if at different instants
it "looks the same."
ThUS,
a static solution of Einstein's equation is a spacetime
manifoldthat "looks the same"for all time.
In the language
of
geometry"looks the
same"
meansisometric, because metricis the essence
of
the geometryof space-
time. InEuclideanphysics,time can be thought
of
as an axis ateach point(moment)
12The
reader
maybe
surprised
toseethetwo
words
"space"
and"time"juxtaposed withno
hyphen;
butthisiscommon
practice
in
relativity.
