Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


28.2
RIEMANNIAN
MANIFOLDS
893
Weuse thisequationtofindtheLaplacianin termsof
Ql,
Q2. andq3:
Differentiating once more, we
get
(28.30)
Since {e
1,
e
2,
e
3}
are orthonormal one-forms (as are {dx, dy, dz}), the volume elements
e
1
A
e
2
A
e
3
and
dx /\ dy /\ dz are equal. Thus, we substitute the latter for
the
former in
(28.30), compare with (28.29), and conclude that
"12
r-
_1_
[...!..
(h2h3!L)
+...!..
(hlh3!L)
+...!..
(hlh2
at)]
- hlh2h3 aql
hi
aql aq2 h2 aq2 aq3 h3 aq3 '
which is the result obtained in curvilinearvector analysis.
28.2.5.
Example.
Let M = R
2,
and suppose that the arc length is given by ds
2
=
(dx
2
+d
y2)j
y
2 We can write the metric as 9 =.1
18>.1
+
.218>.2
if
we define
I dx
€
=-
Y
and
2 dy
e=-
y
The dual vectors {e
1,
e
2}
are orthonormal one-forms and G = 1, so we need not worry
aboutraising and loweringindices. Inspection
of
the
definition
of
(3.1
and
e
l,
along withthe
fact that
dx(a
x
)
= dy(a
y)
= I and
dx(a
y)
= dy(a
x
)
= 0, immediately gives
ej
= ya
x
and
ej
= yay.
To find the curvature tensor, we take the exterior derivative
of
the e
i
's:
1
(I)
I I 2
d.
= d
ydx
= - y2dY
rvdx
=.
A. ,
(28.31)
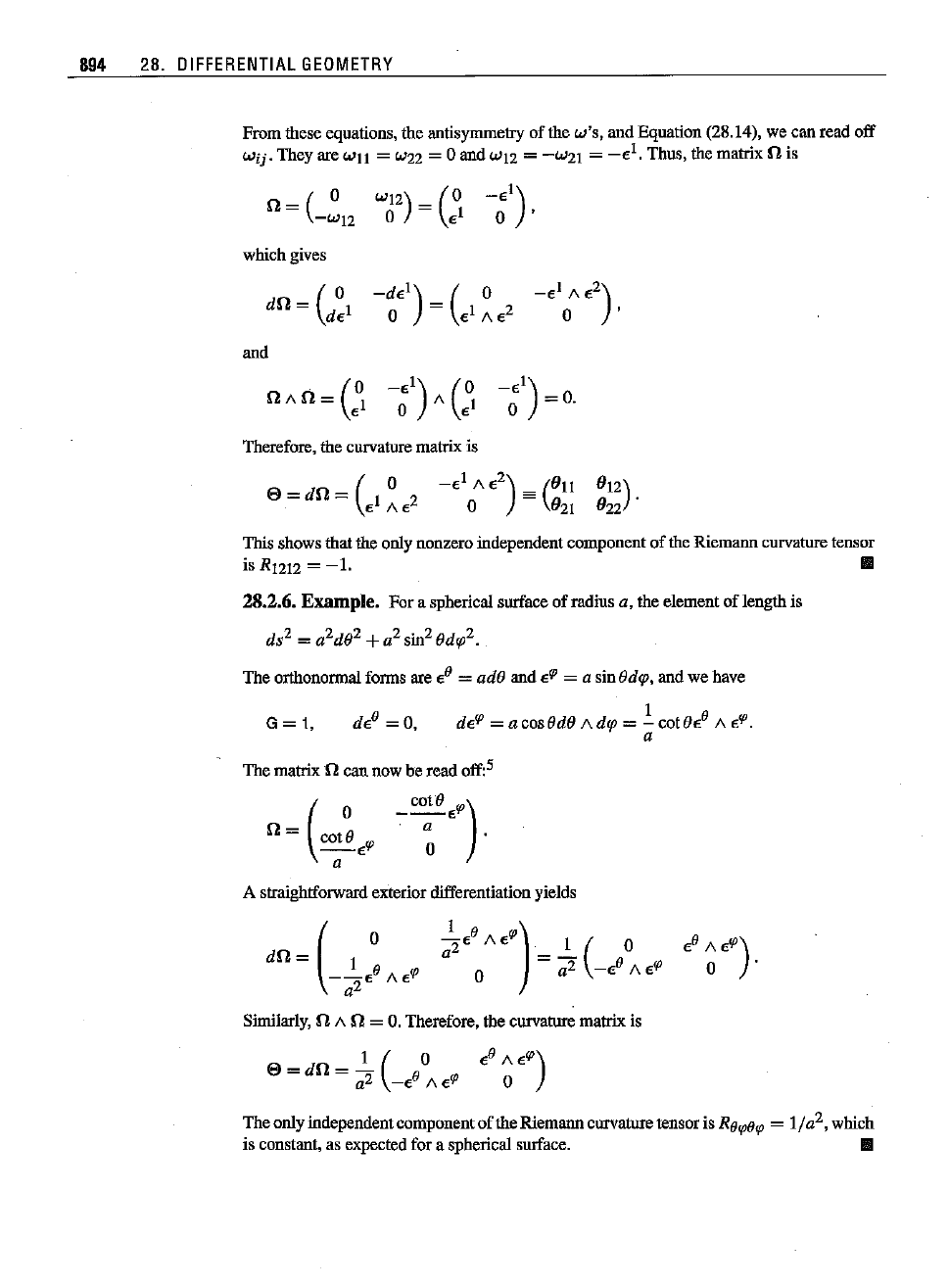
894 28.
DIFFERENTIAL
GEOMETRY
From these equations, the antisymmetry of the w's, and Equation (28.14), we can read off
Wij.
They are
Wl1
= W22 =
Oandw12
=
-W21
=
_e
1.
Thus,
thematrixOis
0-
( 0
-W12
whichgives
W
1
Z)
=
(0
o e
1
_e
1
)
o '
dO=
C~1
and
OAO=
(~1
-n
A
(~
-n
=0.
Therefore,
the
curvature
matrix
is
e=dO=(
1
0
Z
e
Ae
Thisshowsthattheonlynonzeroindependent componentof theRiemann
curvature
tensor
isRl2lZ=-1.
l1li
28.2.6. Example. Fora
spherical
surface
of
radius
a, the
element
of
length
is
ds
Z
=
aZdO
Z
+a
Z
sin
Z
OdrpZ.
Theorthonormal forms
are
e(}
= ade and
erp
= a sin
Bdep,
and
wehave
G = 1,
1
derp
= a
cos
9dfJ
A
dcp
= - cot
Be()
A
e'P.
a
The
matrix
n cannowbe
read
off:
5
0=
(
cot~
e~
-
c~o
e}
a
A
straightforward
exterior
differentiation
yields
(
0
dO=
1
--e(}
Aerp
a
Z
Similarly, 0 A 0 =
O.
Therefore, the curvature matrix is
e =zn =
~
(0
e
8
A
O
e~)
a2 _,/J1\
erp
Theonly
independent
component
ofthe
Riemann
curvature
tensor
is
R(Jrp(Jtp
= 1/a
2
,
which
is
constant,
as
expected
fora
spherical
surface. II

What
isa
flat
manifold?
28.2
RIEMANNIAN
MANIFOLOS
895
It
is clearthatwhenthe
gij
in the expressionfor the line elementare all constants
for all pointsin the manifold,then
e
i
will be proportionalto
dx'
and
de
i
= 0, for all
i. Thisimmediately tells us that n = 0, aridtherefore e = 0; thatis, the manifold
has no curvature. We call such a manifoldflat. Thus, for
ds
2
= dx
2
+d
y
2 +dz
2
,
the space is flat. However, arc lengths
of
a flat space
come
in various guises with
nontrivial coefficients. Does the curvature
matrix
e recognize the flat arc length,
or is it possibleto fool it intobelieving thatit is privilegedwitha curvaturewhenin
reality the curvatore is still zero?
The
following example shows that the curvatore
matrix can detect flatoess no matter how disguised the line elementis!
28.2.7.
Example.
In sphericalcoordinates,the tine element(arc length)of the lIatEn-
clidean space
R'
is ds
2
=
dr
2
+r
2
de
2
+r
2
8in
2
Bd<p2.
Tocalculate the curvaturematrix,
we first
need
an orthonormal set
of
one-forms, These are immediately obtained from the
expression
above:
e
r
= dr,
eO
=rde. e({J = r sin
Bdcp,
G = 1.
Taking the exterior derivatives
of
these one-forms, we obtain
de" = d
2
r = 0,
d€9 = d(rdO) = dr 1\dO
+r
d
20
= €r 1\
(€9)
=
~€r
1\
€9,
___
r r
~O
d€~
=
d(rsinO)
I\drp =sinOdr 1\
drp+rcosOdO
I\drp
=sin8e
r
A(~)+rcose(€9)1\(
€~O)
rsmfJ
r
rsm
I cotO 9
=
_e
r
Ae({J +
--e
Aef{J.
r r
We can now use Equation (28.14) to find the matrix
of
one-forms n.
In
calculating the
elements
of
fl, we remember that it is a skew-symmetric matrix, so all diagonal elements
are zero. We also note that
de
k
= 0 does IWt imply that
J'j
= O.Keeping these facts in
mind, we can easily obtain
n (the calculation is left as a problem for the reader):
I 9
--€
r
o
cot e
erp
r
The exterior derivative of this matrix is found to be
C.otO
9
.oj
---E
Ae
T
[2
_E
9
A
eqJ
2 '
r
o
SNote that dE(} = 0 does not imply W12 = O.

896 28. DIFFERENTIAL
GEOMETRY
whichis
precisely
(the
negative
of) the
exterior
product
n A
fl,
asthe
reader
maywishto
verify.
Thus,e =dn+
nAn
=0, andthe spaceis indeed
fiat!
III
In
all the foregoing examples, the curvatnre was calculated intrinsically. We
neverhadtoleavethespaceandgo to a higherdimension to
"see"
the
curvature.
For example, in the case of the sphere, the only information we had was the line
element in terms
of
the coordinates on the sphere. We never had to resort to any
three-dimensional analysis to discover a globe embedded in the Euclidean
IR
3.
As
mentioned
earlier,
if
aspacehaslineelements with
constant
gi
j,
then
the
Riemann
curvature vanishes trivially. Wehave also seen examples in which the components
of a metric tensor were by no means trivial, but
e was smart enough to detect the
flatness in disguise. Under what conditions can we choose coordinate systems in
terms of which the line elements have
gij = ±8ij? To answer this question we
need the following lemma (proved in [Flan 89, pp.
135-136]):
28.2.8.
Lemma.
If
0 is a matrix
of
i-formssuch that
dO
+0 /\ (GO) = 0, then
there exists an orthogonal matrix
Asuch that dA = AGO.
The questionraised above is intimatelyrelatedto the connectionbetweencoor-
dinate and orthonormal frames. We have seen the usefulness of both. Coordinate
frames, due to the existence of the related coordinate
functions, are useful for
many analytical calculations, for example in Hamiltoniandynamics. Orthonormal
frames are useful because of the simplicity of expressions inherentin all orthonor-
mal vectors. Furthermore, we saw how curvatnre was easily calcnlated once we
constructed orthonormal dual frames. Naturally, we would like to have both. Is
it possible to construct frames that are both coordinate and orthonormal? The
following theorem answers this question:
28.2.9.
Theorem.
Let M be a Riemannian manifold. Then M is flat, i.e., e = 0
if
and only
if
there exists a local coordinate system {xi} for which
{ail
is an
orthonormal basis.
Proof
The existence of orthonormal coordinate frames implies that {dxi} are
orthonormal. Thus, we can use them to find the curvature. But since
d(dx
i)
= 0
for all
i, it follows from Equation(28.12) that w
i
j
=
OandO
=
O.
So the curvature
must vanish. Conversely, suppose that e =
O.
Then by Lemma28.2.8, there exists
an orthogonalmatrix Asuch that
dA = AGO.Now we define the one-formcolunm
matrix
T by T = Ae, where e is the one-form colunm matrix of Equation (28.14).
. Then, using (28.19), we have
dT
= d(Ae) = dA A e +Ado = (AGO) /\ 0 - A(GO /\
0)
=
o.
Thus,
dT
i
= 0 for all i,
By
Theorem 26.5.14 there must exist zero-forms (func-
tions)
xi such that T
i
=
dx',
These xi are the coordinates we are after. The basis
{ail
is obtained using the inverse
of
A (see the discussion following Proposition
25.1.1). Since Ais orthogonal, both
{dxi} and {ail are orthononnal bases. D

28.3
COVARIANT
DERIVATIVE
AND
GEODESICS
897
28.3 Covariant Derivative
and
Geodesics
The
essence
of
all geometries are straight lines.
The
familiar Euclidean geometry
is developedentirely basedon a number
of
postulatesconcerning certain attributes
and properties for straight lines. From the physical standpoint, straight lines are
those trajectories on which "free"
particles-including
light-travel.
If
geometry
is the basis
of
physical theories (generaltheory
of
relativity, and, to a lesserdegree,
electromagnetism and the nuclear interactions), knowledge
of
straight lines will
be crucial.
28.3.1 Covariant Derivative
Straightlines are characterizedby the "leastamount
of
bending."
In
flat space, this
involves zero bending; but if space is curved, the bending cannot be eliminated.
The
bending
of
space is gauged by a test vector as it moves (infinitesimally) along
some trajectory. The infinitesimal character
of
any trajectory is encapsulatedin the
vector tangent to it at the point
of
interest. Thus the concept
of
straight line is tied
to the way
one
vector (the test vector) changes along a second vector (the tangent
vector).
covariant
derivative
28.3.1. Definition. Let u, v E
X(M)
be vectorfields on M. The covariantderiva-
ofa
vector
tive
ofv
with respect to (or along) u, denoted by V
u
v, is defined as
Vuv = (dv,
u).
So, V
u
:
X(M)
-+
X(M),
i.e., V
u
maps vectorfields to vector fields.
(28.32)
Certain properties
of
the covariant derivative follow from this definition. In
mostbooks on differential geometryand relativity, these properties are used to
de-
fine
the covariant derivative. We collectthese properties in the following theorem.
28.3.2.
Theorem.
Let u, v, and w be vector fields,
and
f and h functions on a
Properties
of manifold M. Then the covariant derivative has thefollowing properties:
covariant
derivative
1. Vuv - Vvu = [u, v].
2.
Vu(fv)
=
u(f)v
+
fVuv.
4. Vju+hw(V) =
fVuv+
hVwv.
Proof
We shall prove the first property, whichhappens to be the hardest. The rest
are easy consequences
of
the definition and the linearity
of
pairing. To prove the
first property, choose a basis" {e.} and its dual
{Ei}
and write v =
viei'
u =
uiei,
6Eventually, we shall takethe basis to be a coordinate frame. But for notational convenience, we first work in a general basis.

898 28.
DIFFERENTIAL
GEOMETRY
and
Then we have
(dv, n)
=(dv
i,
n) ei +vi (dei, u) =
[u(vi)]ei
+
viu
j
(dei,
ej)
,
(du, v) = (du
i,
v) ei +u
i
(de;, v) =
[v(ui)]ei
+u
i
v
j
(dei,
ej)
,
and
(dv, u) -
(du,
v) = [u(v
i)
-
v(ui)]ei
+
viu
j
«dei,
ej)
-
(dej,
ei»'
(28.33)
Let
us evaluate the term in parentheses. Using Equation (28.8), we have
(dei,
ej)
-
(dej,
ei) = (ek®
d'i'
ej)
- (ek® Wkj,ei)
= ek
(w~,
ej
) - ek(w
k
j
,e.) = ek
(r~j
- r
k
j
i).
Thebasischosen
above
was
general.
However,
wearefreetochooseany
convenient
basis to prove a vector
or
tensoridentity.
If
we choose the basis to be a coordinate
frame, then by Equation (28.16),
r~j
- r
k
j i
=
O.
Furthermore,
[u(v
i
) -
v(ui)]ei = [u, v] in a coordinate frame.
Substitutiogthese two relations in Equation (28.33), we obtain the first part
of
the
theorem. D
Tullio Levi-Civila (1873-1941), the son of Giacomo Levi-
Civita, a lawyer who from 1908 was a
senator.
was an out-
standingstudentattheliceoinPadna.101890 heenrolledin the
Facultyof Mathematics of the University of Padua.
Giuseppe
Veronese
and
Gregorio
Ricci-Curbastro
wereamonghis
teachers.
Hereceivedhis diplomain 1894 and in 1895 becameresident
professor
atthe
teachers'
college
annexed
tothe
Faculty
of Sci-
ence at
Pavia.
From
1897 to 1918
Levi-Civita
taught
rational
mechanics
atthe
University
of
Padua. His
years
in
Padua
(where
in 1914he
married
a
pupil,
Libera
Trevisani)werescientifically
themost
fruitful
ofhis
career.
In 1918he
became
professor
of
higher
analysis
at
Rome
and,
in 1920,of
rational
mechanics.
In 1938,
struck
by thefascistracial laws
against
Jews,he
was
forced
togiveup
teaching.
The breadth of his scientific interests, his scruples regardingthe fulfillment of his
academic
responsibilities,
and
hisaffection foryoungpeoplemade Levi-Civita the
leader
of a
flourishing
schoolof
mathematicians.

28.3
COVARIANT
DERIVATIVE
AND
GEODESICS
899
Levi-Civita's
approximately
200
memoirs
in pureand
applied
mathematics
dealwith
analytical
mechanics, celestial
mechanics,
hydrodynamics,
elasticity,
electromagnetism,
andatomicphysics.Hismost
important
contribution
to sciencewasrootedin the
memoir
"Sulle
trasformazioni
delleequazioni
dinamiche"
(1896), whichwas
characterized
by the
use of the
methods
of
absolute
differential
calculusthatRiccihadappliedonlyto
differen-
tial
geometry.
Inthe
"Methodes
decalculdifferentiel
absolus
et
leurs
applications,"
written
withRicciand
published
in 1900inMathematische Annalen,
there
is a
complete
exposition
of thenewcalculus, whichconsistsof a
particular
algorithm
designedtoexpressgeomet-
ricand
physical laws in
Euclidean
andnon-Euclidean spaces,
particularly
in
Riemannian
curved
spaces. The
memoir
concerns
a very generalbut
laborious
type of
calculus
that
made
it possibletodealwithmany
difficult
problems.
including,
according
to
Einstein,
the
formulation of the
general
theory
of
relativity.
Although
Levi-Civita hadexpressed
certain
reservations
concerning
relativity
in the
first
years
after
its formulation (1905), he
gradually
came to acceptthe new views.His
own
original
research
culminated
in 1917 in the
introduction
of the conceptof parallel
transport in
curved
spaces.
With
thisnew concept,
absolute
differential
calculus, having
absorbed
other
techniques.
became
tensor
calculus, now the essential
instrument
of the
unitary
relativistic
theories
of
gravitation
andelectromagnetism.
Inhis
memoirs
of 1903-1916Levi-Civita
contributed
tocelestialmechanics inthestudy
of the
three-body
problem:
thedeterminationof themotionof
three
bodies,
considered
as
reduced
to
their
centers
of massand
subject
to
mutual
Newtonian
attraction.
In 1914-1916
hesucceededineliminating the
singularities
present
atthepointsofpossiblecollisions.past
or
future.
His
research
in
relativity
ledLevi-Civita to
mathematical
problems
suggested
by
atomicphysics,whichinthe 1920swasdeveloping outsidethe
traditional
framework:
the
general
theory
of
adiabatic
invariants,
themotionof abodyof
variable
mass,the
extension
of theMaxwellian
distribution
toa systemof corpuscles, andthe
SchrOdinger
equation.
The covariant differentiation of vectors can be extended to arbitrary tensors
once it is defined for l-forms. For this, we make the extra assumption that V
u
can
be "pushed" inside a pairing, and that when acting on a tensor product, it obeys
the product rule
of
differentiation, i.e., V
u
acts as a derivation on the algebra
of
tensors. Let w be a I-form and v a vector. Then
V
u
(w, v) = (Vuw, v) +(w, V
u
v)
(28.34)
defines the covariantderivative
of
w.Using Equation(28.34) the readermay readily
show the primary covariant derivative relation:
(28.35)
Since an arbitrary tensor of a given kind
can
be expressed as a linear combination
of tensor product of vectors and l-forms, our knowledge of the action of V
u
on functions (coefficients of expansion), vectors, and l-forms, plus the assumed
derivation property of Vu, is enough to uniquely define the action
of
V
u
on any
tensor. Equation(28.34) shows that the covariantderivative ofa l-formwith respect

gOO
28. DIFFERENTIAL
GEOMETRY
to a vector is another I-form, because when it pairs up with a vector it gives a
number. We have already pointed
out
that the covariant derivative of a vector with
respect to another vector is a third vector. We therefore conclude that
28.3.3.
Box.
The covariantderivative
of
a tensor
of
a given kind is another
tensor
of
the same kind.
28.3.4.
Example. Using the definition of the covariant derivative, the reader
may
check
that
Note
thechange in
order
of
indices! (28.36)
Now consider two bases
Ier}
and
{eil}. Write the
primed
basis in terms
of
the other: ei' =
RJ;,ej.
Then
~
. I .
ek,r
i']'
==
Vej'ei' = VRI.,el (RJi,ej) = R
pV
el
(RJj,ej)
J
=
Rip
(Rj'f
V"
(ej)
+V"
(R~f)
ej
I
=
Rlj'R~,emrjl
+R
1
l' el
(Ri,)
em.
'-,-'
=R~"l
Writing ek' =Ric/emon the
LHS,
equating the components on
both
sides,
and
multiplying
both
sides by the inverse
of
the transformation
matrix
R, we obtain
Connection
coefficients
are
not
tensors!
r
'"
Rkf R
I
R
j
r
m
+R
kf
R
1
R
m
i'i' = m i' i'
jl
m
j'
1',1'
--,,-
how a (1, 2)-tensor nontensorial
transforms term
(28.37)
(28.38)
where
Rk~
ea (R-1)k1m'
Equation
(28.37) shows
that
the connection coefficients
aTe
not
tensors.
II
28.3.5.
Example.
Equation(28.36)connects r
i
jk
with the structureconstants of the Lie
algebra
of
vector fields on a manifold. To see this connection, use
the
first property
of
the
covariantderivative in
Theorem
28.3.2
and
Equation (28.36) to obtain
lei.
ejl
= Veiej - Vejei = ek (r
k
j i
-
r~j).
It
follows
from
this equation
that
C~j
= r
k
j i
-
r~j'
In
particular, in a coordinate frame,
C~j
= 0
and
the
connection coefficients are symmetric
in their lower indices, a result we obtained earlier. II

28.3
COVARIANT
DERIVATIVE
AND
GEODESICS
901
Let Tbe atensorof type (r, s).
It
is convenienttothink of V
u
Tas the contraction
of
another tensor S
'"
VT with n. Then V may naturally be treated as a linear
operatorthatmaps
TJ
(M),
the bundleoftensorfieldsoftype(r, s), to TJ+!
(M),
the
bundle
of
tensor fields
of
type (r, s +I). One then writes V : TJ
(M)
--->
T;+l
(M)
gradient
operator
for
and calls V the generalized
gradient
operator.
If
tensors
then
and,
withu = ukek,
V
u
T=
T~l
..
':
ukej ®
...
@ej
®
eit
®
...
® e
is
.
ll
...
]s,k
1 r
(28.39)
(28.40)
Using these relations, we can calculate the components of the covariantderivative
of
a general teosor.
It
is clear that
if
we use ek instead
of
u, we obtain the kth
component
of the
covariant
derivative.
So, ontheone
hand,
we have
(28.41)
and on the other hand,
V T = V (Til"'" e·
<81
•••
<81
e·
<81
€iI
<81
•••
<81
€J,)
ek ek
It
...
}s
'1 lr
=
T~l
'r keil ®
...
® ej ® e
it
®
...
® e
is
It
ls,
T
r
+
T;11
......
~:
L eit ®
...
® Vekeim ®
..
.CiT ® e
it
®
...
® e
is
m=l
~
enr imk
s
+
T~l
'r
'"""
ej ®
...
®ej
® €iI ®
...
® V
e
~.im
... ®
€is,
1l ls
L....J
1 r k
m=l
~
(28.42)
-rJ;;k
en
by (2S.35)
where Til"'" k es ek
(T
il
...
i
,).
Equating the components
of
Equations (28.41) and
n-.».
n-;»
(28.42) yields
(28.43)
where only the sum over the subindex
mhas beenexplicitlydisplayed; the (hidden)
sumover
repeated
indicesis, asalways,
understood.

902 28.
DIFFERENTIAL
GEOMETRY
(28.44)
derivation
of
the
relation
between
the
Lie
and
the
covariant
derivatives
Thereis a usefulrelation betweenthe covariautaud the Lie derivativethat we
derivenow.First,letTbeoftype(2, 0) audwriteitinsomeframeasT
=
Tijei®ej.
Applythe covariautderivativewith respect to u to both sides to obtain
VuT=
u(Tij)ei
®
ej
+
Tij
(Vuei) ®
ej
+
Tijei
®
(Vuej).
Similarly,
LuT
=
n(Tij)ei
®
ej
+
Tij
(Luei) ®
ej
+
Tijei
e
(Luej).
Nowuse
Luej
= [u,
ej]
= Vuej - Vejn to get
t.;T = v,T -
Tij
[(Vein) ®
ej
+ei e
(Vejn)].
Ou the other haud,
if
we apply Vu aud L
u
to both sides of
8~
=
(.i,
e
j)
aud
use [u, eil
=
Vuei
-
VeiU'
we obtain
Vue
i
= Lue
i
-
(V
ej
u)'
e
j
.
I!follows that forT =
T;j.i
®
.j,
wehave
.
k'
" k
LuT = VuT+T;j
[(Ve,n)'.
®.J
+(Ve,n)J
.'
®.
].
(28.45)
Onecauuse Equations(28.44) aud (28.45) to generalize to a tensorof type (r, s).
If
n happensto be taugentto a curve t
~
y(t),
Equation (28.40) is written as
DT~·l
...
~r
VuT= JI..·], e. ®
...
® e,'
®.h
®
...
®
.j,
(28.46)
dt
I]
r •
where
DT~I".i!
fdt
'"
Til".i, uk.
In
a coordinateframe, with u
i
= xi =
dx
i
fdt,
EquationsJ
C
i'
lt40) aud
(qlf.fjj
give
DT~l
...
~r
1l •..Js
dt
. .
dxk
dT~l
...i! r
..
. . .
dxk
=
T~I
'r _ =
}I···js
+
~
T~1
...
I.III-1~lm.+l
...
lr
.
rim
,_
lI
]s;kdt
dt
L...J
Jl···JIII-I1mJm+l···J.~
nk
dt
m=l
, "
..
.
dx
k
-
~
TII
.••
lm-llmlm+]
•..
lrrn
_ (2847)
L...J
j!··.jm-In}m+I···}s im
k
dt .
m=l
(28.48)
For the case of a vector (28.47) becomes
Dv
k
dv
k
. k
dx'
--=-+vJr
n-r-r-',
dt
dt
J'
dt
This is au importantequation,to whichwe shallreturn shortly.
Withthegeneralizedgradientoperatordefined,wecaucoustructthedivergeuce
of a tensorjust as in vector aualysis.Given a vector, the divergeuceoperator V·
acts on it aud givesa scalar, or, in the lauguage of tensor aualysis, it lowers the
upperindicesby
1.Thistakesplacebydifferentiatingcomponentsaudcontracting
theupperindexwiththenewlyintroducedindexof differentiation. Thedivergence
of au arbitrarytensoris definedin precisely the same way:
