Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


24.8
REPRESENTATIONS
OF
THE
SYMMETRIC
GROUP
713
standard
Young
24.8.4.Definition. A standardYoung tableau (or diagram,
or
graph) is a Young
tableaux
defined
frame filled with numbers 1 through n such
that
1. the numbers are
placed
consecutively left to right on the rows starting with
1in thefar-left box
of
the first row;
2.· no box
of
any row is to be filled unless all boxes to its left are already filled;
3. at each stage, the number
of
boxes filled in
any
row is never less than the
number
of
rows below it.
regular
graphs
Tableaux satisfying the last condition are called
regular
graphs.
It
followsthatina
Young
tableau,thenumber1is alwaysin theupperleft-hand
box, and that goingdownin a column,the numbersmustincrease.
24.8.5.Theorem.
Let
(A)
be apartition
ofn.
Then the dimension
of
the irreducible
representation T().) is equalto the number
of
standardYoung tableauxassociated
with
(A).
24.8.6. Example. Wewish to calculate the dimensionof each irreduciblerepresentation
of S4.Thepartitionsare (4), (3, I), (2, 2), (2, I, I), and
(1,1,
I, 1)whoseassociatedYoung
framesare shown
below:
ODDO
(4)
DDD
o
(3,1)
DD
DD
(2,2)
DD
D
D
(2,1,1)
o
o
o
o
(1,1,1,1)
The number of standard Youngtableaux associated with
(A)
= (4) is I, because there is
only one way to place the numbers 1 through 4 in the four boxes. Thus, the dimension of
T(4)
is 1. For
(A)
= (3, I), we can place 2 either to the right of I or below it. The first
choicegivesrisetotwo possibilitiesfor the placementof 3:Either to theright of 2orbelow
1.The secondchoice givesrise to only onepossibility for 3, namely to the rightof 1.
With
1,2,
and 3 in place, the position of 4 is predetermined. Thus, we have 3 possibilities for
(A)
= (3, i), and the dimension of
T(3,1)
is 3. For
(A)
= (2,2), we can place 2 either to
the right of I or below it. Both choices give rise tu ouly one possibility for 3:
In the first
case, 3 can ouly
gonoder I; in the second case to its right. With I, 2, and 3 in place, the
position of 4 is again predetermined. Thus, we have 2 possibilities for
(A)
= (2,2), and
the dimensionof
T(3,
1) is 2.The reader maycheck that the dimension
of
T(2,
I,1) is 3, and
that of T(I, I,I,I) is 1.Figure
24.1
summarizesthese findings.Wenotethat the dimensions
satisfy
1
2
+3
2
+2
2
+3
2
+1
2
= 24,the second equation of
(24.18).
l1li

714
24.
GROUP
REPRESENTATION
THEORY
(4)
(3,1)
(2,2)
(2,1,1)
(1,1,1,1)
[IJmwl}]
[TI[1][]
[IJ[]I}]
I}]
rn
[TIm
[IJ[]
[]rn
rnrn
[TIm
[TIl}]
[]
[1]
[±]
DJ
n(3,1) = 3
n(2,1,1)= 3
n(l,I,I,I)
= I
Figure24.1 The
standard
Young
tableaux,
andthe
dimensions
of
irreducible
represen-
tationsof 84.
24.8.3 Graphical Construction of Characters
The product of the symmetric polyuomial S(I) and the antisymmetric polynomial
D(xj)
contains all the information regarding the representations of
S«.
We can
extract the simple characters by looking at the coefficients
of
appropriateproducts
of the x-factors. This can also be done graphically. Without going into the combi-
natorics
of
the derivation of the results, we state the rules for calculatingthe simple
characters, and exantioe one particular case in detail to elucidate the procedure,
whose statement can be very confusing.
As before, we label the irreducible representations with the partitions of
n.
However, we separate out the common factors in a cyclic structure, labeling the
cycles by
li,
12,
etc.
For
example, (2, 1
2
)
has li = 2,
12
= I, and
13
= I. So, we
write
(I)
as (li,
12,
...
,1
m
).
regular
application
24.8.7.
Definition. A regular
opplkation
of
r identical symbols to a Youngframe
is the placement
of
those symbols in the boxes
of
the frame as follows.
Add
the
symbols to any given row,startingwith the thefirst (farthest to the left) unoccupied
cell, until the symbols are all used
6
or the number exceeds that
of
the preceding
6
n
is
understood
that
if
you
cannot
placeall
symbols
onthe
first
row,
thenyou
should
start
atthesecond
row.

positive
and
negative
applications
24.8
REPRESENTATIONS
OF
THE
SYMMETRIC
GROUP
715
line by one. In the latter case, go to the preceding line
and
repeat the procedure,
making sure that the final result
of
adding all r symbols will be a regular graph.
If
in this process the r symbols are divided among an even number
of
rows, we
speak
of
negative application.
If
the number
of
rows is odd, we have a positive
application.
As an illustration, considerthe regularapplication
of
five
2's
to the blankYoung
frame shown below.
0000
000
o
o
We cannot start on the first row because
it
does not bave enongh boxes for the
five
2's.
We can start on the second row and
put
one
2 in the first box. This brings
the number
of
2's
in the second row to
one
more than in the first row; therefore,
we should now go to the first row and
put
the rest
of
the symbols there. We could
start at the
third row,
put
one
2 in the first
box,
put
a second 2 in the first
box
of
the second row, and the rest in the first row. Altogether we will have 3 regular
applications
of
the five 2's. These are shown in
the
diagram below.
rnrnrno
moo
m
o
rnrnoo
moo
rn
rn
Oetailed
analysis
of
the
construction
of
the
character
teble
for5,
Of
these the first and the last tableaux are negative applications, and the middle
oneis
positive.
24.8.8.
Theorem.
Thecharacter
of
the irreducible representation
T(A)
of
the class
(I) = (lJ,12,
...
,1
m)
is obtainedby successive regular applications
oflJ
identical
symbols (usually taken to be 1's), then
lo,
identical symbols
of
a different kind
(usually taken to be 2's), etc. The character
x(W
is then equal to the number
of
ways
of
building positive applications minus the number
of
ways
of
building
negative applications.
The
order in which the Ij's are applied is irrelevant. However, it is usually
convenient to start with the largest cycle.
The
bestway to understandthe procedure is to construct a charactertable.
Let
us do this for 54.As usual, the rows arelabeled
by
the variouspartitions (A)
of4.
We
choose the order (4), (3,
I),
(2,2)
=(2
2
),
(2, 1,
I)
=(2, 1
2
),
(1, I,
I,
1) =(1
4
).
The
columns are labeled by classes (I) in the following order: (1
4
) ,
(2, 1
2
) ,
(2
2
) ,
(3,
I),
(4), where, for example,
(2,1
2
)
means that
11
=2,12 = I, and 13 =
I.
Example 24.8.6 gives us the first column
of
the character table. Similarly, the first
row has 1 in all places, because it is the trivialrepresentation.
Our
taskis therefore

716 24.
GROUP
REPRESENTATION
THEORY
to fill in the rest
of
the table one row at a time. The second row, with (A)= (3, 1),
has a Young frame that looks
like
DOD
o
and for each class (column) labeled (11,
...
,1
m
),
we need to fill this in with 11
identical symbols (1's),
12
identical symbols
of
a different kind (2's), etc.
The second column has 11 =2, lz = 1 =13. So we have two l.'s, one 2, and
one 3.
Ifwe
start with the first row, the two
I's
can be placed in its first two boxes.
If we start with the second row, the two l 's must be placed vertically on top of
each other.
In
the first case, we have two choices for the 2: Either on the first row
next to the two 1's, or on the second line. In the second case, we have only one
choice for the 2: in the first row next to
1.With 1's and 2 in place, the position of
3 is determined. The three possibilities are shown below:
The first two are positiveapplications, the third is negative because the 1's occupy
an even number of rows. We therefore have
(3,1) _ 1 1 1 - 1
X(2,12) - + + - - + .
The third colunm has
1J
=2 =
12.
So we have two 1's and two 2's. We place
the 1's as before. When the two 1's are placed vertically, we can put the
2's
on
the first row and we are done. When the 1's are
initially placed in the first row,
we have no way of placing the
2's
by regnlar application. We cannot start on the
first row because there is only one spot available (remember, we cannot go down
once we start at a row). We cannot start on the second row because once we place
the first 2, we are blocked, and the number of symbols in the second row does not
exceed that of the first row by one. So, there is only one possibility:
Not allowed
Allowed
The only allowed diagram is obtained by a negative application of 1
'So Therefore,
(3,1)
X(2
2)
=-1.
The fourth colunm has
1J
= 3 and h = 1. So we have three 1's and one 2.
There are two ways to place the 1's: all on the first row, or starting on the second
row and working our way up until all boxes are filled except the last box
of
the
first row. The placement
of
2 will be then predetermined.
The
result is the two
diagrams shown below:

24.8
REPRESENTATIONS
OF
THE
SYMMETRIC
GROUP
717
rnrnrn
rn
rnrnrn
rn
The first diagram is obtained by a positive application
of
I's,
the second by a
negative application. Therefore,
(3.1)
X(3.1)
=
+1
-I
=
O.
Finally, for the last column, It = 4. There is only one way to put all the
I's
in
the frame, and that is a negative application. Thus,
X~i1)
=
-l.
Ratherthan going tbruugh the rest
of
the table in die same gory detail, we shall
point ont some of the trickier calcnlations, and leave the rest
of
the table for the
reader to
fill
in. One confusion may arise in the calcnlation
of
xg:;.
The frame
looks like this,
00
DO
and we need to fill this with two
I's
and two 2's. The
I's
can go into the first row
or the first column. The
2's
then can be placed in the second row or the second
column. The resnlt is
The first diagram has no negative application. The second has two negative ap-
plications, one for the
I'
s, and one for the 2' s. Therefore, the overall sign for the
second diagram is positive.
It
follows that
xg:;
=+ I + I =
+2.
The calcnlation of
x~)')
may also be confusing. We need to place four
I's
in
the frame.
If
we star! on the first row, we are stuck, because there is roomfor only
two
I's.
If
we star! in the second row, then we can only go up: Putting the first
I in the second row causes that row to have one extra I in comparison with the
precedingrow.However, once we go up, we have room for only two
I's
(we cannot
go back down). So, there is no way we can place the four
I's
in the (2
2
)
frame,
(2')
and X(4) =
O.
The character table for 84 is shown in Table 24.6 (see Problem24.15 as well).
The reader is urged to verify all entries not calcnlated above. The character table
for 85 can also be calcnlated with only minor tedium. We quote the resnlt here in
Table 24.7 and let the reader check the entries
of
the table.
24.8.4
Young
Operators
The group algebratechniques of Section
24.4-which
we used in our discussionof
representation theory in a very limited
way-provide
a powerful and elegant tool

718 24.
GROUP
REPRESENTATION
THEORY
(1
4
)
(2,1
2
)
(2
2
)
(3,
I)
(4)
T(4)
I
I I I I
T(3.1)
3
I
-I
0
-I
T(2')
2 0 2
-I
0
T(2,!')
3
-I
-I
0 I
T(l4)
I
-I
I I
-I
Table24.6 Cbaractertablefor 54.Therowsandcolumns arelabeledby the partitionsof
4 andcycle
structures,
respectively.
for unraveling the representations
of
finite gronps. These techniqnes have
been
particnlarly useful in the analysis
of
the representations
of
the synnnetric group.
Our
emphasis on the synnnetric group is
not
merelydue to the importance
of
S«
as
a paradigm
of
all finite groups.
It
has also to do with the unexpected usefulness
of
the representations
of
S«
in stndying the representations
of
GL(V),
the paradigm
of
all (classical) continuous groups. We shall
come
back
to this observation later
when we discuss representations
of
Lie
groups in Chapter27.
To begin with, consider the element
of
the Sn group algebra as defined in
Equation
(24.22). Since mnltiplying P (on the left) by a group element does
not
change P, the ideal generated by P is
not
only one-dimensional,
but
all elements
of
Sn are represented by the number I. Therefore, the ideal
AP
corresponds to the
(irreducible) identity representation.
For
Sn, there is another group algebra element
that
has similarproperties. This
is
n!
Q=
LE
n i
11"
j ,
i=l
(24.62)
The reader may check that
and
Q2
=n!Q.
As in the
case
of
P, Q generates a one-dimensional ideal, but a left mnltiplication
may introduce a minus sign (when the permutationis odd). Thus, the ideal gener-
ated by
Q
must
correspond to the antisynnnetric (or alternating) representation.
All the irreducible representations, including the special one-dimensional
cases above, can be obtained using this group-algebraic method. We shall
not
give the proofs here, and we refer the reader to the classic
book
[Boer 63,
pp.
102-125]. The starting
point
is the Young frame corresponding to the par-
tition
(A) = (AI,
...
, Am). One puts the numbers I through n in the frame in any
order, consistent with tableau construction, so that the
end
product is a Young
tableau.
Let
p be any permutation
of
a Young tableau that does
not
changethe row

horlzonlal
and
vertical
permutations
Young
operators
defined
24.8
REPRESENTATIONS
OF
THE
SYMMETRIC
GROUP
719
(15)
(2, 1
3
)
(2
2
,
I)
(3,2) (3, 1
2
)
(4,
I)
(5)
T(5)
I I
I
I
I
I I
TC4.1)
4
2 0
-I
I
0
-I
TC3.2)
5 I
I
I
-I
-I
0
TC3.1')
6 0
-2
0
0 0
I
T(2'.1)
5
-I
I
-I
-I
I 0
T(2.1')
4
-2
0
I
I
0
-I
T(l')
I
-I
I
-I
I
-I
I
Table 24.7 Character tablefor S5. Therowsandcolumnsarelabeledbythepartitionsof
5 andcycle
structures,
respectively.
of
the numbers it acts on. Such a p is called a
horizontal
permutation.
Similarly,
let
q be a vertical
permutation
of
the Young tableau, i.e., a permutation that does
not change the column of the nnmbers it acts on.
24.8.9. Definition.
Considerthe
kth
Young tableau corresponding to the partition
(A).
Let
the Young symmetrizer PF')
and
antisymmetrizer
Qk
A
)
be the elements
of
the group algebra
of
Sn defined as
CA)
""'
P
k
=
L..P'
p
Then, the Young operator Y1
A
)
of
this tableau, anotherelement
of
the group alge-
bra, is given by Y1
A
) =
Qf)
PF').
It
can be shown that the following holds.
24.8.10.
Theorem.
The Young operator YF') is essentially idempotent,
and
gen-
erates a minimal left ideal, hence an irreducible representation
for
Sn. Represen-
tations thus obtainedfrom different frames are inequivalent. Different tableaux
with the same frame give equivalentirreducible representations.
In practice, one usually chooses the standard Yonng tableaux and applies the
foregoing procedure to them to obtain the entire collection of inequivalent
irre-
ducible representations of Sn. We have already seen how to calculate characters
of
Sn employing both analytical and graphical methods. Theorem 24.8.10 gives
yet another approach to analyzing representations
of
Sn.
For
low values of n this
technique may actually be used to determine the characters, but as
n grows, it
becomes unwieldy, and the graphical method becomes more manageable.

720
24.
GROUP
REPRESENTATION
THEORY
24.8.11.Example. Let us apply this method to S3.
The
partitions are (3), (2,
I),
and
(1
3).
There is only
one
standard Young tableau associated with (3) and (1
3).
Thus,
wherewehave
divided
these
Young
operators
by 6to makethem
idempotent;
wehavealso
used the notatioo
of
Example 23.4.1.
One
can
show directly that y(3)
y(l')
=
O.
In fact,
one
can prove this for general
Sn
(see Problem 24.30).
Forthe
partition
(2, 1),
there
aretwo
Young
tableaux.
The
first
onehasthe
numbers
1
and
2 in the
first
row
and
3 inthe
second.
In thesecond
tableau
the
numbers
2
and
3 are
switched.
Therefore,
usingthe
multiplication
table
for 83 as givenin
Example
23.4.1,we
have
y?,I)
= Q\2,1)
p?,l)
= (e -
"3)(e
+
"2)
= e +
"2
-
"3
-
"6,
y?,I)
=
Q~2,1)
p?,I)
= (e
-'''2)(e
+
"3)
= e -
"2
+
"3
-
"5.
The
reader
mayverify
that
the
product
of anytwo
Young
operators
corresponding
to
different
Young
tableaux
is zeroand
that
Y
(2,I)y (2,1) _ 3y(2,1)
1 1 - 1 •
Letus
calculate
theleft ideal
generated
by these
four
Young
operators.
We
already
know from
our
discussion at the beginning
of
this subsection that£,(3) and £,
(I'),
the ideals
generatedby
y(3) and
y(l')
,are one-dimensional.
Let
us find £,\2,I), the ideal generatedby
y?'
I)
This is the span
of
all vectors obtained
by
multiplying
y?'
I) on the leftby elemeuts
of
the group algebra. It is sufficient to multiply
y?'
I) by the basis
of
the algebra, uamely
the
group
elements:
Y
(2,1) _ y(2,1)
e 1 - 1 '
"2
Y
?'I) =
"2
+e -
"5
-
"4
ea X\2,I) ,
"3
y
? ,I) = "3
+"6
- e - "2 =
-y?,I),
"
4YI(2,
I) =
"4
+
"5
-
"6
-
"3
= -
X\2,
I) +
y?,
I),
"5
y?,1)
=
"5
+
"4
-
"2
- e = _X\2,1),
"6
y?,I)
=
"6
+
"3
-
"4
-
"5
= X\2,1) _
y?,I)
It
follows from
the
above calculation that
£,~2,
I). as a vector space, is spanned by
{Y?'
I),
x?'
I)}, andsincethesetwo
vectors
are
linearly
independent,
Li
2
,1)is a
two-dimensional
minimal
ideal
corresponding
to a two-dimensional
irreducible
representation
of 83. One
canusethisbasis
to
find
representation
matrices
andthesimple
characters
of 83.

24.8
REPRESENTATIONS
OF
THE
SYMMETRIC
GROUP
721
Theothertwo-dimensionalirreduciblerepresentationofS3,equivalentto theone
above,
is obtained by constructing the
ideal.ci
2
,1) generated by
yi
2
,1). This construction is left
forthe
reader,
whois alsoaskedto verifyits dimensionality.
The resolution
of
the identity is easily verified:
The
ej's
are idempotents that satisfy
ejej
= 0 for i
:F
j.
24.8.5 Products of Representations of
S«
In
the quantumtheoryof systemsof many identicalparticles,the wavefunction
musthaveaparticularsymmetryunderexchangeoftheparticles:
If
theparticlesare
allfermions(bosons), theoverallwavefunctionmustbecompletelyantisymmetric
(symmetric). Sincethespaceoffunctionsof severalvariablescanprovideacarrier
spacefor the representation of anygroup, we can, in the case of
Sn, thinkof the
antisymmetric (symmetric) functions as basis functions for the one-dimensional
irreducibleidentity(alternating)representation. Toobtainthesebasisfunctions, we
applythe
Young
operator
y(l")
(or yIn») tothe argrunents of anygivenfunctionof
n variablestoobtainthecompletelyantisymmetric(orsymmetric)wavefunction."
Undercertainconditions, we may require mixed symmetries. For instance,in
thepresenceofspin,theproductofthetotalspinwavefunctionandthetotal space
wavefunction must be completelyantisymmetric for Fermions.Thus, the space
part(orthespinpart)ofthewavefunctionswill,ingeneral,havemixed
symmetry.
Sucha mixedsymmetrycorresponds to someother
Young
operator,and the wave
functionis obtainedby applyingthat
Young
operatorto the argnments of thewave
function.
Nowsupposethatwehavetwo separatesystemsconsistingof
nl
and
n2
parti-
cles,respectively, whichareallassumedtobeidentical.Aslongasthetwosystems
are not interacting, each will consist of states that are classifiedaccordingto the
irreduciblerepresentations ofits symmetricgroup.Whenthetwosystemsinteract,
we shouldclassifythestatesof thetotal systemaccordingto theirreduciblerepre-
sentations of all
nI +nz particles.Wehavealreadyencounteredthe mathematical
procedurefor such classification:
It
is the Clebsch-Gordan decompositionof the
directproductofthestatesofthetwosystems.Sincetheinitialstatescorrespondto
Young
tableaux, and sincewe are interestedin the inequivalentirreduciblerepre-
sentations, we needto examinethe decompositionof the directproductof
Young
frames into a sum of
Young
frames. Wefirst state (withoutproof) the procedure
for sucha decomposition, and then givean exampleto illustrate
it.
24.8.12.Theorem.
To
find
thecomponents
of
Young
frames in theproduct
of
two
Young
frames, drawone
of
theframes. In theother
frame,
assignthesamesymbol,
7We must make the additional assumption that the permuted functions are all independent.
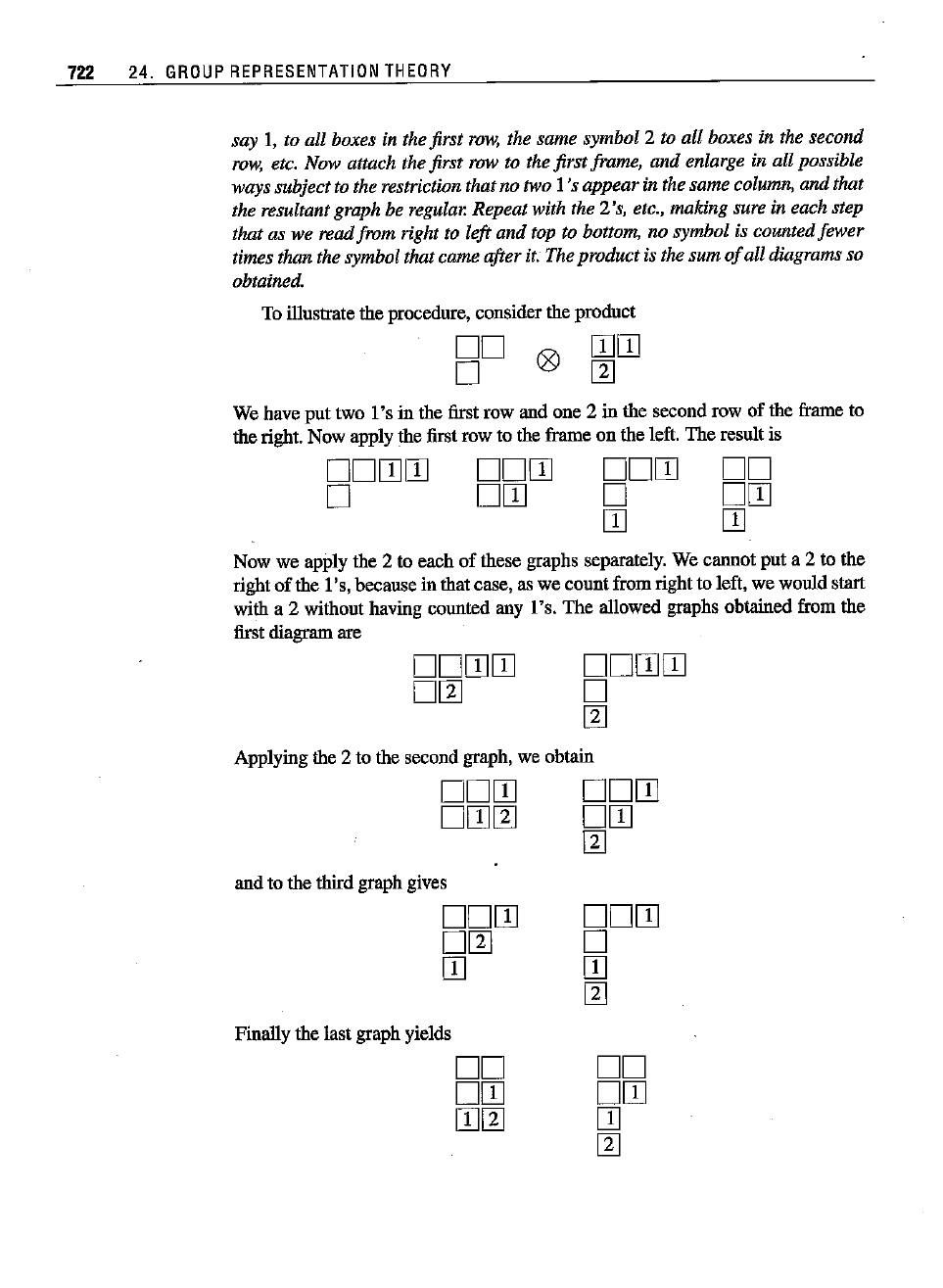
722
24.
GROUP
REPRESENTATION
THEORY
say I, to all boxes in the first row, the same symbol 2 to all boxes in the second
row, etc. Now attach the first row to the first frame,
and
enlarge in all possible
ways subjectto the restriction that no two
I 's appear in the same column, and that
the resultant graph be
regular.
Repeatwith the 2's, etc., making sure in each step
that as we read from right to left
and
top to bottom, no symbol is countedfewer
times than the symbol that came after it. The productis the sum
of
all diagrams so
obtained.
To illustrate the procedure, cousider the product
00
o
We have put two
I's
in the first row and one 2 in the second row of the frame to
the right. Now apply the first row to the frame on the left. The result is
oOITJm
o
oom
om
oom
o
rr
00
om
ITJ
Now we apply the 2 to each of these graphs separately. We cannot put a 2 to the
right
of
the I's, because in that case, as we count from right to left, we would start
with a 2 without having counted any
I's.
The
allowed graphs obtained from the
first diagram ate
oomm
om
oomm
o
m
Applying the 2 to the second graph, we obtain
oom
oITJm
and to the third graph gives
oom
om
m
Finally the last graph yields
OOITJ
om
m
oom
o
m
rn
00 00
om
om
mrn
OJ
m
