Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.

21.5
PERTURBATION
THEORY
603
(a)
(b)
~
y
Yz
X
YI
(c)
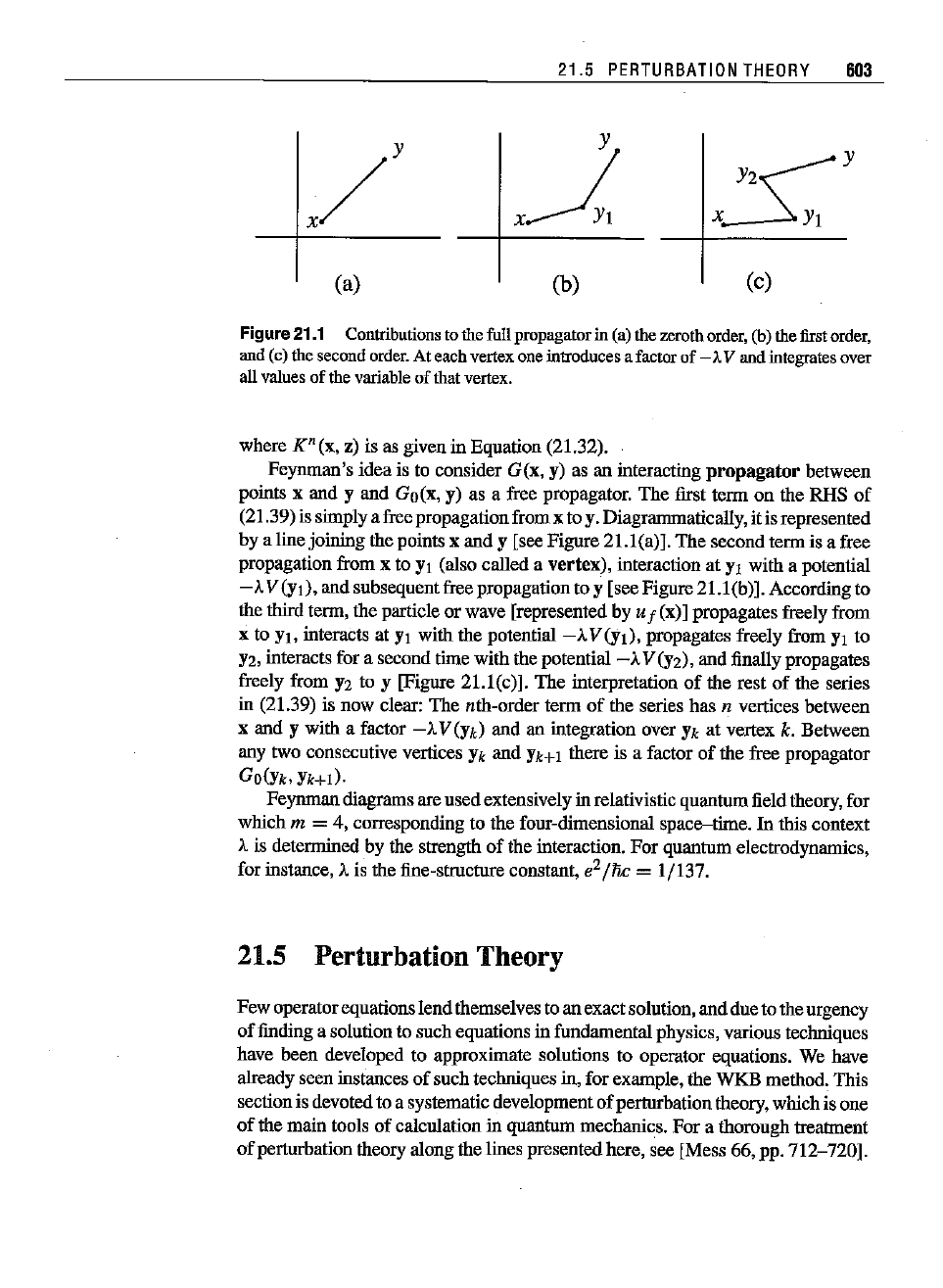
Figure21.1 Contributions tothefullpropagatorin (a)thezerothorder,(b) thefirstorder,
and
(c)the
second
order.
Ateach
vertex
one
introduces
a
factor
of -}..V and
integrates
over
all
values
ofthe
variable
of
that
vertex.
where K" (x, z) is as given in Equation (ZI.32).
Feynman's
idea
is to consider G(x, y) as an interacting propagator between
points x and y
and
Go(x, y) as a free propagator.
The
first term on the RHS
of
(21.39) is simplya free propagationfrom x to y. Diagrammatically,it is represented
by
a linejoiningthe points x and y [see
Figure
21.1(a)].
The
second termis a free
propagation from x to YI (also called a
vertex),
interaction at YI with a potential
-A
V(yI), and subsequentfree propagation to y [see Figure21.1(b)]. According to
the third term, the particle or wave [represented by U f (x)] propagates freely from
x to YI, interacts at YI with the
potential-AV(YI),
propagates freely from YI to
Y2,
interacts for a second time
with
the potential
-A
V(Y2), and finally propagates
freely from
Y2
to y [Figure 21.1(c)].
The
interpretation
of
the rest
of
the series
in (21.39) is now clear:
The
nth-order term
of
the series has n vertices between
x and Ywith a factor
-AV(Yk)
and
an integration over Yk at vertex k. Between
any two consecutive vertices
Yk
and
Yk+I there is a factor
of
the free propagator
GO(Yk,
Yk+l).
Feynmandiagrams are usedextensively in relativistic quantumfield theory, for
which
m = 4, corresponding to the four-dimensional space-time.
In
this context
Ais determined by the strength
of
the interaction.
For
quantum electrodynamics,
for instance, Ais the fine-structure constant,
e
2
/
1i.c
=
1/137.
21.5 Perturbation Theory
Few
operatorequations
lend
themselves to an exactsolution,
and
due
to the urgency
of
findiug a solution to suchequations in fundamental physics, various techniques
have been developed to approximate solutions to operator equations. We have
already seen instances
of
suchtechniques
in,
for example,the
WKB
method.This
sectionis devotedto a systematic development
of
perturbationtheory, whichis one
of
the main tools
of
calculation in quantum mechartics.
For
a thorough treatment
of
perturbation theory along the lines presentedhere, see [Mess 66, pp.
712-720].

604 21. MULTIDIMENSIONAL
GREEN'S
FUNCTIONS:
FORMALISM
The
starting point is the resolvent (Definition 16.8.1)
of
a Hamiltonian H,
which, using z instead
of
A, we write as Rz(H).
For
simplicity, we assume that
the eigenvalues
of
H are discrete. This is a valid assumption
if
the Hamiltonian
is
compact
orif we are
interested
in
approximations
close to one of the
discrete
eigenvalues. Denoting the eigenvalues
of
H by
{Ed;::;o,
we have
(21.40)
where
Piis the projectionoperatorto the ith eigenspace. We
can
write the resolvent
in terms
of
the projection operators by using Equation (16.8):
00
Pi
Rz(H) =
L--'
i=O Ei - Z
(21.41)
The
projection operator Pi
can
be written as a contour integral as in Equation
(16.13). Any sum
of
these operators can also be written as a contour integral. For
instance, if
r is a circle enclosing the first n +1 eigenvalues, then
n 1 i
Pr
==
LPi
=
--.
Rz(H)dz.
i=O
2.7rl
J'
(21.42)
Multiplying Equation (21.42) by
H and using the definition
of
the resolvent,
one
can show that
HPr = - 2
1
. J zRz(H) dz:
m ir
(21.43)
When
r includes all eigenvalues
of
H,
Pr
= 1, and Equation (21.43) reduces to
(16.12) with A
--+
T and
f(x)
--+
x.
To proceed, let us assume that H = Ho +
AV
where Ho is a Hamiltonian with
perturbing
potential
knowneigenvalues and eigenvectors, and Vis aperturbingpotential; Ais a (small)
parameter that keeps track
of
the order.
of
approximation.
Let
us also use the
abbreviations
G(z) es
-Rz(H)
and
Go(z) sa
-Rz(Ho).
(21.44)
Then a procedure very similarto that leading to Equation (21.37) yields
G(z) = Go(z) +AGo(z)VG(z),
which
can
be expanded in a Neumano series by iteration:
00
G(z) =
LAnGO(zHVGo(z)]".
n=oO
(21.45)
(21.46)
Let
{E~l,
{M~
I,and
rna
denote,respectively, the eigenvalnes
of
Ho,theircorre-
sponding eigenspaces, and the latter's dimensions.e
In
the context
of
pertorbation

Degeneracy
is
the
dimension
of
the
eigenspace
of
the
Hamiltonian.
21.5
PERTURBATION
THEORY
605
theory,
rna
is called the degeneracy
of
E2,
and
E2
is called rna-fold degener-
ate,
with a similar terminology for the perturbed Hamiltonian. We assnme that all
eigenspaces have
finite
dimensions.
Itis clear that eigenvalnes
and
eigenspaces
of
Hwill tend to those
of
Ho
when
A
--> O.So, let us collectall eigenspaces
of
Hthat tend to
M2
and
denote them by
{Jv(f};~1'
Similarly, we use
Ei
andPfto denote,respectively,the energyeigenvalue
and the projector to the eigenspace
Mi.
Since dimension is a discrete quantity, it
cannot depend on A,and we have
'"
Ldim
Mi
=
dimM~
= rna.
i=l
(21.47)
We also use the notation P for the projector onto the direct snm
of
Mi's.
We thus
have
and
HmP=P~,
).-->0
(21.48)
where we have used an obvious notation for the projection operator onto
M2.
The
main task
of
perturbation theory is to find the eigenvalues and eigen-
vectors
of
the perturbed Hamiltonian io terms
of
a series io powers
of
A
of
the
corresponding unperturbed quantities. Sioce the eigenvectors-c-or,
more
appro-
priately, the projectors onto
eigenspaces-and
their corresponding eigenvalues
of
the perturbed Hamiltonian are related via Equation (21.40), this task reduces to
writing P as a series in powers
of
Awhose coefficients are operators expressible
io terms
of
unperturbed quantities.
For sufficiently small A,there exists a contourio the z-plane enclosiog
E2
and
all E't's but excludiog all other eigenvalues
of
H
and
Ho.Denote this contour by
ra and, nsiog Equation (21.42), write
P =
~
J
G(z)dz.
2nl
ira
Itfollows from Equation (21.46) that
00
p=p2+
I>nA(n),
Il=l
where
A(n)
==
_1_. J Go(z)[VGo(z)]" dz:
21r1
Yr"
(21.49)
This equation shows that perturbation expansion is reduced to the calculation
of
A(n), which is simply the residue
of
Go(z)[VGo(z)]n.
The
only siogularity
of
the
iotegrand in Equation (21.49) comes from
Go(z), which, by (21.44)
and
(21.41),
2Weusethebeginning
letters
of theLatin
alphabet
forthe
unperturbed
Hamiltonian.
Furthermore, we
attach
a
superscript
"0"
to emphasizethattheobjectbelongs to
HO'

606 21. MULTIDIMENSIONAL
GREEN'S
FUNCTIONS:
FORMALISM
has a pole at E2. So, to calculate this residue, we simplyexpaodGo(z)in a Laurent
series about
Eg:
pO pO pO
Go(z) = L
~
=
_a_
o
+L
~
b Z - E
b
Z -
E
a
b'!a
Z - E
b
° pO
Pa
~
b
=
---0
+
L."
°
z- E
a
b'!a
(Eo _
EO)
(I
+ z - E
a
)
a b
E2-
E
g
pO
00
(z _
EO)kpO
__
a_
~~(_I)k
a b
- Z -
EO
+
L."
L."
(EO
_ EO)k+1 .
a b¥=ak=O a b
Switching the orderof the two sums, aod noting that our space is the Hilbert space
of
Howhose basis cao be chosen to consist of eigenstates
of
Ho,we cao write Ho
instead
of
Eg
in the denominator to obtain
where we have used the completeness relation for the Pg's, the fact that
Q2
com-
mutes with
Ho [aod, therefore, with
G~+l
(E2)], aod, in the last equality, the fact
that
Q2
is a projection operator.'
It
follows that
pO
00
Go(z) = 7 +
L(-Ihz
-
E2)kQ2G~+1(E~)Q~
Z - a k=O
00
=
L(-lhz
-
E~)k-lSk,
k=O
where we have introduced the notation
(21.50)
if
k = 0,
if
k:o>:1.
3Note
that
although
Go
(z) hasa poleat
E~.
the
expressions
in thelastline of the
equation
abovemakesense
because
Q~
annihilates
allstateswitheigenvalue
E~.
Thereasonforthe
introduction
of
Q~
onbothsidesis toensure
that
G~+
1
(E~)
will not
actonan
eigenstate
of
E~
on
either
side.

21.5
PERTURBATION
THEORY
607
By substituting Equation (21.50) in Go(z)[VGo(z)]n we obtain a Laurent ex-
pansion whose coefficient of (z - E2)-1 is
A(n).
The reader may check that such
a procedure yields
A(n)
=
(_1)"+1
LSk1VSk'V
...
VSk"+l,
(n)
(21.51)
where by definition,
L(p)
extends over all nonnegative integers {ki
}?~l
such that
n+l
Lki=p
i=l
vp
::::0.
It
turns out that for perturbatiou expansion,
uot
ouly do we need the expansion of
P [Equations (21.49) and (21.51)], but also an expansion for HP. Using Equations
(21.43) and (21.44), with r replaced by r
a,
we have
HP =
~
J zG(z)dz =
---.!:...,
J (z - E2 +E2)G(z)dz
21ft
ft
a
27fl
jr
a
=
---.!:...,
J (z - E2)G(z) dz +E2p.
2Jrl
ft
a
Substituting for
G(z)
from Equation (21.46), we can rewrite this equation as
00
(H - E2)p =
L}.nB(n),
n=l
where
B(n)
=
(_l)n-l
L Sk'
V
Sk'V·
..
VS
k
"+l
(n-l)
(21.52)
(21.53)
Equations (21.52) and (21.53) can be used to approximate the eigenvectors
and eigenvalues of the perturbed Hantiltonian in terms of those
of
the unperturbed
Hamiltonian. It is convenient to consider two cases: the nondegenerate case in
which
rna
= 1, and the degenerate case in which
rna
::::
2.
21.5.1 The Nondegenerate Case
In
the nondegenerate case, we let
12)
denote the original unperturbed eigenstate,
and use Equation
(21.47) to conclude that the perturbed eigenstate is also one-
dimensional.
Infact, it follows from (21.40) that P
I~)
is the desired eigenstate.
Denoting the latter by
Ilfr)
and using Equation (21.49), we have
00 00
Ilfr)
= P
12)
=
p212)
+
L}.nA(n)
I~)
=
I~)
+
L}.nA(n)
12)
n=l n=l
(21.54)

608 21. MULTIDIMENSIDNAL
GREEN'S
FUNCTIDNS:
FDRMALISM
because
P~
is the projection operator onto
I~).
More
desirable is the energy
of
the perturbedstate E
a
,
whichobeys the relation
HP =
EaP.
Taking the trace
of
this relation
and
noting that
tr
P =
tr
P~
= I, we
obtain
e, = tr(HP) =
tr
(E~P
+
~
A
nB(n»)
(21.55)
(21.57)
first-order
correction
to
energy
second-order
correction
to
energy
where we used Equation (21.52). Since A is sinnply a parameter to keep track
of
the order
of
perturbation,
one
usually includes it in the definition
of
the perturbing
potential
v.The nth-order correctionto the energy is then written as
en
=
tr
B(n)
. (21.56)
Sinceeach
term
of
B(n)
contains
p~
atleast once, andsince
tr(UP~T)
=
tr(TUP~)
for any
pair
of
operators U
and
T (or products thereof). one
can
cast
en
into the
form
of
an expectationvalue
of
some
product
of
operators in the unperturbed state
I~).
For example,
el
=
tr
B(I) =
L:
(g
I
P~VP~
Ig)
=
(~I
V
I~)
b
because
P~
Ig)
=0 unless b =a. Thisis the familiar expression for the first
order
correction
to the energy in nondegenerale perturbation theory. Similarly,
ez=
tr
B(2)
- - tr (poVpoV[-OoGk(Eo)Oo]
-
aa
aQaa
+poV[_OoGk(Eo)Oo]Vp
o
+ [_OoGk(Eo)Oo]VpoVp
o)
a
aOaaa
aOaaaa
=
(~I
VO~G~(E~)O~V
I~).
The
first
andthelasttermsinparentheses give zero becausein the
trace
sum,
p~
gives a nonzero contribution only if the state is
I~),
which is precisely the stale
anniltilated by
O~.
Using the completeness relation
Lb
Ig)
(gl
=1 = L
c
I~)
(~I
for the eigenstates
of
the unperturbed Hamiltonian, we can rewrile ezas
This is the familiar expression for the
second-order
correction
to the energy in
nondegenerate perturbation theory.

21.5
PERTURBATION
THEORY
609
21.5.2 The DegenerateCase
The degenerate case can also start with Equations (21.54) and (21.55). The differ-
ence is that
en
cannot
be determined as conveniently as the
nondegenerate
case.
Forexample,theexpression for81 will involvea sumoverabasis of
Jv(~
because
P~
Ig}
is no longer
just
I~)'
but somegeneral vectorin
JY[~.
Instead
of
pursuing this
line of
approach,
we presentamorecommonmethod,whichconcentrates on the
way
JY[~
and the corresponding eigenspaces of the perturbedHamiltonian, denoted
by
JY[a, enterin the calculation
of
eigenvalues and eigenvectors.
The projector
P~
acts asa unit operator
when
restrictedto
JY[~.
In particular, it is
invertible. In the limit
of
small A,the projectionoperatorPis closeto
P~;
therefore,
it too must be invertible, i.e.,
P :
JY[~
-+
JY[a
is an isomorphism. Similarly,
P~
:
JY[a
-+
JY[~
is also an
isomorphism-not
necessarily the inverse
of
the first one.
It
follows that for each vector in
JY[~
there is a unique vector in
JY[a
and vice versa.
The eigenvalue equation
H lEa) = E
a
lEa)
can
thus be written as
HP
a
IE2} =
EaP.
IE2) ,
where IE2) is the unique vector mapped onto
IE.)
by pa- Multiplying both sides
by
P~,
we obtain
P2HP
a
IE2} =
EaP~Pa
IE2) ,
which is completely equivalent to the previous equation because
P~
is invertible.
If
we define
H
a
==
P~HPaP~
:
M~
->
JV(~,
the preceding equation becomes
H
a
IE2} =
EaK"
IE~}.
(21.58)
(21.59)
As operators on
JY[~
both H
a
and K
a
are hermitian. In fact, K",whichcan be written
as the product of
P~Pa
and its hermitian conjugate, is a positive definite operator.
Equation (21.59) is a generalized eigenvalue equation whose eigenvalues
E
a
are
solutions of the equation
det
(H
a
-
xK,,) = O.
(21.60)
The eigenvectors
of
this equation, once projected onto
JY[a
by P
a,
give the desired
eigenvectors
of
H.
The expansions of H
a
and K
a
are readily obtaiued from those
of
HPa and Pa
as given in Equations (21.49) and (21.52). We give the first few terms of each
expansion:
K" =
~
-
A2~VQ~Gt(E~)Q~V~
+...,
E
o 'po °
,2
°
QOG
(EO)QO
°
H
a
=
aKa+A
.VPa+A
PaVaO
a
aVPa+,.··
(21.61)

610 21. MULTIDIMENSIONAL
GREEN'S
FUNCTIONS:
FORMALISM
Toany given orderof approximation, the eigenvalues E
a
are obtainedby terminat-
ing the series in (21.61) at that order, plugging the resulting finite sum in Equation
(21.60), and solving the determinant equation.
21.6 Problems
21.1. Show that the definitions
of
thethree types
of
SOPDEsdiscussedin Example
21.1.8 are equivalentto the definitionsbasedon Equation (21.5). Hint: Diagonalize
the matrix of coefficients of the SOPDE:
a
2u
a
2u
a
2u
( au
au)
a-
2
+2b-
a
a
+c-
2
+F
x,y,u,
-a
'-a
=0,
ax x y ay x y
where a, b,and c are functions
ofx
and y. Write the eigenvalues as (a
+c±
1:;.)/2
and consider the three cases
II:;.I
<
la
+c],
II:;.I
>
la
+c], and
II:;.I
=
la
+c].
21.2. Find the characteristic curves for
Lx[u] =
au/ax.
21.3. Find the characteristic curves for the two-dimensional wave equation and
the two-dimensional diffusion equation.
21.4. Solvethe Cauchyproblemfor the two-dimensionalLaplaceequationsubject
to the Cauchy data
u(O,y) = 0,
(au/ax)
(0, y) = E
sinky,
where E and k are
constants. Show that the solution does not vary continuously as the Cauchy data
vary.
In
particular,show that for any E
i'
°and any preassignedx > 0, the solution
u(x, y)
can
he made arbitrarily large by choosing k large enongh.
21.5. Show that the
Xi in Equation (21.12) describe an m-dimensional sphere
of
radius
r,
that
is,
Lr=l
xl
=
,2.
21.6. Use
J8(x
- a) = 8(e -
a)
and the coordinate transformation from the
spherical coordinate system to Cartesian coordinates to express the 3D Cartesian
delta function in terms
of
the corresponding spherical delta function at a point
P =(xo,
Yo,
zo) =(ro,
1J0,
9'0) where the Jacobian J is nonvanishing,
21.7. Find the volmne of an m-dimensional sphere.
21.8. Prove Equation (21.11). First, note that the RHS of Equation (21.10) is a
function of only
k of the a's. This means that
(a) Rewrite Equation(21.10) by separatingthe integralinto two parts, one involving
{~;\~~1
and the other involving
(~;\;n~k+l'
Compare the RHS with the LHS and
show that
J
Jd~k+l'"
d~m8(x-a)
=
fI8(~i
-ail·
i=l

21.6
PROBLEMS
611
(b) Show thatthisequation implies that 8(x - a) is independent
of
Rilf'~k+l'
Thus,
one can take the delta function out of the integral.
21.9. Findthe m-dimensional Green's function for the Laplacian as follows.
(a) SolveEquation (21.19) assuming that
r
oF
0 and demanding that
G(r)
-+
0 as
r
-+
00
(this can be done only for m 2: 3).
(b) Use the divergence theorem in m dimensions and (21.18) to show that
II
~~
da=
I,
s
where S is a spherical hypersurface
of
radius r. Now use this and the result of part
(a) to find the remaining constant
of
integration.
21.10. Consider the operator
Lx
= V
2
+b . V +c for which
{hilf'~l
and c are
functions of
{x;
}f'~1'
(a) Show that
!J[v]
= V
2
v - V . (bv) +cv, and
Q[u, v*] =Q[u, v] =
vVu
-
uVv
+
buv.
(b) Show thatanecessaryconditionfor Lxto be self-adjointis Zb-
Vu+u(V
-b) = 0
for arbitrary
u.
(c) By choosing some u'sjudiciously, show that (b) implies that hi =
O.
Conclude
that
Lx
= V
2
+
c(x)
is formally self-adjoint.
21.11. Solve the integralform of the Schrodingerequationfor an attractive double
delta-function potential
Vex) =
-Vo[8(x
-
al)
+8(x - a2)],
Vo >
O.
Find the eigenfunctions and obtain a transcendental equation for the eigenvalues
(see Example 21.4.1).
21.12. Show that the integral equation associated with the damped harmonic os-
cillatorDEx
+2yi
+w5x = 0, having the
BCs
x(O) = xo,
(dx/dt)t~o
= 0, can
be written in either of the following forms.
w21t
(a)
x(t)
=
Xo
-
--..!!
[1-
e-
2y
(t- t')]
x(t')
dt'.
2y °
(h)
x(t)
= xocoswot +
2y
xO
sinwot - 2y
['
cos[wo(t -
t')]x(t')dt'.
wo
io
Hint: Take w5x or
2yi,
respectively, as the inhomogeneous term.
21.13. (a) Show that for scattering problems
(E
> 0) the integral form
of
the
Schrodinger
equation
in onedimension is
ljI(x)
= e;kx _
i~
1
00
e;klx-yl
V(y)ljI(y)
dy.
fj k
-00

if [x] < a,
if
Ixl
> a,
612
21. MULTIDIMENSIONAL
GREEN'S
FUNCTIONS:
FORMALISM
(b) Divide
(-00,
+00)
into three regions
Rl
=
(-00,
-a),
Rz =
(-a,
+a),
and
R3 = (a, 00). Let l!ri(X) be
'f!(x)
in region Ri, Assume that the potential
V(x)
vanishes in R1 and R3. Show that
'f!1(X) = e
'kx
_
i':
e-
ikx
1
a
e'kYV(y)'f!z(y)dy,
Ii k
-a
'f!z(x) = e
'kx
-
~~
i:
e'klx-yIV(y)'f!z(y)dy,
'f!3(X) = e
ikx
_
.!..!!:.-e
lkx
1
a
e-lkYV(y)'f!z(y)dy.
Itzk
-a
This shows thatdeterminingthe wave functioninregionswherethereis no potential
requires the wave function in the region where the potential acts.
(c) Let
V(x)
=
{~o
and find 'f!z(x) by the method
of
successive approximations. Show that the
nth
term is less than
(21-'
Voa/ItZk)n-l
(so the Neumann series will converge)
if
(2Voa/ ltv) < I, where v is the velocity and I-'v = Iik is the momentum
of
the
wave. Therefore, for large velocities, the Neumann series expansion is valid.
21.14. (a) Show that HRz(H) = 1
+zRz(H).
(b) Use (a) to proveEquation (21.43).
Additional Reading
1. Folland, G.Introduction to PartialDifferentialEquations, 2nded.,Princeton
University Press, 1995. Discusses multidimensional Green's functions for
various differential operators
of
mathematical physics.
2. Messiah,
A. QuantumMechanics, volume
II,
Wiley, 1966. A thoroughtreat-
ment
of
perturbation theory in the style
of
this chapter.
3. Stakgold.L
Green'sFunctions
and
Boundary
Value Problems, Wiley, 1979.
A detailedanalysis
of
boundaryvalue problemsin two and threedimensions.
