Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


20.3
GREEN'S
FUNCTIONS
FOR
SOlDOS
573
In particular, if
Lx[u]
= 0, theu
u(y)
=0 for all y. We have proved the following
result.
20.3.7.
Proposition.
The
DE
Lx[u]
= 0
implies
that
u sa 0 if
and
only
ifthe
GF
corresponding to
lx
and
the homogeneous
Bes
exist.
lt
is sometimes stated that the Green's function
of
a SOLDO with constant
coefficients depends on the difference
x - y. This statement is motivated by the
observation that
if
u
(x)
is a solution
of
d
2u
du
Lx[u]
=a2
dx
2
+
al
dx
+aou =f
ix),
then
u(x
-
y)
is the solution
of
a2u"
+
alu'
+aou =
I(x
-
y)
if
ao,
ai,
and a2
are constant. Thus,
if
G(x)
is a solution
of
Lx[G] =
8(x)
[again assuming that
w(x)
=I], thenit seemsthatthe solution
of
Lx[G] =
8(x
-
y)
is simply
G(x
-
y).
This is clearly wrong, as Examples 20.3.5 and 20.3.6 showed. The reason is,
of
course, the BCs. The fact that G(x - y) satisfies the right DE does not guarantee
that it also satisfies the right BCs. The following example, however, shows thatthe
conjecture is true for a homogeneous
initial
value
problem.
20.3.8.
Example.
Themoslgeneralfonn for the OF is
G(
{
CI UI(X) +C2U2(x)
if
a
~
x < Y,
x,y)
=
dlul(x)
+d2U2(x)
if
Y < x
~
b.
TheIVP conditionG(a, y) = 0 =
G'(a,
y) implies
CIUI(a)
+c2u2(a)
= 0
and
Linear
independence
of Ul andU2
implies
(
UI (a) U2(a»)
det
u;(a)
ui(a)
= W(a;
uI,
U2) ""
O.
Hence,
C1
= C2 = 0 istheonly
solution.
Thisgives
(20.37)
{
o
ffa5x<y,
G(x,
y) =
dIUI(X)
+d2U2(x)
if
y < x
~
b.
Continuity of G at x = y yields
dlUI
(y) + d2U2(y) = 0, while the discontinuity jump
conditionin thederivative gives
diU;
(y) +d2ui(Y) = I. Solvingthese twoequations, we
get
(20.38)
U;(Y)U2(Y) -
ui(y)uI
(y)'
d2=
dl
= U2(Y) ,
U;(Y)U2(Y) -
ui(y)uI(Y)
Substituting thisin (20.37)gives
G(x,
y) = [U2(Y)UI(x) - UI(Y)U2(X)]
e(x
_ y).
u; (Y)U2(Y) -
ui(y)uI
(y)

574 20.
GREEN'S
FUNCTIONS
IN
ONE
OIMENSION
Equation
(20.38)
holdsfor any
SOLDO
withthe givenBes. Wenowusethe factthatthe
SOLDO
hasconstantcoefficients. In thatcase,weknowtheexactformof
zej
and"2.
There
are
twocasesto
consider:
1.
If
the characteristic polynomial
of
Lxhastwodistinctroots Al and
}..2,
thenUl (x) =
e
AtX
and
U2(X)
= e
A2X
.
Writing
Al = a +b
and)..2
= a - b and
substituting
the
exponential
functions
andtheir
derivatives
in
Equation
(20.38)yields
[
eCa- b)Ye ca+b)X _
e(a+b)ye(a-b
h]
G(x,
y) = 2be
2ay
e(x
- y)
=
2~
[e(a+b)(X-y) -
e(a-b)(x-Y)j
e(x
- y),
whichis a
function
of x - y alone.
2.
If
Al = ).2 =
A,
then
Ul(X)
= e
Ax
,
u2(x)
= xe
Ax
,
and
substitution
of these
functions
in
Equation
(20.38)
gives
G(x,
y) =(x -
y)e'(x-Y)e(x
- y).
20.3.3 Inhomogeneous
Bes
III
GF
solves
inhomogeneous
BCs
as
well
So far we have concentrated on problems with homogeneous BCs, Ri [u] = 0,
for i =
1,2.
What
if
the BCs are inhomogeneous?
It
turns out that the Green's
function method, even though it was derived for homogeneous BCs, solves this
kind
of
problem as well! The secret
of
this success is the generalized Green's
identity.
Suppose we are interested in solving the DE
Lx[u] =
f(x)
with
Ri[U] = Yi
for i =
1,2,
and we have the GF for
Lx
(with homogeneous BCs,
of
course). We can substitute
v =
g(x,
y) =
G*(y,
x) in the generalized Green's identity and use the DE to
obtain
l
b
w(x)G(y,
x)f(x)
dx -l
b
w(X)u(x)(Lr[gj)*
dx =
Q[u,
g*(x,
Y)]I;~~,
or, using
d[g(x,
y)]
= 8(x -
y)/w(y),
u(y)
= t
w(x)G(y,
x)f(x)
dx
- Q[u,
g*(x,
Y)]I;~~.
To evaluate the surface term, let us write the BCs iu matrix form [see Equation
(20.17)]:
AU
a
+BUb = Y '* Ub =
B-Iy
-
B-IAu
a
,
AG
a
+BGb = 0 '* A'(B')-IOb9); +
Oa9;
= 0,
(

20.3
GREEN'S
FUNCTIONS
FOR
SOlOOS 575
where Y is a column vector composed
of
YI
and
Y2,
and we have assumed that
G(x,
y) and
g*(x,
y) satisfy, respectively, the homogeneons BCs (with Y = 0)
and their adjoints. We have also assumed that the 2 x 4 matrix of coefficients has
rank 2, and withontloss of generality,let Bbe the invertible 2 x 2 submatrix. Then,
assuming the general form
of
the surface term as in Equation (20.15), we obtain
Q[
*(
)][x~b
to * to *
u,g
x,Y
x=a=ub
b9b-ua
aga
(
-I -I
A)'
a * t *
= B Y - B U
a
b9b - u
a
Q
a
9
a
=
y'(B,)-I
Ob9);
-
U~,[At(B')-IOb9);
+Oa9~]
= 0
because
g*
satisfies
homogeneous
adjoint
Be
(20.39) .
where
* (
g*(b,
y) ) (
G(y,
b) )
gb
sa a * = a .
ax
g
(x, y)[x=b
axG(y,X)[x~b
It follows that
Q[u,
g*(x,
Y)]I;'~~
is given entirely in terms of G, its derivative, the
coefficient functions
of
the DE (hidden in the matrix
0),
the homogeneous BCs
(hidden in B), and the constants
YI
and
Y2.
The fact that g* and
agO
lax
appear
to be evaluated at
x = b is due to the simplifying (but harmless) assumption that
Bis invertible, i.e., that
u(b)
and
u'(b)
can be written in terms of
ural
and
u'(a).
Of course, this may not be possible; then we have to find another pair of the four
quantities in terms of the other two, in which case the matrices and the vectors
will change but the argument, as well as the conclusion, will remain valid. We can
now write
u(y)
= l
b
w(x)G(y,x)j(x)dx
_
ytM9*,
(20.40)
where ageneralmatrix Mhas beenintroduced, and the subscript
bhas beenremoved
to encompasscaseswhere submatricesotherthan Bare invertible. Equation (20.40)
shows that
u can be determined completely once we know
G(x,
y),
even though
the BCs are inhomogeneous.
In practice, there is no need to caicolate
M.
We can (
use the expression for
Q[u, gO] obtained from the Lagrange identity
of
Chapter
13 and evaluate it at
b and a. This, in general, involves evaluating u and G and
their derivatives at
a and b. We know how to handle the evaluation
of
G because
we can actually constroct it
(if
it exists). We next find two of the four' quantities
corresponding to
u in terms of the other two and insert the result in the expression
for
Q[u,
gO].Equation (20.39) then guaranteesthat the coefficientsof the othertwo
terms will be zero. Thus, we
can
simply drop all the terms in
Q[u,
gO]containing
a factor of the other two terms.

(20.41)
576
20.
GREEN'S
FUNCTIONS
IN
ONE
OIMENSION
Specifically, we
use
the
conjunct
for
a formally self-adjoint
SOLDO
[see Equa-
tion (20.26)]
and
g*(x,
y) =
G(y,
x)
to
obtain
u(y)
= l
b
w(x)G(y,x)f(x)dx
{
du
eo
]}X~b
-
p(x)w(x)
[G(y,
x)
dx
-
u(x)h(y,
x)
x~a
Intercbanging x
and
y gives
u(x)
= l
b
w(y)G(x,
y)f(y)
dy
{
[
eo
du]}Y=b
+
p(y)w(y)
u(y)-a
(x,
y) -
G(x,
y)-d
y y y=a
This
equation is valid only
for
a self-adjoint
SOLDO.
That
is,
using
it requires
casting
the
SOLDO
into a self-adjoint
form
(a process
that
is always possible, in
light
of
Theorem
13.5.4).
By
setting
f(x)
= 0, we
can
also
obtain
the
solution to a homogeneous
DE
Lx[u] = 0
that
satisfies
the
inhomogeneous
Bes.
20.3.9. Example. Let us findthe solution of the simpleDE d
2u/dx
2
=
f(x)
subjectto
the simple inhomogeneousBCs
u(a) =
Yl
and u(b) =
Y2.
The GF for this problem has
been calculatedin Examples20.1.5 and 20.3.5.Let us begin bycalculating the surfaceterm
in Equation (20.41).Wehave
p(y)
= I, and we set w(y) = I, then
surfaceterm
= u(b) oG I -
G(x,
b)u'(b) - u(a) oG I + G(x, a)u'(a)
oy
y=b
oy
y~a
=
Y2
oG I - Yl oG I + G(x, a)u'(a) - G(x, b)u'(b).
oy
y~b
oy
y~a
That
the
unwanted
(and
unspecified)
terms
are
zerocanbeseenby
observing
that
G(x,
a) =
g*(a, x) =(g(a, x))*, and that g(x, y) satisfiesthe BCsadjointto the homogeneous BCs
(obtained when
Yt = 0). In this particular and simple case, the BCs happen to be self-
adjoint (DirichletBCs). Thus,
u(a) =u(b) =0 implies that g(a, x) = g(b, x) =0 for all
x E [a, b]. (In amore
general
casethecoefficient
ofu'(a)
wouldbemore
complicated,
but
still zero.) Thus, we fioallyhave \
surfaceterm
=
Y2
oG I - Yl oG I .
oy y=b oy y=a
Now,using the expressionfor G(x, y) obtained in Examples 20.1.5 and 20.3.5,we get
8G
a-x
x-a
- =
---
- 9(x - y) - (x - y)8(x - y) =
--
- 8(x -
y).
oy
b-a
"
b-a
=0
Thus,
soI
x-a
BY
y=b =
b-a'
OGI
x
-a
x - b
-
----1---
oy y=a -
b-a
-
b-a'

20.4
EIGENFUNCTION
EXPANSION
OF
GREEN'S
FUNCTIONS
577
Substituting in Equation
(20.41),
we get
u(x) = f
G(x,y)f(y)dy
+
~=~IX+
bY~=:Y2.
(Compare
thiswiththeresultobtainedin Example
20.1.5.)
III
Green's functions have a very simple and enlighteningphysical interpretation.
AninhomogeneousDE such as
Lx[u]
=
f(x)
can be interpretedas ablackbox
(L,)
that determines a physical quantity (u) when there is a source
(f)
of that physical
quantity. For instance, electrostatic potential is a physical quantity whose source
is charge; a magnetic field has an electric current as its source; displacements and
velocities have forces as their sources; and so forth. Applying this interpretation
and assuming that
w(x)
= 1, we have
G(x,
y)
as the physical quantity, evaluated
at
x when its source 8(x - y) is located at y. To be more precise, let us say that
the strength of the source is
81
and it is located at Yl; then the source becomes
818(x -
Yl).
The physical quantity, the Green's function, is then 81G(X,
Yl),
because of the linearity of Lx:
If
G(x,
y) is a solution of
Lx
[u] = 8(x - y), then
81
G(x,
Yl)
is a solution of
Lx[u]
= 818(x -
y).
If
there are many sources located
at
{yil[:,1
with corresponding strengths {8il[:,1' then the overall source f as a
function of
x becomes
f(x)
=
L,[:,t
8i8(X - Yi), and the corresponding physical
quantity
u(x)
becomes
u(x)
=
L,[:,1
8iG(X,
Yi).
Sincethe source S; is located at Yi, it is more natural to define a function 8
(x)
and write S; = 8(Yi). When the number
of
point sources goes to infinity and Yi
becomes a smoothcontinuous variable, the sumsbecome integrals,
and-
we have
f(x)
= l
b
8(y)8(x
- y)
dy,
u(x)
= l
b
8(y)G(x,
y)
dy.
The first integral shows that 8
(x)
= f
(x).
Thus, the second integral becomes
u(x)
=
J:
f(y)G(x,
y) dy which is precisely what we obtained formally.
20.4 Eigenfunction Expansion
of
Green'sFunctions
Green'sfunctions areinversesof differential
operators.
Inverses
of
operators
in a
Hilbert space are best studied in terms of resolvents. This is becauseif an operator
Ahasaninverse, zerois initsresolventset, and
Thus,
it is
instructive
to discuss
Green's
functions
in thecontext of theresolvent
of a differential operator. We will cousider only the case where the eigenvalues are
discrete, for example, when Lxis a Sturm-Liouville operator.
Formally, we have
(L - A
l)R)JL)
= 1, wbich leads to the DE
8(x - y)
(Lx - A)R).(x, y) = ,
w(x)

(20.42)
578 20.
GREEN'S
FUNCTIONS
IN
ONE
DIMENSION
where R).(x, y) = (xl R,,(L)ly). The DE simply says that R,,(x, y) is the
Green's function for the operator
Lx
-
A.
So we can rewrite the equation as
a, - A)G,,(X, y) =
8(x
-
y)jw(x)
where
Lx
- A is a DO having some ho-
mogeneous BCs. The GF G"
(x,
y) exists
if
and only
if
(Lx - A)[u] = 0 has no
nontrivial solution, which is true only if
Ais not an eigenvalue
of
Lx.We choose
the BCs in such a way that
Lx
becomes self-adjoint.
Let
{Anl~l
be the eigenvalues of the system
Lx[u]
= AU, {Ri[U] =
OIT=l'
and let the
u~k)
(x)
be the corresponding eigenfunctions. The index k distinguishes
among the linearly independent vectors corresponding to the same eigenvalue
An.
Assuming that Lhas compact resolvent (e.g., a Sturm-Liouville operator), these
eigenfunctions form a complete set for the subspace of the Hilbert space that
consists of those functions that satisfy the same BCs as the
u~k)
(x). In particnlar,
G,,(x,
y) can be expanded in terms of
u~k)(x).
The expansion coefficients are,
of
course,functions of y. Thus,we can write
00
G,,(x,
y)
= L
~>~k)(y)u~k)(x)
k
n=l
where
a~k)(y)
=
J:
w(x)u~(k)(x)G,,(x,
y)
dx.
Using Green's identity, Equation
(20.30), and the fact that
Anis real, we have
b .
Ana~k)(y)
= 1
W(X)[AnU~k\X)]'G,,(x,
y)dx
= l
b
w(x)G).(x,
y){Lx[u~k)(x)]}·
dx
= l
b
w(x)[u~k)(x)]'Lx[G,,(x,
y)]
dx
= l
b
w(x)u~(k)(x)
[8(X
-
y)
+AG,,(X,
y)]
dx
a
w(x)
=
u~(k)(y)
+Al
b
w(x)u~(k)(x)G).(x,
y)
dx
=
u~(k)(y)
+
Aa~k)(y).
Thus,
a~k)(y)
=
u~(k)(y)j(An
- A), and the expansionfor the Green's function is
G ( )
_
'"
~
u~(k)(y)u~k\x)
" x, y - L... L... A _ A .
k
n=l
n
This expansion is valid as long as An
i'
A for any n = 0, I, 2,
....
But this is
precisely the condition that ensures the existence of an inverse for L-
A1.
An interesting result is obtained from Equation (20.42)
if
A is considered a
complex variable.
In that case, G" (x,
y)
has (infinitely many) simple poles at

20.4
EIGENFUNCTION
EXPANSION
OF
GREEN'S
FUNCTIONS
579
{A"}~l'
The residue at the pole A" is -
Lk
u:(k)(y)u~k)(x).
If
c; is a contour
having the poles
{A"};:'=l in its interior, then, by the residue theorem, we have
In particular, if we let
m
-+
00,
we obtain
S(x -
y)
w(x)
,
(20.43)
where Coo is
any contour that encircles all the eigenvalues, and in the last step
we used the completeness
of
the eigenfunctions. Equation (20.43) is the infinite-
dimensional analogue
of
Equation (16.12) with f (A) = 1 whenthe latterequation
is sandwiched between
(x Iand I
y).
20.4.1.
Example.
Consider the DO Lx = d
2/dx
2
with BCs u(O) =
ural
=
o.
This is
an S-L operator with eigenvalues and normalized eigenfunctions
_
(mr)2
An-
-
a
and
(2 .
(mr
)
Un(X)=v~sm
aX
for n = 1,2,
....
Equation (20.42) becomes
G
x
__
~
~
sin(mrx/a)
sin(mry/a)
)J ,y) -
L.
'(
/)2
a
n=l
I\,
- n1f a ,
which leads to
1 i
()d
1 i [2
~
sin(mrx/a)sin(mry/a)]
d
-
G,
x Y A=-
--
L.
A
2rri
Coo
'.
2:rri Coo a
n=l
A-
(mrja)2
=
__
1
(~)
I:sin
(mr
x)
sin
(""
y)
1.
dA
2:Jr:i
a
n=l
a a ie
oo
A-
(nJrja)2
= _
(~)
f:sin
(n"
x)
sin
(n"
y)
Res [ 1
2]
a
n=l
a a ').-
(mf/a)
l=A
n
= -
(~)
f:
sinC"
x)
SinC"
y).
a n=l a a
eigenfunclion
expansion
of
GF
The RHS is recognized as
-8(x
- y).
If
zero is not an eigenvalue
of
Lx, Equation (20.42) yields
00
u:(k)(y
)u~k)
(x)
G(x,y)=Go(x,y)=LL
'
k
n=l
An
(20.44)
which is an expression for the Green's function
of
Lx in terms
of
its eigenvalues
and eigenfunctions.

580 20.
GREEN'S
FUNCTIONS
IN
ONE
OIMENSION
20.5 Problems
20.1. Using the GF method, solve the DE
Lxu(x)
=
duf
dx
=
f(x)
subject to
the BC
u(O) =a. Hint: Consider the function
vex)
=
u(x)
- a.
20.2. Solvethe problem of Example 20.1.4 subjectto the BCs
u(a)
=
u'(a)
=
O.
Show that the corresponding GF also satisfies these BCs.
20.3. Show that the IVP with data 10;0, 0,
...
,
OJ
has only u
'"
0 as a solution.
Hint: Assume otherwise, add
u to the solution
of
the inhomogeneous equation,
and invoke uniqueness.
20.4.
In this problem, we generalize the concepts
of
exactness and integrating
factor to a NOLDE. The DO
Lin)
es
I:~=o
pkCx)d
k
/dx
k
is said to be exact if
there exists a DO Min-I) sa
I:~;;6
ak(x)d
k
/dx
k
such that
VUE
en[a, b].
(a) Show that
Lin)
is exact iff
I:~~o(
_I)md
m
Pm/dxm
=
O.
(b) Show that there exists an integrating factor for
Lin)-that
is, a function
/L(x)
such that /L(x)Li
n)
is
exact-if
and only
if
/L(x)
satisfies the DE
The DO Ni
n)
is the formal adjoint
of
L¥').
20.5. Assuming that
Lx[u]
= 0 has no nonttivial solution, show that the matrix
where UI and
U2 are independent solutions
of
Lx[u]
= 0 and Ri are the bound-
ary functionals, has a nonzero determinant. Hint: Assume otherwise and show
that the system of homogeneous linear equations
aRI[uI]
+
,BRI[U2]
= 0 and
aR2[u!l
+,BR2[U2] = 0 has a nontrivial solution for
(a,,8).
Reacha contradiction
by considering
u =
aUI
+,Bu2as a solution of
Lx[u]
=
O.
20.6. Determine the formal adjoint of each
of
the operators in (a) through (d)
below (i) as a differential operator, and (ii) as an operator, that is, including the
BCs. Whichoperatorsare formally self-adjoint?Whichoperators are self-adjoint?
(a)
Lx = d
2/dx
2
+I in [0, 1] with
BC,
u(O) =
u(l)
=
O.
(b) Lx = d
2/dx
2
in [0, 1]
withBCs
u(O) = u'(O) =
O.
(c) Lx = df
dx
in [0, 00]
withBCs
u(O) =
O.
(d) Lx = d
3/dx
3
-
sinxd/dx
+3 in [0, IT] with BCs u(O) =
u'(O)
= 0,
u"(O)
-
4u(IT)
=
O.
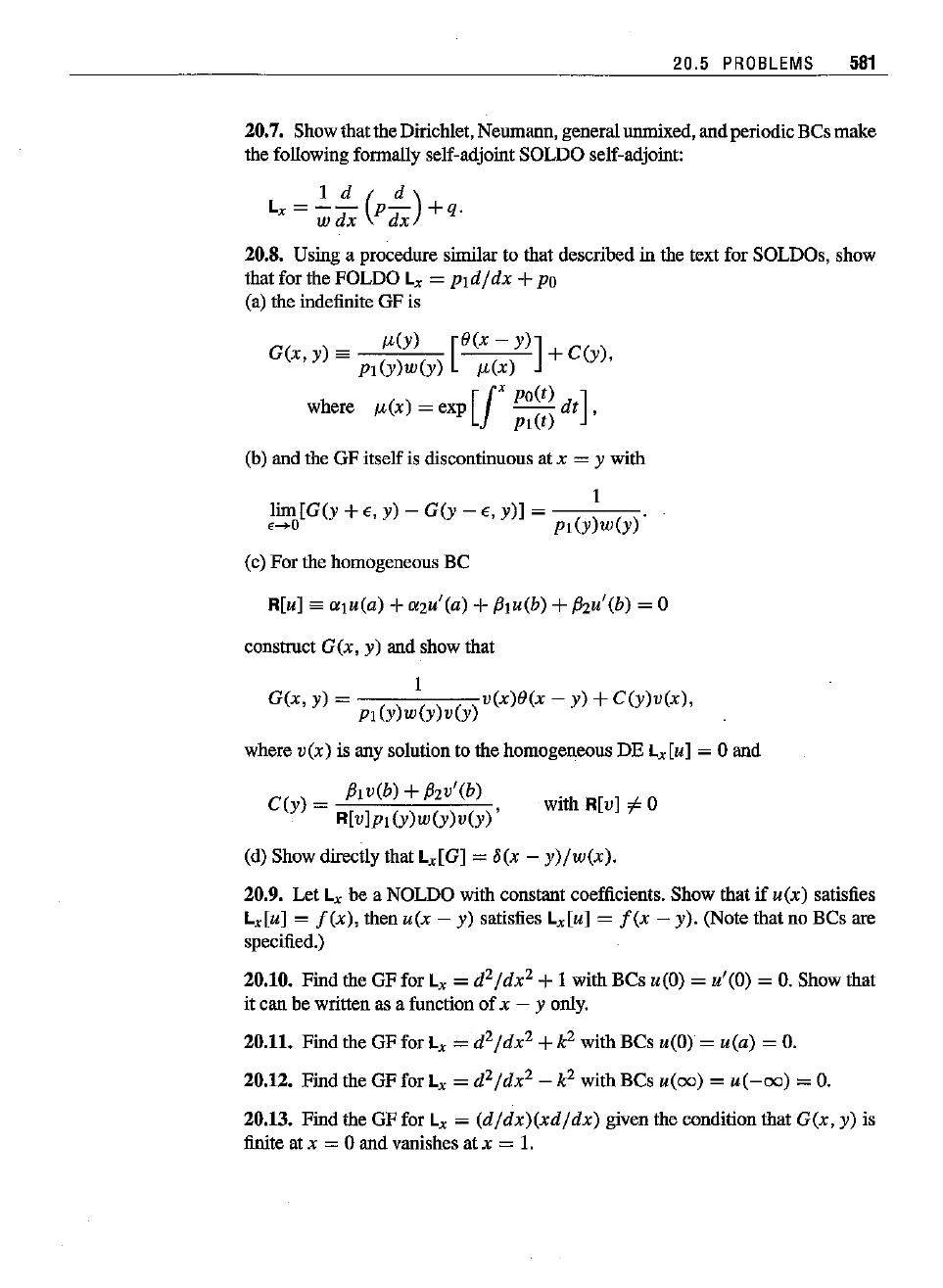
with R[v]
01
0
20.5
PROBLEMS
581
20.7. Show that the Dirichlet, Neumann, generalumnixed, and periodicBCs make
the following formally self-adjoint SOLDO self-adjoint:
Lx
=.!..~
(p~)
+q.
wdx
dx
20.8. Using a procedure similar to that described in the text for SOLDOs, show
that for the FOLDO
Lx
= PI dj dx +
PO
(a) the indefinite GF is
G(x,
y) sa
{'(y)
[e(x
-
y)]
+
C(y),
PI(Y)w(y)
{'(x)
[I
X
po(t)
]
where
{'(x)
= exp
--
dt
,
PI(t)
(b) and the GF itselfis discontinuous at x = y with
. 1
Inn
[G(y
+E, y) -
G(y
- E,
y)]
=
()
()'
,-+0
PI Y w Y
(c)
For
the homogeneous BC
R[u] sa
O<lu(a)
+
0<2u'(a)
+f3tu(b) +
fhu'(b)
= 0
construct
G(x,
y) and show that
I
G(x,
y) =
()
()
( ) v
(x)e
(x - y) +
C(y)v(x),
PI Y w Y v Y
where
v(x)
is any solution to the homogeneous DE Lx[u] = 0 and
C(y)
=
f!(v(b)
+
{hv'(b)
,
R[v]PI
(y)w(y)v(y)
(d) Show directly that Lx[G] =
~(x
-
y)jw(x).
20.9. Let Lx be a NOLDO with constant coefficients. Show that
if
u(x)
satisfies
Lx[u] =
f(x),
then
u(x
- y) satisfies Lx[u] =
f(x
-
y).
(Note that no BCs are
specified.)
20.10. Find the GF for
Lx
=d
2
jdx
2
+1 with BCs u(O) =u'(O) =
O.
Show that
it can be written as a function of
x - y only.
20.11. Find the GF for Lx =d
2
jdx
2
+k
2
withBCs u(O) =
u(a)
=
O.
20.12. Find the GF for Lx =d
2
jdx
2
- k
2
with BCs u(oo) =
u(-oo)
=
O.
20.13. Find the GF for
Lx
=
(djdx)(xdjdx)
given the condition that
G(x,
y) is
finite at
x = 0 and vanishes at x = I.

582 20.
GREEN'S
FUNCTIONS
IN
ONE
DIMENSION
20.14. Evaluate the GF and the solutions for each of the following DEs in the
interval [0, I].
(a)
u" - k
2
u =
f;
u(O) - u'(O) = a,
u(l)
= b.
(b) u" =
f;
u(O) = u'(O) = O.
(c) u" +6u' +9u = 0; u(O) = 0, u'(O) = 1.
(d)
u" +!J)2u =
f(x),
for x > 0; u(O) = a, u'(O) = b.
(e) u(4) =
f;
u(O) = 0, u'(O) =
2u'(I),
u(l)
= a, u"(O) =
O.
20.15. Use eigenfunctionexpansion
of
the GF to solve the BVP u" =
x,
u(0) =0,
u(l)
-
2u'(I)
=
O.
Additional Reading
I. Dennery, P.and Krzywicki,A. Mathematicsfor Physicists, Harperand Row,
1967. Contains an exposition
of
Green's functions for second-order linear
differential equations.
2. Roach, G.
Green's Functions, Van Nostrand, 1970. A readable introduc-
tion to Green's functions, especially those we have called "indefinite" (no
bonndary conditions specified).
