Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


(11.24)
11.5
METHOD
OF
STEEPEST
DESCENT
313
be helpful
if
we could find a general approximation for it that is applicable for
all f and g.
The
fact that
lal
is large will be
of
great help. By redefining
f(z),
if
necessary, we can assume that
a =
lale'
arg(a) is real and positive [absorb e'
argte)
into the function
f(z)
if
needbe].
The exponent
of
the integrand
can
be written as
af(z)
=
au(x,
y) +
iav(x,
y).
Since a is large and positive, we expect the exponential to be the largest at the
maximum
of
u(x,
y). Thus, if we deform the contour so that it passes through a
point zo at which
u(x, y) is maximum, the contribution to the integral may come
mostly from the neighborhood
of
zoo
This opens up the possibility
of
expanding
the exponent about zo and keeping the lowest terms in the expansion, which is
what we are after. There is one catch, however. Because
of
the largeness
of
a, the
imaginary part
of
af
in the exponent will oscillate violently as
v(x,
y) changes
even by a small amount. This oscillation can make the contribution
of
the real
part
of
f(zo)
negligibly small and render the whole procedure useless. Thus, we
want to tame the variation
of
exp[iv(x,
y)] by making
v(x,
y) vary as slowly as
possible. A necessary condition is for the derivative
of
v to vanish at
zoo
This and
the fact that the real part is to have a maximum at zo lead to
au . av
dfl
ax +Z ax =
dz
zo
=
o.
However, we do not stop here
but
demandthatthe imaginary part
of
f be constant
along the deformed contour:
Im[f(z)]
=
Im[f(zo)]
or
v(x,
y) =v(xo, Yo).
Equation (11.24) and the Cauchy-Riemann conditions imply that
aujax
=
0=
aujay
atzo.
Thus, it might appearthatzo is a maximum (or minimum)
of
the
surface described by the function
u(x,
y). This is not true: For the surface to have
a maximum (minimum), both second derivatives, a
2ujax
2
and a
2uja
y2, must be
negative (positive). But thatis impossiblebecause
u(x, y) is
harmonic-the
sum
of
these two derivatives is zero. Recall that a pointat whichthe derivatives vanish
but
that is neither a maximum
nor
a minimumis called a saddlepoint. That is why the
procedure described below is sometimes calledthe
saddle
point
approximation.
We are interested in values
of
z close to zo. So let us expand
f(z)
in a Taylor
series about zo, use Equation (11.24), and keep terms only up to the second, to
obtain
f(z)
=
f(zo)
+
!(z
- ZO)2I"(zo).
Let
us assume that
t"
(zo)
f=
0, and define
z - zo
=
Yje
iB,
and
!f"(zo)
= T2eifh
and substitute in the above expansion to obtain
f(z)
-
f(zo)
=
TfT2ei(2Bz+fh),
(11.25)
(11.26)
(11.27)

314 11.
COMPLEX
ANALYSIS:
ADVANCED
TOPICS
y
z,t>~O
__
Co
x
Figure11.12 A
segment
ofthe
contour
Coin thevicinityof
zoo
Thelines
mentioned
in
thetextaresmall
segments
ofthe
contour
Co
centered
at
zoo
or
Re[f(z)
- f(zo)] =
rhcos(201
+02),
Im[f(z)
- f(zo)] = rrr2 sin(
2
01
+
~).
(11.28)
The constancy of
Im[f(z)]
implies that sin(201 +02) = 0, or 201 +
02
=
ntt
.
Thus, for
01
=
-~/2
+nIT
/2
where n = 0, I, 2, 3, the imaginary part of f is
constant. The angle
02
is determined by the second equation in (11.26). Once we
determine n, the path
of
saddle pointintegration will be specified.
To get insight into this specification, consider z - zo =
rle
i(-1J,/2+nrr/2),
and
eliminate rl from its real and imaginary parts to obtain
y-yo=[tanC;
-~)](X-xo).
This is the equation of a line passing through zo = (xo,
YO)
and making an angle
of
01 = (nIT -
~)/2
with the real axis. For n =
0,2
we get one line, and for
n =
1,3
we get another that is perpendicular to the first (see Figure 11.12).
It
is
to be emphasized that along both these lines the imaginary part
of
fez)
remains
constant. Tochoose the correctline, we need to lookat the real part of the function.
Also note that these "lines" are small segments
of
(or tangents to) the deformed
contourat
zoo
Weare lookingfor directions along which
Re(f)
goes through a relative max-
imum at
zoo
In fact, we are after a path on which the function decreases maximally.
This occurs when
Re[f(z)]
-
Re[f(zo)]
take the largest negative value. Equation
(11.28) determines such a path:
It
is that path on which cos(20
1
+02) =
-I,
or
when
n =
1,3.
There is ouly one suchpath in the region
of
interest, and the pro-
method
of
steepest
cedure is uniquely determined/' Because the descent from the maximum value at
descent

11.5
METHOO
OF
STEEPEST
OESCENT
315
zo is maximum along such a path, this procedure is called the method
of
steepest
descent.
Now that we have determined the contour, let us approximate the iutegral.
Substituting 2ej
+
e2
=
tt,
3n in Equation (11.27), we get
fez)
-
f(zo)
=-rir: es
_t
2
=
i(z
-
ZO)2
f"(zo).
Using this in Equation (11.23) yields
I
(a)
""
(
ea[i(zoH']
g(z)
dz
= e
ai
C,
o)
(
e-
a
t'
g(z)
dz,
leo
leo
(11.29)
(11.30)
where Co
is
the deformed contour passing through
zoo
To proceed, we need to solve for z in terms
of
t. From Equation (11.29) we
have
2 2 2 t
2
-ie,
(z - zo) =
---I
=
--e
!"(zo)
ri
Therefore, [z - zoI=It
1/
JT2,
or Z - zo =(It
1/
JT2)e
ie
"
by the first equation
of
(11.26). Let us agree that for t > 0, the point z ou the coutour will move in the
direction that makes an angle
of
0 :5
el
<
tt
, and that t < 0 correspouds to the
opposite direction. This conventionremoves the remaining ambiguity
of
the angle
el,
and gives
1 ·0
z=zo+-e
l 1
,
JT2
(lUI)
Using the Taylor expansion
of
g(z)
about zn, we can write
g(z)dz
=
{~~einOlg(n)(zO)}
e
i
O,
dt
L.-
n/2 I 'ri.
n=O 7
2
n.
'V':l.
00
tn
= "
ei(n+I)01
g(n\ZO)
dt
L-
(n+l)/2
, I
n=O 7
2
n.
and substituting this in Equation (11.30) yields
I(a)
""
eaiC.o) {
e-
at'
{~
t
n
eiCn+I)O,
gcn)(ZO)}
dt
lee
L.-
Cn+I)/2 ,
o n=O 7
2
n.
00
i(n+l)91
JOO
= eaiC'o)" e g(n)
(ZO)
e-at't
n
dt.
L.-
Cn+I)/2 ,
n=O 7
2
n.
-00
(11.32)
5Theangle
191
is still
ambiguous
by
x,
becausen canbe 1or3.
However,
by asuitablesign
convention
described
below,we
canremovethis
ambiguity.

316
11.
COMPLEX
ANALYSIS:
ADVANCED
TOPICS
The extension of theintegral limits to infinitydoes not alter the result significantly
because a is assumed large and positive. The integral in the sum is zero for odd n.
Whenn
iseven, wemakethe substitutionu =
at
2
and showthat
J~oo
e-
at2
t"dt =
a-(n+l)/2r[(n+
1)/2].
Withn
=
2k,
andusing r2 = I
f"(zo)
1/2,thesumbecomes
asymptotic
expansion
ofI(a)
00
2k+l/2 i(2k+I)el
[(a)
"" ea!(,o)
'"
e g(2k)
(zo)r(k
+
!)a-
k-
1/2.
f;;o
If"(zo)lk+l/2(2k)!
2
(11.33)
(11.34)
(11.35)
III
Stirling
approximation
This is called theasymptotic expansion of
[(a).
In most applications, only the
firstterm of the above series is retained, giving
[(ex) "" ea!(,o)
fiIT
eiel
g(zo)
.
V
-;-
JI
f"
(zo)1
11.5.1. Example. LeI us
approximale
the
integral
[(ex)
==
r(ex +1) =
faOO
e-,zadz,
where
ex
is a positivereal number. First, we
must
rewritethe integralin the
fonn
of
Equation
(11.23).
We
candothisby
noting
that za =e
alnz.
Thus,we
have
l(ex) =
10
00
ealnZ-Zdz
=
10
00
elX(lnz-z/a)dz,
and
We
identify
f(z)
=ln z-
z/a
andg(z) =
I.
The
saddle
pointis
found
from
f'(z)
= 0
or zu = C1. Furthermore, from
1 " 1 (
1)
1
in
2
f
(zn) = 2 - a
2
=
2cx
2e
and
2(h +
6z
=
x,
3n. as well as the condition 0
:::::
81 < zr, we conclude that 91 = O.
Substitution
in
Equation
(1
1.34)
yields
r(ex +1) ""
ea!(,o)
rzrr_
l
_
= .J2Jrexe
a(lna-l)
=
5e-
a
a
a
+l/
2
,
V-;;./1/ex2
called
theStirlingapproximation.
11.5.2. Example. TheHankel function
of
the first kind is
defined
as
HSI)(ex)
==,!-
( e(a/2)(,-1/zl..!!:.-,
lJr lc
zv+l
where C is the contour shown in Figure 11.13. We want to find the asymptotic expansion
of this function, choosing the branch
of
the function in which
-l'C
< e<
'Jr.
We
identify
f(z)
=
:!:(z
- I/z) and
g(z)
=
z-v-I.
Next,
the
stationary
points
of f
are calculated:
df
I I
dz
=
2:
+ 2z2 =0
=}
Zo = ±i.
11.5
METHOD
OF
STEEPEST
DESCENT
317
Irnz
in
1-----.-----
o
Rez
III
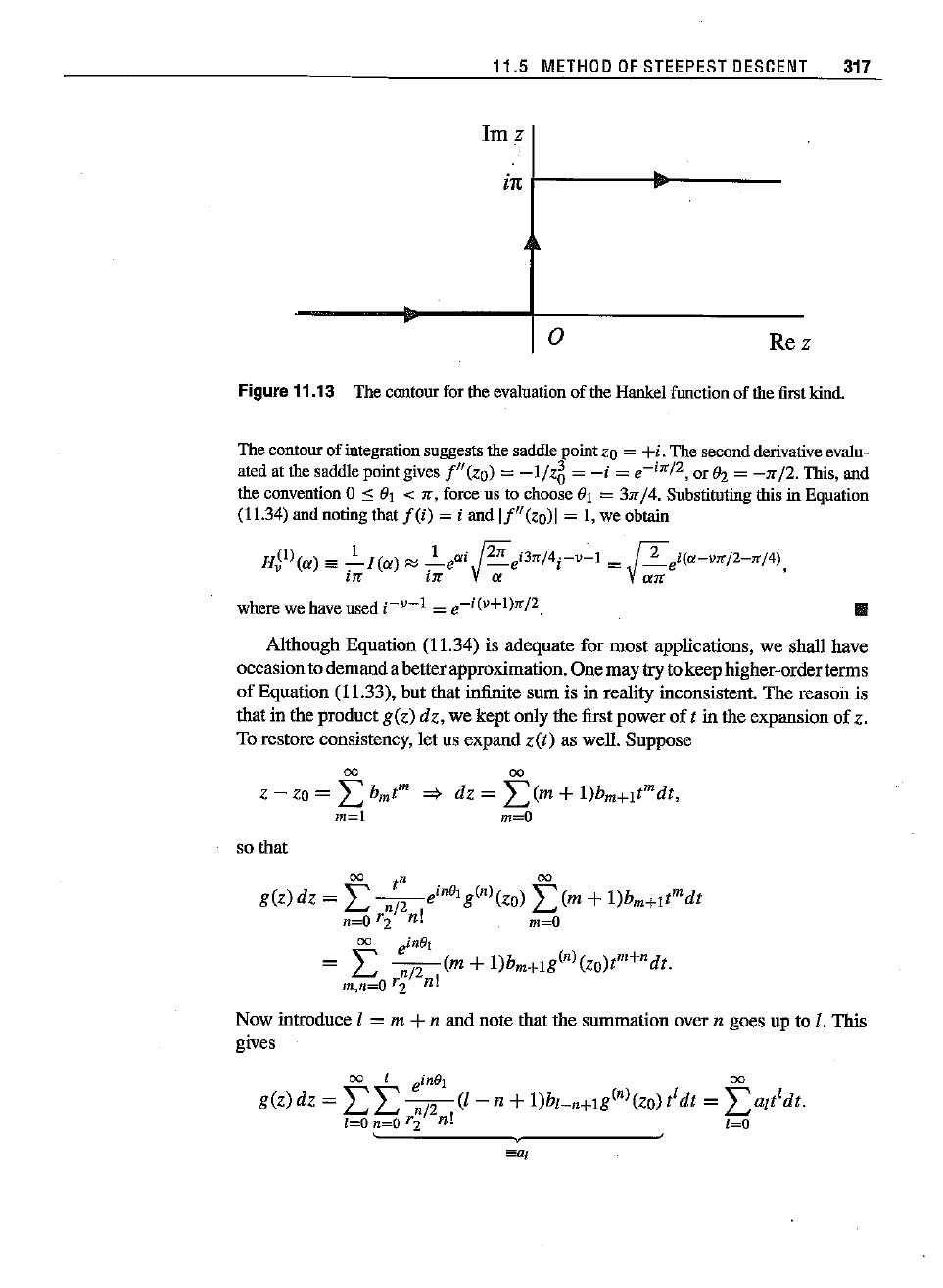
Figure 11.13 The contourfor the evaluation of the Hankelfunctionof thefirstkind.
The contour
of
integration suggests
the
saddle
point
ZQ = +i.
The
secondderivative evalu-
atedat the saddlepointgives
f"(zo)
= -1/z5 =
-i
=
e-
i
" j2, or Ih = -,,/2. This,and
the convention 0
:::::
611
<
1r,
force us to choose
611
=
3.1l"
/4. Substituting this in Equation
(11.34)andnotingthat
f(i)
= i and
II"(zo)1
= I, we obtain
H~l)(a)
es
~I(a)
~
~eai
fiJr
e
i3rr/4
i
- v- l =
(2ica-vlr/z-n/4),
IX
m V-;;
Van
where we have
used
i-
v
-
1
=
e-
i(v+l)rrj2.
Although Equation (11.34) is adequate for
most
applications, we shall have
occasionto demandabetterapproximation. One may try tokeephigher-orderterms
of
Equation (11.33), but that infinite sum is in reality inconsistent.
The
reason is
thatin the product
g(z)
dz; we
kept
only the first power
of
t in the expansion
of
z.
To restore consistency, let us expand
z(t)
as well. Snppose
00
z-zo
=
Lbmtm
m=l
so that
00
=}
dz
=
L(m
+
l)b
m+1t
mdt,
m=O
00
tn
00
g(z)
dz
= L
-;;72-/
no
,g(n)(zo)
L (m +
I)bm+ltmdt
n=O 7
2
n. m=O
00
e
in8r
= L
~(m
+
l)b
m+lg(n)(Zo)t
m+
ndt.
m,n=O T
2
n.
Now introdnce 1 = m +n and note that the summation over n goes np to I. This
gives

318 11.
COMPLEX
ANALYSIS:
ADVANCED
TOPICS
Substituting this in Equation (11.30) and changingthe contourintegration into the
integral from
-00
to
00
as before yields
00
I(a)
"" ea!(zo)
Lazka-k-I/Zr
(k
+!),
k~O
2k ein(h
au
= L
---nj2(2k
- n +l)bZk_n+lg(n)(zo).
n=O
r
2
n!
(11.36)
The only thing left to do is to evaluate
b
m
•
We shall not give a general formula
for these coefficients. Instead, we shall calculate the first three of them. This shonld
reveal to the reader the general method
of
approximating them to any order. We
have already calculated
bt in Equation (11.31). To calculate bz, keep the next-
highest term in the expansion
of
both z and t
Z
•
Thus write
t
Z
=
-~
f"(zo)(z
-
zo)z
-
~
f"'(zo)(z
- ZO)3.
2 6
Now substitute the first equation in the second and equate the coefficients of equal
powers of
t on both sides. The second power
of
t gives nothing new:
It
merely
reaffirms the value of
bl.
The coefficient of the thirdpower
of
t is
-bl
bzt"(zo) -
ibif"'(zo).
Setting this equal to zero gives
(11.37)
bz
=
bf
fill (zo) _ fill (zo) e
4i9
[
6f"(zo)
- 31f"(zo)12 ,
where we substituted for bl from Equation (11.31) and used
201
+
Oz
=
tt
.
To calculate b3,keep one more term in the expansion
of
bothz and t
Z
to obtain
and
2
1"
2 1 m 3 1 (iv) 4
t =
--
f (zo)(z -
zo)
- - f (zo)(z -
zo)
- - f (zo)(z -
zo)
2 6 24 .
Once again substitute the first equation in the second and equate the coefficients
of equal powers of
t on both sides. The second and third powers
of
t give nothing
new. Setting the coefficient of the fourth power of
t equal to zero yields
b _ b3 {
5[f"'(zo)]z
f(iV)}
3 - I 72[f"(zo)]Z -
24f"(zo)
../ie
3i9
[
{5[flll(zo)f
f(iV)}
= 121f"(zo)1
3
/
Z
3[f"(zo)]Z -
f"(zo)
.
(11.38)
11.6
PROBLEMS
319
Imz
2i1[;/'
+
__
---,
\..LJ
•
f\
-00
o
+00
Rez
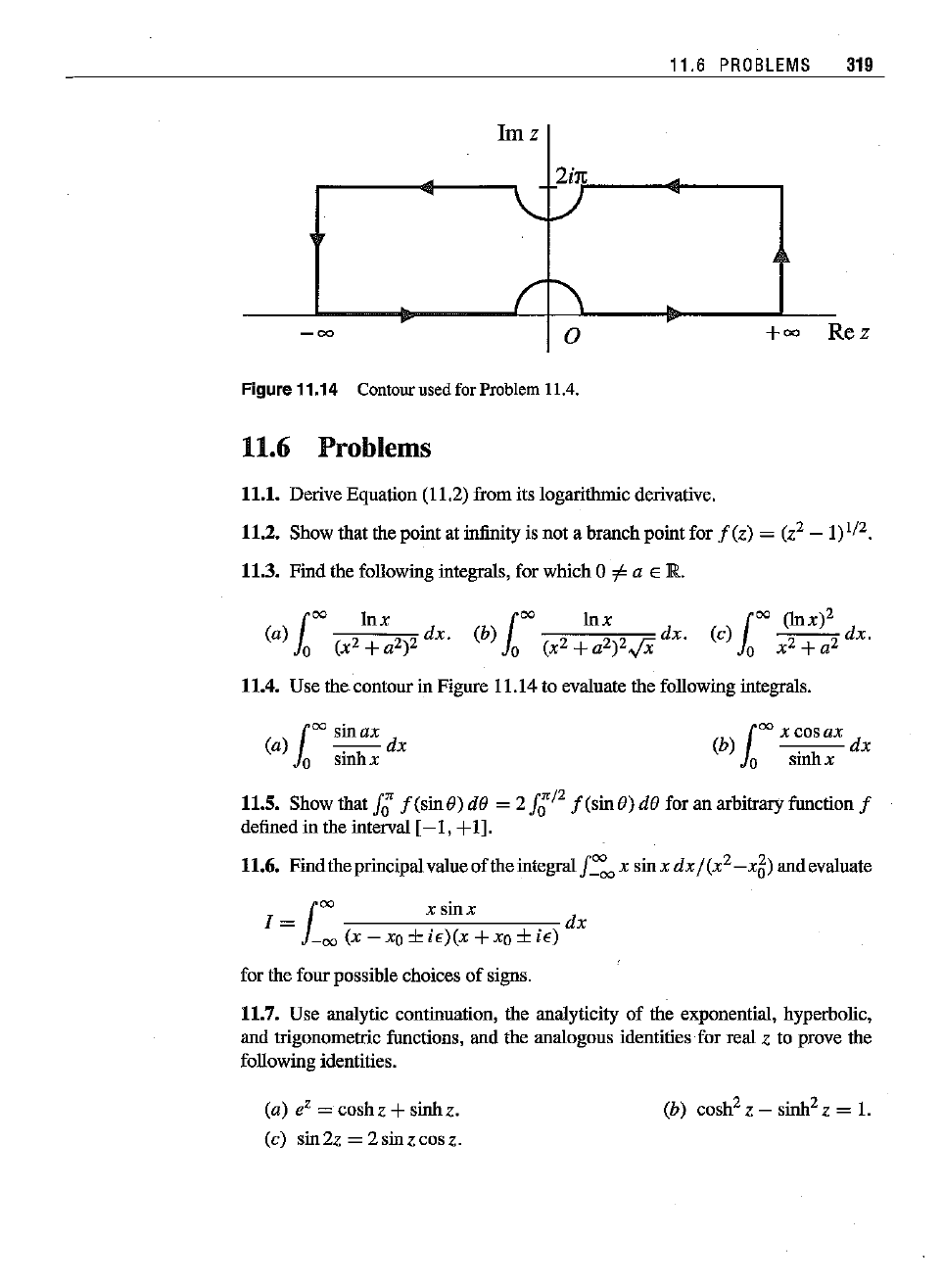
Figure 11.14 Contourused for Problem 11.4.
11.6 Problems
11.1. Derive Equation (11.2)
from
its logarithmic derivative.
11.2. Show that the
point
at infinity is
not
a
branch
point
for
f(z)
= (z2 - 1)1/2.
11.3.
Find
the following integrals, for
which
0
t=
a E R.
1
00
(lnx)2
(e)
22dx.
o x
+a
11.4.
Use
the contour in Figure 11.14 to evaluate the following integrals.
(a)
roo
s~ax
dx
Jo
sinhx
(b)
roo
x
~osax
dx
Jo
smhx
11.5. Show that1;
f(sine)
de
=
21;/2
f(sine)de
for an arbitrary function f
defiued iu the interval
[-I,
+1].
11.6.
Find
the principalvalue
of
the integral
1.':"00
x sin x
dx
/ (x
2
- x5)
and
evaluate
1
00
x sinx d
1=
x
-00
(x - xo ±
i€)(x
+Xo±
i€)
for the
four
possible choices
of
signs.
11.7. Use analytic continuation, the analyticity
of
the exponential, hyperbolic,
and trigonometric functions, and the analogous identities for real
z to prove the
following identities.
(a) e
Z
= cosh z +sinhz.
(e)
sin2z
=
2sinzcosz.
(b)
cosh
2
z - sinh
2
Z = 1.

320 11.
COMPLEX
ANALYSIS:
ADVANCED
TOPICS
11.8. Show that the function
I/z
2
represents the analytic continnation into the
domain
iC
-
{OJ
(all the complex plane minns the origin)
of
the function defined
by
L:~o(n
+
I)(z
+ I)" where [z+ II < 1.
11.9. Find the analytic continuation into
iC-
Ii,
-i}
(all the complexplane except
i and
-i)
of
f(z)
= fo
oo
e-
zt
sin t
dt
where Refz) >
O.
11.10. Expand
f(z)
=
L:~o
zn (defined in its circle of convergence) in a Taylor
series about z
= a. For what values of a does this expansion permit the function
f (z) to be continued analytically?
11.11. The two power series
00
zn
Ji(z)
=
L-
n=l
n
and
.
~
n (z
_2)n
!z(z)
=
in
+
L..(-I)
-'--'--------'-
n=l
n
and
where Retz)
>
O.
have no commondomain of convergence. Show that they are nevertheless analytic
continuations
of
one
another.
11.12. Prove that the functions defined by the two series
I (I -
a)z
(I - a)2
z2
-I
---z-
(I
-
Z)2
+
-'-(:-:-I-_--"Z"")3c-
are analytic continuations of one another.
11.13. Show that the function Ji(z) =
I/(z2
+
I),
where z
i'
±i, is the analytic
continuation into
iC
- Ii,
-i}
of
the function
!z(z)
=
L:~0(_l)nz2n,
where
lel
< 1.
11.14. Find the analytic continuation into
iC
-
{OJ
of
the function
f(z)
=
10
00
te-
zt
dt
11.15. Show that the integral in Equation (11.9) converges. Hint: First show that
[F'(z +
I)
I
::s
fo
oo
t
X
e-
t
dt
where x = Retz), Now show that
for some integer
n > 0
and conclude that
I'(z)
is finite.
11.16. Show that
dr(z
+
1)ldz
exists and is finite by establishing the following:
(a) [Inr] <
t+
lit
for t >
O.
Hint:
Fort:::
I,
showthatt
-Int
is a monotonically
increasing function. For t
< I, make the substitution t =
lis.
(b) Use the result from part (a) in the integral for
dr(z
+
1)ldz
to show that
Idr(z
+
I)ldzl
is finite. Hint: Differentiate inside the integral.

11.6
PROBLEMS
321
11.17. Derive Equation (11.11) from Equation (11.9).
11.18. Show that
I'
(~)
=
.ft,
and that
2
k
(2k+l)
(Zk -
I)l!
==
(Zk
-j)(2k
- 3)
..
·5·3·
I =
.ft
f
-Z-
.
11.19. Show that F'(z) =
Io1[1n(llt)y-ldt
with Re(z) >
O.
11.20. Derive the identity
10
00
eX"
dx =
f[(a
+
1)la].
11.21. Consider the function f (z) =
(I
+
z)".
(a) Show that d"
fldznlz~o
=
I'(o
+1)1
I'(o
- n +
I),
and use it to derive the
relation
(
a) a!
f(a
+I)
where n
==
nl(a
- n)!
==
n!r(a
- n +I) .
(b) Show that for general complex numbers
a and b we can formally write
(a +b)a = t
(:)anb
a-
n.
n=O
(c) Show that if a is a positive integer m, the series in part (b) truncates at n = m.
11.22. Prove that the residue
of
I'(z)
at z =
-k
is rk =
(-I)klkL
Hint: Use
Equation (11.12)
11.23. Derive the following relation for z
= x +iy:
11.24. Using the definition of B(a, b), Equation (11.16), show that B(a, b) =
B(b, a).
11.25. Integrate Equation (11.21) by parts and derive Equation (11.11).
11.26. For positive integers
n, show that
f(~
-
n)r(~
+n) = (_1)n"..
11.27. Show that
(a) B(a, b) = B(a +I, b) +B(a, b + I).
(b) B(a, b +I) = C
~
b)
B(a, b).
(c) B(a,
b)B(a
+b, c) = B(b, c)B(a, b +c).
322
11.
COMPLEX
ANALYSIS:
ADVANCED
TOPICS
Imz
o
Rez
-it:
1-----
.....
----
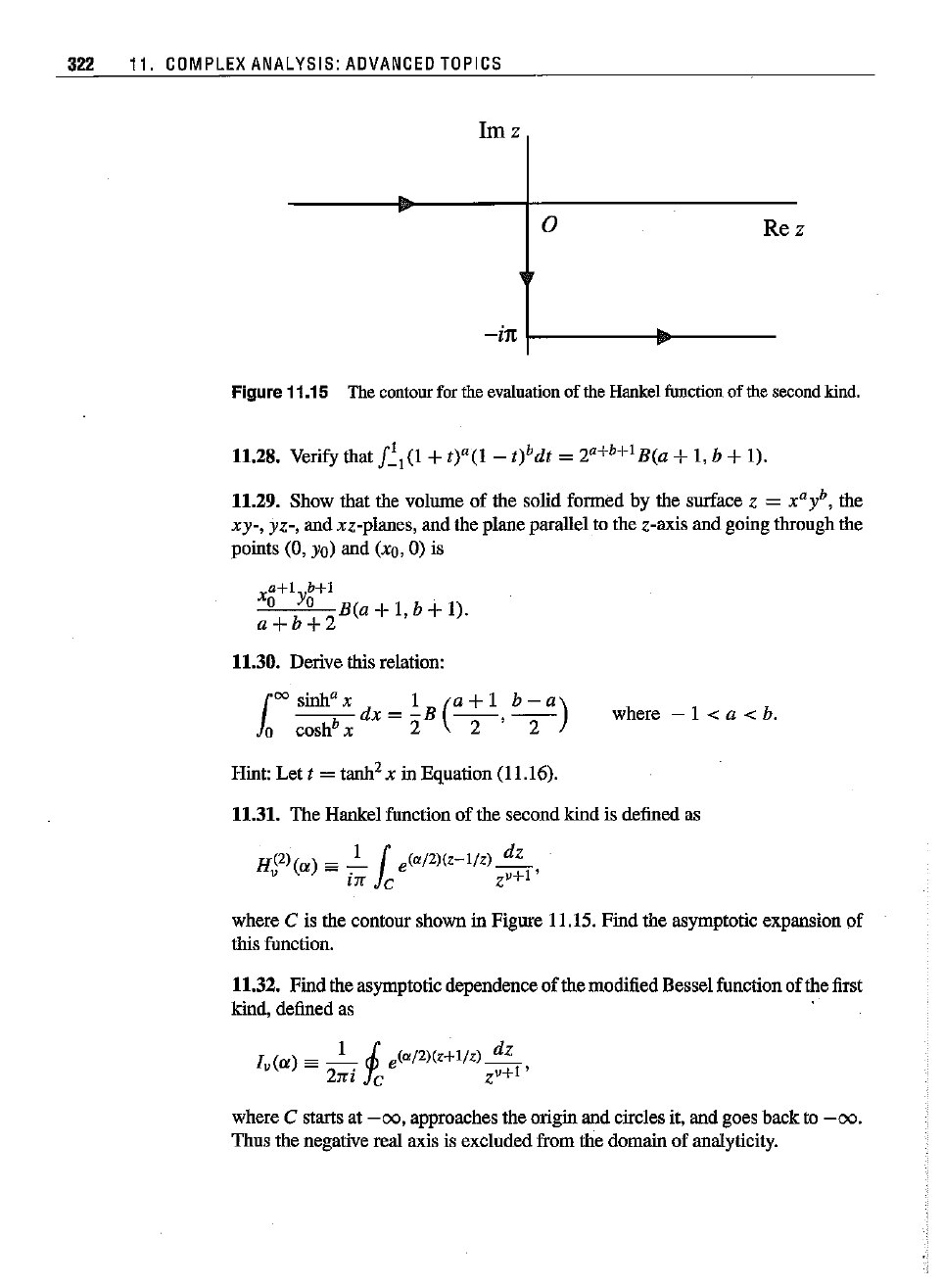
Figure 11.15 The contour for the evaluation of the Hankel function
of
the second kind.
11.28. Verify that
12
1
(1
+
t)a(l
-
t)bdt
= za+b+l
B(a
+1, b +1).
11.29. Show that the volume
of
the solid formed by the surface z = x
a
l,
the
xy-,
yz-, and xz-planes, and the plane parallel to the z-axis and going through the
points (0,
YO)
and (xo, 0) is
xa+1
b+l
o
Yo
B(a
+1, b +1).
a+b+Z
11.30. Derive this relation:
where - 1 < a < b.
Hint:
Let
t = tanh
2
x in Equation (11.16).
11.31. The Hankel function of the second kind is defined as
where C is the contour shown in Figure 11.15. Find the asymptotic expansion of
this function.
11.32. Find the asymptoticdependence
of
the modified Bessel function ofthe first
kind, defined as .
[v(ex) es
~
1.
e(a/2)«+I/<)
dz
,
2:rrz
Y
c
zv+l
where C starts at
-00,
approaches the origin and circles it, and goes backto
-00.
Thus the negative real axis is excluded from the domain of analyticity.
