Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations

Подождите немного. Документ загружается.

12.2

SEPARATION

OFTHEANGULAR PARTOFTHE

LAPLACIAN

333

equation as

la[a

]Ia

--L

(RY) +

r-(RY)

--(RY)

f(r)RY

r ar ar r ar

Dividing by

and multiplying by r

yields

I 2 r d

(dR)

r dR 2

--L

(Y)+--

+--+r

f(r)

=0,

Rdr

dr R dr

"-..-'

• I

-no +a

and

2dR

[

Ci]

'-+--+

f(r)--

R=O.

r dr r

(12.13)

(12.14)

We will concentrateon the angular part, Equation(12.13), leaving the radial partto

the general discussion of ODEs. The rest

this subsection will focus on showing

that Ll sa

Lx>

sa L

and

sa L

are independent of r.

Since Li is an operator, we can study its action on an arbitrary function

Thus,

L;j

-i€ijkX/'hf

-i€ijkXjaf/aXk.

We can express the Cartesian

Xj in terms of r, II, and tp, and use the chain rule to express

af/axk

in terms

spherical coordinates. This will give us Lif expressed in terms of r, II, and

rp.

will then emerge that r is absent in the final expression.

Let us start with x = r sin IIcos tp, Y = r sin IIsin tp, z = r cos II, and their

inverses,

r = (x

Z2)1/2,

cosll =

zfr,

tanrp =

Ylx,

and express the

Cartesian derivatives in terms of spherical coordinates using the chain rule. The

first such derivative is

all

arp

-=--+--+--.

ax ar ax all ax

arp

(12.15)

The derivative of one coordinate system with respect to the other can

be easily

calculated. For example,

arlax

x]r

= sinllcosrp, and differentiating both

sides of the equation cos II =

r, we obtain

. all

zarlax

-smll-

----

ax r

cos IIsin

cos

all cos IIcos

---'-

r ax r

Finally, differentiating both sides

tan

= YIx with respecttox yields

arp

Iax =

- sinrp/(r sinII). Using these expressions in Equation (12.15), we get

af.

cosllcosrpaf

sinrp

- =

smllcosrp-

+ -

---.

ax ar r all r sin II

arp

334 12.

SEPARATION

VARIABLES IN SPHERICAL

COOROINATES

exactly the same way, we obtain

af . . af cos esin I" af cos I" af

-=smesmqJ,,+

oe+-'-e'"

or r u r sm vI"

af af

sine

- =

cos()-

---.

az ar

Wecan now calculate

by lettingit act on an arbitraryfunction and expressing

all Cartesian coordinates and derivatives in terms

spherical coordinates. The

result is

. af . af .( . a a)

Lxf

-ly-

IZ-

= I

smqJ-

cote

cos

1"-

ay ae

aqJ

Cartesian

components

angular

momentum

operator

expressed

spherical

coordinates

= i (Sin

qJ~

cote

cos

qJ~)

aqJ

Analogous arguments yield

= i

(-cosqJ~

cote

SinqJ~),

aqJ

(12.16)

(12.17)

(12.18)

angular

momentum

squared

differential

operator

ine

and

is left as a problem for the reader to show that by adding the squares

the

components

the angular momentum operator, one obtains

2 I a

a) I a

L = -

sine

sme

- sin

aqJ2'

Substitution in Equation (12.12) yields the familiar expression for the Laplacian

in spherical coordinates.

12.3 Construction of Eigenvaluesof

Now that we have L

in terms of eand

1",

we could substitute in Equation (12.13),

separate the

eand I" dependence, and solve the corresponding ODEs. However,

there is a much more elegant way

solving this problem algebraically, because

Equation (12.13) is simply an eigenvalue equation for L

this section, we will

find the eigenvalues of L

•

The next section will evaluate the eigenvectors of L

Let us consider L

as an abstract operator and write (12.13) as

where

IY) is an abstract vector whose (e, qJ)thcomponent can be calculatedlater.

Since L

is a differential operator, it does not have a (finite-dimensional) matrix

12.3

CONSTRUCTION

EIGENVALUES

335

representation. Thus, the determinantal procedure for calculating eigenvalues and

eigenfunctions will not work here, and we have to find another way.

The equation above specifies an eigenvalue,

a, and an eigenvector, IY). There

may be more than one

IY) corresponding to the same a. Todistinguishamong these

so-calleddegenerate eigenvectors, we choosea second operator, say

E {L,}that

commntes with

This allows us to select a basis in which both L

and

are

diagonal,

or,

equivalently,

a basis whose

vectors

are

simultaneous

eigenvectors

of both L

and L3. This is possible by Theorem 4.4.15 and the fact that both L

and

are hermitian operators in the space

square-integrable functions. (The

proofis left as a problem.)

general, we wouldwant to continue adding operators

until we obtained a maximum set of commuting operators which could label the

eigenvectors.

this case, L

and

exhaust the set," Using the more common

subscripts

x, y, and z instead

1, 2, 3 and attaching labels to the eigenvectors,

we have

IY.,p) =

fJ 1Y.,p),

(12.19)

The hermiticity of L

and L

implies the reality

a and fJ. Next we need to

determine the possible values for a and fJ.

Define two new operators L+ sa

+iL

and L

- iL

is then easily

verified that

(12.20)

angular

momentum

raising

and

lowering

operalors

The first equation implies that L± are invariant operators when acting in the sub-

space corresponding to the eigenvalue a; that is, L±

1Y.,p)

are eigenvectors of L

with the same eigenvalue a:

2(L±

1Y.,p) = L±(L21Y.,p) =

aL±

1Y.,p).

The second equation in (12.20) yields

Lz(L+ IY.,p) =(LzL+)

1Y.,p)

=(L+L

+L+) IY.,p)

=L+L

1Y.,p)+L+ lYa,p) =fJL+

a,p) +L+

1Y.,p)

= (fJ +I)L+ IY.,p) .

This indicates that L+

1Y.,p)

has one more unit of the L

eigenvalue than

1Y.,p)

does. In other words, L+ raises the eigenvalue of L

by one unit. That is why L+

is called a

raising

operator.

Similarly, L is called a lowering

operator

because

Lz(L

1Y.,p)

= (fJ -

I)L

a,p).

Wecan

summarize

theabovediscussion as

6Wecouldjustas well havechosenL

andany

other

component

asourmaximalset.

However,

and

is the

universally

accepted choice.

336 12.

SEPARATION

VARIABLES

SPHERICAL

COOROINATES

where C± are constants to be determined by a suitable normalization.

There are restrictions on (and relations between) 01 and p.First note that as L

is a sum

squares of hermitian operators, it must be a positive operator; that is,

(al L

1a)

::::

0 for all ]c). In particular,

0::;

(Ya,~1

L2IYa,~)

= 01

(Ya,~1

Ya,~)

0IIIYa,~1I2.

Therefore, 01 ::::

Next, one can readily show that

L+L

+L; - L

LL+

+L; +L

(12.21)

Sandwiching both sides of the first equality between I

Ya,~)

and

(Ya,~

Iyields

(Ya,~1

L2IYa,~)

(Ya,~1

L+L

IYa,~)

(Ya,~1

lYa,~)

(Ya,~1

lYa,~),

with an analogous expression involving

LL+.

Using the

fact

that L+ =

(L)t,

we get

0IIIYa,~1I2

(Ya,~1

L+L

IYa,~)

p2I1Ya,~1I2

PIIYa,~1I2

(Ya,~1

LL+

IYa,~)

p2I1Ya,~1I2

PIIYa,~1I2

= liLT

IYa.~)

p2I1Ya,~

PllYa,~1I2

(12.22)

Becauseof the positivity

ofnonns,

this yields 01 :::: p2 - P and 01 :::: p2 +p. Adding

these two inequalities gives

201 :::: 2p2

-v'{i::;

p ::; v'{i.

follows that the

values of pare bounded. That is, there exist a maximum p,denoted by

P+,

and

a minimum

denoted by

p_,

beyond which there are no more values of p. This

can happen only

because if L±

lYa,~±)

are not zero, then they must have values of p corresponding

P±

± 1, which are not allowed.

Using

P+

for pin Equation (12.22) yields

(01-

P+)llYa,~+1I2

= O.

By definition

lYa,~+)

oft

0 (otherwise

P+

- 1 wonld be the maximum). Thus, we

obtain

01 =

P+

An analogousprocedureusing

for p yields 01 = P:-

p_.

We solve these two equations for

P+

and

p_:

P+

!(-I

±"'1

+4a),

=!(I

"'I

+4a).

Since

P+

::::

and

"'1

+401 :::: I, we must choose

P+

=!(

-I

+"'1 +

401)

=-p_.

forkEN,

eigenvalues

ofL'

and

given

12.3

CONSTRUCTION

EIGENVALUES

337

Startingwith 1

Ya.~+),

we can apply L_ to itrepeatedly. In eachstep we decrease

the value

by one unit. There mustbe a limitto the number of vectors obtained

in thisway,because

hasa

minimum.

Therefore,

there

mustexist a nonnegative

integer k such that

(L)k+1IYa,~+)

L(L~

lYa,~+))

Thus,

lYa,~+)

must be proportioual to

lYa,~_).

In particular, since

IYa,~+)

has a

value equal to

fJ+

- k, we have fJ- =

fJ+

- k. Now, using

fJ-

= -fJ+

(derived above) yields the important result

k .

fJ+=Z=J

or a = j

+1), since a = fJt+

fJ+.

This result is important enough to be stated

as a

theorem.

12.3.1.

Theorem.

Theeigenvectors

of~,

denotedby 1Yjm),satisfytheeigenvalue

relations

Yjm)

j(j

+1) IYjm) ,

IYjm) =

m IYjm) ,

where j is a positive integer or half-integer, and m can take a value in the set

I-j,

-j

+1,

...

-1,

of2j

+1 numbers.

Let us briefly considerthe normalization of the eigenvectors. Wealready know

that the

IYjm), being eigenvectors

the hermitian operators L

and L

are orthog-

onal. We also demand that they be of unit norm; that is,

(12.23)

(12.24)

This will determine the constants C±, introduced earlier. Let ns consider C+ first,

which is defined by

L+ IYjm) = C+ IYj,m+l). The hermitian conjngate of this

equation is

(Yjml L = C':' (Yj,m+ll. We contract these two eqnations to get

(Yjml

LL+

jm)

IC+1

(Yj,m+ll Yj,m+l). Then we use the second relation

in Equation

(12.21), Theorem 12.3.1, and (12.23) to obtain

+1) - m(m +1) =1C+1

1C+1=

-/"j-;-(j:---+:---I:7)---m:---(:---m-+:---I'"'").

Adopting the convention that the argument (phase) of the complex number C+ is

zero (and therefore that

C+ is real), we get

C+ =

.jj(j

+1)

-m(m

+1)

Similarly,

C-

+1) m(m 1). Thus, we get

L+ IYjm) =

,jj(j

+1) -

m(m

+1) IYj,m+l) ,

L IYjm)

=,j

j(j

+1) -

m(m

- 1)

IYj,m-l).

338

12.

SEPARATION

VARIABLES

SPHERICAL

COOROINATES

12.3.2. Example. Letusfindanexpressionfor IYl

byrepeatedly applying

L-

to IYu).

TheactionforL_ is completely

described

Equation

(12.24).Forthe

first

power

of L_,

obtain

L-lYu)

= ,//(/+

-/(/-1)

IYI,I-I}

J2l1Y1,l-1).

apply

L_ once

(L-)2IYU)

J2lL-1Y1,1-l}

J2l,//(l

(/-

1)(/-

2) IYI,I-2}

J2l,/2(21

- I)

1Y1,1-2}

= ,/2(21)(2/ - I) 1Y1,1-2)'

Applying

L-

a thirdtimeyields

(L-)3

IYU)

,/2(2/)(2/-

1)L-IYI,l-2}

,/2(21)(2/-

1),/6(/-

1Y1,1-3)

= ,/3!(21)(21 - 1)(21 - 2)

IYI,H}.

The

pattern

suggeststhefollowing

formula

fora generalpowerk:

lYu) =

,/k!(2/)(21-I)

...

(2/-

k + I) 1Y1,I-k},

lYu} = ,/k!(21)!j(21 k)!

1YI,I-k).lfwe

set

k =m andsolvefor IYI,m)' weget

}

+m)!

l-mIY)

IYl,m

_m)!(21)!

iu-

III

The discussioninthis sectionis the standardtreatment

angularmomentumin

quantum mechanics.

In the context

quantum mechanics, Theorem 12.3.1 states

the far-reaching physicalresult thatparticles

can

have integer

half-integerspin.

Suchaconclusionistiedtothe

rotation

group

three

dimensions, which,intum, is

an exaruple

aLie group,or acontiuuousgroup

transformations. We shall come

backto a study

groups later.

is worthnotiug thatit was the study

differential

equations that led the Norwegian mathematician Sophus Lie to the investigation

their symmetries and the development

the beautiful branch

mathematics

and theoretical physics that bears his narue. Thus, the existence

a conuection

betweengroup theory (rotation, angularmomentum) and the differential equation

we are trying to solve should not come as a surprise.

12.4 Eigenvectors

: Spherical Harmonics

The treatment in the preceding section took place in an abstract vector space.

Let

us go

back

tu the fuuction space and represent the operators and vectors in terms

0 and

<p.

First, let us consider L

in the form

a differential operator, as given in

Equation (12.17).

The

eigenvalue equation for L, becomes

12.4

EIGENVECTORS

SPHERICAL

HARMONICS

339

We write Yjm(O,

<p)

= Pjm(O)Qjm(<P) and substitute in the above equation to

obtain the ODE for

<p,

dQjm/d<p

ImQjm,

which has a solution of the form

Qjm(<P) =

Cjmeim~,

where

Cjm

is a constant. Absorbing this constant into Pjm,

we can

write

Yjm(O,

<p)

Pjm(O)eim~.

In classical physics the value of functions must be the same at

as at

This condition restricts the values of m to integers. In quantum mechanics, on the

other hand, it is the absolute values of functions that are physically measurable

quantities, and therefore

m can also be a half-integer.

12.4.1. Box.

From

now on, we

shall

assume

that

m isan integer

and

denote

the eigenvectors

by Ylm(0,

<p),

which

1Is a nonnegative integer.

Our task is to find an analytic expression for Ylm(O, <pl.We need differential

expressions for L±. These can easily be obtained from the expressions for

and

given in Equations (12.16) and (12.17). (The straightforward manipulations are

left as a problem.) We thus have

L± =

e±i~

(±~

+ i

cotO~)

. (12.25)

a<p

Since 1is the highest value

ofm,

when L+ acts on Yll(O,

<p)

Pll(O)eil~

the result

must be zero. This leads to the differential equation

(:0

+ I cot 0

aa<p)

[Pll(O)eil~]

(:0

-I

cot 0)Pll(O) =O.

The solution to this differential equation is readily found to be

Pll

(IJ)

= CI(sin0)1.

The constant is subscripted because each Pll may lead to a different constant of

integration. We can now write Yll(O,

<p)

CI(sinO)Ieil~.

With Yll(O,

<p)

at our disposal, we can obtain any Ylm(O,

<p)

by repeated ap-

plication of

In principle, the result

Example 12.3.2 gives all the (abstract)

eigenvectors. In practice, however, it is helpful to have a closed form (in terms

of derivatives) for just the

0 part of Ylm(O, <pl. So, let us apply

as given in

Equation (12.25) to

Yll(O,

<p):

. ( a a)

LYli

e-'~

+ I

cotO-

[Pll(O)e'~]

a<p

e-i~

cotO(il)]

[Pll(O)eil~]

(_I)ei(l-l)~

(:0

+lcotO)

Pll(O).

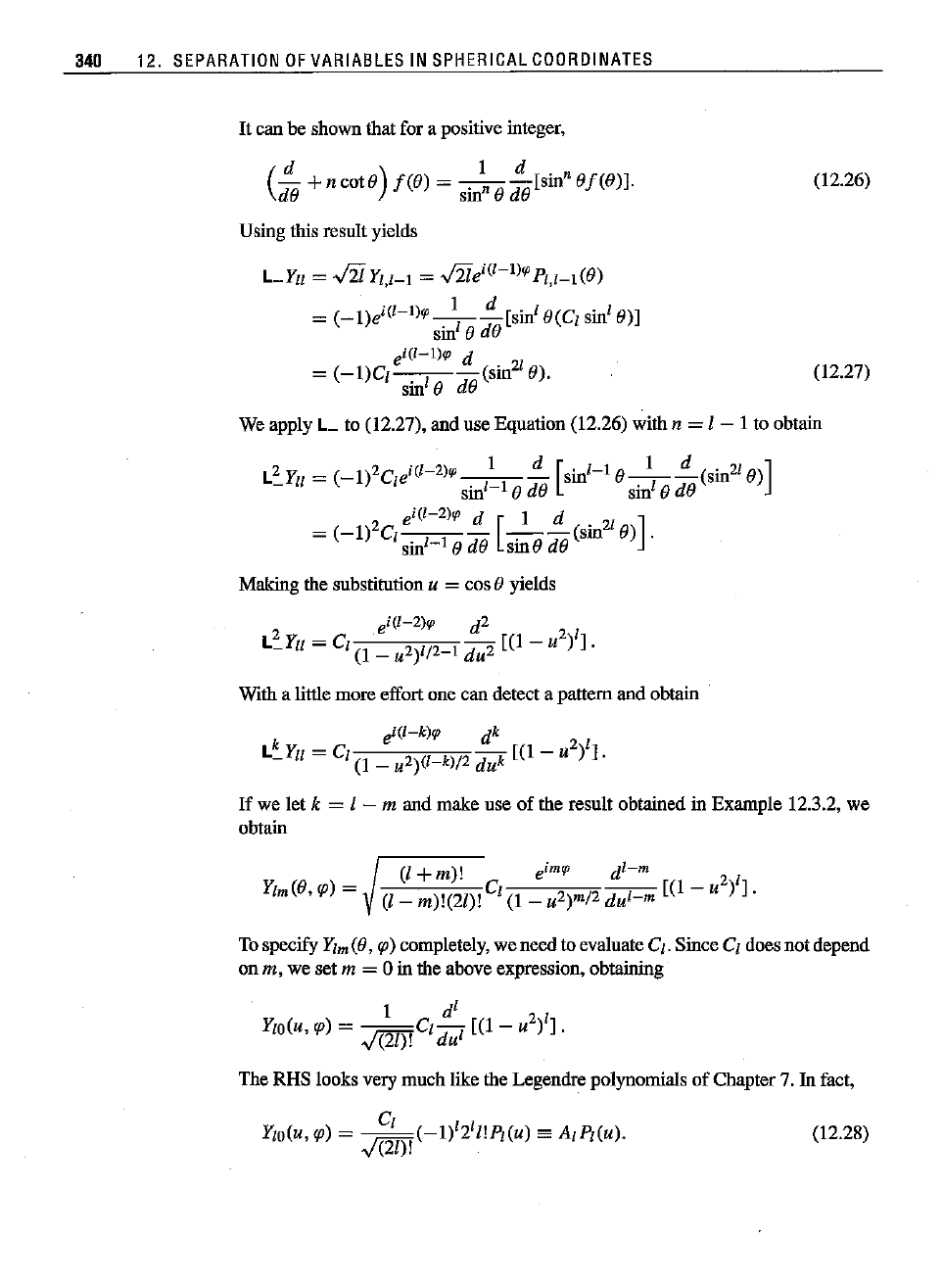
340 12.

SEPARATION

VARIABLES

IN SPHERICALCOORDINATES

can be shown that for a positive integer,

(

d )

I d

+ncotO

f(O)

= sinnOdO[sm Of(O)].

Using this result yields

(12.26)

(12.27)

LYIl

v'2i

YI.I-l

v'2iei(l-ll~

PI,

1-1

(0)

(_I)ei(I-ll~_I_~[sini

O(CI sin

0)]

siniO dO

ei(I-l)~

(-I)CI---(sin

0).

sinlO dO

We apply L to (12.27), and use Equation (12.26) with n = I - I to obtain

With a little more effort one can detect a pattern and obtain

i (l

)

k (

2)1

L_Yn = CI (1 _ u

2)(l-kl(2

[ I - u ] .

we let k = I - m and make use of the result obtained in Example 12.3.2, we

obtain

YIm(O,

rp)

+m)!

eim~

--,-'---'-c-=,...,C

[(I

_ u

)I]

(1-

m)!(21)! I

_ u

2)m(2

du'

m .

Tospecify

Ylm(O,

rp)

completely, we need to evaluate CI. Since CI does not depend

m, we set m = 0 in the above expression, obtaining

I d

2 I

YlO(U,

rp)

IMmCIdl

[(1 - u )

(21)!

The RHS looks very much like the Legendre polynomials

Chapter 7. In fact,

YlO(U,

rp)

~(-1)1211!PI(U)

AIPI(U).

v (21)!

(12.28)

(12.30)

12.4

EIGENVECTORS

SPHERICAL

HARMONICS

341

Therefore, the normalization

YIO

and the Legendre polynomials Pi determines

Ct.

We now use Equation (6.9) to obtain the integral form

the orthonormality

relation

forYl

(12.29)

which in terms of

u = cos ebecomes

dip

Yt;m'(U'

<P)Ytm(U,

<p)du

811'8

-t

Problem 12.15showsthatnsing(12.29) one gets At = .)(21 +

l)j(4n).

Therefore,

Equation (12.28) yields not only the value

Ci, but also the useful relation

YIO(U,

'1')

--Pt(u).

spherical

harmonics

Substituting the value of Ct thus obtained, we finally get

(12.31)

where

u = cos

These functions, the eigenfunctions of L

and L

are called

spherical harmonics. They occur frequently in those physical applications for

which the Laplacian is expressed in terms

spherical coordinates.

One can immediately read off the

epart of the spherical harmonics:

t('ii+ll

Ptm(u) =

(-1)

tl!

However, this is not the version used in the literature. For historical reasons the

associated

Legendre

associated

Legendre

functions Pt(u) are used. These are defined by

functions

m m

(I+m)!

(u) =

(-1)

(1-

m)!V

2i+1

Ptm

(u)

(

2)-m/2

= (_I)t+m

- u

[(1-

u2iJ.

(1-

m)!

»n

du'

Thus,

Ytm(e,

'1')

(_1)'"

[21

i::

:;:t

pt"'<cose)ei"'~.

(12.33)

(12.34)

342 12.

SEPARATION

VARIABLES

SPHERICAL

COOROINATES

We generated the spherical harmonics starting with Yl!(0,

<p)

and applying the

lowering operator

could

have started

with

YI,-I(O,

<p)

instead, and applied

the raisingoperator

L+.

The

latterprocedureis identicalto the former; nevertheless,

we outlineit below because

someimportantrelations thatemergealongthe way.

We first note that

(I +

m)!

LI- ", IY )

IYI,-",)

= (I _ m)!(21)! +

1,-1·

(12.35)

(This can be obtained following the steps

Example 12.3.2,) Next, we use

L IYI,-I) = 0 in differential form to obtain

(:0

-I

cot

0) PI,-I(O) = 0,

which has the same form as the differential equation for Pl!. Thus, the solution is

PI,_I(O) = Cf(sinO)I, and

YI,_I(O,

<p)

PI,_I(O)e-il~

C;(sinO)le-il~.

Applying L+ repeatedly yields

k I

(-lle-i(l-k)~

2 I

L+YI,_I(U,

<p)

= C

_ u2)(l k)j2 du

[(1 - U )

where U = cos

Substituting k = 1- m and using Equation (12.35) gives

YI,-",(U,

<p)

The constant Cf can be determined as before.

In fact, for m = 0 we get exactly

the same result as before, so we expect Cf to be identical to

CI. Thus,

Comparison with Equation (12.32) yields

YI,_",(O,

<p)

(-I)"'YI~"'(O,

<p),

(12.36)

(12.37)

andusingthedefinition Pic.s.Ie',

<p)

PI,_",(O)e-i"'~

and the first part

Equation

(12.33), we obtain

P-"'(O)

(-1)'"

(1-

m)!

pm(O).

I (l +

m)!