Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


13.3
GENERAL
PROPERTIES
OF
SOLDES
353
(13.10)
normal
form
ofa
SOLDE
singular
points
ofa
SOLDE
Dividing by P2(X) and writing P for
Pl/
P2, q for
pol
P2, and r for
P3/
P2reduces
this to the
normal
form
d
2y
dy
-2
+
P(x)-d
+
q(x)y
= rex).
dx
x
Equation (13.10) is equivalent to (13.9) if P2(X)
i'
O.
The
points at which P2(X)
vanishes are called the
singnlar
points
of
the differential equation.
There is a crucial difference between the singular points
of
linear differential
equationsand those
of
nonlineardifferentialequations. For a nonlineardifferential
equationsuchas
(x
2_y)y'
= x
2+y2,
thecnrve
y = x
2
is the collection
of
singular
points. This makes it impossible to construct solutions
y = f (x) that are defined
on an interval
I = [a, b]
of
the x-axis because for any x E I, there is a y for
which the differential equation is undefined.
Linear differential equations do not
have this problem, because the coefficients
of
the derivatives are functions
of
x
only. Therefore, all the singular "curves" are vertical. Thus, we have the following
definition.
(13.11)where
L[y]=P3,
13.3.1. Definition. The normalform
of
a
SOWE,
Equation (13.10), is regularon
an interval [a, b]
of
the x-axis if
p(x),
q(x),
and
rex)
are continuous on [a, b].
A solution
of
a normal
SOWE
is a twice-differentiable function y =
f(x)
that
satisfies the
SOLVE
at every point
of[a,
b].
It
is clear that any function that satisfies Equation (13.1O)--{)r Equation
(13.9)-must
necessarily be twice differentiable, and that is all that is demanded
of
the solutions. Any higher-orderdifferentiabilityrequirement
may
be too restric-
tive, as was pointed out in Example 13.1.1. Most solutions to a normal SOLDE,
however, automatically have derivatives
of
orderhigher than two.
We write Equation (13.9) in the operatorform as
d
2
d
L sa P2
dx
2
+
PI
dx
+
PO·
regular
SOLDE
It
is clear that L is a linear operator because d/
dx
is linear, as are all powers
of
it. Thus, for constants a and {J, L[aYI +
{JY2]
= aL[yJl +
{JL[Y2].
In particular,
if
Yl and Y2 are two solutions
of
Equation (13.11), then
L[YI
-
Y2]
=
O.
That
is, the difference between any two solutions
of
a
SOLDE
is a solution
of
the
homogeneous
equation
obtained by setting P3 = 0.
2
An immediate consequence
of
the linearity
of
L is the following:
13.3.2.
Lemma.
lj'L[u] =
rex),
L[v] = sex), a
and
{J
are constants, and w =
au
+{Jy, then
L[w]
=
ar(x)
+{Js(x).
The
proof
of
this
lemma
is trivial, but the resultdescribes the fundamentalprop-
erty
of
linear operators: When r = s = 0, that is, in dealing with homogeneous
superposition
principle
2Thisconclusion is, of
course,
not
limited
tothe
SOLDE;
itholdsforall linear DEs.

354 13.
SECOND-ORDER
LINEAR
DIFFERENTIAL
EQUATIONS
equations, the lennna says that any linear combination of solutious
of
the homo-
geneous SOLDE (HSOLDE) is also a solution. This is called the superposition
principle.
Based on physical intuition, we expect to be able to predict the behavior of
a physical system
if
we know the differential equation obeyed by that system,
and, equally importantly, the initial data. A prediction is not a prediction unless it
is unique.' This expectation for linear equations is bome out in the language of
mathematics in the form of an existence theorem and a uniqueness theorem. We
consider the latter next. But first, we need a lennna.
13.3.3.
Lemma.
Theonly solution
g(x)
of
thehomogeneous equation
s"
+
py'
+
qy =0 definedon the interval [a, b] that satisfies
g(a)
= 0 =
g'(a)
is the
trivial
solution g =
O.
Proof
Introduce the nounegative function
u(x)
es [g(x)]2 +[g'(x)]2 and differ-
entiate it to get
u'(x)
=2g'g +
2g'
g"
=
2g'(g
+
g")
=
2g'(g
-
pg'
-
qg)
=
_2p(g')2
+ 2(1 -
q)gg'.
Since (g ± g')2 2:0, it follows that 21gg'I ::: g2 +
e".
Thns,
2(1 -
q)gg'
::: 21(1 -
q)gg'l
= 21(1 - q)1 Igg'l
s
1(1
-
q)l(g2
+ g'2)
.s
(I
+ Iql)(g2 + g'2),
and therefore,
u'(x):::
lu'(x)1 =
1-
2pg,2 +
2(1-
q)gg'l
s 21plg,2 +
(I
+ Iql)(g2 + gl2)
= [I + Iq(x)l]g2 + [I + Iq(x)1
+2Ip(x)l]gl2.
Now let K = I
+max[lq(x)1
+2Ip(x)J],
where the maximum is taken over [a, b].
Then we obtain
u'(x):::
K(g2
+g'2) =
Ku(x)
Vx E [a, b].
Using the resnlt of Problem 13.1 yields
u(x)
::: u(a)eK(x-a) for all x E [a, b].
This equation, plus
u(a)
= 0, as well as the fact that
u(x)
2:0 imply that
u(x)
=
g2(x) +gl2(x) =
O.
It
follows that
g(x)
= 0 =
g'(x)
for all x E [a, b]. D
uniqueness
of 13.3.4. Theorem. (Uniqueness theorem)
If
p and q arecontinuous on [a, b], then
solutions
fa
SOLDE
3Physical
intuition
also tells us that
if
the initial conditions are
changed
by an infinitesimal
amount,
then the solutions
will be changedinfinitesimally. Thus,the solutionsof linear
differential
equations are saidto be continuous
functions
of the
initialconditions. Nonlinear
differential
equations
can have completelydifferent solutionsfor two initialconditions
that
are
infinitesimally
close. Sinceinitialconditions
cannot
be specifiedwith
mathematical
precision in
practice,
nonlinear
differential
equations
leadto
unpredictable
solutions, orchaos.This
subject
hasreceivedmuch
attention
inrecent
years.
Foran
elementary
discussionof chaossee [Hass99,
Chapter
15].

13.4 THEWRONSKIAN 355
atmostone solution y = f (x)
of
Equation (13.10)cansatisfytheinitial conditions
f(a)
= Ci and
I'(a)
=C2, where Ci and C2 are arbitrary constants.
Proof Let
fl
and
12
be two solutions satisfying the given initial conditions. Then
their difference, g
es
fl
-
12,
satisfies the bomogeneous equation [witb rex) = 0].
The initial condition that
g(x) satisfies is clearly g(a) =a=g'la). By Lemma
13.3.3,
g = aor
!I
=
h.
0
Theorem 13.3.4 can be applied to any
homogeneous SOLDE to find the latter's
most general solution. In particular, let
!I
(x)
and
12
(x) be any two solutions of
y" +
p(x)y'
+
q(x)y
= 0
(13.12)
defined on the interval
[a, b]. Assnme that the two vectors VI =
(fl(a),
fila»~
and V2 =
(h(a),
f~(a»
in
IR
2
are linearly independent," Let g(x) be another
solution. The vector
(g(a), g'(a)) can be written as a linear combination of VI and
V2, giving the two equations
g(a) =
cdl(a)
+c2h(a),
g'(a) = Cif{(a)
+c2f~(a).
Now consider the function
u(x)
ea g(x) -
cdl(x)
-
c2h(x),
which satisfies
Equation (13.12) and the initial conditions
ural =u'(a) =
O.
By Lemma 13.3.3,
we must have
u(x) = 0 or
g(x)
= Ci!l(X) +
c2h(x).
We have proved the
following:
13.3.5.
Theorem.
Let
fl
and
12
be two solutions
of
the
HSOWE
v"
+
py'
+qy = 0,
where p and q are continuousfunctions definedon the interval [a,b].
If
(fl(a),
flea»~
and
(h(a),
f~(a))
are linearly independent vectors in
IR
2,
then every solution g(x)
of
this
HSOWE
is equal to some linear combination g(x) =
CI
!I
(x)
+c2h(x)
of
fl
and
12
with
constantcoefficients Cl andC2.
13.4 The Wronskian
The two solntions
fl(x)
and
hex)
in Theorem 13.3.5 have the property that any
other solution g
(x) can be expressed as a linear combination of them. We call
basis
of
solutions
fl
and
12
a
basis
of solutions of the HSOLDE. To form a basis
of
solutions,
!I
4If theyarenot,thenone mustchoosea
different
initial pointforthe
interval.

356 13.
SECOND-ORDER
LINEAR
DIFFERENTIAL
EQUATIONS
and h must be linearly independent. The linear dependence or independence of
a number
of
functions
If;
1i'=1
: [a, b] --> lit is a concept that must hold for all
x E [a, b]. Thus,
if
(a;}i'~1
E lit can be found such that
for some
XQ E [a, b], it does not mean that the
j's
are linearly dependent. Linear
dependence requires that the equality holdfor all
x E [a, b].
In
fact, we mustwrite
aIfI
+
a2h
+...+
anfn
= 0,
where 0 is the zero function.
Wronskian
defined
13.4.1. Definition. The Wronskian
of
any two differentiable functions
II
(x) and
h(x)
is
(
fJ (X)
W(fl,
h:
x)
=
lI(x)f~(x)
-
h(x)f{(x)
= det
h(x)
f{(X»)
.
f~(x)
13.4.2. Proposition. The Wronskian
of
any two solutions
of
Equation (13.12) sat-
isfies
where c is any number in the interval [a, b].
Proof.
Differentiating both sides of the definition
of
Wronskian and substituting
from Equation (13.12) yields a FOLDE for
W(fl,
h:
x),
which
can
be easily
solved. The details are left as a problem.
D
An important consequence of Proposition 13.4.2 is that the Wronskian of any
two solutions
of
Equation (13.12) does not change sign in [a, b].
In
particular, if
the Wronskian vanishes at one pointin
[a, b], it vanishes at all points in [a, b].
The real importance of the Wronskian is contained
in
the following theorem.
13.4.3.
Theorem.
Two differentiable functions
fl
and
h,
which are nonzero in
the interval
[a',b], are linearly dependent if
and
only iftheir Wronskian vanishes.
Proof.
If
fl
and h are linearly dependent, then one is a multiple of the other, and
the Wronskian is readily seen to vanish. Conversely, assume that the Wronskian
is
zero.
Then
lI(x)f~(x)
-
h(x)f{(x)
= 0 ~
IIdh
=
hdfl
~
h = elI
and the two functions are linearly dependent.
D

ifx?;O
if
x::::
0
13.4
THE
WRONSKIAN
357
Josef
Hoene de Wronski (1778-1853) was hom Josef Hoene, hut he adopted the name
Wronski
around
1810justafterhe married, Hehadmovedto
France
andbecomea French
citizenin 1800andmovedto Parisin 1810,thesameyearhe publishedhis firstmemoiron
the
foundations
of
mathematics,
whichreceivedless
than
favorable
reviews
from
Lacroix
and
Lagrange.
His
other
interests
included
thedesignof
caterpillar
vehiclestocompetewith
the
railways.
However,
theywerenever
manufactured.
Wronski
was
interested
mainlyin
applying
philosophyto
mathematics,
the
philosophy
taking
precedence
over
rigorous
mathematical
proofs.
Hecriticised
Lagrange's
use of infinite
seriesand
introduced
hisownideasforseriesexpansions of a
function.
Thecoefficientsin this seriesaredeterminants now
known
as Wronskians [so
named
by
Thomas
Muir
(1844-
1934), a GlasgowHigh School science
master
who became
an
authority
on determinants by devoting most of his life to
writing
afive-volume
treatise
onthe
history
of
determinants].
For
many
years
Wronski's
workwasdismissedas
rubbish.
However,
a closer
examination
of the workin more recent
timesshowsthat
although
someis wrongandhe hasan
incredibly
high
opinion
of himself
andhisideas,
there
arealsosome
mathematical
insights of
great
depthand
brilliance
hidden
within
the
papers.
13.4.4.
Example.
Let
I:
(x) = x and
h(x)
= Ixlfor x E
[-1,1].
These two functions
are
linearly
independent
inthegiven
interval,
because
al
x +a21xI= 0for all x
if
andonly
if ''1 =
ez
=O.The Wronskian, on the other hand, vanishes for all x E
[-1,
+1]:
dlxl dx dlxl
W(ft,
fz; x) =
x-
-Ixl-=
x-
-Ixl
dx dx dx
d
{x
ifx>O
{x
= x dx
-x
if x
~
0 -
-x
{
X -
x =0
if
x > 0
=
-x
-
(-x)
= 0 if x < O.
Thus,
itis possiblefortwo
functions
to havea
vanishing
Wronskian
without
being
linearly
dependent.
However,
as we showedin the proof of the
theorem
above,if the
functions
are
differentiable
in
their
interval
of
definition,
thenthey
are
linearly
dependent
if
their
Wronskian
vanishes.
II
13.4.5. Example. The
Wronskian
canbegeneralized to n
functions.
The
Wronskian
of
the functions fJ,
h.
... ,[n is
(
fJ
(x)
h(x)
W(ft,fz,
...
,fn:
x) = det :
fn(x)
f{(x)
f5.(x)
f/'(x)
fi"_l)(X»)
f}"-l)
(x)
fJn-l)
(x)

358 13.
SECOND-ORDER
LINEAR
DIFFERENTIAL
EQUATIONS
If
the functions are linearlydependent,then
W(ft,!2,
...
, in; x) =
O.
For
instance,
itisclear
that
eX,
e-
x,
andsinhx are
linearly
dependent.
Thus,
we
expect
(
e" e"
ex)
W(e
X
,
e-
x,
sinh x; x) = det
e-
x
_e-
x
e-
x
sinhx coshx sinhx
to
vanish,
asis easilyseen(the
first
and
last
columns
arethe
same).
13.4.1 A Second Solution to the HSOLDE
If
we know one solution to Equation (13.12), say
ft,
then by differentiating both
sides
of
h(x)fi(x)
-
h(x)f{(x)
=
W(x)
=
W(e)e-
J:
p(t)dt,
dividing the result by f
1
2
,
and noting that the
LHS
will be the derivative
of
hi
h,
we can solve for
12
in
tenus
of
ft.
The
result is
hex)
= fleX)
{C
+K 1
X
---i-
exp [-1'
p(t)dt]
dS}
,
a f
l
(S)
c
(13.13)
ke
kx
)
-ke-
kx
=
-2k,
where K
'"
W(c) is another arbitrary (nonzero) constant; we do not have to know
W
(x)
(this would require knowledge
of
12,
which we are trying to calculate!)
to obtain
Wee). In fact, the reader is urged to check directly that
hex)
satisfies
the DE
of
(13.12) for arbitrary C and
K.
Whenever
possible-and
convenient-
it is customary to set C = 0, because its presence simply gives a term that is
proportional
to the known solution
ft
(x).
13.4.6. Example. (a)A solutionto the SOLDE y" - k
2
y = 0 is e
kx.
To finda second
solution, welet C = 0 and
K = I 10Equation(13.13).Since
p(x)
= 0,we have
(
1
x ds ) I
e-
2ka
!2(x)=e
kx
0+
a e
2k
'
=-2ke-kx+~t!X,
which,
ignoring
the
second
term
(whichis
proportional
tothe
first
solution),
leads
directly
tothechoiceof
e-
kx
asasecond
solution.
(h) Thedifferentialequation
y"+k
2y
= ohassinkx asasolution. WithC = O,a = rr/(2k),
andK
= I, weget
!2(x)
=slokx
(o+l
x
.~
)
=-slokxcotksl;/2k
= - coskx .
1r/2ksm ks
(c)For the solotions in part (a),
(
e
kx
W(x) = det
e-
kx
andfor thoseinpart(h),
W(x) = det (SlokX
coskx
kcoskx
)
=-k
-ksiokx
.

13.4
THE
WRONSKIAN
359
Both
Wronskians
are
constant.
In
general,
the
Wronskian
of anytwo
linearly
independent
solutions of y" +q(x) y =0 is
constant.
II
Most
specialfunctions usedin mathematicalphysics are solutions
of
SOLDEs.
The behavior
of
these functions at certain special points is determined by the
physics
of
the particular problem.
In
most
situations physicalexpectation leads to
a preferencefor one particularsolution over the other. For example, although there
are two linearly independent solutions to the Legendre DE
~
[(I
- x
2
)
d
Y]
+
n(n
+
I)y
= 0,
dx
dx
the solution thatis
most
frequently encounteredis the Legendrepolynomial P
n
(x)
discussedin Chapter7. The othersolntioncan be obtainedby solvingthe Legendre
equation or by using Equation
(13.13), as done in the following example.
13.4.7.
Example.
TheLegendreequationcanbereexpressedas
d
2y
2x dy
n(n
+ I)
dx2 - I _ x
2
dx + I _ x2 Y =
O.
Thisis an
HSOWE
with
p(x)
=
-~2
and
q(x)
=
n(n
+
I)
I-x
I-x
2
One solutionof thisHSOLDEis the well-knownLegendrepolynomial P
n
(x).
Usingthis
asourinputandemploying
Equation
(13.13), we can
generate
another
set
of
solutions.
Let
Qn(x)
stand for the linearly independent''partner'' of Pn(x). Then, setting C =
0=
c in Equation(13.13)yields
Qn(x) =
KPn(x)
1
x
+exp
[['
~
-l
d.
" P
n
(s) 1
0
I -
t
=
KPn(x)lx
+
[~]
d.
= A
nP
n(x)l
x
~.
2 '
a
P
n
(s}
1-.
"
(I
-.
)P
n
(.)
where
Anis an
arbitrary
constant
determinedby
standardization,
anda is an
arbitrary
point
inthe
interval
[-1,
+1].Forinstance,forn = 0, we have Po = 1, andwe obtain
for Ixl< 1.
for Ixl< 1.
1
x
d.
[I
II+xl
I 1
1
+"1]
QO(x) = Ao
--
= Ao
-In
--
-
-In
--
.
"1-.
2
2
I-x
2
1-"
The standardform of Qo(x) is obtainedby settingAo = I
and"
= 0:
I
II
+x
I
Qo(x) =
-In
--
2
I-x
Similarly, since Pt
(x)
= x,
1
x
d.
II
+x
I
Ql(X)=AlX
2 2
=Ax+Bxln
--
+C
" s (I
-.
) I - x
Here
standardization
is A = 0, B = !'andC =
-1.
Thus,
I
II
+x
I
Ql(X) =
-xln
--
-1.
2
I-x
III

360 13.
SECOND-ORDER
LINEAR
DIFFERENTIAL
EQUATIONS
13.4.2 The General Solution to an ISOLDE
Inhomogeneous SOLDEs (ISOLDEs) can be most elegantly discussed iu terms
of
Green's functions, the subject of Chapter 20, which automatically iucorporate the
boundary conditions. However, the most general solution of an ISOLDE, with no
boundary specification, can be discussed at this poiut.
Let
g(x)
be a particular solution
of
L[y]
=
y"
+
py'
+
qy
=
r(x)
(13.14)
and let
h(x)
be any other solution of this equation. Then
h(x)
-
g(x)
satisfies
Equation (13.12) and can be written as a liuear combiuation
of
a basis
of
solutions
fl
(x)
and h
(x),
leading to the followiug equation:
h(x)
=
CJfl(x)
+
ezh(x)
+
g(x).
(13.15)
Thus,
if
we have apartieular solution of the ISOLDEof Equation (13.14) and two
basis solutions of the HSOLDE, then the most general solution of (13.14) can be
expressed as the sum
of
a linear combiuation of the two basis solutions and the
particular solution.
We know how to find a second solution to the HSOLDE once we know one
solution. We now show that knowiug one such solution will also allow us to find a
particular solution to the ISOLDE. The method we use is called the
variation of
method
of
variation
constants. This methodcan also be used to finda second solutionto the HSOLDE.
of
constants
Let
hand
h be the two (known) solutions
of
the HSOLDE and
g(x)
the
sought-after solution to Equation (13.14). Write g as
g(x)
=
fl
(x)v(x)
and sub-
stitute it
in(13.14) to get a SOLDE for v(x):
" ( 2
f
{) ,
r
v +
p+-
v
=-.
h h
This is aftrst order liuear DE iu v', which has a solution
of
the form
v' =
W(x)
[c
+1
x
h(t)r(t)
dt]
ft(x)
a
W(t)
,
where
W(x)
is the (known) Wronskian
of
Equation (13.14). Substitutiug
W(x)
=
h(x)f5.(x)
-
h(x)f{(x)
=!:...
(h)
ft(x) ft(x)
dx
h
iu the above expression for v' and settiug C = 0 (we are interested in a particular
solution), we get
dv
=!:...
(h)
1
x
fl(t)r(t)
dt
dx dx
h a
W(t)
.».
[h(x)
1
x
h(t)r(t)
-l_
h(x)
!:...l
x
h(t)r(t)
dt
dx
h(x)
a
W(t)
fl(x).ax
a
W(t)
=ft
(x)r(x)/W(x)

13.4
THE
WRONSKIAN
361
and
V(X)
=
h(x)
r
Ji(t)r(t)
dt
_ (X
h(t)r(t)
dt.
fl(x)
Ja
W(t)
Ja
W(t)
This leads to the particular solution
1
x
fl
(t)r(t)
1
X
h(t)r(t)
g(x)
=
fl(x)v(x)
=
h(x)
W(t)
dt
-
fl(x)
W(t)
dt.
a a (13.16)
We have justproved the following result.
13.4.8. Proposition. Given a single solution
Ji(x)
of
the homogeneous equation
corresponding to an ISOLDE, one can use Equation (13.13) tofind a secondsolu-
tion
h(x)
of
the homogeneous equation and Equation (13.16) tofind a particular
solution
g(x).
The most general solution h will then be
h(x)
=
cdl
(x) +
czh(x)
+
g(x).
13.4.3 Separation and Comparison Theorems
The Wronskian can be used to derive some properties
of
the graphs of solutions of
HSOLDEs. One such property concerns the relative position
of
the zeros of two
linearly independent solutions of an HSOLDE.
the
separation
13.4.9.
Theorem.
(the separation theorem) The zeros
of
two linearly independent
theorem
solutions
of
an
HSOWE
occur alternately.
Proof
Let
Ji(x)
and
h(x)
be two independent solutions of Equation (13.12).
We have to show that a zero
of
Ji exists between any two zeros of
h.
The linear
independence of
fl
and h implies that W
(fl,
h:
x)
i'
0 for any x E [a, b]. Let
Xi
E [a, b] be a zero
of
h.
Then
o
i'
W(fI,
fz;Xi)
=
Ji(xilf~(Xi)
-
h(xilf{(xil
=
fl(Xi)f~(Xi)'
Thus, [: (Xi)
i'
0 and
f~(Xi)
i'
O.
Suppose that XI and
xz-where
X2
> Xl----are
two successive zeros
of
h.
Since h is continuous in [a, b] and
f~(xI)
i'
0, h has
to be either increasing
[f~(Xl)
> 0] or decreasing
[f~(XI)
< 0] at
XI.
For h to
be zero at
xz,
the next point,
f~
(X2)
must have the opposite sign from
f~
(Xl) (see
Figure 13.1). We proved earlier that the sign
of
the Wronskian does not change
in
[a, b] (see Proposition 13.4.2 and comments after it). The above equation then
says that
fl
(XI)
and
I,
(xz) also have opposite signs. The continuity
of
Ji then
implies that Ji must cross the x-axis somewhere between Xl and
xz.
A similar
argument shows that there exists one zero
of
h betweenany two zeros of
fl.
D
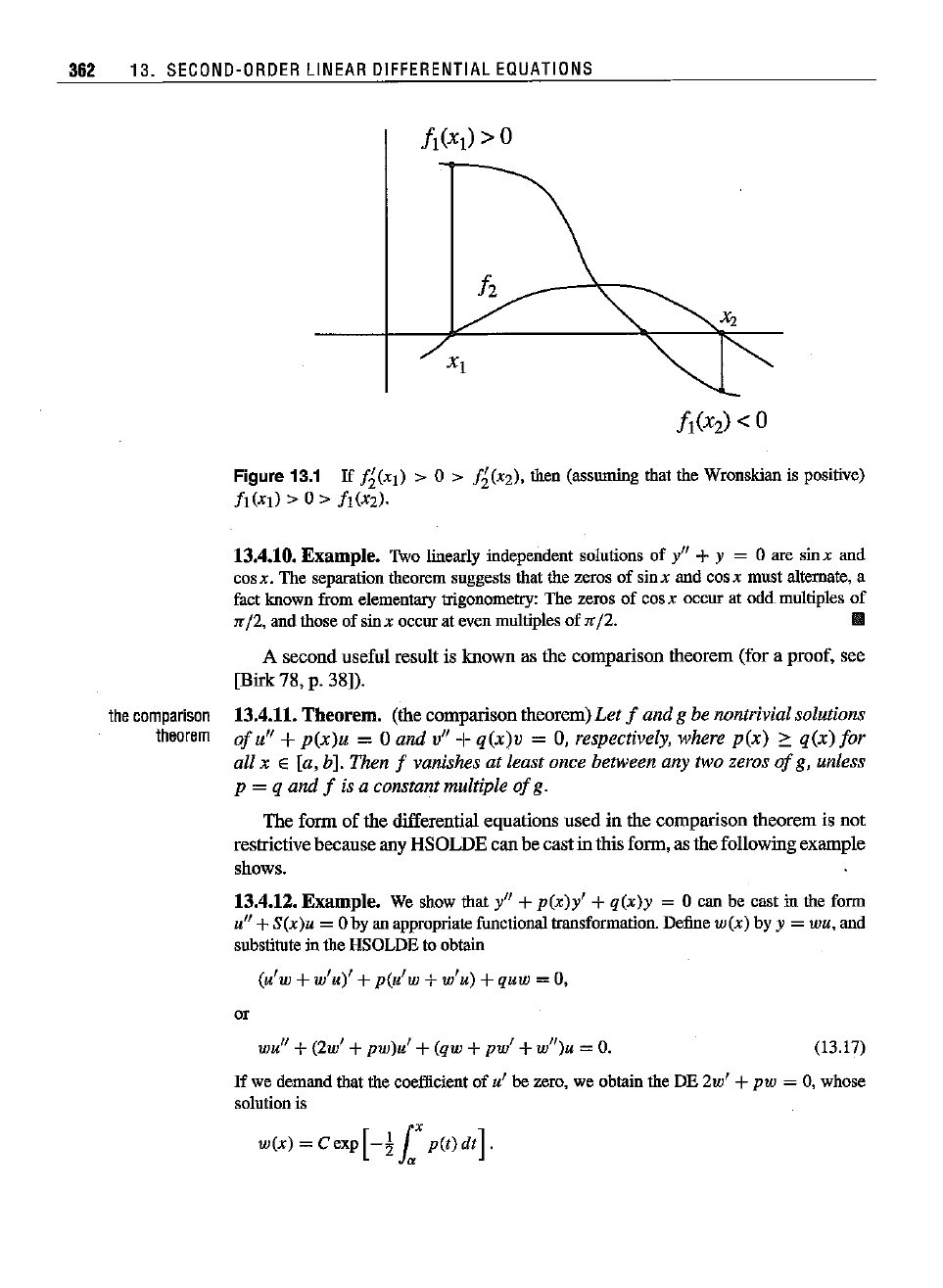
362 13.
SECOND-ORDER
LINEAR
DIFFERENTIAL
EQUATIONS
Figure 13.1 If 1
2
(xI ) > 0 > 1
2
(X2). then (assumingthaIthe Wronskianis positive)
!J(XI) > 0 > !J(X2).
the
comparison
theorem
13.4.10.
Example.
Two linearly independentsotntions of
v"
+ Y = 0 are sinx and
cosx. The
separation
theorem
suggests
that
thezeros of sinx andcosx must
alternate,
a
fact
known
from
elementary
trigonometry:
The zerosof cosx occuratodd,
multiples
of
"/2. and thoseof sinX occurat evenmultiples
of"
/2. ill
A second useful result is known as the comparison theorem (for a proof. see
[Birk 78. p. 38]).
13.4.11.
Theorem.
(the comparisontheorem)
Let
f and g be nontrivial solutions
of
u" +p
(x)u
= 0 and v" +q (x) v =
O.
respectively. where p(x)
2::
q(x)
for
all X E [a. b]. Then f vanishes at least once between any two zeros
of
g. unless
p
= q
and
f is a constant multiple
of
g.
The form
of
the differential equations used in the comparison theorem is not
restrictivebecause any
HSOLDEcan be castin this form. asthe following example
shows.
13.4.12.
Example.
We showthat y" +
p(x)y'
+
q(x)y
= 0 can be cast in the fonn
u" +
S(x)u
= Obyan
appropriate
functional
transformation.
Define
w(x)
by y =
WU,
and
substituteinthe
HSOLDE
to obtain
(u'w +w'u)' +p(u'w +w'u) +quw =
O.
or
wu" +(2w' +
pw)u'
+ (qw +
pw'
+ w")u =
O.
(B.i?)
If
we
demand
that
thecoefficient of u' bezero,we
obtain
theDE 2w' +
pw
= 0, whose
solution is
w(x)
=
cexp[-i
LX
p(t)dt].
