Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations

Подождите немного. Документ загружается.

when

Iz+il

< i·

11.3 ANALYTIC CONTINUATION 303

A consequence

this theorem is the following corollary.

11.3.2.

Corollary.

The behavior01afunction that is analytic in a region S c C is

completely determined by its behavior in a (small) neighborhood 01an arbitrary

point in that region.

analytic

continuation

This process

detetmining the behavior

an analytic function outside the

regionin whichit was originallydefinedis called

analytic

continuation.

Although

there are infinitely many ways

analytically continuing beyond regions

defi-

nition, the values

all functions obtained as a result

diverse continuations are

the sarne at any given point. This follows from Theorem 11.3.1.

Let

It,Iz :C

C be analyticin regions

and 82, respectively. Supposethat

and fzhave differentfunctional forms in theirrespective regions

analyticity.

there is an overlap between 81 and 82 and

= fzwithin that overlap, then

the (unique) analyticcontinuation

into 82

must

and vice versa.

fact,

we may regard

and h as a single function I :

C such that

I(z)

{!J(Z)

when ZE 81,

(z) when Z E 82.

Clearly,

I is analytic for the combined region 8 = 81 U 82. We then say that II

and fzare analytic continuations

one

another.

11.3.3.

Example.

Let us consider the function

(z)

= L~o

t",

which is analytic

for lel

< 1. We have seen that it converges to

1(1

- z) for

[z]

< 1. Thus, we have

(z) =1((1 - z) when

[z]

< I,

and!J

is not definedfor

Izi

> 1.

Now let us consider a second function,

h(z)

= L;:'=o

(~)n+1

(z + i)n, which

converges for [z +

To see what it converges to, we note that

h(z)

L~o

[~(z

i)]",

Thus,

h(z)

I-~(z+~)

I-z

Weobservethat although

(z) and h (z) havedifferentseriesrepresentations in the two

overlapping regions(seeFigure

11.7),theyrepresentthe samefunction,

I(z)

1(1-

z).

Wecan

therefore

write

{

fJ(z) when

Izl

< I,

(z) -

h(z)

when lz+

< i,

and

and h areanalyticcontinuations of ooe

another.

In fact,

I(z)

1(1

- z) is the

analyticcontinuation of both

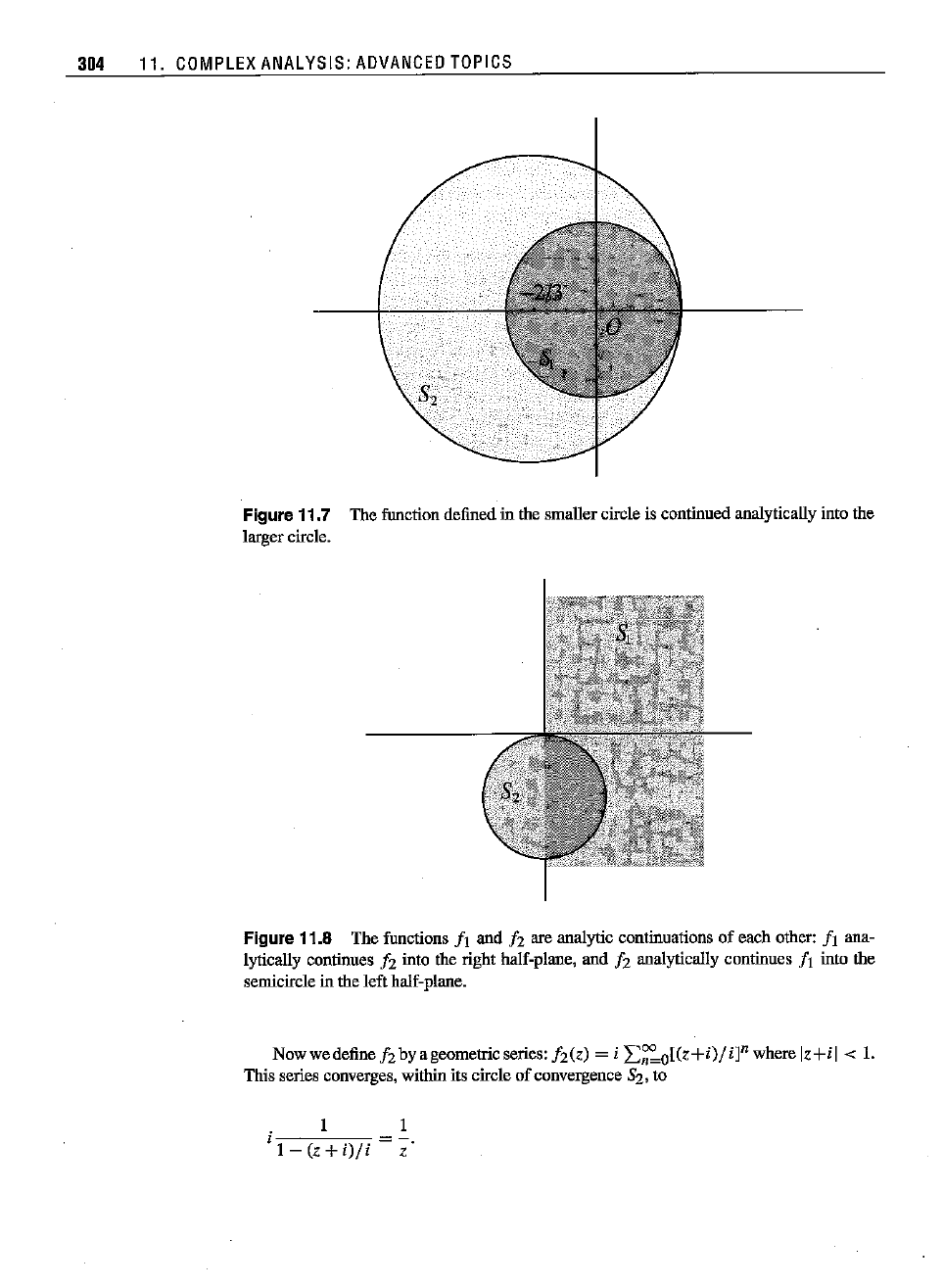
fJ and Iz for all of iCexcept z= 1. Figure 11.7sbowsSi,

theregion of definitionof Ii.for i = 1, 2.

III

11.3.4.

Example.

ThefunctionfJ(z) =1

dt existsonly

Re(z) > 0, in which

case

(z) =I(z.ItsregionofdefinitionSI is showninFigure H.S andissimplytheright

half-plane.

304 11.

COMPLEX

ANALYSIS:

ADVANCED

TOPICS

Figure11.7 The

function

defined

in the

smaller

circleis

continued

analytically

intothe

larger

circle.

Figure 11.8 The

functions

and

are

analytic

continuations

of each

other:

ana-

lytically continues

into the right half-plane, and

analytically continues !J into the

senticirc1ein the left half-plane.

Now we define

by a geometric series:

h(z)

= i

L:~O[(z+i)fi]n

where Iz+il <

This

series

converges,

within

itscircleof

convergence

82,to

. I I

=-.

l-(z+iJfi

(a)

11.3 ANALYTIC

CONTINUATION

305

(b)

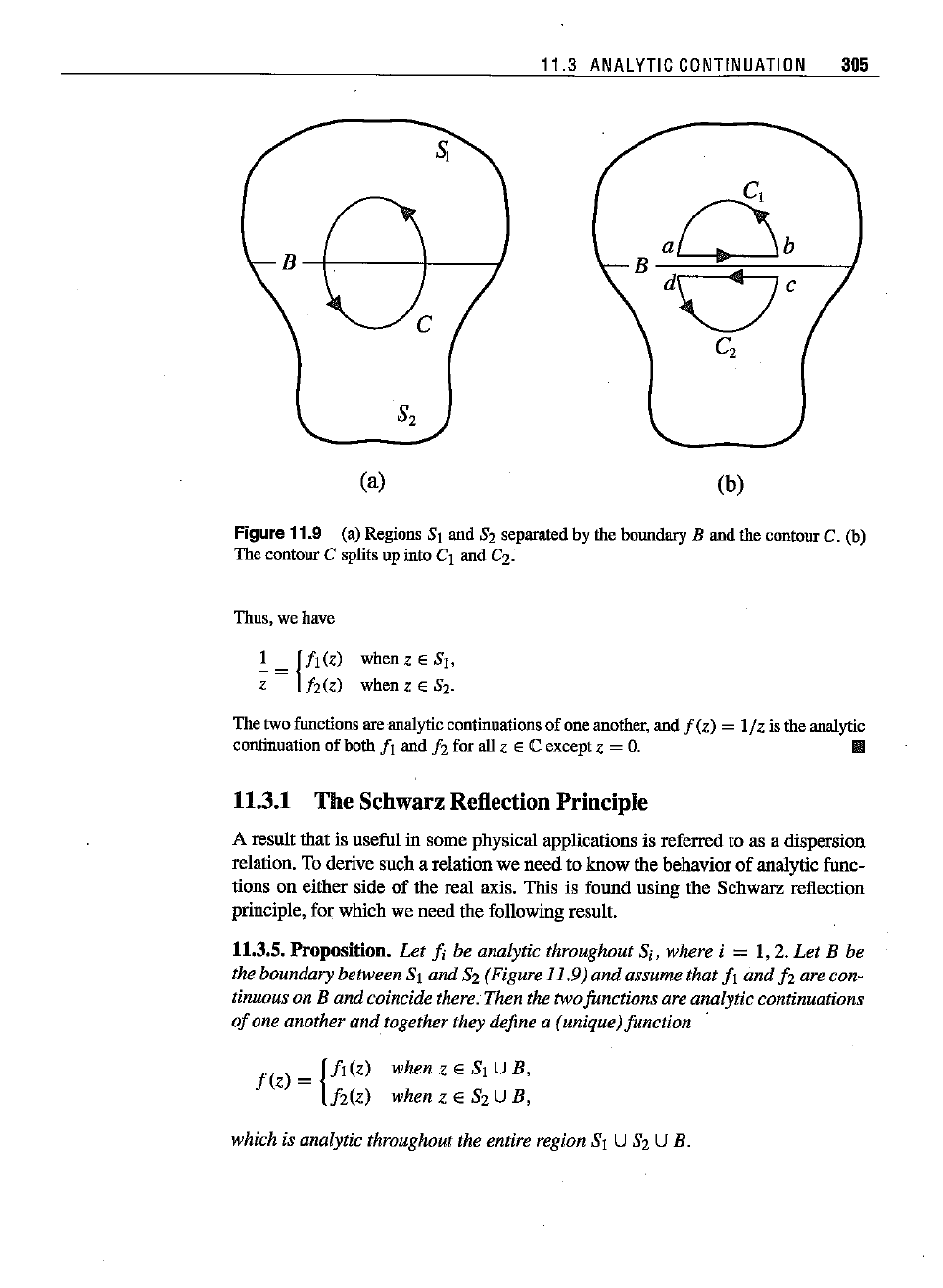
Figure 11.9 (a) Regions 81 and 82 separated by the bonndary B and the contnnr C. (b)

The

contour

C splitsupintoCl and

C2-

Thus,

wehave

~={ft(Z)

when z e Sj,

h(z)

when Z E 82.

Thetwo

functions

are

-analytic

continuations

of one

another,

andf (z) = 1/z is the

analytic

continoation of both II and

for

z E C except z =

iii

11.3.1 The SchwarzReflection Principle

A result that is useful in some physical applications is referred to as a dispersion

relation. Toderive such a relation we need to know the behavior

analytic func-

tions on either side of the real axis. This is found using the Schwarz reflection

principle, for which we need the following result.

11.3.5. Proposition. Let Ii be analytic throughout 8i, where i = I, 2. Let B be

the boundary between

81and 82 (Figure 11.9)

and

assume that

and

Izare con-

tinuous on B andcoincide

there.

Thenthetwofunctionsareanalyticcontinuations

one another and together they define a (unique)function

I(z)

{fl

(z) when z E 81 U B,

h(z)

when z E 82 U B,

which is analytic throughaut the entire region

81 U 82 U B.

306 11.

COMPLEX

ANALYSIS:

ADVANCED

TOPICS

Proof The proofconsists in showing that the function integrates to zero along any

closed curve in

Sl U S2 U B. Once this is done, one can use Morera's theorem to

conclude analyticity. The case when the closed curve is entirely in either

S; or S2

is trivial. When the curve is partially in Sj and partially in S2 the proof becomes

only slightly more complicated, because one has to split up the contour

C into Cl

and C2

Figure 11.9(b). The details are left as an exercise. D

Schwarz

reflection

principle

11.3.6.

Theorem.

(Schwarz reflection principle)

Let

f be a function that is ana-

lytic in a region

S that has a segment

the real axis aspart

its boundary B.

f(z)

is real whenever zis real, then the analytic continuation g

f into S* (the

mirror image

S with respect to the real axis) exists and is given by

g(z)

= f*(z*) where z E S*.

Proof First, we show that g is analytic in S*. Let

f(z)

u(x,

y) +

iv(x,

y), g(z) es

U(x,

y) +

iV(x,

y).

Then

f(z*)

fix,

-y)

u(x,

-y)

iv(x,

-y)

and g(z) = f*(z*) imply that

U(x,

y) =

u(x,

-y)

and

V(x,

y) =

-v(x,

-y).

Therefore,

au av av

= =

=---=-

ax ax ay

a(-y)

ay'

au av

= -

= ax = -""h'

These are the Cauchy-Riemann conditions for g(z). Thus, g is analytic.

Next, we note that

fix,

0) = g(x, 0), implying that f and g agree on the real

axis. Proposition 11.3.5 then implies that

f and g are analytic continuations of

one another. D

follows from this theorem that there exists an analytic function h such that

h(z) =

{f(Z)

when z E S,

g(z) when z E S*.

We note that

h(z*) = g(z*) =

f*(z)

= h*(z).

11.3.2 DispersionRelations

Let f he analytic throughout the complex plane except at a cut along the real axis

extending from

xo to infinity. For a point z not on the x-axis, the Cauchy integral

formula gives

f(z)

(2ni}-1

f(~)

I(~

- z) where C is the contour shown

in Figure 11.10. We assume that

f drops to zero fast enough that the contribution

11.3 ANALYTIC CONTINUATION 307

Figure 11.10 The contour used for dispersion relations.

from the large circletends to zero. The

reader

may

show

that

the contribution from

the small half-circle around

XQ also vanishes.

Then

[l""+i'

f(~)

l""-i'

f(~)

]

f(z)

-d~

2rn

xo+i'e

- Z

xo-ie

- z

[

roo

f(x

i~)

roo

f(x

if)

dX].

2nl

JXD

x - Z+

Jxo

X - Z - IE

Since z is not on the real axis, we can ignore the iE tenus in the denominators,

so that

f(z)

(2rri)-1

Jx':[f(x

if)

f(x

if)]dxj(x

- z).

The

Schwarz

reflection principle in

the

form

J*(z)

f(z*)

can

now

used

to yield

f(x

if)

f(x

if)

f(x

if)

J*(x

if)

=2i

Im[f(x

if)].

dispersion

relation

The final result is

1""

Im[f(x

if)]

f(z)

= - .

dx.

x-z

This is

one

form

dispersion

relation.

It expresses the value

a function at

any

point

the

cut

complexplane in terms

an integral

the

imaginary part

the function on the

upper

edge

the

cut.

When

thereare no residues in

the

UHP, we

can

obtainotherforms

dispersion

relations by equating the real

and

imaginary parts

Equation

(l0.11).

The

result

308 11.

COMPLEX

ANALYSIS:

ADVANCED

TOPICS

1 1

Im[f(x)]

Re[f(xo)]

±-P

dx,

-00

-xo

Im[f(xo)]

=F~P

Re[f(x)]

dx,

1T:

-00

x-xo

(11.6)

(11.7)

where the

upper

(lower) sign corresponds to placing the small semicircle around

xo in the

UHP

(LHP).

The

real

and

imaginary parts

as related by Equation

Hilbert

transform

(11.6), are sometimes sometiroes said to be the

Hilbert

transform

one another.

In someapplications the imaginary

part

f is an odd function

its argument.

Then the first equation in

(11.6)

can

be wtitten as

Im[f(x)]

Re[f(xo)]

±-P

dx.

x 0 x

2-x

To artive at dispersion relations, the following condition

must

hold:

lim

Rlf(Reie)1

= 0,

R->oo

. where R is the radius

the large semicircle in the

UHP

(or LHP).

f does

not

satisfy this prerequisite, it is still possible to obtain a dispersion relation called

dispersion

relation

dispersion

relation

with

one

subtraction.

This can

done

by introducing

with

one

subtraction

an extra factor

x in the denominator

the integrand. We start with Equation

0.15), confiningourselves to the

UHP

and assumingthatthere are no poles there,

so that the sum over residues is dropped:

f(X2) -

f(XI)

f(x)

dx,

- Xl

-00

(x - XI)(X - X2)

The

reader

may

checkthat by equating the real

and

imaginary parts on both sides,

letting

Xl = 0 and

= xo,

and

changing X to

-x

in the first

half

the interval

integration, we obtain

:....Re.:..o[::...f.:c.(x-",o)",]

= Re[f(O)] +

roo

Im[f(-x)]

roo

Im[f(x)]

dX].

xo n 1

x(x

+xo) 1

x(x

- xo)

For the case where

Im[f(

-x)]

-lm[f(x)],

this equation yields

Re[f(xo)]

= Re[f(O)] +

2x~

roo

Im~f(X)1

dx.

n 1

x(x

-xo)

11.3.7.

Example.

In optics. it has been shown that the imaginarypart of the forward-

optical

theorem

scatteringlightamplitudewithfreqnency00 isrelated,by the so-calledoptical theorem, to

thetotal crosssectionfor the absorptionof lightof that frequency:

!m[f(oo)] = -<1lot(oo).

411"

(11.8)

Kramers-Kronig

relation

11.4

THE

GAMMA

AND

BETA

FUNCTIONS

309

Substituting thisin Equation(t 1.7)yields

,,}

looo

O"totCw)

Re[f(wo)]

= Re[f(O)] +

----%:

p 2 2

da.

2:rr

(V-coO

Thus,the real part of the(coherent) forwardscatteringof light,that is, thereal part of the

indexcfrefraaion.canbecomputedfromEquation(11.8)byeithermeasuring orcalculating

O'tot(w),

the

simpler

quantity

describing

the

absorption

of lightinthe

medium.

Equation

(11.8)is the

original

Kramers-Kronigrelation. II

11.4 The Gammaand Beta Functions

We have already encounteredthe

gamma

function. In this section, we derive some

usefulrelations involvingthe

gamma

functionand the closelyrelatedbetafunction.

The

gamma

function is a generalization

the factorial

function-which

is defined

only for positive

integers-to

the system

complex numbers, By differentiating

the integral

1(01)

e-aldt

1/01

with respect to

repeatedly and setting

gamma

function

= I at the end, we get f

= nL This fact motivates the generalization

defined

r(z)

faoo

t,-Ie-Idt

for Refz) > 0, (11.9)

where

is called the

gamma

(or

factorial)

function.

is also called Euler's

integral

the second kind.

is clearfrom its definition that

r(n

+I) = n!

(11.10)

n is a positive integer.

The

restriction Re(z) > 0 assnres the convergence

the

integral.

An immediate consequence

Equation (11.9) is obtained by integrating it by

parts:

I'(z

+I) = zF'(z).

(11.11)

This also leads to Equation (11.10) by iteration.

Another consequence is the analyticity

I'(z),

Differentiating Equation

(11.11) with

respectto

z, we obtain

dr(z

+1)

r()

dr(z)

dz = z

+zdZ"

Thus,

dr(z)/dz

exists and is finite if and only

dr(z

I)/dz

is finite (recall

that z

0).

The

procednre

showing the latter is outlined in Problem 11.16.

Therefore, F'(z) is auaiytic whenever

I'(z

+1) is. To see the singularities

I'(z),

we note that

I'{z +n) =

z(z

l)(z

+2)

...

(z +n -

I)r(z),

310 11.

COMPLEX

ANALYSIS:

ADVANCED

TOPICS

F'(z} =

f(z

+n)

z(z +

l)(z

+2)

...

(z +n - 1)

(11.12)

The numerator is analytic as long as Re(z +n) > 0, or Retz) > r--Fl, Thus, for

Refz) >

-n,

the singularities of T'(z)

arethepolesatz

= 0,

-I,

-2,

...

-n+

Since n is arbitrary, we conclude that

11.4.1. Box. I'(z) is analytic at all Z E

except at z = 0,

-1,

-2,

...

where

I'(z)

has simple poles.

A useful result is obtained by setting z = !in Equation (11.9):

(11.13)

This can be obtained by making the substitntion u = .,fi in the integral.

We can derive an expressionfor the logarithmic derivative

the gammafunc-

tion that involves an infinite series. To do so, we use Equation (11.2) noting that

I'(z

+I) is an entire function with simple zeros at

{-k}~I'

Equation (11.2)

gives

where y is a constant to be determined. Using Equation (11.11), we obtain

(

= zeyZ

1+-

•

I'(z)

k~1

(11.14)

Euler-Mascheroni

To determine y, let z = 1 in Equation (11.14) and evaluate the resulting product

constant

numerically. The result is y = 0.57721566

...

, the so-called

Euler-Mascheroni

constant.

Differentiating the logarithm of both sides of Equation (11.14), we obtain

d 1

-in[f(z)]

- y +

--- .

dz Z

k=l

k z

(11.15)

(11.16)

where

Re(a),

Re(b) >

Other properties

the ganunafunction are derivable from the results presented

beta

function

defined

here. Those derivations areleftasproblems. The

beta

function, or

Euler's

integral

the first kind, is defined for complex numbers a and b as follows:

B(a, b) es

fal

(1 -

t)b-

1dt

(11.17)

11.4

THE

GAMMA

AND

BETA

FUNCTIONS

311

By changing I to 1/1, we can also write

R(a, b) sa 1

I-a-b(t

l)b-1dl.

Since 0 ::: I ::: I in Equation (11.16), we

can

define eby I = sin

e.This gives

["/2

R(a, b) = 2 J

sin

e cos

b- 1e

de.

(11.18)

(11.19)

gamma

function

and

beta

function

are

This relation can be used to establish a connection between the gamma and beta

functions. We note that

where in the last step we changed the variable to

x = .;t. Multiply

I'(c)

['(b)

and express the resulting double integral in terms of polar coordinates to obtain

['(a)[,(b)

['(a

+b)R(a, b), or

['(a)[,(b)

R(a, b) =

Bib,

a) = .

['(a

+b)

Let us now establish the following useful relation:

11:

[,(z)[,(1 - z) =

-.-.

SIDrr:Z

(11.20)

for 0

< Re(z) <

(11.21)

With a = z and b =

z, and using u = tan s, Equations (11.18) and (11.19)

give

(00

u2z~1

[,(z)[,(1 - z) =

R(z,

I - z) =2 J

Using the resultobtainedinExaruple 11.2.4, we immediatelyget Equation(11.20),

valid for 0

< Re(z) < I. By analytic continuation we then geueralize Equation

(11.20) to values

z for which both sides are analytic.

11.4.2. Example. Asanillustration oftheuseofEquation

(tt

.20),tetus showthat

(z)

canalsobe

written

1 1 [

r(z)

2:n:i

dt,

whereC isthecontourshownin Fignre11.11.FromEqoations (11.9)and

(tt

.20)it

follows

that

1 sin

sinrrz

i1rz

7l'Z

- =

--r(l

- z) =

«"

r-'dr

= - dr.

rez):n:

:n:

2:n:i

312

11.

COMPLEX

ANALYSIS:

ADVANCED

TOPICS

Im(t)

Figure 11.11 The

contour

Cusedin

evaluating

the

reciprocal

gamma

function.

The

contour

integral

Equation

(11.21) can be

evaluated

by noting

that

above

thereal

axis,

t =

rein

-r,

belowit t = re-i:n: =

-r.

and,as the

reader

maycheck,

that

the

contribution

from

thesmallcircleatthe

origin

zero;

loco

1°

-dt=

-.-(-dr)

+ .

(-dr)

C t

0 (re

l1T

(re-m)Z

loco

_e-

l1rz

el.7rZ

- dr.

o r

0 r

Comparison

withthelast

equation

aboveyieldsthe

desired

result.

III

Another useful relation can be obtained by combining Equations (11.11) and

(11.20):

r(z)r(1

- z) =

r(z)(

-z)r(

-z)

= rr/ sin zrz. Thus,

r(z)r(-z)

z sinzrz

(11.22)

Once we know

rex)

for positive values

real x, we can use Equation (11.22)

to find

rex)

for x <

Thus, for instance, r(!)

=.,fii

gives

r(-!)

= -2.,fii.

Equation (11.22) also shows that the gamma function has simple poles wherever

z is a negative integer.

11.5 Methodof SteepestDescent

is shown in statistical mechanics ([Hill 87, pp. 150-152]) that the partition

function, which generates

all the thermodynamical quantities, can be written as

a contour integral. Debye found a very elegant technique of approximating this

contour integral, which we investigate in this section. Consider the integral

(a)

eU!(z)

g(z)

(11.23)

where

lal is large and f and g are analytic in some region

C containing the

contour C. Since this integral occurs frequently in physical applications, it would