Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


11
_
Complex Analysis: Advanced Topics
The subject
of
complex analysis is an extremely rich and powerful area
of
math-
ematics. We have already seeu some
of
this richuess and power io the previous
chapter. This chapterconcludes our discussion
of
complexanalysis by iotroducing
some othertopics with varyiog degrees
of
importance.
11.1 Meromorphic Functions
Complexfunctions that have only simple poles as their siogularities are numerous
meromorphic
in applications and are called
meromorpbic
functions.
Inthis section, we derive
functions
an important result for such functions.
Assume
that!
(z) has simplepoles at{zj
}f~l'
where N couldbe iofinity. Then,
if
z
01
Zj for all
j,
the residue theorem yields!
~
( !CI;) dl; =
!CZ)+
tRes
eCI;))
,
2Jfl
len
I; - Z
j=!
I; - Z
~=Zj
where C
n
is a circle contaioiog the first n poles, and it is assumedthatthe poles are
arranged in order
of
iocreasiog absolute values. Since the poles
of
! are assumed
to be simple, we have
(
!
~
)
)
.
!~)
1 .
Res
--
= Inn
CI;
-
Zj)--.
=
--
lim
[CI;
-
zj)!CI;)]
I; - Z
~=Zj
~""Zj
I; - Z
Zj
- Z
~""Zj
1
r'
=
--Res[!Cf;)]~~Zj
es
_J_,
Zj
- Z
Zj
- Z
INote
that
the
residue
of
f(~)/(~
- z) at'; = z is simply
f(z),

294 11.
COMPLEX
ANALYSIS:
ADVANCED
TOPICS
where rj is, by definition, the residue
of
f(~)
at
~
=
ij.
Substituting in the
preceding equation gives
f(z)
=
~
(
f(~)
d~
-
t~.
2:",
Je,
~
- Z
j~l
Zj - Z
Taking the difference between this and the same equation evaluated at Z = 0
(assumed to be none
of
the poles),Z we
can
write
(11.1)
Mittag-Leffler
expansion
f(z)
- f(O) =
-f--,
(
H~(~»
d~
+t
rs
(_1_
+
2.)
.
7Cl
len
- Z
)=1
Z -
Zj Zj
If
If(~)1
approaches a finite value as
I~I
--..
00,
the integral vanishes for an infinite
circle (which includes all poles now),
and
we obtain
what
is called the
Mittag-
Leffler
expansion
of
the meromorphic fuoction
f:
f(z)
=
f(O)
+
trj
(_1_
+
2.).
)=1
Z -
Zj Zj
Now
we let g be an entire function
with
simple zeros. We claim that (a)
(dg/dz)/g(z)
is a meromorphic function that is bounded for all values
of
z, and
(b) its residues are all unity. To see this, note that g is
of
the fomr'
g(z)
= (z - ZI)(Z -
zz)···
(z -
zN)f(z),
where
Zl,
...
, ZN are all the zeros
of
g,
and
f is an analytic function that does
not
vanish anywhere in the complex plane.
It
is now easy to see that
g'(z)
N I
f'(z)
g
(z)
= L z -
z·
+
f(z)
.
J=l
j
This expressionhas bothproperties (a)
and
(b) mentionedabove. Furthermore, the
last term is an entire function that is bounded for all
C. Therefore, it
must
be a
constant by Proposition
9.5.5.This derivation also verifies Equation (11.1),which
in the case at
hand
can be written as
d s'(z) d N
(I
I)
-d
Ing(z)
=
-(
) =
-d
Ing(O)+
L
--
+- ,
z g z Z
j~l
Z - Zj Zj
whose solution is readily found to be
g(Z) = g(O)e
CZ
fI
(I
-
~)
e
Z
/
Zj
)=1
z)
and it is assumed that Zj
i=
0 for all
j,
where
(dg/dz)lz~o
c=
g(O)
(11.2)
~This
is not a restrictive assumption because we can always move our coordinate system so that the origin avoids allpoles.
One can ''prove'' this by factoring the simple zeros one by one, writing
g(z)
= (z -
Zl)!t
(z) and noting that g(Z2) = 0,
with Z2
i=
at.
implies that
il
(z) = (z - Zz) h (z), etc.
(a)
11.2
MULTIVALUED
FUNCTIONS
295
(b)
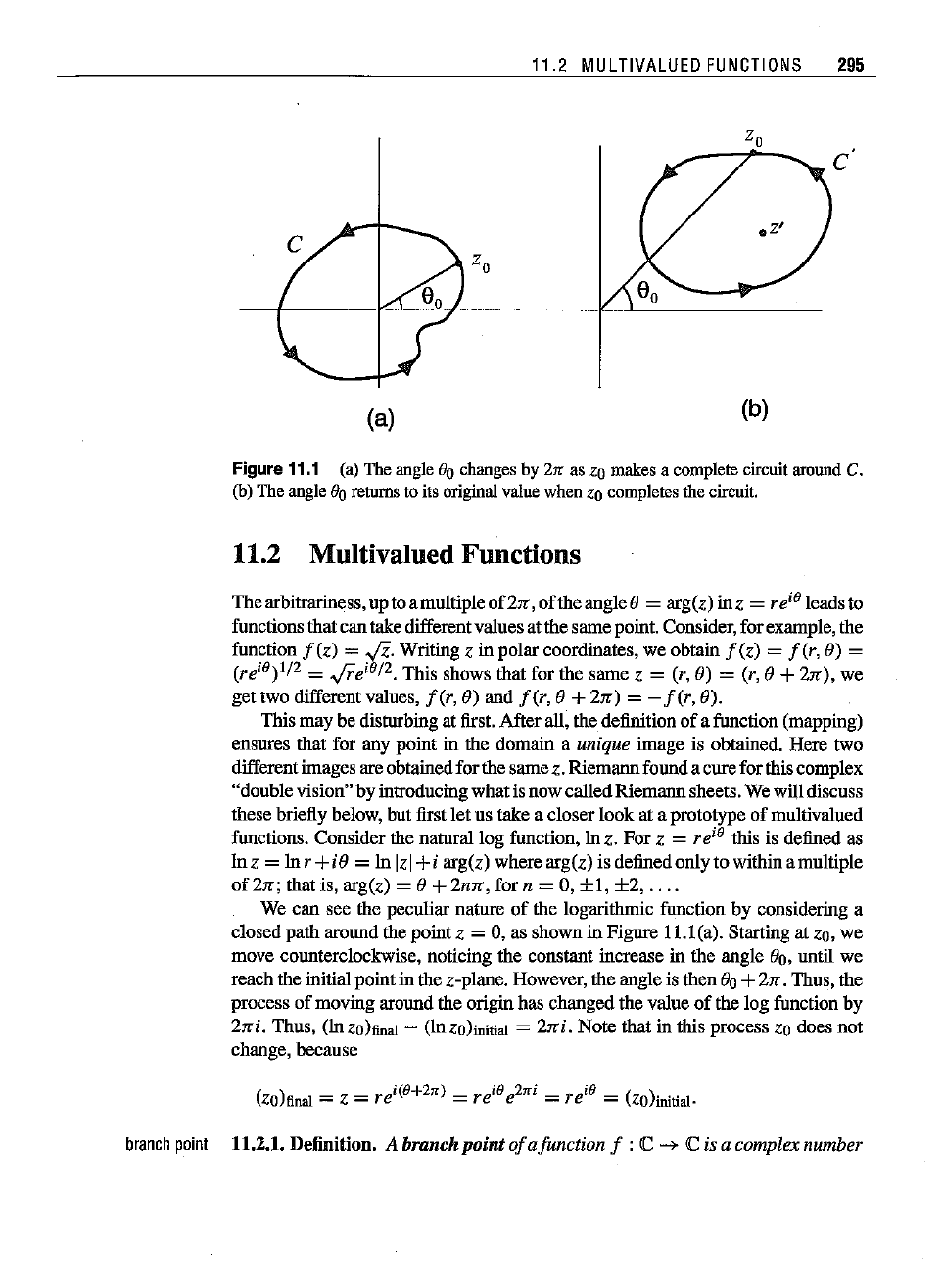
Figure 11.1 (a)Theangle
eO
changes
by
2rr
as ZQ
makes
a
complete
circuit
around
C.
(b)Theangle80
returns
toits
original
valuewhen
zQ
completes the
circuit.
11.2 Multivalued Functions
The arbitrariness,upto a multiple
of2".,
ofthe angle 0 = arg(z)
inz
= re
ie
leads to
fuuctions that can take differentvaluesat the same point. Consider, for example, the
function
!(z)
=
.,ji..
Writing z in polar coordinates, we obtain
!(z)
=f tr, 0) =
(re
ie
)t/2 = ..;re
ie
/
2
.
This shows that for the same z = (r,O) = (r,O + 2".), we
get two different values,
f tr,0) and f'(r, 0 + 2".) = -
!(r,
0).
This may be disturbing at first. Afterall, the definition
of
a function (mapping)
ensures that for any point in the domain a
unique image is obtained. Here two
differentimages are obtainedfor the same z. Riemannfound a cure for this complex
"doublevision" by introducingwhatis now calledRiemannsheets. We will discuss
these briefly below, but first let us take a closer look at a prototype of multivalued
functions. Consider the natural log function,
Inz. For z = re
ie
this is defined as
In z
=In r+iO =In
[z]
+i
arg(z) where arg(z) is defined only to within amultiple
of
2".; that is, arg(z) = 0 + Znit , for n = 0,
±l,
±2,
....
We
can
see the peculiar nature
of
the logarithmic function by considering a
closed path around the point
z = 0, as shown in Figure 11.1(a). Starting at
Zo,
we
movecounterclockwise, noticing the
constant
increase
in the angle
(}o,
untilwe
reach the initial pointin the z-plane. However, the angle is then 00+ 2".. Thus, the
process
of
moving around the origin has changed the value
of
the log function by
2".i. Thus, (lnzo)final - (lnzo)mitiol
= Zati. Note that in this process zo does not
change,
because
branch
point
11.2.1. Definition. A branchpoint
of
afunction f :
iC
->
iC
is a complex number

296 11.
COMPLEX
ANALYSIS:
ADVANCED
TOPICS
zo
with the property that
f(ro,
110)
oft
f(ro,
1I
0 +
211")
for
any closed curve C
encircling Z00Here (ro,
110)
are the polar coordinates
ofzo.
Victor-Alexandre Pniseox (1820-1883) wasthe firsttotakeup thesubjectofmultivalued
functions.
In 1850
Puiseux
published
a
celebrated
paper
on
complex
algebraic
functions
givenby f (u, z)= 0, f a
polynomial
inu andz.He
first
made
clearthe
distinction
between
polesandbranchpoints
that
Cauchy
had
barely
perceived,
and
introduced
the
notion
ofan
essentialsingularpoint,towhich
Weierstrass
independently
hadcalled
attention.
Though
Cauchy,
inthe1846
paper,
did
consider
the
variation
of
simple
multivalued
functions
along
paths
that
enclosed
branch
points,
Puiseux
clarified
this
subject
too.
Puiseux
also
showed
that
the
development
ofa
function
ofz
about
a
branch
point
z = a
must
involve
fractional powers of z - a. He then
improved
on
Cauchy's
theorem
on the
expansion
of a
function
in a
Maclaurin
series.
By his
significant
investigations
of
many-
valued
functions
and
their
branch
points
in the
complex
plane,
andby his
initial
work
on
integrals
of such
functions,
Puiseux
brought
Cauchy's
pioneering
work
in
function
theory
to the end of whatmightbe calledthe firststage.The difficnlties in the thenryof multiple-
valued
functions
and
integrals
ofsuch
functions
werestilltobe
overcome.
Cauchy
did
write
other
papers
onthe
integrals
of
multiplevalued
functions
inwhichhe
attempted
to follow
upon
Puiseux's
work;
and
though
he
introduced
the
notion
of
branch
cuts(!ignes
d~
arrh),
be wasstill
confused
about
the
distinction
between
poles
and
branch
points.
This
subject
of
algebraic
functions
and
their
integrals
wastobe
pursued
by
Riemann.
Puiseux
wasakeen
mountaineer
andwasthe
first
to scalethe
Alpine
peak
that
is now
namedafter
him.
Thus,Z = 0is a branch
point
of
the logarithmicfunction. Studyingthe behavior
of
1n(I/z) =
-Inz
around z = 0 will reveal that the point
"at
infinity" is also
a branch
point
of
Inz. Figure 11.1(b) shows that any other
point
of
the complex
)lIane, such as
z',
carmot be a branch
point
because
110
does
not
change when C' is
traversed completely.
11.2.1 Riemann Surfaces
branch
cut
or
simply
"cut"
The idea
of
a Riemarm surface begins
with
the removal
of
all points that lie on the
line (or any othercurve) joiningtwo branchpoints. For
Inz this means the removal
of
allpoints lying on a curve that starts at Z = 0 and extends all the way to infinity.
Such
a curve is called a
branch
cut,
or simply a cut.
Let
us concentrate on Inzand take the
cut
to be along the negative
half
of
the
real axis.
Let
us also define the functions
fn(z) =
I«
(r, II)
=
Inr
+i(1I+
2n1l")
for - 1C < e<
1C;
r > 0; n = 0,
±1,
...
,

Riemann
surfaces
and
sheets
11.2 MULTIVALUED
FUNCTIONS
297
so
in
(z) takes on the same values for -:rr: < e < n that Inz takes in the range
(2n -
I):rr:
< e < (2n +
I):rr:.
We have replaced the multivalued logarithmic
function by a series of different functions that are analytic in the cut z-plane.
This process of cutting the z-plane and then defining a sequence of functions
eliminates the contradiction causedby the existence
of
branchpoints, since we are
no longer allowed to completely encircle a branch point. A complete circulation
involves crossiogthe cut, which, in tum, violates the domainof definitionof
in
(z).
We have made good progress. We have replacedthe (nonanalytic) multivalued
function In
Z with a series of analytic (in their domain
of
definition) functions
in
(z). However, there is a problem left:
in(z)
has a discontinuity at the cut.
In
fact,
just
above the cut in(r,:rr: - E) =
Inr
+i(:rr: - E +2n:rr:) with s c- 0, and
just
below it
in(r,
-:rr: +
E)
=
Inr
+i(-:rr: +E +
2n:rr:),
so that
lim
[in(r,:rr: - E) -
in(r,
-:rr: +E)l =
2:rr:i.
' ....0
To cure this we make the observation thatthe value of
in
(z)
just
above the cut
is the same as the value of in+1
(z)
just
below the cut. This suggests the following
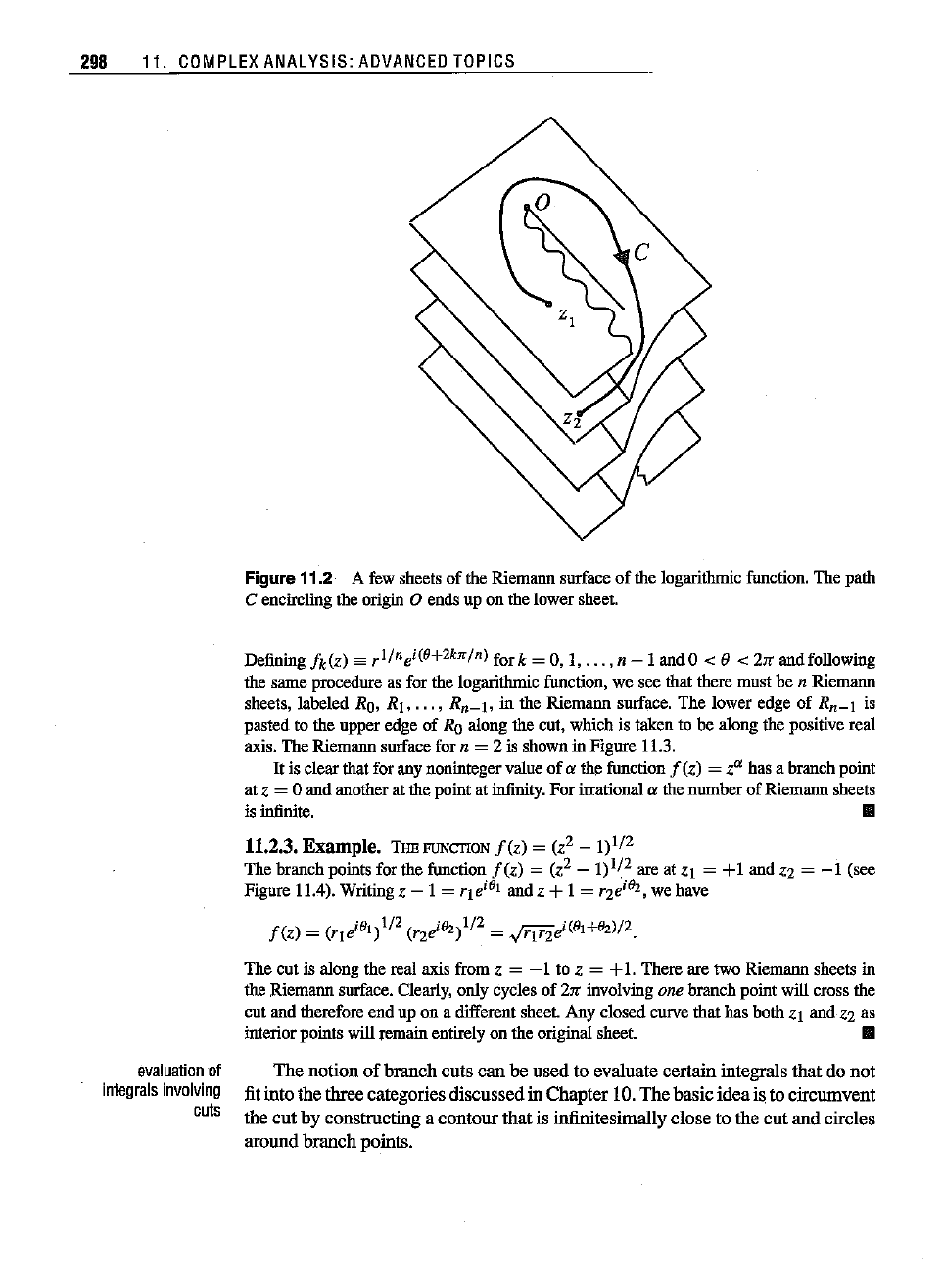
geometrical construction, due to Riemarm: Superpose an infinite series
of
cut
complex planes one on top of the other, each plane corresponding to a different
value of
n.The adjacent planes are connected along the cut such that the upper lip
of the cut in the
(n -
I)th
plane is connected to the lower lip of the cut in the
nth
plane. All planes containthe two branch points. That is, the branch points appear
as "hinges" at which all the planes are joined. With this geometrical construction,
if we cross the cut, we end up on a different plane adjacent
to the previous one
(Figure 11.2).
The geometric surface thus constructed is called a
Riemann
surface;
each
plane is called a
Riemann
sheet
and is denoted by
R],
for j = 0,
±I,
±2,
....
A single-valued function defined on a Riemarm sheet is called a
branch
of the
original multivalued function.
We have achieved the following: From a multivalued function we have con-
structed a sequence of single-valued functions, each defined in a single complex
plane; from this sequence of functions we have constructed a single complex func-
tion definedon a single Riemarm surface. Thus, the logatithmicfunction is analytic
throughout the Riemarm surface except at the branch points, which are simply the
function's singular points.
It
is now easy to see the geometrical significance
of
branch points. A complete
cycle around a branchpointtakes us to anotherRiemarm sheet, where the function
takes on a differentform.
On the other hand, a complete cycle around an ordinary
point
either
nevercrossesthecut,orif it does,it will crossit backto the
original
sheet.
Let us now briefly consider two of the more common multivalued functions
and their Riemarm surfaces.
11.2.2.
Example.
THE
FUNCTION
f(z)
=
z'!"
The onlybranchpointsfor the functioo
f(z)
=
zl/n
are z = 0 and the point at
infinity.
298 11.
COMPLEX
ANALYSIS:
ADVANCED
TOPICS
Figure 11.2- A few sheets
of
the Riemann surface
of
the logarithmic function. The path
C
encirclingtheorigin 0 ends up on the lower sheet.
Defioing
!k(z)
sa r
1
/
nei
(9+2k"
jn)
for k = 0, 1,
...
,n
-1
and0 < e< 2". andfollowing
the
same
procedure as for the logarithmic function, we see that there must be n Riemann
sheets, labeled Ro. RI
•...
,
Rn-l.
in the Riemann surface.
The
lower edge of
Rn-l
is
pasted to the upper edge
of
Ro along the cut, which is taken to be along the positive real
axis.The Riemannsurfacefor n = 2 is showninFigure 11.3.
It
is c1earthatfor any nonintegervalue
of
a the function
fez)
=
zOl.
has a branch point
at z
= 0 and another at the point at infinity.
For
irrational a the
number
of
Riemann sheets
is infinite.
II
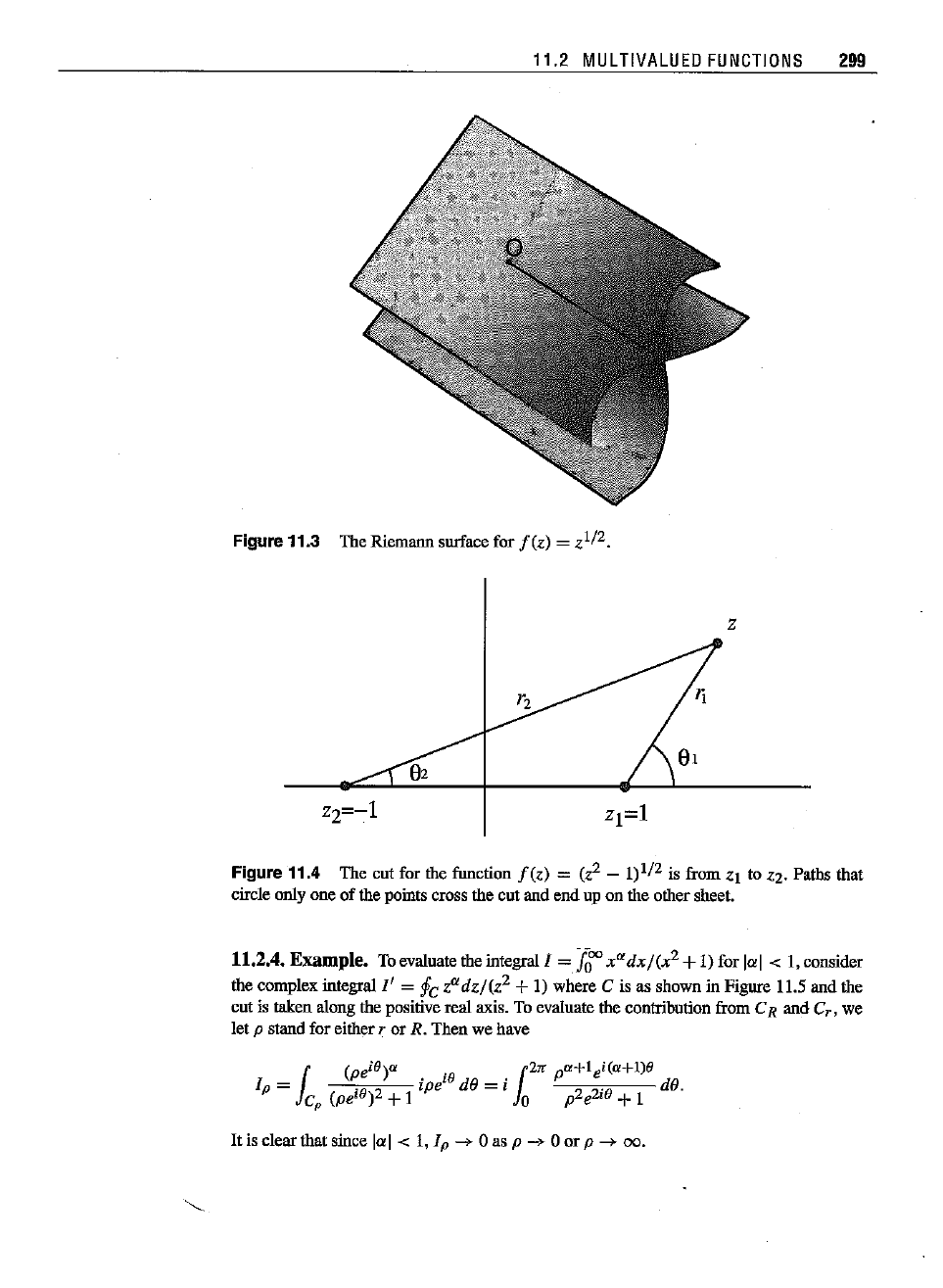
11.2.3.
Example.
l'HEFUNCTION
f(z)
= (z2
_1)1/2
The brancbpointsfor the function
f(z)
= (z2 - 1)1/2 are at zt = +1 and Z2 =
-1
(see
Figure 11.4).Writingz - 1 = rt ie, andz + 1 = r2eie,. we bave
f(z)
= (Yje
ie
1)1/2
(r2eie,)I/2
= .jYj
r
2ei
(e
1
+e,)/2.
The
cut
is along the real axis from z =
-1
to z = +1. There are two Riemann sheets in
the Riemann surface. Clearly, only cycles
of
2rr involving one branch point will cross the
cut and therefore
end
up on a different sheet.
Any
closed curve that has
both
zr and Z2 as
interiorpoints will remain entirely on the original sheet.
II
evaluation
of
integrals
involving
Guts
The
notion
of
branch cnts
can
be used to evalnate certain integrals that do
not
fitinto the three categories discussedin Chapter 10.
The
basic
idea
is to circumvent
the
cut
by constructing a contour thatis infinitesimally closeto the
cut
and
circles
around branchpoints.
11.2 MULTIVALUED
FUNCTIONS
299
Figure
11.3 The Riemann surface
for
fez)
=
zl/2.
z
Figure
11.4 The cut for the fuoction
fez)
= (z2 - 1)1/2 is from ZI to Z2. Paths that
circle only one of the points cross the cut and end up on the other sheet.
11.2.4.
Example.
To evaluate the
integrall
=
10
00
x
adx/(x
2
+ I) for
lal
< I, consider
the complex integral
t'
=
:Fe
z
adz/(z2
+1) where C is as shown in Figure 11.5 and the
cut is taken along the positive real axis. To evaluate the contribution from C
R and Cr, we
let p stand for either
T or R.
Then
we have
It
is clear that since lal < 1, I
p
-+
0as p -)- 0or p
-+
00.

300 11.
COMPLEX
ANALYSIS:
ADVANCED
TOPICS
(11.3)
Figure 11.5 The
contour
fortheevaluation
ofthe
integrals
ofExamples 11.2.4and11.2.5.
The
contributions
from L1 and £2 do not cancel one
another
because the value of
thefunctionchangesaboveandbelow thecut. To
evaluate
these two
integrals
we haveto
choose a
branch
of the
function.
Let us choose
that
branch
on which
ZCl
=
Izlfte
iaB
for
o< () < 2Jt. Along
L1,
(J
~
0 or zet =
x",
andalong
L2.
e
~
2rr
or zet = (xe
27ti)a'.
Thus,
i
z·
looo
x'
1°
x
ct
e
2rria
--4Z=
--dx+
. dx
C
z2 +I 0 x
2
+I
00
(xe
2
n')2
+I
= (1 - e
21r
i
Cl.
)
tX)
~
dx,
10
x
2
+I
TheLHSof this
equation
canbe
obtained
usingthe
residue
theorem.
There
are
twosimple
poles, at z =
+i
and z =
-i
with residues
Res[f(i)]
= (e
in/
2).
/2i
and
Res[f(-i)]
=
_(ei3n/2).
/2i. Thus,
1i
z·
(e
i•
n/2
e
i3
•
n/
2)
. .
--
dz = 2rci
--.
- -
--.-
=
rt(e
w rrj2
_ eI3car/2).
cz
2
+ 1
21 21
Combiniog this with Equation (11.3), we obtaio
[00
~
dx = 7r(eicmj2 - <3urr/2) =
!!:.
sec a7r .
io xl + 1 1-
e~bna
2 2
If
we hadchosena
different
branch
of the
function,
boththeLHSandtheRHSof
Equation
(11.3) wonld have been different, but the
fina1
result would stiDhave been the same.
III

11.2
MULTIVALUED
FUNCTIDNS
301
Ce
for 0 < a < 1.
(11.4)
III
(11.5)
Figure 11.6 The contourfor the evaluation
of
the integral
of
Example
11.2.6.
11.2.5. Example.
Here
is another integral involving a branch cut:
1=
roo
x-a
dx
1
0
x+
I
To evaluate this integral we use the zeroth branch
of
the function
and
the contour
of
the
previousexample (Figure 11.5).Thus, writing z = peW. we have
2"iRes[f(-I)]
=
J:
z-a
dz =
[00
p-a
dp +
J:
z-a
dz
Ic z + I 1
0
p + I
fCR
Z + I
1
0 (pe
2
i,,)-a.
i c
a
+ . e
2
mdp+
--dz.
00
pe
Zm
+ 1 C
r
Z + 1
The contributions from
both
circles vanish by
the
same
argument
used
in the previous
example. On the other hand,
Res[f(
-I)]
=
(_I)-a.
For
the
branch we are using,
-I
=
e
i".
Thus,
Res[f(
-I)]
=
e-
i
a".
The RHS
of
Equation
(11.4) yields
10
00
-a
10
00
-a
_P_
dp -
e-
2ina
..!!...:.....-
dp = (1 _
e-
2i1t
a)I.
o
p+1
0
p+1
It
follows from (11.4) that (1 -
e-
2i
Jr
a)I
=
21rie-
i 1rQ
,
or
10
00
x-a
1C
dx
- for 0 < a < 1.
o
x+l
- sinarr
11.2.6.
Example.
Let us evaluate I = f
o
oo
Inx
dx/(x
2
+a
2)
with
a >
O.
We choose the
zeroth
branch
of
the logarithmic function, in
which
-li
< 9 <
Jr,
and
use the contour
of
Figure 11.6. For
Ll'
Z = pe
i1r
(note that p > 0),
and
for
£2,
Z= p. Thus, we have
i
lnz
1<
In(pe;").
/,
ln z
2"i
Res[f(ia)]
=
-2--2
dz = . 2 2
e"
dp
+
~
dz
C z
+a
00 (pe
lJt
)
+a
C" z
+a
1
00
lup
/,
Inz
+
-2--2
dp +
~
dz.
E p
+a
CR z
+a

302
11.
COMPLEX
ANALYSIS:
ADVANCED
TOPICS
wherez= ia is theonlysingularity-a simple
pole-in
the
UHP.
Now we notethat
l
E
In(pei:Jr).
1
00
lop
+
itt
1
00
lop
. 1
00
dp
. e
l1C
dp =
dp=
---dp+zJr
---.
00
(
pe
l'lr)2
+a
2
to p2
+a
2
E p2
+a
2
to p2
+a
2
The
contributions
from
thecirclestendto
zero.
Onthe
other
hand,
Inz
In(ia)
1 (
''')
Res[f(ia)]
= lim (z -
ia)
. . =
-.
- =
-.-
Ina
+!-
.
z-via (z -
w)(z
+ za) 2za 'Iia 2
Substituting
thelasttwo
results
in
Equation
(11.5), we
obtain
?:'(lna+i::')=21°O
;llP
1 dp +i:7r1
00
zd
p
2"
a 2 E P
+a
E p
+a
It
canalsoeasilybe shownthatI
o
oo
dp/(p2
+a
2)
=
,,/(2a).
Thus,in thelimitE
-+
0, we
get I =
!!..-In
a. The sign of a is
irrelevant
becauseit
appears
as a
square
in the
integral.
2a
Thus,
we canwrite
1
00
Inx n
-2--2
dx = -21Ilnlal,
D x
+a
a
a
i'
O.
equal
ona
piece,
equal
all
over
n.3
Analytic Continuation
Analytic functions have certainunique properties, some
of
whichwe have already
noted.
For
instance, the Cauchy integral formula gives the value
of
an analytic
function inside a simple closed contour once its value on the contour is known.
We have also seen that we can deform the contours
of
integration as long as we do
not encounter any singnlarities
of
the function.
Combining these two properties and assuming that
f : C
-+
C is analytic
within a region
See,
we can ask the following question: Is it possible to extend
f beyond S1 We shall see in this section that the answer is yes in many cases
of
interest."
First
consider
1I.3.1. Theorem. Let
fl'
fz :C
-+
C be analytic in a region S.
If
fl
=
I:
in a
neighborhood
of
a point z E S, orfor a segment
of
a curve in S, then
I,
= fzfor
allz E S.
Proof
Let g = f1- fz,and U = {z E S Ig(z) =
OJ.
Then U is a subset
of
S that
includes the neighborhood
of
z (or the line segment) in which
fl
=
h.
If
U is the
entireregionS, we are done. Otherwise,
U has a boundarybeyondwhichg(z)
oF
O.
Since all points within the boundary satisfy g(z) = 0, and since g is continuous
(more than that, it is analytic) on S,
g must vanish also on the boundary.
But
the
bouodarypoints are not isolated: Any smallcirclearound
anyone
of
themincludes
points
of
U as well as points outside U. Thus, g must vanish on a neighborhood
of
any boundary point, implying that g vanishes for some points outside U. This
contradicts our assumption. Thus,
U must include the entire region S. 0
4Provided
that
S is not discrete (countable). (See [Lang85, p. 91].)
