Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


10.3 EVALUATION
OF
DEFINITE
INTEGRALS
283
10.3.4 Some OtherIntegrals
The three types of definite integrals discussed above do not exhaust all possible
applications of the residue theorem. There are other integrals that do not fit into
any of the foregoing three categories but are still manageable. As the next two
examples
demonstrate,
aningenious choiceof
contours
allows
evaluation
of
other
types of integrals.
10.3.8.
Example.
Letus evaluate the Gaussianintegral
1
00
. 2
I = e
la
x-
bx
dx
-00
where a, b E
lll.,
b >
O.
Completing
squares
intheexponent, we have
1=
1
00
e-
b[x-ia/(2b)]2_
a2j4b
dx
=
e-
a2/
4b
lim l
R
e-
b[x-ia/(2b)]2
dx.
-00
R-?oo
-R
If
we
change
the
variable
of
integration toz = x - iaf(2b), we
obtain
2/(4b) l
R
-
ia
/ (2b) b
2
1=
e-alim
e?
Z dz.
R-+oo
-R-iaj(2b)
Let usnow defineIR:
l
R
-
ia
/(2b)
2
[R es
e-
bz
dz.
-R-ia/(2b)
This is an integralalonga straightline Ci that is parallelto the x-axis (seeFigure
10.4).
We close the
contour
as shownandnote
that
e-
hzZ
is analytic
throughout
the
interior
of
theclosed
contour
(it is anentirefunction!). Thus,the
contour
integral
mustvanishby the
Cauchy-Gaursat
theorem.
So we
obtain
[
2
i:
2 1 2
IR +
e-
bz
dz
+
e-
bx
dx
+
e-
bz
dz
=
O.
C3 R C4
AlongC3, z =R + iy and
r
e-bz2dz=1°
e-b(R+iy)2idY=ie-bR21°
eby2-2ibRYdy
lc,
-ia/(2b)
-ia/(2b)
whichclearlytendsto zeroas R --+
00.
We get a similarresultfor theintegral along C4.
Therefore,
we have
l
R
2
IR =
e-
bx
dx
-R
Finally,
we get
. 1
00
_bx
2
~
=}
11m
IR = e
dx
= -b'
R~oo
-00
III
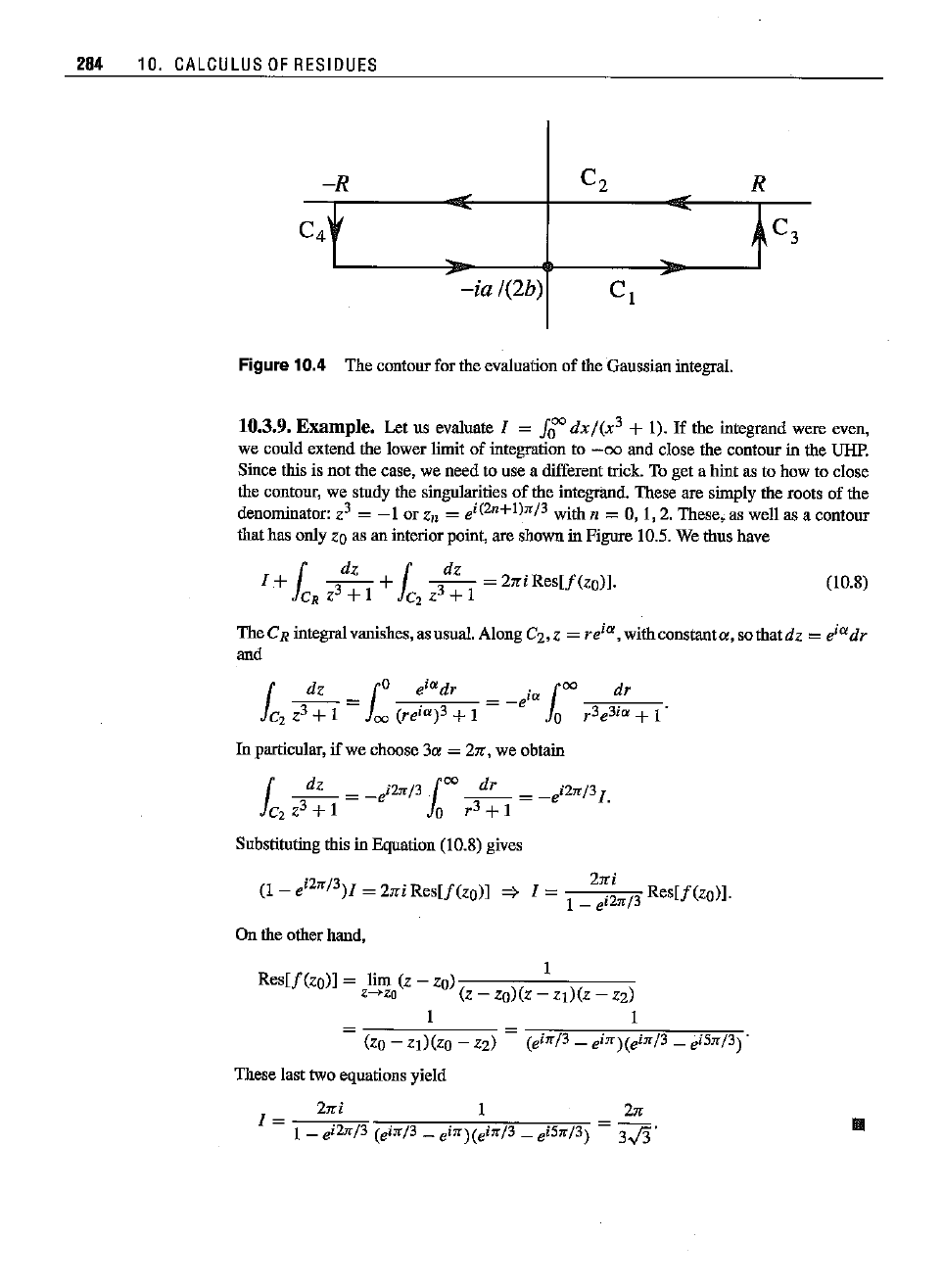
284 10,
CALCULUS
OF
RESIDUES
-R
-ia
1(2b) C I
Figure 10.4 The contourfor the evaluation
of
the
Gaussian
integral.
R
10.3.9.
Example.
Let us evaluate [ = fo
oo
dxl(x
3
+
I).
If
the integraud were even,
we could
extend
the lower limit
of
integration to
-00
and
close the contour in the UHP.
Since this is
not
the case, we
need
to use a different trick. To
get
a hint as to how to close
the contour, we study the singularities
of
the integrand. These are simply the roots of the
denominator: z3
=
-1
or
Z,~
= e
i
(2n+ l)
1l'
j3
with
n =0,
1,2.
These, as
well
as a contour
that
has only zo as an interior point, are shown in Figure 10.5. We thus have
1
dz
1
dz
[ +
-3--
+
-3--
=
2"i
Res[f(zo)]·
CR Z +I c, z +I
(10.8)
The C
R integralvanishes, as usual. Along Cz. z =
ria,
with
constantc,
so
that
dz =e
ia
dr
aud
1
dz
1
0
ei'dr
,{OO
dr
C2
z3 +1 =
00
(re
i
a)3
+1 =
_e
UX
io
r
3e3ia
+1.
In
particular,
if
we choose
3a
= 2rr. we obtain
f
~
=
_i21r/3
1
00
~
=
_i
27t
/
3
I.
1c,
z3 +I
10
r
3
+I
Substituting this in Equation (10.8) gives
21Ci
(I - e
i2rr/
3)[
= 2,,;
Res[f(zO)]
=}
[=
'2 /3
Res[f(zo)],
1-
e'
71:
Onthe
other
baud,
Res[f(zO)]
= lim (z -
zo)
I
2-->20 (z -
zo)(z
-
ZI)(Z
- Z2)
I I
(zo - ZI)(ZO - Z2) (e
irr/3
- eirr)(eirr/3 _ e
i5rr/
3)
'
These last two equations yield
2"i
I
27r
[ =
1-
e
i2rr/
3
(e
irr/3
_ eirr)(eirr/3 - e
i5rr/3)
=
3,,13'

10.3
EVALUATION
OF
DEFINITE
INTEGRALS
285
Cz
•
Zz
Figure10.5
The
contour
ischosenso
that
onlyoneof the poleslies
inside.
10.3.5 Principal Value
of
an Integral
So far we have discussed only integrals of functions that have no singularities on
the contour.
Let
ns now investigate the conseqnences of the presence of singular
points on the contour. Consider the integral
1
'"
f(x)
dx,
_ooX-XQ
(10.9)
principal
value
of
an
integral
where xo is a real number and f is analytic at xo. To avoid
xo-which
causes the
integrand to
diverge-we
bypass it by indenting the contour as shown in Figure
10.6 and denoting the new contour by Cu' The contour Co is simply a semicircle
of radius
E. Forthe
contour
C
u
,
we have
(
f(z)
dz = 1
xo
- <
f(x)
dx +
1'"
f(x)
dx
+ (
f(z)
dz,
Je
u
z- XQ
-00
x - XQ
xo+€
X - XQ
leo
z- XQ
In the limit E
~
0, the sum of the first two terms on the
RHS-when
it
exists-
defines the
principal
value
of
the integral in Equation (10.9):
1
'"
f(x)
.
[1
xo
- <
f(x)
1'"
f(x)
]
P
--dx=lim
--dx+
--dx.
-00
x - XQ
E~O
-00
X - XQ xo+€ X - XQ
The integral over the semicircle is calcnlated by noting that z -
Xo
= .e;e and
dz =
iee"
dO:
JeD
f(z)
dz/(z
- xo) =-i:n:f(xo). Therefore,
1
f(z)
1'"
f(x)
.
--
dz = P
--
dx -
mf(xo)·
CuZ-XQ
_ooX-XQ
(10.10)

286
10.
CALCULUS
OF
RESIDUES
Xo-E
. Figure 10.6 The
contour
Cu avoids
xo.
XO+E
Cu
(10.11)
On the other hand,
if
Co is taken below the siogularity on a contour Cd, say, we
obtaio
(
f(z)
dz
= P 1
00
f(x)
dx
+
irrf(xo).
Jed Z - XQ
-00
x - XQ
We see that the contour integral depends on how the siogular poiot
Xo
is avoided.
However, the priocipalvalue,
if
it exists, is unique. Tocalculate this priocipal value
we close the contourby addiog a large semicircle to it as before, assuming that the
contribution from this semicircle goes to zero by Jordan's lemma. The contours
C« and Cd are replaced by a closed contour, and the value of the iotegral will be
given by the residue theorem. We therefore have
P 1
00
f(x)
dx
=
±irrf(xo)
+2rri
fRes
[
f(Zj)
],
-00
x - XQ
j=l
Zj
- XQ
where the plus sign corresponds to placing the iofioitesimal semicircleio the UHP,
as shown io Figure 10.6, and the mious sign corresponds to the other choice.
10.3.10. Example.
Let us use the principal-value method to evaluate the integral
10
00
sinx
11
00
sinx
1=
--dx
= -
--dx.
ox
2_
00
x
It
appears
that
x = 0 is a
singular
pointof the
integrand;
in
reality,
however,
it is only a
removable
singularity,
ascanbe verifiedby the
Taylor
expansionof sinxJx.Tomakeuse
ofthe
principal-value
method,
wewrite
I=
~
1m
(1
00
e
ix
dX)
=
~
1m
(p
1
00
e
ix
dX).
2
-00
x 2
-00
x
Wenow use
Equation
(10.11) withthe small circlein the
UHP,
noting
that
there
areno
singularities fore
ix
[x
there.
Thisyields
1
00
ix
P - dx =
breeD)
= in.
-00
x
Therefore,
roo
sinx 1 1r
1
0
7 dx =
2:
Imuz
) = 2'
III

10.3
EVALUATION
OF
DEFINITE
INTEGRALS
287
x
•
Xo
I
e
____
1
-----
Figure 10.7 The
equivalent
contour
obtained
by
"stretching"
C
u
,
the
contour
of
Figure
10.6.
The principal value of an integral can be written more compactly
if
we deform
the contour
C
u
by stretching it into that shown in Figure 10.7.
For
small enough <,
such a deformation will not change the number of singularities within the infinite
closed contour. Thus, the LHS
of
Equation(10.10) will have limits of integration
-00
+ i< and
+00
+ i<.1f we change the variable of integration to
~
= z - ie,
this integral becomes
1
00
f(~
+i<)
d~
=1
00
f(~)
d~
=1
00
f(z)
dz
-00
~
+ ie -
XQ
-00
~
- XQ + ie
-00
Z - XQ +
ie'
(10.12)
where in the last step we changed the dummy integration variable backto z. Note
that since
f is assumed to be continuous at all points on the contour, f
(~
+is)
--->
f(~)
for small <. The last integral of Equation (10.12) shows that there is no
singularity on the new x-axis; we have pushed the singnlarity down to
XQ- i<.In
otherwords, we have given the singnlarityOnthe x-axis a small negative imaginary
part. We can thus rewrite Equation (10.10) as
p 1
00
f(x)
dx = irrf(xQ) +1
00
f(x)
dx. ,
-00
x - XQ
-00
x - XQ +
lE
where x is used instead of z in the last integral because we are indeed integrating
along the new x-axis-s-assumlng that no other singnlaritiesare present in the UHP.
A similar argument, this time for the LHP, introduces a minus sign for the first
term on the RHS and for the
e term in the denominator. Therefore,
p 1
00
f(x)
dx = ±irrf(xQ) +1
00
f(x)dx.,
-00
x - xo
-00
x - XQ ± lE
(10.13)
where the plus (minus) sign refers to the
UHP
(LHP). This result is sometimes
abbreviated as
1 I
-----,--.-
=
P--
dx
Of
irr~(x
- XQ).
x
-XO±ZE
x
-XD
(10.14)

E >
o.
288
10.
CALCULUS
DF
RESIDUES
10.3.11. Example. Let us use residuesto evaluatethe fuuction
I 1
00
e
ikx
dx
f(k)=-.
--.,
21n
-00
X-lf
The
integral
representation
01
the
e
(step)
lunction
Wehavetoclose the
contour
by
adding
a
large
semicircle.
Whether
we dothisintheUHP
orthe LHPis dictatedby the sign of k:
If
k > 0, we close inthe
UHP.
Thus,
1 1
eikZdz
[ e
ikz
]
f(k)
=
-.
--.
=Res
--.
21l'l C Z - IE Z - IE
z-vie
= lim
[(Z
- it:)
eik~
] =
e-
kE
-----+
1.
Z-+l€
Z - IE 10-+0
Onthe
other
hand,
if
k -c 0, we mustclose in the
LHP,
in whichthe
integrand
is
analytic.
Thus,
bythe
Cauchy-Goursat
theorem,
the
integral
vanishes.
Therefore,
wehave
f(k)
=
{I
ifk>O,
o
ifk<O.
theta(orstep) This is precisely the definition of the theta fnnction (or step function). Thus, we have
function
obtained
an
integral
representation
of
that
function:
I 1
00
e
ixt
O(x) =
-.
--.
dt.
2Jrl
-00
t - IE
..
Now
supposethat thereare two singularpointson the realaxis, atXI
and
xz.
Let
us avoid XI and Xz by making little semicircles, as before, letting both semicircles
be in the
UHP
(see Figure 10.8). Without writing the integrands, we can represent
the contour integral by
The principalvalue
of
the integral is naturallydefined to
be
the sum
of
all integrals
having
E in their limits.
The
contribution from the small semicircle
Clean
be
calculated by substituting z -
XI = Ee
ie
in the integral:
r
f(z)dz
1°
f(xI
+Eeie)iEe
ie
de
.
f(xI)
leI
(z - Xl)(Z - Xz) = x Eeie(Xl +Ee
W
- Xz) =
-In
Xl - X2'
with a similar result for
CZ.
Putting everything together, we
get
pl
OO
f(x)
d .
f(xz)-f(xI)
2 'LR
x -
l1t
= 1i1
es.
-00
(x - Xl)(X - Xz) Xz - XI
If
we inclnde the case where
both
CI and Cz are in the LHP, we
get
pl
oo
f(x)
d ±.
f(xz)-f(Xl)
+ 2 'LR
x =
tit
1!1 es,
-00
(x - XI)(X - Xz) Xz - Xl
(10.15)
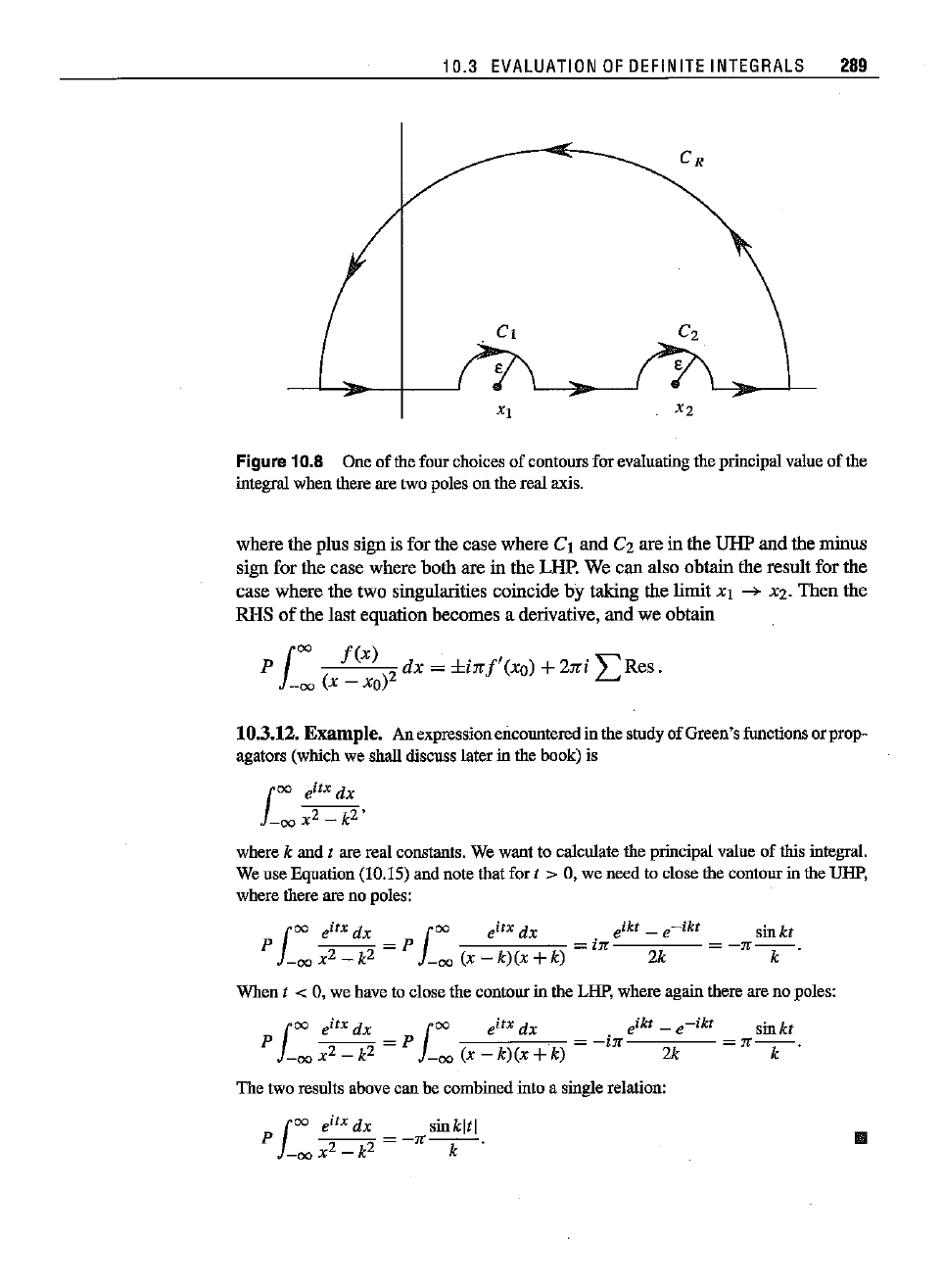
10.3
EVALUATION
OF
DEFINITE
INTEGRALS
289
XI
C2
X2
Figure10.8 One of the four choices
of
contours for evaluating
the
principal value
of
the
integral
whenthereare twopoleson the real axis.
where the plus sign is for the case where CI and C2 are in the
UHP
and the minus
sign for the case where both are in the
LHP.
We can also obtain the result for the
case where the two singularities coincide by taking the limit
Xl
-->
X2.
Then the
RHS
of
the last equation becomes a derivative, and we obtain
J
OO
f(x)
.
."
P 2
dx
=
±mf'(xo)
+
2m
L...Res.
-00
(x - xo)
10.3.12. Example. An expressionencounteredin the study
of
Green's
functions or prop-
agators (which we shall discuss later
in the book) is
1
00
eitx dx
_oox
2
- k
2
'
where k
and
t are real constants. We want to calculate
the
principal value
of
this integral.
We use Equation (10.15)
and
note
that
for t > 0, we
need
to close the contour in the UHP,
where there are no poles:
1
00
eitx dx 1
00
e
itx
dx e
ikt
-
e-
ikt
sinkt
P
---=P
=irr
--'Jr--
-00
x
2
- k
2
-00
(x -
k)(x
+k) 2k -
k·
When
t < 0, we have to close the
contour
in the LHP, where again there are no poles:
1
00
eitx
dx
1
00
e
itx
dx
e
ikt
-
e-
ikt
sin kt
P
-00
x-2---k-2 = P
-00
(x -
k)(x
+ k) =
-Ln
2k =
Jr-
k
- ·
The tworesultsabovecanbe combinedintoa singlerelation:
1
00
eitx dx
sinkltl
P
-2--2
=
-Jr--.
-oox
-k
k
11II
290 10.
CALCULUS
OF
RESIOUES
10.4 Problems
(c) J
cosz
dz:
Yc
z(z -
n)
(f)
J
I-~OSZ
dz:
Yc
z
(")
J dz
I
Yc
Z3(Z +
5)'
i:
(I)
zdz.
cZ
J
4z-3
(a)
Yc
z(z _ 2) dz.
i
2+1
(d) z dz:
c z(z - I)
()
i
sinh z
g
-4-
dz
.
c z
(j)
i
tanzdz
.:
i
dz
(m)
-.--
c z2
s
in Z'
10.1. Evaluate each of the following integrals, for all of which C is the circle
lel
= 3. I
!
i
eli
(b) i dz:
c z(z i
in)
i
cosh
z
(e)
2
-I-
2 dz:
c z n
(h) izcos
(D
dz.
J dz
(k)
Yc
sinh
2z'
i
e'dz
(n) .
C (z -
I)(z
- 2)
10.2.
Leth(z)
be analytic and have asimple zero at z = zo. and let g(z) be analytic
there. Let
!(z)
=
g(z)/
h(z), and show that
g(zo)
Res[!(zo)]
=
h'(zo)'
10.3. Find the residne of
!(z)
=
1/
cos z at each of its poles.
10.4. Evaluate the integral J:'
dx/[(x
2
+
l)(x
2
+4)] by closing the contour (a)
in the UHP and
(b) in the LHP.
10.5. Evaluate the following integrals, in which a and b are nonzero real constants.
R+ib
-R
o
10.4
PROBLEMS
291
R+ib
-
+R
where a
;f
±1.
where a
;f
±1.
(b)
{2"
d8 where a > 1.
io
a+cos8
10
2;< d8
(d)
where a, b >
O.
o (a
+bcos
2
8)2
(f)
("
d¢ where a
;f
±1.
io
1-
Zacos ¢
+a
2
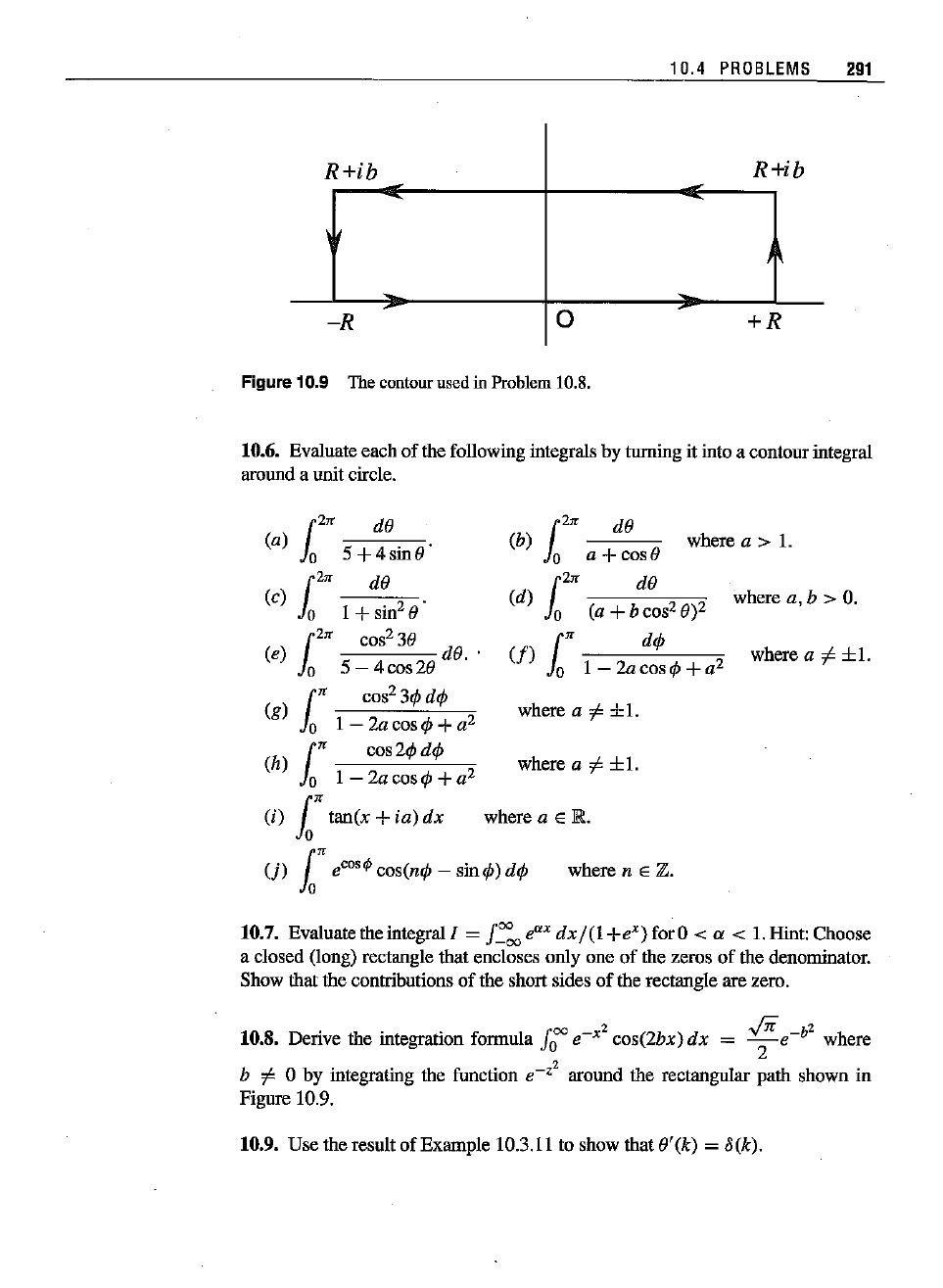
Fi9ure 10.9 The
contour
usedin
Problem
10.8.
10.6. Evaluate each of the following integrals by turning it into a contour integral
around a unit circle.
(2" d8
(a)
io
5+4sin8
10
2"
ae
(e)
o
l+sin
28'
10
2" cos238
(e)
ao
..
o
5-4cosZ8
t"
cos
2
3¢
d¢
(g) i
o
1-
Zacos¢
+ a
2
(h)
["
cos Z¢
d¢
io
1 - Zacos¢ + a
2
(i)
10"
tan(x + ia)
dx
where a E R.
(j)
10"
e
Cos
~
cos(n¢ - sin
¢)
d¢ where n E Z.
10.7. Evaluate the integral I =
f'''ooeuxdx/(I+eX)forO
< a < 1.
Hint
Choose
a closed (long) rectangle that encloses only one of the zeros of the denominator.
Show that the contributions of the short sides
of
the rectangle are zero.
10.8. Derive the integration formnla
f
o
oo
e-
x2
cos(Zbx)dx
=
V;
e-
b2
where
b
;f
0 by integrating the function
e-
z2
around the rectangnlar path shown in
Figure 10.9.
10.9. Use the result of Example 10.3.11 to show that
8'(k)
= 8(k).

292
10.
CALCULUS
OF
RESIDUES
10.10. Find the principal values
of
the following iutegrals.
(d)
1
00
sinxdx
(a) .
-00
(x
2
+4)(x - I)
1
00
x cosx
(c) 2 5
dx.
-oox
-
x+6
10.11. Evaluate the following integrals.
1
00
cosax
(b)
--dx
-00
I
+x
3
1
00
l-cosx
2
dx.
-00
x
where a "':O.
(d)
(f)
rOO
xl
_ b
2
(Sin
ax)
(a) Jo x2 +b2
-x-
dx.
1
00
sin ax
(c) dx
o
x(x
2
+b
2)2
.
1
00
8in2 x
dx
(e)
o x
2
'
Additional Reading
(b)
roo
sin ax d
Jo
x(x
2
+b2) x.
1
00
cos 2ax - cos 2bx d
2 x.
o x
roo
sin
3
x dx
10
x
3
·
I. Dennery, P.and Krzywicki, A. Mathematics for Physicists, Harper and Row,
1967. Includes a detailed discussion
of
complex analysis encompassing ap-
plications
of
conformal mappings and the residue theorem to physicalprob-
lems.
2. Mathews, J. and Walker, R. Mathematical Methods
of
Physics, 2nd ed.,
Benjamin, 1970. A "practical" guide to mathematical physics, including a
long discussion
of
"how to evaluate integrals" and the use of the residue
theorem.
