Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


10.2 CLASSIFICATION
OF
ISOLATED
SINGULARITIES 273
Thisgives
Res[!(z,)]
=3. Similarly, expandingaroundz = I gives
2z-3
= 3
__
I_=
__
I_+
3I:(_I)n(Z_I)n,
z(z - I) z - I + I z - I z - I
k=O
whichyields
Res[!(z2)]
=
-I.
Thus,
1.
2z - 3 dz =
2"iIRes[!(z,)]
+
Res[f(Z2)]}
=
2"i(3
- I) =
4"i.
Yc
z(z - I)
10.2 Classification
of
Isolated Singularities
III
Let [ : iC
->
iChave an isolated singularity at
zoo
Then there exist a real number
r > 0 and an annular region 0 < [z-
zol
< r such that Tcan be represented by
the
Laurent
series
(10.3)
principal
partofa
function
removable
singular
point
poles
defined
simple
pole
essential
singularity
The second sum in Equation (10.3), involving negative powers
of
(z - zo), is
called the
principal
part
of
[ at
zoo
We can use the ptincipal part to distinguish
three types
of
isolated singularities. The behavior
of
the function nearthe isolated
singularity is fundamentally different in each case.
I.
If
b
n
= 0 for all n 2: I,
zo
is called a
removable
singular
point
of
f .In
this case, the Laurent series contains only nonnegative powers
of
(z - zo),
and setting
[(zo) =
ao
makes the function analytic at
zoo
For example, the
function
fez) =(e' - 1 -
Z)/z2,
which
is indeterminate at z =0, becomes
entireif we set
[(0)
=1,becauseits Lanrentseries fez) =
~+~+
:~
+...
hasno
negative
power.
2.
If
b
n
= 0 for all n > m and b
m
# 0, zn is called a
pole
of
order
m. In this
case, the expansion takes the form
~
n bi »:
[(z)
=
L..,
an(z - zn) +
--
+...+-:---=-:-:::-
n~O
Z -
zo
(z - zo)"
for 0 <
lz
- zn] < r. Inparticular, if m = 1,
ZO
is called a
simple
pole.
3.
If
the principal part
of
[ at
zo
has an infinite number
of
nonzero terms, the
point
zo
is called an essential
singularity.
A prototype
of
functions that
have essential singularities is

274 10. CALCULUSOFRESIOUES
which has an essential singularity at z = a
and
a residue
of
I there. To see
how
strange
such
functions
are,
we let a be anyreal
number,
and
consider
z =
I/Ona
+
2n,,0
for n =0,
±1,
±2,
....
For such a z we have e
1
/
z
=
elna+2mri =
ae
2nni
=
a.
In
particular,
asn
---+
00,
Zgets
arbitrarily
closeto
the origin. Thus, in an arbitrarily small neighborhood
of
the origin, thereare
infinitely many points at which the function
exp(l/z)
takes on an arbitrary
value
a. In other words, as z
--->
0, the function gets arbitrarily close to any
real number! This result holds for all functions with essential singularities.
10.2.1.
Example.
ORDER OF POLES
(a) The function(zz - 3z
+5)/(z
- I) hasa Laurentseriesaroundz = I containingonly
1hreetenns:
(zZ
-3z+5)/(z
-I)
=
-I
+
(z-I)+3/(z
-I).
Thus,ithas a simplepole
atz = 1,witha residue of 3.
(b) Thefunction
sinz/z
6
has aLaurentseries
sinz 1
00
z2n+l
1
lIz
7 = z6
~(_I)n
(2n +
1)1
= z5 - 6z
3
+ (5!)z -
7!
+ ...
about
z =
O.
The
principal
part
has
three
terms.
Thepole, atz = 0, is of
order
5,
and
the
functionhas a residueof 1/120 at z =
O.
(c) The function
(zZ
- 5z +
6)/(z
- 2) has aremovahle singularityat z =2, because
zZ
- 5z
+6
= (z - 2)(z - 3) = z _ 3 =
-I
+ (z
-2)
z-2 z-2
andb
n
= afor all n.
III
10.2.2.
Example.
SINGULARITIES
OF A RATIONAL FUNCTION
rational
function
In this
example
we show
that
a
function
whose only
singularities
in the
entire
complex
plane
arepolesmusthe a rationalfunction,
1
i.e., the
ratio
of two
polynomials.
Letf be
sucha
function
and
let{zj
lJ=l
beitspolessuch
that
Zj isof
order
ml :
Expand
the
function
about
zt in a
Laurent
series
A
function
whose
only
singularities
in
the
entire
complex
plane
are
poles
isa
rational
function.
bj
b
mj
~
k
Pt(z)
fez)
=
--
+...+ ( )mj +
L"
ak(Z - Zt)
==
( )mj + 81(Z),
Z - Zl Z - Zl k=O Z - Zl
where
Pj
(z) is a polynomialof degree
mj
- I in z and 81 is analytic at
Zj.
It should be
clear
that
the
remaining
polesof f
are
in
gl.
So,
expand
gl
about
Z2 in a
Laurent
series.
A similar argumentas aboveyields81(z) = Pz(z)/(z - Zz)m
2
+
8Z(Z)
where P2(Z)is a
polynomial
of
degree
m2
- Iin zandg2 is
analytic
atzt
and
Z2.
Continuing
inthis
manner,
we get
where
g hasnopoles.Sinceallpolesof f havebeenisolatedinthesum,g mustbe
analytic
everywhere
in C, i.e., an
entire
function.
Now
substitute
1/t forz,
take
thelimitt --+ 0,
lWe
assume
that
thepointat
infinity
is nota poleof the
function,
i.e., that
f(l/z)
doesnothaveapoleatthe
origin.

10.3
EVALUATION
OF
DEFINITE
INTEGRALS
275
andnote
that,
sincethedegreeof Pi is mi - 1, all the
terms
in the
preceding
equation
go
to zeroexceptpossibly
gO/t).
Moreover,
lim
g(l/t)
i'
00,
HO
because, by
assumption,
thepointat
infinity
is nota pole of
f.
Thus,g is a
bounded
entire
function.
By
Proposition
9.5.5, g mustbea
constant.
Taking
a
common
denominator
forall
thetermsyieldsa ratioof two polynomials. II
The
type
of
isolated singularity that is most importantin applications is
of
the
second
type-poles.
For
a function thathas a pole
of
orderm at zo, the calculation
of
residaes is routine. Such a calculation, in turn, enables us to evaluate many
integrals effortlessly. How do we calculate the residue
of
a function f having a
pole
of
orderm at zo?
It
is clear that
if
f has a
pole
of
order m, then g :
iC
-->
iC
defined by
g(z) es (z - zo)m
f(z)
is analytic at
zoo
Thus, for any simple closed contour C that
contains
zo
but no other singular point
of
f,
we have
Iii
i
g(z)dz'
g(m-l)(zo)
Res[f(zo)]
=
-2'
f(z)dz
=
-2'
( )m = (
1)1'
1l'1 C
7n
C z - zo m - .
Interms
of
f this yields
2
I d
m
-
I
Res[f(zo)]
= (
1)1
lim
d ..
-I
[(z -
zo)"
f(z)].
m - .
z-e-zn
Z
For the special, but important, case
of
a simple pole, we obtain
Res[f(zo)]
= lim [(z -
zo)f(z)].
Z--+ZQ
10.3 Evaluationof DefiniteIntegrals
(lOA)
(10.5)
The
mostwidespreadapplication
of
residuesoccursin the evaluation
of
realdefinite
integrals.
It
is possible to "complexify" certain real definite integrals and relate
them to contour integrations in the complex plane. We will discuss this method
shortly; however, we first need a lemma.
10.3.1. Lemma. (Jordan'slemma)
Let
CR be a semicircle
of
radius R in the upper
half
of
the complex plane (UHP)
and
centered at the origin.
Let
f be afunction
that tends uniformly to zerofaster than
l!I'zl for arg(z) E [0,
n]
as [z] -->
00.
Let
0: be a nonnegative real number. Then
2Thelimitis
taken
becauseinmanycasesthemere
substitution
of zomayresultinan
indeterminate
form.

276
10.
CALCULUS
DF
RESIDUES
Proof. For Z E CR we write z = Re
i9,
dz = IRe
i9
de, and
IOIZ
= IOI(Rcos e +
IR
sin e) =
IOIR
cos e -
OIR
sine
and substitute in the absolute value
of
the integral to show that
IIRI
:s1o"
e-·Rsin9
Rlf(Re
i9)lde.
By assumption,
Rlf(Re
i9
)1<
feR)
independent
of
e, where
feR)
is an arbitrary
positive number that tends to zero as
R
--->
00.
By breaking up the interval of
integration into two
equal
pieces andchanging eto n - ein the second integral,
one can show that
IIRI <
2f(R)
10,,/2
e-·
Rsin9de.
Furthermore, sine
"=
2eIn for 0
:s
e
:S
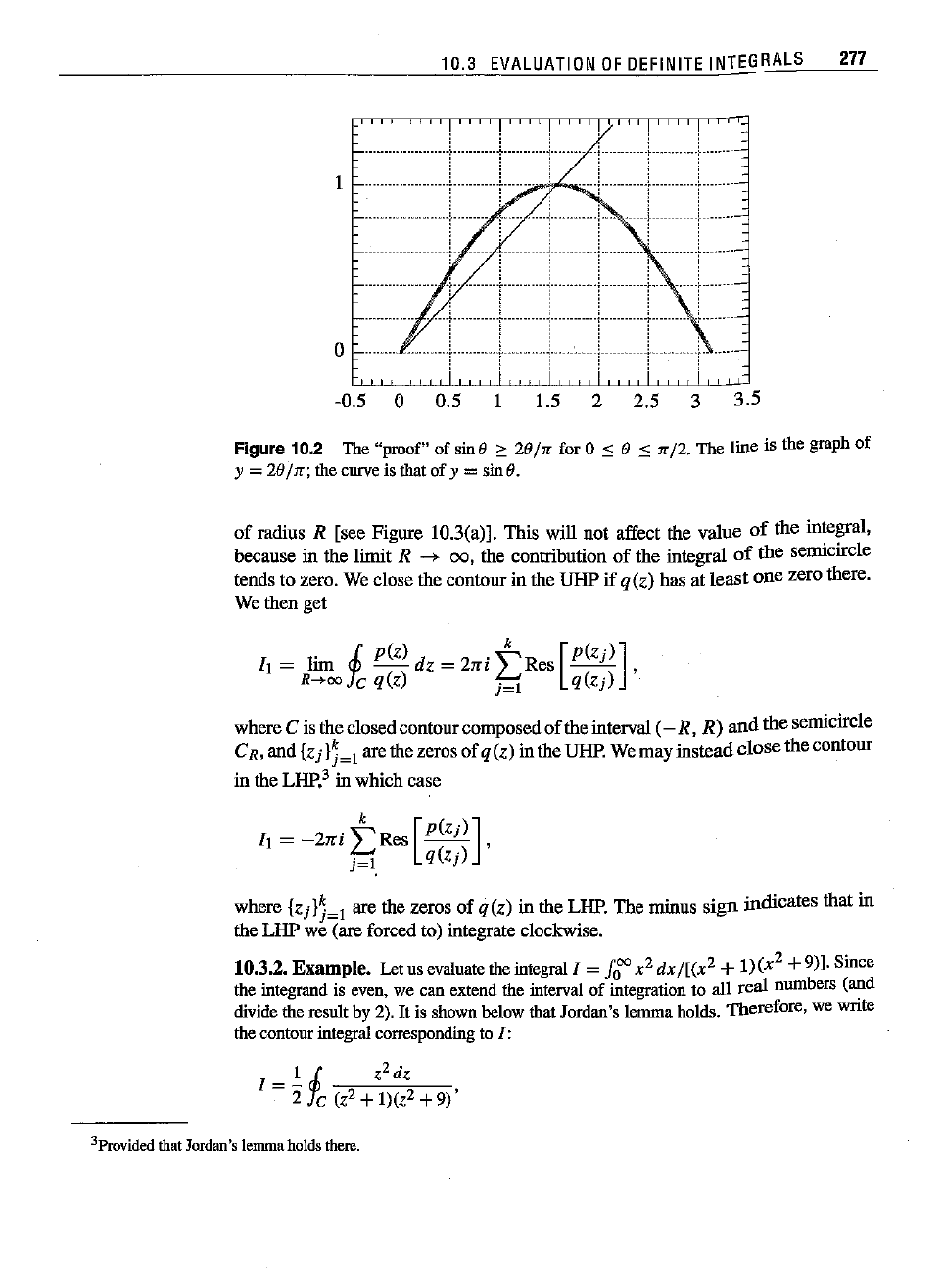
n12 (see Figure 10.2 for a "proof").
Thus,
fo
"f2 .
nf(R)
Ihl
<
2f(R)
e-(2.R/,,)9de =
--(I
-
e-·
R),
o
OIR
which goes to zero as R gets larger and larger.
D
Note that Jordan'slemmaapplies
fora
= 0 aswell, because
(I-e-·
R)
--->
OIR
as a
--->
O.
If
a < 0, the lemma is still valid
if
the semicircle CR is taken in
the lower half of the complex plane (LHP) and
fez)
goes to zero mtiformly for
n
:S
arg(z)
:S
2n.
We are now in a position to apply the residue theorem to the evaluation of
definite integrals. The three types of integrals most commonly encountered are
discussed separately below.
In all cases we assume that Jordan's lemma holds.
10.3.1 Integrals of Rational Functions
The first type of integral we can evaluate using the residue theorem is of the form
I
-100
p(x)
d
1-
--
x
-00
q(x)
,
where
p(x)
and
q(x)
are real polynomials, and
q(x)
f=
0 for any real x. We can
then write
t, =
lim
1
R
p(x)
dx = lim r
p(z)
dz
R....
oo
-R
q(x)
R....
oo
lex
q(z)
,
where Cx is the (open) contour lying on the real axis from - R to +R. Assuming
thatJordan's lemmaholds, we can close that coutourby adding to it the semicircle
10.3 EVALUATION DFDEFINITEINTEGRALS 277
----------r--------
A ---+-------!----------'\.
----r-··.--
1/,,-
.i.,
-+.--------.
!--------~---'\i,--------
-!
....
__
...
i···········-r-·········-t·
__
······_+·····--T
.........
i···········_j_···········f··
_·_·-t-·_---------:--·_···_----+----
·····1
I
o
-0.5 0 0.5
I 1.5 2 2.5 3
3.5
Figure 10.2 The"proof" of sin6 :::
26/"
for
0",
6
'"
"/2.
The line is the graphof
y =
26/,,;
thecurve is thatof y = sin6.
of
radius R [see Figure lO.3(a)]. This will not affect the value
of
the integral,
because in the limit
R
--+
00,
the contribution
of
the integral
of
the
semicircle
tends to zero. We close the contour in the
UHP
if
q(z)
has at
least
one
zero there.
We then get
!J = lim
J:
p(z)
dz =
2"j
~Res
[P(Zj)]
R-+C.,rCq(z)
~
q(Zj)
,
where C is the closedcontourcomposed
of
the interval (- R, R)
and
the
semicircle
C
R,and (Zj
11~t
are the zeros of q(z) in the UHP.We may instead
close
the contour
in the LHP,3 in which case
where
(Zj
I
1=1
are the zeros of
q(z)
in the LHP. The minus
sign
indicates
that in
the LHP we (are forced to) integrate clockwise.
10.3.2.
Example.
Letusevaluate the
integrall
= 1
0
00
x
2
dx/[(x
2
+
1)(x
2
+9)].Since
the
integrand
is even,we can
extend
the
interval
of
integration
to all real
numbers
(and
dividethe resultby2).
It
is shownbelowthat Jordan's lemmaholds. Therefore, we write
thecontour
integral
corresponding to I:
3Provided
that
Jordan's
lemmaholds
there.

278 10.
CALCULUS
OF
RESIDUES
where
C is as shownin
Figure
1O.3(a).
Note
that
the
contour
is
traversed
in thepositive
sense.Thisisalways
true
forthe
UHP.
The
singularities
ofthe
function
intheUHP
are
the
simple polesi and3i
corresponding
to thesimplezerosof the
denominator.
The
residues
atthesepoles
are
2 1
Res[f(i)]
= lim (z _ i) z
--
z....t (z -
i)(z
+i)(z2 +9) 16i '
Res[f(3i)]
= lim (z _ 3i) z2 = 3
z....3' (z2 +
l)(z
-
3i)(z
+3i)
16i'
Thus,we
obtain
It is
instructive
to
obtain
thesame
results
usingthe
LHP.
In thiscase,the
contour
is as
shownin
Figure
10.3(b) andis
taken
clockwise,so wehaveto
introduce
aminussign.The
singular
points
areatz =
-i
and
z = - 3i. Thesearesimplepolesatwhichthe
residues
of
the
function
are
2
Res[f(-O]
= lim (z +
O-:----::--,----,-z--,---,,---:::-
z....
-,
(z -
i)(z
+
i)(z2
+9)
16i'
2
Res[f(-3i)]
= lim (z +3i) z =
z....
-3'
(z2 +1)(z -
3i)(z
+3i)
Therefore,
3
16i
Toshow that
Jordan's
lemma
applies
to this
integral,
we have only to establish
that
limR-4oo
Rlf(Re
i8)1
=
O.
In the case at
hand,
a = 0 because
there
is no
exponential
function
inthe
integrand.
Thus,
whichclearlygoes tozeroasR --+
00.
10.3.3.
Example.
Let us uow consider a slightly more complicatedintegral:
1
00
x2dx
-00
(x
2
+
1)(x
2
+
4)2'
11II
which in the UHP turns into
Pc
z2
dz/[(z2
+
l)(z2
+4)2]. The poles in the UHP are at
z = i andz = 2i. Theformer is a simplepole, andthe
latter
is a pole of
order
2.
Thus,

10.3
EVALUATION
OF
DEFINITE
INTEGRALS
279
3i
-R
(a)
-i
-3i
(b)
R
Figure10.3 (a)Thelargesemicircleis cbosenin the
UHP.
(b) Notebowthe directionof
contour
integration
is
forced
tobeclockwisewhenthe
semicircle
is
chosen
inthe
LHP.
usingEquations(l0.5) and (10.4),we obtain
Res[f(i)l=
lim(z-i)
z2 =
__
1_,
z....i (z -
i)(z
+i)(z2 +4)2 18i
Res[f(2i)]
=
_1_
lim
.'!-
[(Z
_2i)2 z2 ]
(2 -
1)1
z....2' dz (z2+
I)(z
+ 2i)2(z - 2i)2
d [ z2 ] 5
=
,~,
dz (z2+
I)(z
+2i)2 =
72i'
and
f
oo
~~.::x_2=dx:;.-_~
_
2"i
(
__
1_
+
_5_)
_
z.
-00 (x
2+1)(x
2+4)2
- 18i 72i -
36'
Closingthe
contour
in the
LHP
wouldyieldthesame
result.
10.3.2 Products of Rational and Trigonometric Functions
III
The
second type
of
integral we can evaluate using the residue theorem is of the .
form
1
00
pIx)
--cosaxdx
-00
q(x)
or
1
00
pIx)
.
--smaxdx,
-00
q(x)
where a is a real number,
pIx)
and
q(x)
are
real polynomials in x,
and
q(x)
has
no real zeros. These integrals are the real and imaginary parts
of
I
1
00
pIx)
'ax
d
2=
--e
x.
-00
q(X)
280 10.
CALCULUS
DF
RESIDUES
The presence
of
e
iax
dictates the choice
of
the
half-plane:
If
a
"=:
0, we choose
the
UHP; otherwise, we choose
the
LHP. We must,
of
course,
have
enoughpowers
of
x in the denominatorto render
Rjp(Reie)/q(ReiB)1
uniformlyconvergent to zero.
10.3.4.
Example.
Letusevaluate
!-""oo[cos
ax/(x
2
+
IP]
dx wherea
'i
O.
Thisintegral
is the real part
of
the integral h =
J~oo
e
iax
dx
/ (x
2
+1)2.
When
a > 0, we close in the
UHP
as advised by Jordan's lemma.
Then
we
proceed
as for integrals
of
rationalfunctions.
Thus, we have
i
eiaz
h = 2 2 dz =2rri
Res[f(i)]
C (z + I)
fora>
0
because there is only one pole (of order 2) in the UHP at z = i, We next calculate the
residue:
Res[f(i)]
= lim
.'!..-
[(z
- i)2
e~az
2J
z-->i
dz
(z -
i)
(z +i)
. d [ e
iaz
J .
[CZ
+
i)iae
iaz
-
2e
iaZ
J
e-
a
= Inn -
---
=
Inn
=
-(I
+a).
z-+i dz (z +i)2
z-vt
(z +i)3 4i
Substituting this in the expression for 12. we obtain h =
Ie-a(l
+a) for a > O.
When
a < 0, we have to close the contour in the LHP, where the
pole
of
order
2 is at
z
=
-i
and
the contour is taken clockwise. Thus, we
get
i
eiaz
h = 2 2 dz =
-2rri
Res[t(-i)]
C (z +I)
For
the residue we obtain
for
a <
O.
d [ e
iaz
J e
a
Res[f(-i)]
= lim - (z +i)2 2 2 =
--(1-
a),
z-->-i dz (z -
i)
(z +i) 4i
and
the expression for h becomes h =
~ea(l
- a) for a < O.We can combine the two
results
and
write
1
00
cosax
7f I I
2 2 dx =
Re(l2)
= lz =
-(I
+
lal)e-
a .
-00
(x + I) 2
10.3.5.
Example.
As anotherexample,let us evaluate
III
1
00
x sin ax
---dx
-00
x
4
+ 4
where a
'i
O.
This is the imaginary part
of
the integral h =
J~oo
xe
iax
dx/(x
4
+4),
which, in terms
of
z and for the closed contour in
the
UHP
(when a > 0), becomes
i
zeiaz m
tx>
-4--dz=2rriLRes[f(Zj)]
C z
+4
j~l
for
a>
O. (10.6)

10.3
EVALUATION
OF
DEFINITE
INTEGRALS
281
The
singularities
are
determined
by the zeros of the
denominator:
z4 + 4 = 0, or Z =
1± i,
-1
± i, Of
these
four
simplepoles only two, 1+ i and
-1
+i, areinthe
UHP.
We
nowcalculate the
residues:
zei
az
Res[f(1 + i)] = lim (z - I - i) . . . .
z-->1+;
(z - I
-,)(z
- I +
,)(z
+
I-,)(z
+
1+,)
(1 +i)e
ia
(l+ i)
eiae-
a
(2i)(2)(2 +2i) 8i
ze
iaz
Res[f(-I
+ ill = lim (z + I - i) . . . .
z-->-1+;
(z + I
-,)(z
+ I +
,)(z
-
I-,)(z
-
1+,)
(-1
+Oi
a
(- l+ i)
e-iae-
a
(2i)(-2)(-2
+
2i)
8i
Substituting in Equatiou(10.6),we obtain
e-
a.
. x
12
=
2rci""""8i(ela
_e-
W
)
=
ize-asina.
Thus,
1
00
x sinax 1r
-4--
dx
=
lm(h)
=
_e-
a
sina
-00
x
+4
2
for
a>
O.
(10.7)
Fora < 0, we couldclose the
contour
in
the
LHP.
But
there
is aneasierwayof
getting
to
the
auswer.
Wenotethat
-a
> 0, audEquation(10.7)yields
1
00
xsinax
1
00
xsin[(-a)x]
1r
(a).
n
--dx=-
dx=--e--
sm(-a)=-easina.
-00
x
4
+ 4
-00
x
4
+ 4
2 2
Wecancollectthetwocasesin
1
00
x
sin-ax
1C
I I
---dx
=
_e-
a
sina.
-00
x
4
+ 4 2
10.3.3 Functions
of
Trigonometric Functions
The third type
of
integral we can evaluate
usingthe
residue theorem involves only
trigonometric functions and is
of
the form
fo2n
F(sinO, cos 0)
ao.
where F is some (typically rational) function
of
its arguments. Since0 varies from
oto
217:
,we can considerit an argument
of
apointz on the unitcirclecenteredat the
origin. Thenz
= e
W
and
e-
w
=
I/z,
and we can substitute cos 0 = (z +
l/z)/2,
sinO = (z -
l/z)/(2i),
and
dll
=
dz/(iz)
in the original integral, to obtain
J F
(Z
- I/z, z+I/Z)
~z.
Jc
2, 2 IZ
This integral can often be evaluated using the method of residues.

282 10.
CALCULUS
OF
RESIDUES
a
-I-~
Z2 =
and
a
10.3.6.
Example.
Let us evaluate the integral frdO/(1 +
acosO)
where
faJ
< 1.
Substituting for cos () and
de
in terms
of
z, we
obtain
1.
dz/iz
21.
dz
f
c
1+
a[(z2 + 1)/(2z)] = i
fc
2z + az
2
+
a'
where C is the unit circle centered at
the
origin.
The
singularities
of
the integrand are the
zerosofits
denominator:
-l+~
ai
=
For
lal< 1itis clearthat Z2 will lie outsidethe unitcircle C; therefore, it does not contribute
to the integral.
But
zt
lies inside, and we obtain
fc
2z +
::2
+ a =
2:n:i
Res[f(Zt)]·
The
residue
of
the simple
pole
at
zt
can be calculated:
Res[!(ZI)] = lim (z - Zl) (
~(
)
~
(_1_)
z-e-z
t a Z - zr Z - Z2 a zt - Z2
I (
a)
I
=;;
2v'I-a
2
=
2v'I-a
2'
It
followsthat
[2" dO 2 1. dz 2 ( I )
2:n:
1
0
1+{lcose=irc2z+az2+a=i'bri
2-!1-a
2
=
Jl-a
Z'
II
10.3.7.
Example.
As anotherexample, let us consider the integral
where
a>
1.
] _
{"
dO
-
10
(a + cos0)2
Since cos eis an even function
of
e.
we may write
where a > 1.
11"
dO
]-
-2:
_,,(a+cosO)2
This integration is over a complete cycle around the origin, and we can make the usual
substitution:
]=~1.
dz/iz
=~1.
zdz
.
2 f
c
[a
+ (z2 + 1)/2z]2 i
fc
(z2
+2az
+ 1)2
The denominator has the"roots
zt
=
-a
+Ja
Z
- 1
and
Z2 =
-a
-
vi
a
2
- 1, which are
both
of
order
2. The second
root
is outside the unit circle because a > 1. Also, it is easily
verified that for
all a > 1, zr is inside the unit circle. Since zt isa
pole
of
order
2, we have
Res[f(ZI)] = lim
'!...-
[(z
_ ZI)2 z ]
z-->z[
dz (z - ZI)2(z - Z2)2
-lim'!...-[
z
]_
I
-
z-e-zr
dz (z - Z2)2 - (Zl - Z2)2
Wethos
obtain]
=
~2:n:i
Res[!(ZI)] = 2:n:a
3/2'
, (a - I)
