Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


7.4
EXAMPLES
OF
CLASSICAL
ORTHOGONAL
POLYNOMIALS
183
merely areasonable argumentforit. Gauss, with whom he had severalquarrelsoverpriority.
considered rigorous proof the standard of ownership. To Legendre's credit, however,
he
was an enthusiastic supporter of his young rivals Abel and Jacobi and gave their work
considerable attentionin his writings. Especially in the theory of elliptic functions, the area
of competition with
Abel
and Jacobi, Legendre is considered more of a trailblazer than a
greatbuilder.
Hermite
wrotethat Legendre"is consideredthe founder of thetheory of elliptic
functions" and "greatly smoothed the wayfor his successors," but
Dotes
that the recognition
of the double periodicity ofthe inversefunction, which allowedthe greatprogress ofothers,
was missing from Legendre's work.
Legendre also contributed to practical efforts in science and mathematics. He and two
of his contemporaries were assigned in 1787
to a panel conducting geodetic work in co-
operation with
the
observatories at Paris and Greenwich. Four years later the same panel
members were appointed as the Academy's commissioners to undertake the measurements
and calculations necessary to determine the lengthof the standard meter. Legendre's seem-
ingly tireless skill at calculating produced large tables of the values of trigonometric
and
elliptic functions, logarithms, and solutions to various special equations.
In his famous textbookElements de geometrie (1794) he gave a simple proofthat 7r is
irrationaland conjecturedthat it is not the root of any algebraicequationof finite degree with
rational coefficients. The textbook was somewhat dogmatic in its presentation of ordinary
Euclidean thought and includes none of the non-Euclidean ideas beginning to be
fanned
aroundthat time.
It
was Legendrewho first gave a rigorous proofof the theorem (assuming
all of Euclid's postulates, of course) that the sum of the angles of a triangle
is "equal to
two right angles." Very little of his research in this area was of memorable quality. The
samecould
possibly
be arguedfor
the
balanceof his writing,botone must
acknowledge
the very fruitful ideas he left behind in number theory and elliptic functions and, of course,
the introduction of Legendre polynomials and the important
Legendre transformation used
both
in thennodynamics and Hamiltonian mechanics.
To find
k~,
we look at the evenness or oddness of the polynomials. By an
investigationof the Rodriguezformula-s-as in our study
ofHennite
polynomials-
we note that F
n(
-x)
=
(_I)n
Fn(x), which tells us that Fn(x) is either even or
odd.
In
eithercase, x will not have an (n -
l)st
power. Therefore,
k~
=
O.
We now calculate h
n
as given by (7.12):
h
n
=
(-I)nk
nn!
1
1
(l
_ x
2)ndx
=2
nr(n
+
~)/
r(~)
1
1
(1 _ x
2)ndx.
s;
-1
2
n
n! _1
The integral can be evaluated by repeated integration by parts (see Problem 7.8).
Substituting the result in the expression above yields h
n
=
2/(2n
+1).
We need ct
n
,
fin
and
Yn
for the recurrence relation:
k
n
+l 2
n
+
1r(n
+ 1
+~)
n!r(~)
2n + 1
ct
n
=
k::
= (n +
1)!r(~)
2
nr(n
+~)
= n + 1 '
where we used the relation I'(n-l- 1
+~)
=
(n+
~)r(n+
~).
We also have fin =0
(becauseej,
= 0 =
k~+I)
and Yn =
-n/(n+l).
Therefore, the recurrencerelation

184 7.
CLASSICAL
ORTHOGONAL
POLYNOMIALS
is
(n +l)Pn+I(X) = (2n +
l)xPn(x)
-nPn-I(X).
(7.20)
Now we use
K,
=
-2,
Pl(X) = x
=}
kl = 1, and 02 =
-1
to obtain
An =
-n(n
+1), which yields the following differential equation:
d [ 2
dP
n]
dx
(l-x)
dx
=
-n(n
+
l)P
n·
This can also be expressed as
2 d
2P
n
ar;
(l
- x )
dx
2
-
2x
dx
+
n(n
+
l)P
n =
O.
7.4.4 Other Classical Orthogonal Polynomials
(7.21)
(7.22)
The rest of the classical orthogonal polynomials can be constructed similarly. For
the sake of completeness, we merely quote the results.
Jacobi Polynomials,
P::'v
(x)
Standardization: K; =
(-2)nn!
Constants: k
n
=
2-n
r(2n
+
fJ.
+v +
1),
k' =
n(v
-
fJ.)
k
n!r(n
+
fJ.
+v +1) n 2n +
fJ.
+v n,
2,,+v+l
r(n
+
fJ.
+
l)r(n
+v +1)
hn =
-:-:c::-----'----'--'---=-'----'-------'----'-,.,-
n!(2n +
fJ.
+v +
l)r(n
+
fJ.
+v +1)
Rodriguez formula:
Differential Equation:
d2
P"'v
dP"'v
(1 - x
2)
__
n- +
[fJ.
- v -
(fJ.
+v +
2)x]_n_
dx
2
dx
+
n(n
+
fJ.
+v +
l)P/:'v
= 0
A Recurrence Relation:
2(n +
l)(n
+
fJ.
+v +1)(2n +
fJ.
+
v)P:-i-~
= (2n +
fJ.
+v +1)[(2n +
fJ.
+v)(2n +u. +v +
2)x
+v
2
-
fJ.2]p/:.
v
- 2(n
+
fJ.)(n
+v)(2n +
fJ.
+v +
2)P:~~

7.4
EXAMPLES
OF
CLASSICAL
ORTHOGONAL
POLYNOMIALS
185
Gegenbauer Polynomials, C;(x)
f(n
+A+
~)r(2A)
Standardization: K -
(_2)nn'-'-
__
---"'--'-..,..:-
n - .
r(n
+2A)f(A +
~)
k
_
2n
f(n
+A) ,
..jiif(n
+2A)r(A +
~)
Constants:
~,
- 0 h - --'--;c;--:-:-=-:;;:-:-,-=,-!'--
n - n!
f(A)
, ''"n - , n - n!(n +A)r(2A)r(A)
Rodriguez Formnla:
Differential Equation:
d
2e'"
.
de'"
(1 - x
2
)
-----f
- (2A+
l)x
d"
+
n(n
+
2A)e~
= 0
dx x
A Recurrence Relation:
(n +
l)e~+l
= 2(n +
A)Xe~
- (n +2A-
l)e~_l
Chebyshev Polynomials
of
the First Kind, Tn(x)
Standardization:
K =
(_I)"
(2n)!
n
2
n
n!
Constants:
Standardization:
•
(_I)n2
nn!
d
n
Rodrfguez
Formulaz Tn(x) = .
(l_x
2
)1/2_
[(l_x
2
)"- 1/2]
(2n)! dx"
2 d
2T
n
dT
n
2
Differential Equation: (1 - x )
--2
- x - +n Tn = 0
dx dx
A Recnrrence Relation: Tn+l =
2xT
n
- Tn-l
Chebyshev Polynomials
of
the Second Kind,
U«
(x)
K _ _ 1)n (2n +I)!
n-(
2
n(n+l)!
Constants:

(7.23)
186 7. CLASSICAL
ORTHOGONAL
POLYNOMIALS
Rodriguez
Formula:
U ( ) =
(_1)n2
n(n
+
1)1
(1 _ x2)- 1/2 d
n
[(1 _ x2)"+1/2]
n x (2n +I)!
dx"
2 d
2U
n
au;
Differential
Equation:
(1 - x
)-2-
-
3x-
+
n(n
+2)Un = 0
dx
dx
A Recurrence
Relation:
Un+1
=
2xU
n
-
Un-I
7.5 Expansion in Terms
of
Orthogonal Polynomials
Having studied the different classical orthogonal polynomials, we can now use
them to write an arbitrary function
f E
£'~(a,
b) as a series of these polynomials.
If
we denote a complete set
of
orthogonal (not necessarily classical) polynomials
by ICk) and the given function by
If),
we may write
00
If)
=
Lak
ICk),
k=O
where ak is found by multiplying both sides of the equation by (Cil and using the
orthogonality of the
ICk) 's:
00
(Cil
f)
=
Lad
Cil Ck) = a; (Cil Cj)
=}
k=O
This is written in function form as
(Cil
f)
aj
= .
(CilCj)
(7.24)
(7.25)
t
C~(x)f(x)w(x)
dx
a· -
",a'-:-i:--'-'
-=--.:-'--'-:-'---'---'-----
i
r-:
J;ICj(x)1
2w(x)dx
We can also "derive" the functional form of Equation (7.23) by multiplying both
ofits
sides by (xl and using the fact that
(xl
f)
=
f(x)
and
(xl
Ck) = Ck(X).
The result will be
00
f(x)
=
LakCk(X).
k=O
(7.26)
(7.27)
7.5.1.
Example.
The solution of Laplace's equation in spherically symmetricelectro-
static
problems
that
are
independent
of the
azimuthal
angleisgivenby
~(
bk k)
<I>(r,
0) =
L..
HI
+ckr
Pk(COSO).
k=O r
Consider
two
conducting
hemispheres
of
radius
a
separated
by a
small
insulating
gap
atthe
equator.
The
upper
hemisphere
is heldat
potential
Vo
andtheloweroneat-
Vo.
as
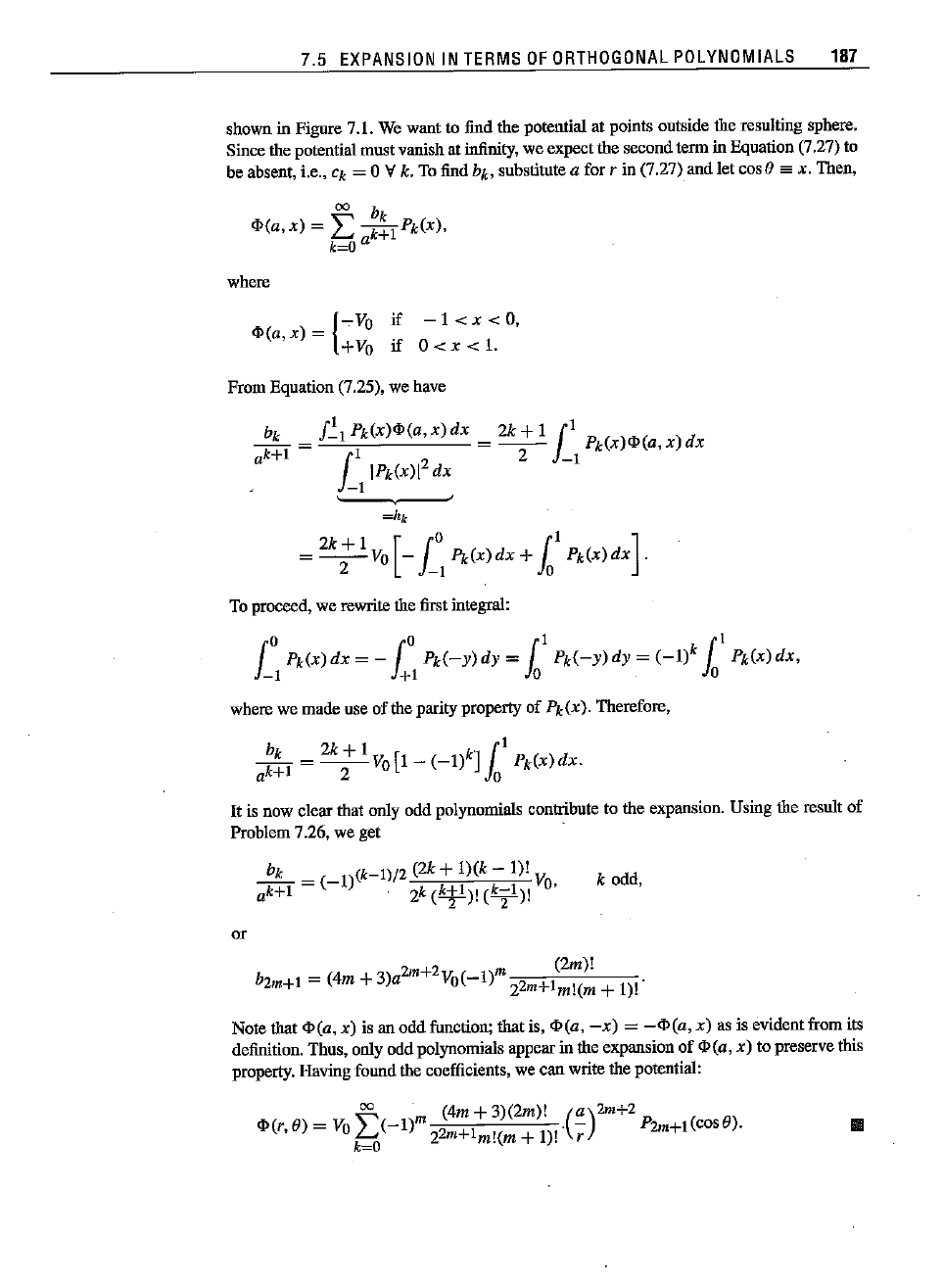
7.5
EXPANSION
IN
TERMS
OF
ORTHOGONAL
POLYNOMIALS
187
shownin
Figure
7.1. Wewantto findthepotential atpointsoutsidethe
resulting
sphere.
Sincethe
potential
mustvanishat
infinity,
we expectthesecondterm in
Equation
(7.27)to
be absent, i.e., Ck = 0 V k. To find
bb
substitute a for r in (7.27) and let cosB
'"
x. Then,
00
bk
<I>(a,
x) = L
HI
Pk(X),
k=Oa
where
{
V. if - I < x < 0,
<I>(a,
x) = - 0
+Vo
if
ue x -c L
From Equation (7.25), we have
2k +
111
-2-
Pk(X)
<I>
(a, x)
dx
-1
To
proceed,
we
rewrite
the
first
integral:
1
0
Pk(x)dx
= _
fO
Pk(-y)dy
=
f1
Pk(-y)dy
=
(_I)k
f1
Pk(x)dx,
-1 1+1
10
10
where
we madeuse oftbe
parity
property
of Pk(X).
Therefore,
bk
2k+1
k r
a
H 1
=
-2-Vo[l-
(-I)
]
10
Pk(x)dx.
Itis nowclear
that
onlyoddpolynomials
contribute
to the
expansion.
Usingthe
result
of
Problem 7.26, we get
or
Zm+2 m (2m)!
bZ
m+1
=(4m +3)a
VO(-I)
Z +1 .
2 m
ml(m
+
1)1
Note that
<I>(a,
x) is an
odd
function; that is,
<I>(a,
-x)
= -<I>(a, x) as is evidentfrom its
definition.
Thus,onlyoddpolynomials
appear
inthe
expansion
of 4>(a,x) to
preserve
this
property.
Havingfoundthecoefficients, we canwritethe
potential:
00
m(4m + 3)(2m)1
(a)zm+z
<I>(r,B)=VoL(-I)
Z +1 . - PZ
m
+1(cos
B).
k~O
2 m
ml(m
+
1)1
r
III

188 7. CLASSICAL
ORTHOGONAL
POLYNOMIALS
Figure7.1 Thevoltageis +
Vo
forthe
upper
hemisphere,
where0
:::;
B < 1T/2, orwhere
o <
cosO:::;
1. It is
-Vo
for the lower
hemisphere,
where
7C/2
< B
:::;
rr, or
where
-1
~cose
<0.
The placewhere Legendre polynomials appearmostnatnrally is, as mentioned
above, in the solntion of Laplace'seqnationin spherical coordinates. After the par-
tial differential equation is transformed into three ordinary differential equations
using the method
of
the separation of variables, the differential equation corre-
sponding to the polar angle
egives rise to solutions of which Legendre polynonti-
als are special cases. This differential equation simplifies to Legendre differential
equation if the substitution
x = cos eis made; in that case, the solutions will
be Legendre polynontials in
x, or in cos
e.
That is why the argument of Pk(X) is
restricted to the interval
[-I,
+
I].
7.5.2.Example. Wecanexpandthe Diracdeltafunctionin tenus of Legendre
polyno-
mials.Wewrite
00
8(x) = L a"P,,(x),
n=O
where
2n+11
1
2n+1
an =
--
P
n(x)8(x)
dx =
--Pn(O).
2
-1
2
Foroddn thiswillgivezero,
because
P
n
(x)
is an oddpolynomial. To
evaluate
P
n
(0) for
even
n, we usethe
recurrence
relation(7.20)forx = 0:
n-I
or nPn(O) =
-en
-1)P,,_z(O),
or
P,,(O)
=
---Pn-z(O).
Iteratingthis m times,we
n
obtain
R 0 _ I m (n - I)(n -
3)···
(n - 2m + I)
,,( ) -
(-)
n(n - 2)(n - 4)
...
(n - 2m +2) P,,-Zm(O).
(2m - 1)(2m - 3)
..
·3'
I
Forn = 2m, thisyieldsPZ
m
(0) =
(_i)m
PoCO).
Nowwe
"fill
2m(2m - 2)
..
·4·
2
the
gaps"
in the
numerator
by multiplying
it-and
the
denominator,
of course-by the

(7.28)
7.6
GENERATING
FUNCTIONS
189
denominator.
This
yields
2m(2m
-1)(2m
-
2)·
..
3·2·1
P2m
(0) =
(_I)m
[2m(2m _ 2)
...
4 . 2]2
m (2m)! m (2m)!
=
(-I)
[2
mm!]2
=
(-I)
2
2m(m!)2'
because
Po(x)
= 1.
Thus,
we can
write
~
4m +I m (2m)!
~(x)
=
L.-
--(-I)
2 2P2m(x).
m=O
2 2 m(m!)
Wecan also
derive
this
expansion
as follows.Forany
complete
set of orthonormal
vectors
[IA}}~t,
wehave
~(x
-
x')
=
w(x)
(xl
x')
=
w(x)
(xI1Ix
')
=
w(x)
{xl
(~llk)
(AI)
Ix'} =
w(x)
~
Ik(x')lk(X).
Legendre polynomials arenotorthonormal; hutwecanmakethemsobydividing Pk(x) by
h~/2
=
..j2/(2k
+I). Then,notingthat
w(x)
= I, we obtain
,
00
Pk(X') Pk(X)
00
2k +I ,
~(x
-
x)
=
~
..j2((2k+I)
..j2(2k
+I) =
~
-2-Pk(x
)Pk(X).
For
x'
= 0 we get
~(x)
=
E~o
2k;
11'k(O)Pk(X), which agrees with the previons
result.
III
7.6 Generating Functions
It
is possible to generate all orthogonalpolynomials of a certainkindfrom a single
function of two variables
g(x,
t) by repeated differentiation of thatfunction. Such
generating
function
a function is called a
generating
function. This generating function is assumed
to be expandable in the form
00
g(x,
t) =
I>ntn
Fn(x),
n=O
so that the nth derivative
of
g(x,
t) with respect to t evaluated at t = 0 gives Fn(x)
to withina multiplicative constant. The constant anis introducedfor convenience.
Clearly, for
g(x, t) to be useful, it must be in closed form. The derivation of such
a function for general
Fn(x) is nontrivial, and we shall not attempt to derive such
a general generating
function-as
we did, for instance, for the general Rodriguez
formula. Instead, we simply quote these functions
in Table 7.2, and leave the
derivation of the generating functions of Hermite and Legendre polynomials as
Problems 7.14 and 7.20.
For
the derivation
of
Laguerre generating function, see
[Hassani, 2000] pp. 606-607.

190 7.
CLASSICAL
ORTHOGONAL
POLYNOMIALS
Polynomial Generating function an
Hermite, Hn(x)
exp(-t
2
+
2xt)
lin!
Lagnerre,L~(x)
exp[-xtl(l-t)]/(l-t)v+l
I
Chebyshev (1st kind), Tn(x) (I - t
2
)(t
2 -
2xt
+
1)-1
2, n
f=
0
ao
= 1
Chebyshev (2nd kind),
Un
(x)
(t
2
-
2xt
+1)-1
1
.\
Table
72
Generating functionsfor selectedpolynomials
7.7 Problems
7.1. Let n = 1 in Eqnation (7.1) and solve for s
dw
. Now snbstitute this in the
dx
derivative of ws
n
P,k
and show that the derivative is
eqnalto
ws
n-
l
P,k+!.
Repeat
this process
m times to prove Lennna7.1.2.
7.2. Find
w(x),
a, and b for the case
of
the classical orthogonal polynomials in
which
s(x) is of second degree.
7.3. Integrate by parts twice and nse Lennna 7.1.2 to show that
l
b
Fm(wsF~)'
dx
=0
for m < n.
7.4. (a) Using Lemma 7.1.2 conclnde that
(wsF~)'
[u: is a polynomial of degree
less than or equal to
n.
(b) Write
(ws
F~)'
Iw
as a linearcombination of F,
(x),
and use their orthogonality
and Problem 7.3 to show that the linear combination collapses to a single term.
(c)Multiplybothsides
of
the differential equation so obtainedby F
n
and integrate.
The RHS becomes hnA
n.
For the LHS, carry out the differentiation and note that
(ws)'
I w =
Kl
Fl. Now show that K1Fl
F~
+sF;:is a polynomial
of
degree n, and
that the LHS of the differential equation yields
{(Klkln
+02n(n - I)}h
n.
Now
find An.
7.5. Derive the recurrence relation of Equation (7.8). Hint: Differentiate Equation
(7.5) and substitute for
F;:
from the differential equation. Now multiply the result-
ing equation by
anx
+
fJn
and substitute for (anx +
fJn)F~
from one of the earlier
recurrence
relations.

ifn=2m.
ifn
is
odd,
7.7
PROBLEMS
191
7.6. Using only the orthogonality
of
Hermite polynomials
i:
e-X'Hm(x)Hn(x)dx
=
.j1iZ
nn!8
mn
(and the fact that they are polynomials) generate the first three
of
them.
7.7. Show that for Legendre polynomials, k
n
=
Znr(n
+
!)/[n!r(~)].
Hint:
Multiply and divide the expression given in the
book
by n!; take a factor
of
Zout
of
allterms in the nmnerator; the even terms yield a factor
of
n!, and the odd terms
give a gannna function.
7.8. Using integration by parts several times, show that
1
1(1 _
x2)"dx
= zmn(n -
I)···
(n - m +I)
II
x2m(l
_ x2)n-mdx.
-I
. 3 . 5 .7
...
(Zm - 1)
-I
Now show that
I~I
(1 - x
2)ndx
=
Zr(!)n!/[(Zn
+
1)r(n
+
!)].
7.9. Use the generalizedRodriguez formulafor Hermite polynomials and integra-
tion by parts to expand
x
2k
and x
2k
+I in terms
of
Hermite polynomials.
7.10. Use the recurrence relation for Hermite polynomials to show that
1
00
,
-00
xe-
x
Hm(x)Hn(x)dx
=
.j1i2
n-
In!
[8
m
•
n
- 1 +2(n +1)8
m
•
n
+l
]'
Whathappens when m = n?
7.11. Apply the general forma1ism
of
the recurrence relations given in the
book
to Hermite polynomials to find the following:
H
n
+
H~_I
-
2xH
n
_ 1 =
O.
7.12. Show that
1':"00
x
2e-
x
'
H;(x)
dx =
.j1i
2
n(n
+
!)n!
7.13. Use a recurrence relations for Hermite polynomials to show that
Hn(O)
=
{O
(_I)m
(2~)!
7.14. Differentiate the expansion
of
g(x, t) for Hermite polynomials with respect
to
x (treating t as a constant) and choose an such that nan =
an-I
to obtain
a differential equation for g. Solve this differential equation. To determine the
"constant"
of
integrationuse
the
result
of
Problem7.13 to showthatg(O, t) =
e-/'.

192 7.
CLASSICAL
ORTHOGONAL
POLYNOMIALS
7.15. Use the expansion of the generating function for Hermite polynontials to
obtain
Then integrate both sides over x and use the orthogonality
of
the Herntite polyno-
ntials to get
00
(sz)"
fOO
2
L:
-,-Z
e-
X
H;(x)dx
=
./iie
Z".
n~O
(n.)
-00
Deduce from this the normalization constant h
n
of
H
n
(x).
7.16. Using the recurrence relation of Equation (7.14) repeatedly, show that
f
OO
k
_x
2
{O
X e Hm(x)Hm+n(x)dx = rz:
-00
'171: 2
m
(m
+k)!
if
n > k,
if
n = k.
7.17. Given that Po(x) = I and PI (x) =x,
(a) use (7.20) repeatedly to show that
Pn(l)
= 1.
(b) Using the same equation, find Pz(x), P3(X), and P4(X).
7.18. Apply the general formalism
of
the recurrence relations given in the book
to find the following two relations for Legendre polynontials:
, ,
(a)
nP
n
-
xP; +P
n-
1
=
O.
(b)
(I
-
xZ)P~
-
nPn-l
+
nXP
n
=
O.
7.19. Show that
J~l
x
n
Pn(x)
dx
= 2
n+
1(n!)z
j(2n
+I)!. Hint: Use the definition
of
h
n
and k
n
and the fact that P
n
is orthogonal to any polynontial of degree lower
thann.
7.20. Differentiatethe expansion
of
g(x,
t)
for Legendrepolynontials, and choose
Un = I. For
P~,
you will substitute two different expressions to get two equations.
First use Equation (7.11) with
n +I replaced by n, to obtain
d
00
(I -
tZ)~
+tg
= 2
L:nt
n
Pn-l
+2t.
dx n=2
As an alternative, use Equation (7.10) to substilnte for
P~
and get
dg
00
(I-xt)-
=
L:ntnPn_l
+t.
dx
n=Z
Combinethe last two equations to get (lz -
2xt
+
I)g'
= tg. Solve this differential
equation and detemtine the constant
of
integration by evaluating g(x, 0).
