Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations

Подождите немного. Документ загружается.

8.2

THE

FOURIER

TRANSFORM

213

As in the case of Fourier series, Equations (8.20) and (8.21) are valid even

and!

are piecewise continuous.

that case the Fourier transforms are written

![f(x

+0) +

f(x

- 0)] = ~ 1

!(k)eikxdk,

'1271:

-00

![!(k+O)+!(k-O)]

~1°O

f(x)e-ikxdx,

'1271:

-00

(8.22)

where each zero on the LHS is an E that has gone to its limit.

is useful to generalize Fourier transform equations to more than one dimen-

sion. The generalization is straightforward:

1 f

'k-

f(r)

= dnke' -r

f(k)

(271:)n/2

I f 'k

!(k)

dnxf(r)e-'

.r.

(271:

)n/2

(8.23)

Let us now use the abstract notation

Chapter 6 to get more insight into the

preceding results.

the language of Chapter 6, Equation (8.20) can be written as

(8.24)

(8.25)

where we have defined

I 'k

(xlk)

=e'

'1271:

Equation (8.24) suggests the identification

If)

as well as the identity

1 =

Ik) (kl dk,

which is the same as (6.1). Equation (6.3) yields

(kl k') = 8(k - k'),

(8.26)

(8.27)

which upon the insertion

a unit operator gives an integral representation of the

delta function:

8(k - k

(klllk

') =(kl

(L:

Ix) (xl

dX)

Ik')

I 1

= (kl x)

(xl

k')

= - dxei(k'-k)x.

-00

21f

-co

Obviously, we can also write

8(x

x')

= [1/(271:)]

J":'oo

dkei(x-x'lk.

214 8.

FOURIER

ANALYSIS

than

one

dimension

involved,

weuse

8(k -

k')

_1_

fdnxei(k-k'j.r

(211")n

8(r

r')

_1_

dnkei(r-r'j.k

(211")n

with the inner product relations

(8.28)

(

k) I

rk-r

r =

(211")n/2

e ,

-ik.r

{k] r) =

(211")n/2

e •

(8.29)

Equations (8.28) and (8.29) and the identification

If)

exhibit a striking

resemblance between [r) and [k), In fact, any given abstract vector

If)

can be

expressed either in terms

its r representation, (r]

f(r),

or in terms of

its

k representation,

(kl

f(k).

These two representations are completely

equivalent, and there is a one-to-one correspondence between the two, given by

Equation (8.23). The representation that is used in practice is dictated by the

physical application.

In quantum mechartics, for instance, most of the time the r

representation, corresponding to the position, is used, because then the operator

equations turn into differential equations that are normally linear and easier to

solve than the corresponding equations in the

k representation, which is related to

the momentum.

8.2.3. Example. Inthis

example

evaluate

the

Fourier

transform

the

Coulomb

poten-

tialVCr) of a point

charge

q: VCr) =

«tr-

The

Fouriertransfonn

is importantin

scattering

experiments

with

atoms,

molecules,andsolids.As we shallseeinthefollowing, the

Fourier

Yukawa

potential

transform of V

(r)

isnot

defined.

However,

if we

work

withtheYukawapotential,

qe-

Va(r)

--,

the

Fourier

transform will be well-defined,andwe cantakethelimita

0 torecoverthe

Coulomb

potential.

Thus,

we seekthe

Fourier

transformof Va(r).

Weare

working

inthreedimensionsand

therefore

may write

Iff

-ar

Va(k)

d3xe-ik.r~.

(211")3/2

It is clear

from

the

presence

of r

that

spherical

coordinates

are

appropriate.

are

free

topickany

direction

asthez-axis.A simplifying choicein thiscaseis the

direction

of k.

So, we let k =

Iklez

=kez, or k . r =kr cos

whereeis the polar anglein spherical

coordinates.

Nowwehave

Va(k)

roo

2dr

{1C

sln sse

{21r

dcpe-ikrcos(Je-ar.

(211")3/2

10 10 10

The

integration

trivial

and

gives

217'.

The0

integration

isdone

{1C

sinOe-ikrcos(J dO =

e-ikrudu

~(eikr

e-ikr).

-'-1

ikr

8.2

THE

FOURIER

TRANSFORM

215

We thus have

Va(k) =

q(2n)

rX!

drrze-ar

_1_

Ci kr

ikr)

(211:)3/2

ikr

[00

dr [e(-a+iklr _

e-(a+ik)rj

(211:)1/2

q I

(e(-a+ik)r

e-(a+ik)r 1

)

(211:)1/2

-a

+ik 0 + ,,+

0 .

Notehowthe

factor

has

tamed

the

divergent

behavior

of the

exponential

atr

00.

This was the

reason

for

introducing

it in the

first

place. Simplifyingthelast

expression

yields Va(k) =

(2ql../'iii)(~

~)-1.

The

parameter"

is a measure of the range of the

potential.

Itis clear

that

the

larger

is, thesmallerthe

range.

In fact,itwasin

response

the

short

range

nuclear

forces

that

Yukawa

introduced

For

electromagnetism,

where

the

range

infinite,

becomes

zeroandVa(r)

reduces

toV(r).

Thus,

the

Fourier

transform

of the

Coulomb

potential

_ 2q I

VCoul

(k)

= ../'iiik2 .

charge

distribution is

involved,

the

Fourier

transform

willbe

different.

8.2.4.

Example.

The example above deals with the electrostatic potential of a point

charge.

Letus now

consider

thecase

where

the

charge

distributed

overa

finite

volume.

Thenthe

potential

) =

fff

qp(r')

per')

Ir'

_ r] x q

II'"'

_ r] x ,

where

qp(r')

is the

charge

density

atr'.andwe haveuseda single

integral

because

3x'

already

indicates

the

number

integrations

tobeperformed.Notethatwehavenormalized

(1'"')

sothat its integraloverthevolmne is

Figore 8.7 showsthe geometry of the situation.

Making

a changeof

variables,

r' - r, or r' = R +r, andd

x' = d

X, with

R",

(X,

Z),

we get

V(k)

(211:~3/2f

3xe-

ik.rq

P(RR+

X. (8.30)

evaluate

Equation

(8.30),we

substitute

forpeR+r) in terms of its

Fourier

transform,

peR +

fd3k'p(k')eik'.(R+r).

(8.31)

(211:)3/2

Combining (8.30) and (8.31), we obtain

ik'·R

V(k)

=.s..f d

3xd

3k'_e

p(k')i

r.(k'-k)

(211:)3

ik'·R

3k'_e

-(k')

(_1_

f d

3xe

r.(k'-kl)

q R p

(211:)3

-...::.:.....:.....:.~--~

~(k'-k)

(8.32)

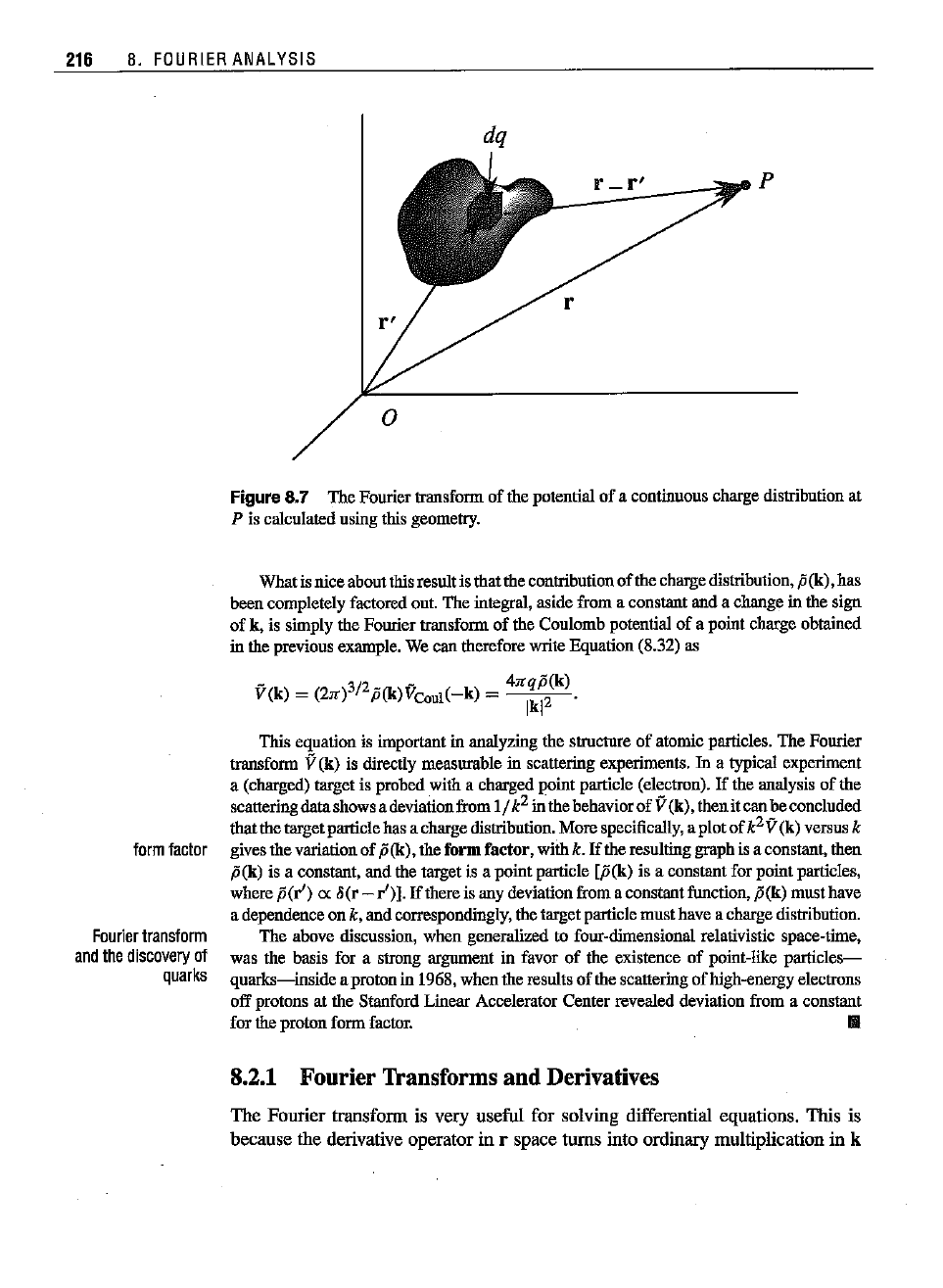
216

FOURIER

ANALYSIS

Figure8.7 The

Fourier

transform

of the

potential

of a

continuous

charge

distribution

P is calculated usingthis

geometry.

What

isnice

about

this

result

that

the

contribution

ofthe

charge

distribution,

p(k), has

beencompletely

factored

out.The

integral,

asidefroma

constant

anda

change

in thesign

of k, is simply the Fourier transform of the Coulomb potential of a point cbarge obtained

in the

example.

Wecan

therefore

write

Equation

(8.32)as

- 3/2 -

4".qp(k)

V(k)

= (2".)

P(k)VCoul(-k)

= Ikl

•

formfactor

Fourier

transform

andthe discovery of

quarks

This

equation

important

analyzing

the

structure

atomic

particles.

The

Fourier

transform

ii(k) is

directly

measurable

scattering

experiments.

In a

typical

experiment

a (cbarged) target is probed with a charged point particle (electron).

the analysis of the

scattering

data

showsa

deviation

from

1/k

inthe

behavior

of V(k),theniteanbe

concluded

that the target particle has a charge distribntion. More specifically,a plot ofk

(k) versus k

givesthe

variation

of p(k:),theformfactor,withk.1fthe

resulting

graph

isa

constant,

then

p(k)

is a constant, and the target is a point particle

[p(k)

is a constant for point particles,

where

p(r')

ex8(r -

r')].

there is any deviation from a constantfunction,

p(k)

mnst have

dependence

onk,and

correspondingly,

the

target

particle

musthavea

charge

distribution.

The abovediscussion, when

generalized

to four-dimensional relativistic space-time,

was the basis for a

strong

argument

favor

of the existence of

point-like

particles-

qnarks-inside

aproton in 1968,when the results

the scattering of high-energy electrons

off

protons

atthe

Stanford

Linear

Accelerator

Center

revealed

deviation

from

constant

~~~oofu~~~

•

8.2.1 Fourier Transformsand Derivatives

The

Fourier

transform

very

useful

for

solving

differential

equations.

This

because

the

derivative

operator

space

turns

into

ordinary

multiplication

in k

Jzn

dky(k)(ik)e

ikx,

f(x)

Jzn

dkJ(k)e

ikx.

8.2

THE

FOURIER

TRANSFORM

217

space.

For

example, if we differentiate f

(r)

in Equation (8.23) with respect to xi-

we obtain

fer)

= I f

dnk~ei(klXl+.+kjxj+

..+k"x")J()<)

aXj (2rr)n/2 aXj

(2rr~n/2

fdnkCikj)e

ik.r

J(k).

That is, every time we differentiate with respect to any component of r, the cor-

responding component of k "comes down." Thus, the n-dimensional gradient

is V

fer)

= (2rr)-n/2 f dnkCik)e

ik.r

J()<), and the n-dimensional Laplacian is

fer)

= (2rr)-n/2 f

d"k(_k

2)eik.r

J(k).

We shall use Fourier transforms extensively in solving differential equations

later in the book. Here, we

can

illustrate the above points with a simple example.

Consider the ordinary second-order differential equation

+Ci

+CoY =

f(x),

where Co,

Cl,

and C2 are constaots. We

can

"solve" this equation by simply

substituting the following in it:

y(X)

Jzn

fdkYCk)e

ikx,

dky(k)k

2eikx,

dx? ./'iii .

This gives

Jzn

dky(k)(-C2

iCt

+Co)e

ikx

Jzn

dkJ(k)e

Equating the coefficients of e

ikx

on both sides, we obtain

- k _

J(k)

) -

-C2k2

+iCik:+

Co'

we know

J(k)

[which can be obtained from

f(x)],

we can calculate

y(x)

by Fourier-transforming Y(k). The resulting integrals are not generally easy to

evaluate.

In some cases the methods of complex analysis may be helpful; in others

numericalintegrationmay be the last resort. However, the real powerof the Fourier

transform lies in the formal analysis of differential equations.

8.2.2 The Discrete Fourier Transform

The preceding remarks alluded to the power of the Fourier transform in solving

certaindifferential equations.

such a solution is combined with numerical tech-

niques, the integrals must be replaced by sums. This is particularly troe if our

218

FOURIER

ANALYSIS

function is given by a table rather than a mathematical relation, a common fea-

ture of numerical analysis. So suppose that we are given a set of measurements

performed in equal time intervals of

I'>t.Suppose that the overall period in which

these measurements are done is T. We are seeking a Fouriertransform

this finite

set of data. First we write

or, discretizing the frequency as well and writing

CUm

= m

Sco,

with

I'>cu

to be

determined later, we have

N-l

j(ml'>cu) =

f(nl'>t)e-

(mh.w

n6.t ( - ) •

v'2IT

n~O

(8.33)

Since the Fourier transform is given in terms

a finite sum, let us explore the

idea

writing the inverse transform also as a sum. So, multiply both sides of the

above equation by [e

(mh.w

k6.t /(v'2IT)]l'>cu and sum over m:

N-l

I'>

N-lN-l

L j(ml'>cu)e

(mh.w)k6.t

I'>cu

L L f(n!'>t)e

h.w6.t(k- n)

v'2IT

m~O

2:n:

n~O

m~O

I'>

N-l

f(nl'>t)

L e

h.w6.t (k- n).

2:n:N

n~O

m=O

Problem 8.2 shows that

N-l

!!J..

w8.t (k- n) =

. e

t1wt:J.t(k-n) _ 1

eili.wAt(k n) _ 1

k = n,

k # n.

Wewant the sumtovanish

whenk

# n.This suggestsdemandingthat NI'>cul'>t(k-

be an integer multiple

2:n:.

Since

I'>cu

and I'>tare to be independent of this

(arbitrary) integer (as well as

k and n), we must write

2:n:

I'>cul'>t(k

- n) =

2:n:(k

- n)

I'>cu

N =

2:n:

I'>cu

= T

discrete

Fourier

With this choice, we have the following discreteFourier

transforms:

transforms

2:n:j

cu·

} - T '

(8.34)

8.2 THE

FOURIER

TRANSFORM

219

where we have redefined the new 1to be .J2rcN/ T times the old

Discrete

Fourier

transforms

areused extensively in numerical calculation of

problems in which ordinary Fourier transforms are used. For instance, if a dif-

ferential equation lends itselfto a solution via the Fourier transform as discussed

before, then discrete Fourier transforms will give a procedure for fiuding the so-

lution uumerically. Similarly, the frequeucy analysis of signals is nicely handled

by discrete Fourier transforms.

It turns out that discrete Fourieranalysis is very iuteusive computationally. Its

present status as a popular tool iu computational physics is due primarily to a very

fast

Fourier

efficieut method

calculatiou known as the

fast

Fourier

transform.

10a typical

transform

Fouriertransform, one has to perform a sum of N terms for every point. Since there

are

N points to transform, the total computational time will be of order N

•

10the

fast Fourier transform, one takes

N to be even and divides the sum into two other

sums,one overtheeventermsandone overthe odd

terms.

Thenthecomputation

time will be of order 2 x

/2)2,

half

the original calculation. Similarly,

is even, one can further divide the odd and even sums by two and obtain a

computationtime of4 x (N/4)2, or aquarter

the originalcalculation. 10general,

if N

= 2

, then by dividing the sums consecutively, we end up with N transforms

to be performed after k steps. So, the computation time will be

= N log2 N.

For

N = 128, the computation time will be 100log2 128 = 700 as opposed to

128

R<16,400, a reduction by a factor of over 20. The fast Fourier transformis

indeed fast!

8.2.3 The Fourier Transformof a Distribution

Although one can define the Fourier transform

a distribution in exact analogy

to an ordinaryfunction, sometimes it is convenient to define the Fourier transform

of the distribution as a linearfunctional.

Let us ignore the distinction between the two variables

x and k, and simply

define the Fourier transform of a function

f :

--->

- 1 1

. t

f(u)

= = f(t)e'U

dt.

'\! 2rc

-00

Now we consider two functions, f and g, and note that

100

1 1

(j,

f(u)g(u)du

f(u)

g(t)e-'U'dt]

-00 -00

v2n-00

1 1

g(t)

[--

f(u)e-'U'du

-00

../iii-oo

g(t)l(t)

(I,

g) .

The following definition is motivated by the last equation.

220

FOURIER

ANALYSIS

8.2.5. Definition.

Let

be a distribution and let f be a

er;

function whoseFourier

transform

1exists and is also a

er;

function. Then we define the Fourier transform

ifJ

to be the distribution given by

(ifJ,

(<p,

•

8.2.6. Example. TheFouriertransform of8(x) is givenby

- - - 1 1

(8,

= (8,

= frO) =

f(t)

",21l'

-00

i:(~)f(t)dt=(~,f).

Thus,g=

1/$,

expected.

The

Fourier

transform of }j(x -

x')

ee8

(x) is givenby

- -

1 1

-ix't

= (8

f(x)

f(t)e

",,21l'"

-00

= 1

(_I_

- 'x't)

f(t)dt.

-00

Thus,if ,,(x) = 8(x - x'), then';;(t) = (1/

$)e-'x't.

8.3 Problems

III

8.1. Consider the function

frO)

L~=-oo

8(0 -

Zmn}.

(a) Show that f is periodic

period

2".

(b) What is the Fourier series expansion for

f(O).

8.2. Break:the sum

L~~-N

ein(O-O') into

L;;L;

+1+

L~~t.

Use the geometric

sum formula

N r

_ 1

~arn=a~

'::'

L..J

r-1

n=O

to obtain

e'n(O-O')

=e'(O-O')

e'N(O-~')

- 1 =

ei~(N+l)(O-O')

sin[~N(O

- Of)].

t:1

e'(O-O)

- 1

sin[~(O

0')]

By changing n to

-n

or equivalently, (0 - Of)to

-(0

- Of)find a similar sum from

-N

-I.

Now put everythiog together and use the trigonometric identity

2cos a sin P=

sin(a

to show that

'n(O-O') _

sin[(N

~)(O

- Of)]

e - 1 .

n~-N

sin[Z(O -

0')]

8.3

PROBLEMS

221

8.3. Find the Fourier series expansion

the periodic function defined on its fun-

damental cell as

!(8)

{-1(1f+8)

-1f

< 0,

1(1f

-8)

if 0 < 8

tt,

8.4. Show that An and B"

inEquation

(8.2) are real when

!(8)

is real.

8.5. Find the Fourier series expansion

the periodic function

!(8)

defined on its

fundamental cell,

(-1f,

zr), as

!(8)

cosa8,

(a) when a is an integer. (b) when a is not an integer.

8.6. Find the Fourier series expansion of the periodic function defined on its fun-

damental cell,

(-1f,

x),

!(8)

= 8.

8.7. Considerthe periodicfunctionthat is defined on its fundamentalcell,

(-a,

a),

!(x)

= [z],

(a) Find its Fourier series expansion.

(b) Evaluate both sides

the expansion at x = 0, and show that

L..,

(2k +1)2.

k=O

areevaluated at x = a.

8.8. Let

!(x)

= x be a periodic function defined over the interval (0, 2a). Find

the Fourier series expansion of

f .

8.9. Show that the piecewise parabolic "approximation" to a

sin(1fxja) in the

interval

(-a,

a) given by the function

!(x)

= {4X(a +

if - a

4x(a-x)

O~x~a

hasthe

Fourier

series

expansion

32a

1 . (2n +1)1fx

!(x)

= ---;3

(2n + 1)3 sm a .

Plot

!(x),

sin(1fxja), and the series expansion (up to 20 terms) for a = I

between

-I

and +I on the same graph.

8.10. Find the Fourierseries expansion

!(8)

= 8

for

181

. Thenshow that

and

1f2

(_I)"

---~

12 -

L..,

•

n=l

222

FOURIER

ANALYSIS

8.11. Find the Fourier series expansion of

f(t)

= {Sinwt if

0::;

t ::;nf

o»,

o if -

rr/w::;

t::;

8.12. What is the Fourier transform of

(a) the constant function f (x) = C, and

(b) the Dirac delta function

8(x)?

8.13. Show that

(a) if

g(x)

is real, then

g*(k)

= g(

-k),

and

(b)

g(x)

is even (odd), then g(k) is also even (odd).

8.14. Let gc(x) stand for the single function that is nonzero only on a subinterval

of the fundamental cell

(a, a +L). Define the function

g(x)

= L gc(x -

jL).

j=-oo

(a) Show that

g(x)

is periodic with period L.

(b) Find its Fourier transform g(k), and verify that

g(k) = Lgc(k) L

8(kL

- 2mrr).

m=-oo

transform

g(k), and show that it is the Fourier

series

gc(x).

8.15. Evaluate the Fourier transform of

g(x)

blxl/a

[x] < a,

[x] > a.

8.16.

Let

f(6)

be a periodic function given by

f(6)

I:~-oo

ane

tlle.

Find its

Fourier transform

/(t).

8.17. Let

ItI< T,

if ItI> T.

Show that

/(w)

_1_

{Sin[(W- "'O)T] _ sin[(w +

wa)T]}

"J2ii

w -

w +

"'0

Verify the uncertainty relation

!'>w!'>t

RJ 4rr.