Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


7.7
PROBLEMS
193
7.21. Use the generating function for Legendrepolynontialsto show that P
n
(I)
=
I,
Pn(-I)
=
(_I)n,
Pn(O)
= 0 for odd n, and
P~(l)
=
n(n
+1)/2.
7.22. Both electrostatic andgravitationalpotentialenergies depend onthe qnantity
I/lr
- r'], where
r'
is the position
of
the sonrce (charge or mass) and r is the
observation point.
(a) Let r lie along the z-axis, and nse spherical coordinates and the definition of
generating functions to show that
_1_
=
~
f(r<)n
Pn(cose),
[r -
r']
r-; n=O r-;
where r
«r»
is the smaller (larger) of
rand
r',
and eis the polar angle.
(b) The electrostatic or gravitational potential energy
<!>(r)
is given by
<!>(r)
=
kll!
p(r
')
d
3
x
'
,
[r -
r']
where k is a constant and
p(r')
is the (charge or mass) density function. Use the
result
of
part (a) to show that
if
the density depends only on
r',
and not on any
angle (i.e.,
p is sphericallysymmetric),then
<!>(r)
reduces to the potential energy
of a point charge at the origin for r > r',
(c) What is <!>(r)-in the form
of
an
integral-for
r < a for a spherically sym-
metric density that extends from origin to a?
(d) Show that E (or g) is given by
[kQ(r)lr
2
]e
r
where Q(r) is the charge (or
mass) enclosed in a sphere of radius
r,
7.23. Use the generatingfunction for Legendrepolynontials and their orthogonal-
ity to derive the relation
1
1
dx
2 =
ft
2n
1
1
P;(x)dx.
_11-2xt+t
n=O
-1
Integrate the LHS, expand the result in powers of t, and compare these powers on
both sides to obtain the normalization constant h
n
•
7.24. Evaluate the following integralsusing the expansion of the generating func-
tion for Legendre polynontials.
10
" (a cos s +b)
sine
de
(a) .
o -v'a
2+2abcose+b
2
7.25. Differentiate the expansionof the Legendrepolynontial generating function
with respect to
x and manipulate the resulting expression to obtain
00 00
(I -
2xt
+t
2
)
:~:::>n
P~(x)
= t
~::>n
Pn(x).
n=O n=O

if
k is even,
194 7. CLASSICAL
ORTHOGONAL
POLYNOMIALS
Equate equal powers of t ou both sides to derive the recurrence relation
, , ,
P
n
+
1
+P
n-
1
-
2xP
n
- P
n
=
O.
7.26. Show that
[1
Pk(X)
dx
= {8
kO
io
(_I)(k-l'/2(k_l)!
S",==:fu2-"
if
k is odd.
2
k
(y )!(
&¥
)!
Hint: For even k,extend the region of integration to
(-I,
I)
and use the orthogo-
nality property. For odd k, note that
d
k
-
1
2 k 1
dx
k
-
1
(I-x)
10
gives zero for the upper limit (by Lemma 7.1.3). For the lower limit, expand the
expression using the binomial theorem, and carry out the differentiation, keeping
in mind that only one term of the expansion contributes.
7.27.
Showthatg(x,
r) =
g(-x,
-t)forbothHermiteandLegendrepolynomiais.
Now expand
g(x,
t) and
g(
-x,
-t)
and compare the coefficients
of
t" to obtain
parity
relations
the
parity
relations for these polynomials:
and
Pn(-x)
=
(_I)n
P,,(x).
7.28. Derive the orthogonality of Legendre polynomials directly from the differ-
ential equation they satisfy.
7.29. Expand Ixlin the interval
(-I,
+1)
in terms of Legendrepolynomials. Hint:
Use the result
of
Problem 7.26.
7.30. Apply the general formalism of the recurrence relations given in the book
to find the following two relations for Laguerre polynomials:
v v
dL~
(a)
nL
n
- (n
+
v)L
n_1
-
x
dx
=
O.
(b) (n +
I)L~+1
- (2n +v +I -
x)L~
+(n +
v)L~_1
=
O.
7.31. From the generating function for Laguerre polynomials given in Table 7.2
deduce that
L~(O)
=
r(n
+v +
I)/[n!r(v
+I)].
7.32. Let L
n
sa L2. Now differentiate both sides of
e-xt/(l-t)
00
g(x,t)=
I-t
=
LtnL,,(x)
o
with respect to x and compare powers
of
t to obtain
L~
(0) =
-n
and
L~
(0) =
~n(n
-
I).
Hint: Differentiate
1/(1
- t) =
I:;;:o
t" to get an expression for
(I -
t)-2.

7.7
PROBLEMS
195
7.33.
Expande-
kx
as a series
of
Laguerrepolynomials
L~
(x). Findthe coefficients
by using (a) the orthogonality of
L~(x)
and (b) the generating function.
7.34. Derive the recurrence relations given in the book for Jacobi, Gegenbauer,
and Chebyshev polynomials.
7.35. Show that
Tn(-x)
=
(-I)nTn(x)
and Un
(-x)
=
(-I)nun(x).
Hint: Use
g(x,
t) =
g(-x,
-t).
7.36. Show that Tn(l) = I,
Un(l)
= n + I,
Tn(-I)
=
(_I)",
Un
(-I)
=
(-I)n(n
+
I),
T2m(O)
=
(_l)m
=
U2m(O),
and
T2m+l(O)
= 0 =
U2m+!
(0).
Additional Reading
J. Dennery, P.and Krzywicki, A. Mathematicsfor Physicists, Harperand Row,
1967. Treats the classicalorthogonalpolynomialsin the spirit of this chapter.
2. Tricomi,
F. Vorlesungen uber Orthogonalreihen, Springer, 1955. The origi-
nal unified treatment of the classical orthogonal polynomials.

8,
_
Fourier
Analysis
The single most recurring theme of mathematical physics is Fourier analysis.
It
shows up, for example, in classical mechanics and the analysis of normal modes,
in electromagnetic theory and the frequency analysis
of
waves, in noise consid-
erations and thermal physics, in quantum theory and the transformation between
momentum and coordinaterepresentations, and in relativistic quantumfieldtheory
and creation and annihilation operation formalism.
8.1 Fourier Series
One way to begin the study of Fourier series and transforms is to invoke a general-
ization of the Stone-Weierstrass ApproximationTheorem (Theorem 5.2.3), which
established the completeness of monomials,
x
k
.
The generalization of Theorem
5.2.3 permits us to find another set
of
orthogonal functions in terms
of
which
we can expand an arbitrary function. This generalization involves polynomials in
more than one variable (For a proof
of
this theorem, see Sinunons [Sinun 83, pp
160-161].)
generalized
Stone-Weierstrass
theorem
8.1.1. Theorem. (generalized Stone-Weierstrasstheorem) Suppose that
!(X\,
X2,
...
, x
n)
is continuous in the domain {ai ::: Xi ::: hi
li=\.
Then it can be expanded
interms
of
themonomials
X~l
X~2
••.
x~n
, wherethek; are nonnegative
integers.
Now let us consider functions that are periodic and investigate their expan-
sion in terms
of
elementary periodic functions. We use the generalized Stone-
Weierstrass theorem with two variables,
x and y. A function
g(x,
y) can be written
as
g(x,
y) =
I:k,m~o
akmxkym.
In
this equation, x and y can be considered as co-
ordinatesin thexy-plane,
whichin tum can be writtenin terms
of
polarcoordinates

8.1
FOURIER
SERIES
197
r and
e.
Inthat case, we obtain
00
[(r,
e) sa
g(r
cos
s,
r
sine)
= L akmrk+m cos
k
esin" e.
k,m=O
In
particular, if we let r = I, we obtain a function of ealone,
which
upon substi-
tution of complex exponentials for sin
eand cos ebecomes
(8.1)
where
b" is a constant that depends on akm' The RHS of (8.1) is periodic with
period
2IT;thus, it is especially suitable for periodicfunctions
[(e)
that satisfy the
periodicity condition
[(e
- IT) =
[(e
+IT).
We
can
also write Equation (8.1) as
00
[(e)
= bo+L (b"ei"e +b_"e-i"e)
n=l
00
= bo+
L[(b"
+b_,,) cosne +i(b" - b_,,) sinne)]
n=l
'"-r--'
.,
I
=A
n
=B
n
00
= bo+
L(A"
cosne +B" sinne).
n=l
(8.2)
If
[(e)
is real, then bo,
A",
and B" are also real. Equation (8.1) or (8.2) is called
the
Fourierseries
expansion
of
[(e).
Let
us now concentrate on the elementary periodic functions ei"e. We define
the
(Ie,,)
}~I
such that their
"eth
components" are given by
1 . e
(ele,,) =
l'C:e"',
-v2IT
where eE
(-IT,
IT).
These
functions-or
ket
vectors-which
belong to .(,2(
-IT,
IT), are orthonormal,
as can be easily verified.
It
can also be shown that they are complete.
In
fact,
for functions that are
continuous on
(-IT,
IT), this is a result of the generalized
Stone-Weierstrass theorem.
It
turns out, however, that (Ie,,)
}~I
is also a complete
orthonormalsequence for
piecewisecontinuousfunctions on
(-IT,
IT).I Therefore,
any periodic piecewise continuous function of
e
can
be expressed as a linear
combination
of
these orthonormal vectors. Thus if
If)
e.(,2(
-IT,
IT),then
00
If)
= L
["
Ie,,),
n=-oo
where f" =
(e,,1
f).
(8.3)
1Apiecewise
continuous
function
onafinite
interval
isone
that
hasafinite
number
ofdiscontinuitiesinits
interval
of
definition.

198 8.
FOURIER
ANALYSIS
We can write this as a functional relation if we take the Othcomponent of both
sides:
(01
f)
=
'£':::-00
fn
(01
en), or
Fourier
series
expansion:
anguiar
expression
f(O) =
_1_
f fnein9
.[iii
n=-oo
with fn givenby
(8.4)
fundamental
cell
ofa
periodic
function
"The
profound
study
of
nature
is
the
most
fruitful
source
of
mathematical
discoveries."
Joseph
Fourier
fn = (enI1
If)
= (enl
(j~
10)(01
dO)
If)
=
L:
(enl 0)
(01
f)
so
=
-1-1"
e-
in9
f(O)dO.
(8.5)
.[iii
-"
It
is important to note that even though f (0) may be defined only for -:n:
:0:
o
:0:
:n:,
Eqnation (8.4)extendsthe domainof definitionof
f(O)
to all theintervals
(2k -
I):n:
:0:
0
:0:
(2k+
I):n:
for all k E Z. Thns, if a functionis to be represented
by Equation (8.4) withoutany specificationof the intervalof definition,itmust be
periodic in
O.For such functions, the interval of their definitioncan be translated
bya factor
of2:n:.Thus, f(O) with -:n:
:0:
0
:0:
:n:
is equivalentto f(O -
2m:n:)
with
2m:n:
-:n:
:0:
0
:0:
2m:n:
+:n:; both will givethe same Fourier series expansion.We
shall defineperiodicfunctions in their fundamental cell such as
(-:n:,
:n:).
JosephFourier(1768-1830)did
very
wellasa
young
student
of
mathematics
buthadset his
heart
on becoming an
army
officer. Denied a commission because he was the son
of
a
tailor,
he wentto aBenedictine schoolwiththehope
that
he
couldcontinue
studying
mathematics
atits
seminary
in
Paris.
The
French
Revolution
changed
those
plans
andsetthestage
formany
ofthe
personal
circumstances
of
Fourier's
lateryears,
duein
part
tohis
courageous
defenseof some of its victims,
an
action
that
ledto his
arrest
in 1794.Hewas
released
later
that
year,
andhe
enrolled
asa
student
in theEcoleNonnale,
which
opened
and
closed
within
a
year.
His
performance
there,
however,
was
enough
toeamhima
position
as
assistant
lecturer
(under
Lagrange
and
Monge)
in theEcole Poly
technique.
He was anexcellent
mathematical
physicist, was a
friend
of
Napoleon
(sofarassuchpeoplehave
friends),
and
accompanied
himin1798to
Egypt,
where
Fourier
held
various
diplomatic
and
administrative
postswhilealso
conducting
research.
Napoleon
tooknoteof his
accomplishments
and,
on
Fourier's
return
to
France
in 1801,
appointed
him
prefect
of the
district
of Isere,in
southeastern
France,
andin this
capacity
builtthe
first
real
road
from
Grenoble
to
Turin.
He also
befriended
theboy
Champollion,
who
later
deciphered
theRosetta stone as the
first
long step
toward
understanding
the
hieroglyphic writing of the ancient Egyptians.
Like
other
scientists
of his
time,
Fourier
tookup the flow of
heat.
The flowwas of
interest
as a
practical
problem
in the
handling
of
metals
in
industry
and
as a
scientific
problem
in
attempts
to
determine
the
temperature
inthe
interior
of the
earth,
the
variation

Fourier
series
expansion:
general
expression
8.1
FOURIER
SERIES
199
of that temperature with time, and other such questions. He submitted a basic paper on
heat conduction to the Academy of Sciences of Paris in 1807. The paper was judged
by
Lagrange, Laplace,
and
Legendre.
The
paper
was
not
publish<id,
mainly
due
to the objections
of
Lagrange, who
had
earlierrejected the use
of
trigonometric series.
But
the Academy did
wish to encourageFourier to develop his ideas, and
So
made the problemof the propagation
of heatthe subject
of
a grandprizeto be awardedin 1812. Fouriersubmitteda revisedpaper
in 1811, which was judged by the
men
alreadymentioned and others. It won the prize but
was criticized for its lack
of
rigor and so was not published at that time in the Memoires
of
the Academy.
He developeda mastery
of
clearnotation, some
of
whichis still in use today. (The mod-
ern integral sign and the placement
of
the limits
of
integration nearits top and bottom were
introduced by Fourier.) It was also his habit to maintain close association between mathe-
maticalrelations and physically measurable quantities, especially in limiting or asymptotic
cases, even performing some
of
the experiments himself. He was one
of
the first to begin
full incorporation of physical constants into his equations, and
made
considerable strides
towardthe modern ideas
of
units and dimensional analysis.
Fourier continued
to work on the subject
of
heat and, in 1822, published one of the
classics
of
mathematics, Theorie Analytique de la Chaleur, in which he
made
extensive
use
of
the series that now
bear
his
name
and incorporated the first
part
of
his 1811 paper
practically without change. Two years laterhe
became
secretary
of
theAcademy and was
able to have his 1811 paperpublished in its original form in the
Memoires.
Fourier
series were
of
profound significance in connection with the evolution
of
the
concept
of
a function, the rigorous theory
of
definite integrals, and the development
of
Hilbert
spaces.Fourierclaimedthat"arbitrary"graphs
can
be representedby trigonometric
series and should therefore be treatedas legitimatefunctions, and it cameas ashockto many
that he
tumed
out to be right. The classical definition
of
the definite integraldue to Riemann
was first given in his fundamental
paper
of 1854 on the subject
of
Fourier series. Hilbert
thought
of
a function as represented by an infinite sequence, the Fourier coefficients
of
the
function.
Fourierhimselfis one
of
the fortunate few: his
name
has become rooted in all civilized
languages as an adjective that is well-known to physical scientists and mathematicians in
everypartof theworld.
Functions are not always defined on
(-17:,17:).
Let
us consider a function
F(x)
that is defined on (a, b) and is periodic with period L = b - a. We define a new
variable,
and note that
f(O)
==
F«LI217:)O +a +L12) has period (-17:,17:) because
f(U17:)
= F
(2~
(0
±1r)+a
+~)
= F
(x
±~)
and
F(x
+L12) =
F(x
-
LI2).
If
follows that we can expand the latter as in
Equation (8.4). Using that equation, but writing
0 in tenus of x, we obtain

(8.6)
200
8.
FOURIER
ANALYSIS
F(X)=F(~8+a+£)=_I-
f !n exp [in
2:n:
(x-a-£)]
.
2:n:
2../iii
n=-oo L 2
= _1_ f
Fne2mrixjL,
4 n=-oo
where we have introduced- F
n
sa '/L/2:n:!ne-i(2nn/L)(a+L/2). Using Equation
(8.5), we
can
write
t;
=
[Le-
i(2nn/L)(a+L/2)_I_
In
e-
inO
!(8)d8
V
2;.
../iii
-n
= 4 e-i(2nn/L)(a+L/2)l
a
+
L
e-i(2nn/L)(x-a-L/2)
F(x)
2:n:
dx
~
a L
=
_1_1
b
e-
i(2nn/L)x
F(x)dx.
(8.7)
4a
The
functions exp(2:n:inx/
L)/4
are easily seento be orthonormal as mem-
bers
of
.c}(a, b). We can introduce
{len)}~1
with the
"xth
component" giveu by
(xl
en) =
(1/4)eZrrinx/L.
Then
the reader
may
check that Equations (8.6) and
(8.7) can be written as
IF) =
L~-oo
F
n
len) with F
n
=(nl F).
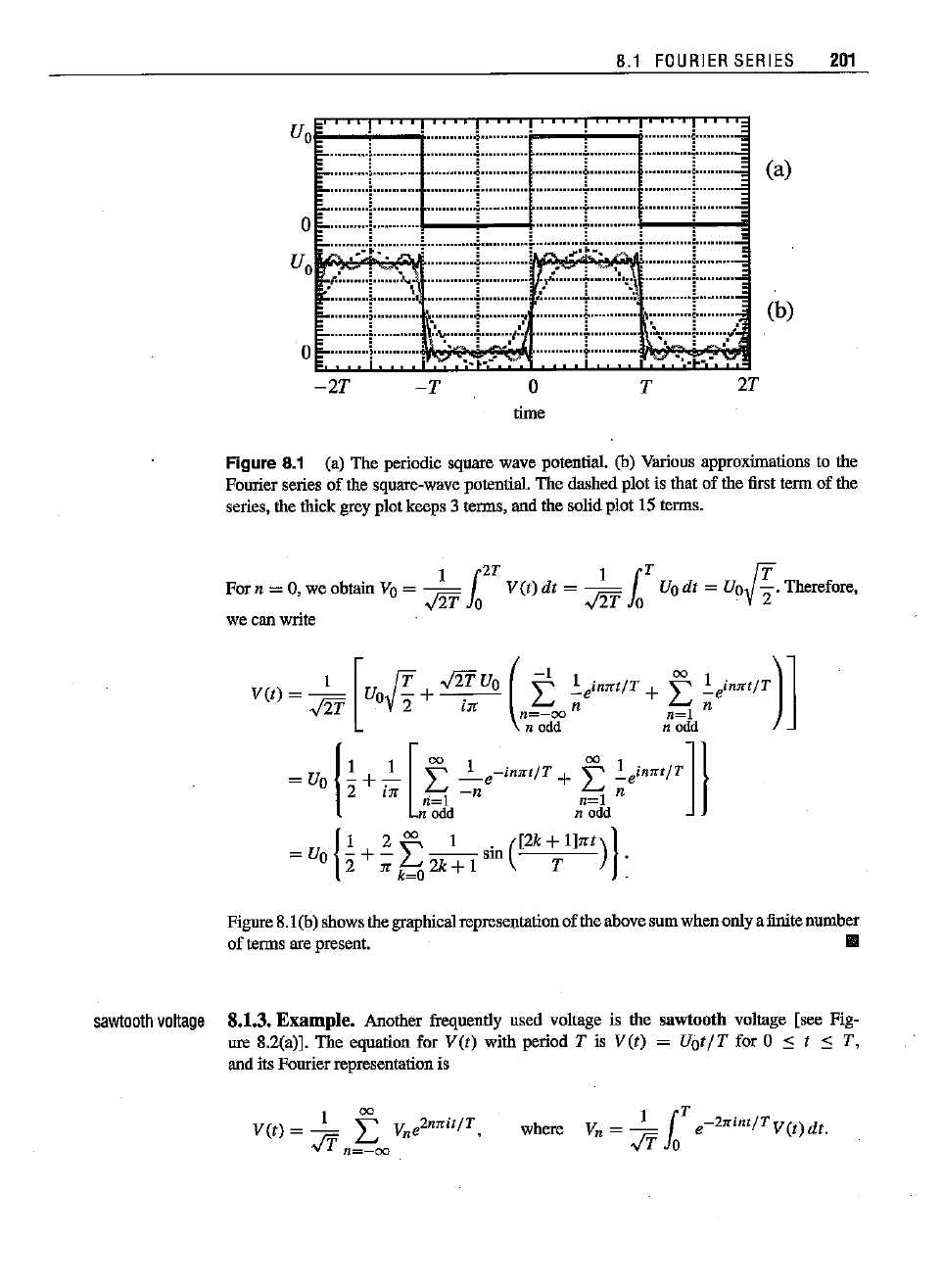
8.1.2.Example. In the study of electricalcircuits,periodicvoltage signalsof different
square
wave
voltage
shapes
are
encountered.
An
example
isasquarewavevoltageof height Uo.
"duration"
T,
and"rest dnration"T [seeFignre 8.I(a)]. The potential as a functionof time Vet) canbe
expanded
asa
Fourier
series.
The
interval
is (0,
2T)
because
that
is onewholecycleof the
potential
variation.
We
therefore
use
Equation
(8.6)andwrite
I
00
Vet) =
--
L Vn,e2n1fitj2T,
..tiTn=-oo
I Jo2T .
where V
n
=
-_
e-
2n,nt/2T
V(t)dt.
..tiT
0
The
problem
is tofindV
n
.
Thisis easilydoneby
substituting
V t _ {Uo if 0 s t ::; T,
( ) - 0
if
T s t s
2T
in the lastintegral:
V
n
=
Uo
fT
e-innt/T
dt = Uo
(_~)
[(_I)n
_ I] where n
i'
0
..tiT
1
0
..tiT
1n1f
_
{O
ifn
is even
andn
=1=
0,
-
..tiTuo
if
. odd
. n IS .
1n1f
2TheF
n
are
defined
suchthatwhatthey
multiply
in the
expansion
are
orthonormal
inthe
interval
(a, b).
8.1
FOURIER
SERIES
201
(b)
(a)
2T
T
-T
u
0
"-..••....
+...........
:::::::::::t:::::::::::
+ !
::::::::::::1:::::::::::
••••••
·••• l
•••••
··•····
.••..•••••••
..:.............
•
•••••••••••
(10............
.
~
.
o
:~:~:~:~:r:::::~:~:~I::::::::::::L:::::::::I:~:~:~:~::~:L:~:~:~:~:l:::::::::::I:::::.:.~
-.::.-
--.-:
: ;
--:;;.:
:
U
o
.:10............
..
~
.
,~l~'.~~H~;
f~~~:~·~~~~~
-2T
Figure 8.1 (a) The
periodic
square
wave
potential.
(b)
Various
approximations
to the
Fourier
series
of
the
square-wave
potential.
The
dashed
plotis
that
of the
first
term
of the
series, the thick grey plot keeps 3 terms, and the solid plot IS terms.
I 1
2T
I I
T
~
For n = 0, we obtain Vo= "'"' V(t) dt = "'"' Uodt = Uo
-.
Therefore,
..,2T 0
..,2T
0 2
wecan
write
V(t) =
_1_
[uo
f'f+
,fiT
Uo ( I:
!e
imrt/
T
+
f:
!e'nm/T)]
,.j2f
V
"2
Z:Tr
n=-oo
n
n=l
n
n odd n odd
= Uo
{!
+
~
If:
_I
e-in"t/T
+
f:
!e
in
m/
T]}
2 l1r
n=l
-n
n=l
n
odd n odd
= U
{!
~
~
_1_
in
([2k+
1
1
1f
t)}
o
2+1ft;Q2k+l
s
T .
Figure
8.1(b)showsthe
graphical
representation
ofthe
above
sumwhenonlya
finite
number
oftenusare
present.
..
sawtooth
voltage
8.1.3. Example. Another frequently nsed voltage is the sawtooth voltage [see Fig-
ure 8.2(a)]. The equatiou for
V(t)
with period T is Vet) =
UotlT
for 0
~
t
~
T,
andits
Fourier
representation
is
I
00
V(t)
= - L Vne2n1titjT,
Jf
n~-oo
where
V
n
= _1_ r
T
e-2"int/T
V(t)
dt.
Jf
i
o

202 B.
FOURIER
ANALYSIS
Substitutingfor
V(t)
inthe integral above yields
V
n
= _1_
{T
e-21rintjTUo!.... dt =
UoT-3j2
{T
e-21rint/Tt
dt
..ti
10
T 1
0
=
ti
r-3/2(---J!--e-2Jrint/TIT +;!.-
(T
e-21rint/T
dt)
o -12mr 0 l2mr 1
0
::..::.-~--
~o
3/2
( T
2)
uo..ti
= UOT-
-.
- =
--.--
wheren t"0,
-12m/:
z2n:tr
1
leT
1
leT
t
Vo= -
V(t)
dt =
f'i'
UO-
dt
=
!Uo..ti
.
..ti
0
-rt
0 T
Thus,
V(t)
= _1_
[lUo..ti
_
uo..ti
(t
~ei2n"'/T
+
f:
~ei2n"t/T)]
...tf
2
z2rr
n=-oo
n n=l n
= Uo
{~-
2.
f:
~Sin(2mrt)}.
2
JCn=ln
T
Figure
8.2(b)showsthe
graphical
representation
of the
above
series
keeping
the
first
few
ternM. •
The foregoing examples indicate an important fact about Fourier series. At
points
of
discontinuity (for example, t = T in the preceding two examples), the
value of the functiou is not defined, but the Fourier series expansion assigns it a
value-the
average of the two values on the right and left
of
the discontinuity.
For
instance, when we substitute t = T in the series of Example 8.1.3, all the sine
terms vanish and we obtain
V(T)
= Uo/2, the average of Uo (on the left) and 0
(on the rigbt). We express this as
V(T)
=
![V(T
-
0)+
V(T
+0)] sa !lim
[V(T
-
E)+
V(T
+E)].
.....0
This is a general property of Fourier series.
In
fact, the main theorem of Fourier
series, which follows, incorporates this property. (For a proofof this theorem, see
[Cour 62].)
8.1.4.
Theorem.
TheFourierseriesofafunction f(O) that ispiecewise continuous
in the interval
(-Jr,
Jr) converges to
![f(O
+0) +f(O - 0)] for - x < 0 <
it
;
![f(Jr)
+
f(-Jr)]
for
0 =
±Jr.
Although we used exponential functions to find the Fourier expansion
of
the
two
examples
above,
it is
more
convenient to
start
with the
trigonometric
series
