Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.

B.l
FOURIER
SERIES
203
(b)
time
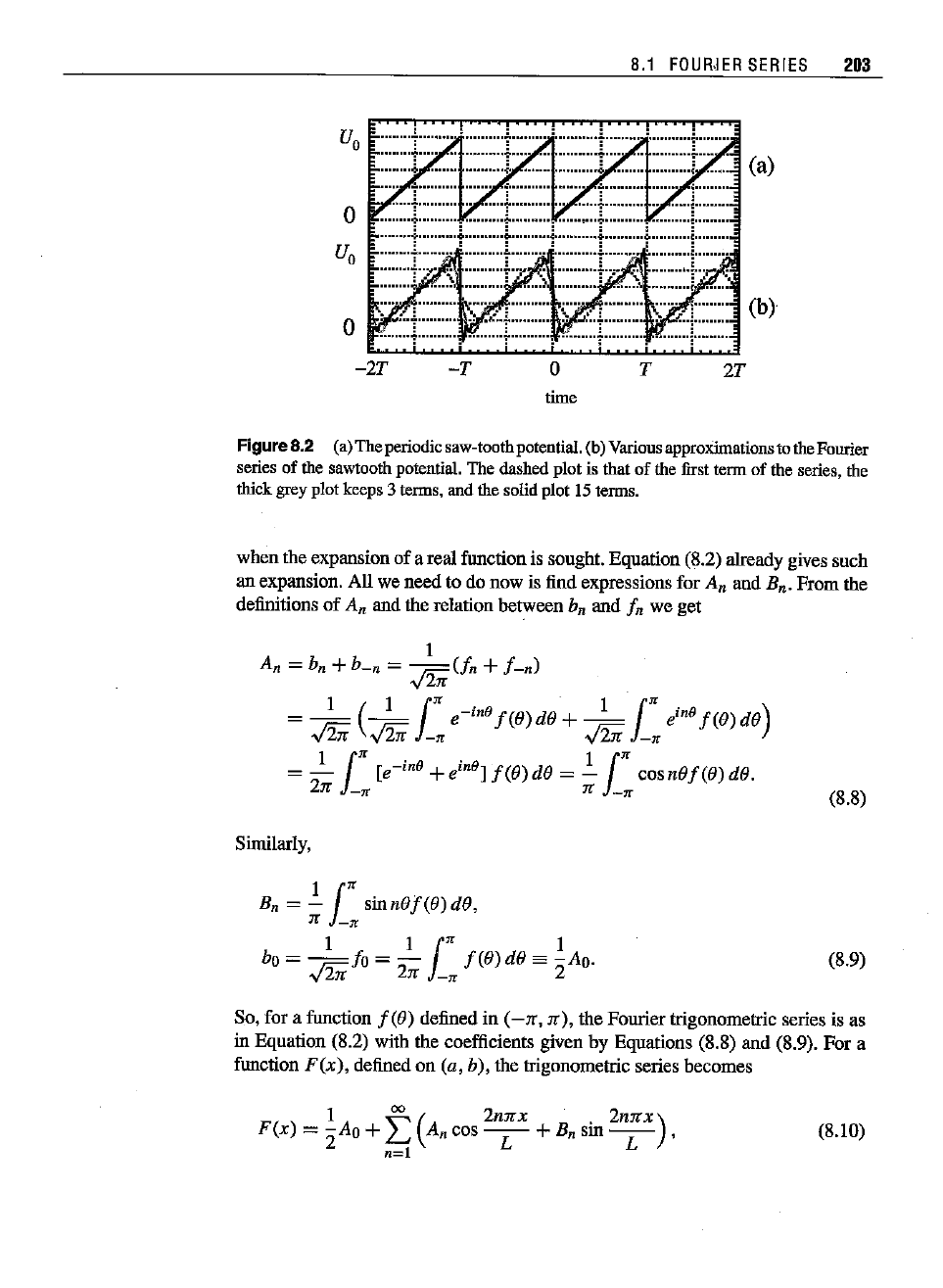
Figure8.2 (a)The
periodic
saw-tooth
potential.
(b)
Various
approximationsto
the
Fourier
seriesof the
sawtooth
potential.
The
dashed
plot is thatof the
first
term of theseries,the
thick grey plot keeps 3 terms, and the solid plot 15 terms.
when the expansion of a real function is songht. Equation (8.2) already gives such
an expansion. All we need to do now is find expressions for An and B
n.
From the
definitions
of
An and the relation between b
n
and In we get
1
An =bn +
b-
n =
!'C(fn
+
I-n)
v2re
1 I
f"
1
f"
= -
(-
e-
ine
1(0)
so
+- e
ine
1(0)
dO)
v'2ir
v'2ir
-"
v'2ir
-"
1
f"
1 L
= - [e-
ine
+eineJ/(O)dO
= - cosnOI(O) dO.
211:
-1t
tt
-11:
Similarly,
I L
B
n
= - sinnOI(O) dO,
:n:
_"
1 I
f"
I
bo =
!'Clo
=
-2
1(0)
se
es
-2
Ao.
V 2n
1!-1C
(8.8)
(8.9)
So, for a function
1(0)
defined in
(-re,
:n:),
the Fourier trigonometric series is as
in Equation (8.2) with the coefficients given by Equations (8.8) and (8.9). For a
function
F(x),
defined on (a, b), the trigonometric series becomes
1
~
( Znnx . 2n:n:x)
F(x)
= -AD +
L..
Ancos--
+B
n
sm--
,
2 n=1 L L
(8.10)

(8.11)
204 8.
FOURIER
ANALYSIS
where
An =
~
tcos
Cn;X)
F(x)
dx
;
En
=
~
(b sin
(2nrrx)
F(x)
dx.
Lin
L
A convenient rule to remember is that for even (odd)
functions-which
are
necessarily defined on a symmetric interval around the
origin-only
cosine (sine)
terms appear in the Fourier expansion.
8.1.5.
Example. An alternating currentis tnmed into a direct currentby startingwith
a signalof theform V(t)
ex:
Isin
lllt
I.i.e., a harmonic
function
thatis never
negative,
as
shown
in
Figure
8.3(a).Thenby
proper
electronics, one
smooths
outthe
"bumps"
so that
the
output
signalis very
nearly
a
direct
voltage.Letus
Fourier-analyze
the
above
signal.
Since Vet) is even for
-lC
-c tot < 1C, we expect only cosine tenus to be present.
Ifforthe
timebeingweuse e
instead
of cot,we canwriteIsinBI = !
Ao
+
L~l
Ancosn6,
where
1
1"
2
10"
A
n
= -
IsinOlcosnOdO=-
sinOcosnOdO
]'(-Jr
nO
21o"t 2
[(-I)n+
1]
= -
~[sin(n
+1)0 - sin(n
-I)O]dO
=
--2--
11:0
n-l1!
_{-~(+)
for e evenand e
ee
D,
- 1r n
-1
o forn odd,
and
Ao = (1/rr)
J':."
Isin0l dO= 4/rr. Theexpansionthen yields
. 2 4
~
cos2kwt
Ismwtl=---
L.,
2 '
rr
tt
k~l
4k - 1
where
in thesumwe
substituted
2k for n, and
OJt
for
B.
Figure
8.3(b)showsthe
graph
of
theseriesabovewhenonly the
first
few termsarekept. II
It
is useful
In
have a representation
of
the Dirac delta function in terms of
the present orthonormal basis
of
Fourier expansion. First we note that we can
represent the deltafunction in terms of a series in
any set of orthonormalfunctions
(see Problem 8.23):
8(x -
x')
= L
fn(x)t,;'(x')w(x).
(8.12)
n
Next we use the basis
of
the Fourier expansion for which
w(x)
= 1. We then
obtain
00
8(x
-x')
= L
n=-oo
e21r:inx/L
e-2ninx'/L
~
Ee
2ni
n(x-x')/
L.
n=-oo

8.1
FOURIER
SERIES
205
(a)
(b)
31C/ro
21C/ro
1C/ro
time
a
oO:"""~.L.....~..L.,..~u.....~
..........
~-'-'-~
..........
~
.........
~........"
-rc/ro
a
Figure8.3 (a) The periodic "monopolar" sine potential. (b) Various approximations to
the
Fourier
seriesofthe"monopolar' sine
potential.
The
dashed
plotis
that
ofthe
first
term
of the series, the thick grey plot keeps 3 terms, and the solid plot 15 terms.
8.1.1 The GibbsPhenomenon
The plot of the Fourier series expansions in Figures 8.1(b) and 8.2(b) exhibit a
feature that is common to all such expansions: At the discontinuity of the periodic
function, the truncated Fourier series overestimates the actual function. This is
Gibbs
phenomenon
called the
Gibbs
phenomenon,
and is the subject
of
this subsection.
Let
us approximate the infiuite series with a fiuite sum. Then
1
~
. 0 1
~
. 0 1
fo2n"
.0'
fN(O) =
--
L..
fn
eln
=
--
L..
e
ln
--
e-
In
f(O')
dO'
v'2rr
n
=- N
v'2rr
n
=- N '
v'2rr
0
1
(2n
N
=
27C
In dO'
f(O')
L ein(O-O'),
o
n=-N
where we substituted Equation (8.5) in the sum and, without loss of generality,
changed the interval of integration from
(-:n:, IT) to (0,
2:n:).
Problem 8.2 shows
that the sum in the last equation is
~
in(O-O')
_
sin[(N
+
~)(O
-
0')]
L..
e - 1
n=-N
sin['i(O -
0')]
It
follows that
fN(O)
=...!:.-
r:
s«
f(O')
sin[(N
+
~)(O
-
0')]
2"
Jo
sin[~(O
-
0')]

206 6.
FOURIER
ANALYSIS
I
i:
sin[(N
+ l)tP] I
j2n~0
= - dtPf(tP+0) . 1 2 sa -
d4>f(tP
+
O)S(tP)·
2n:
-0
s1O(2tP)
2n:
-0
(8.13)
~
=SCq,)
We
wantto
investigatethe behavior
of
fN at a discontinuity
of
f.
By translating
the limits
of
integration
if
uecessary, we can assume that the discontinuity
of
f occurs at a point a such that 0
01
a
01
2n:.
Let
us denote the
jump
at this
discontinuity for the function itselfby
!'>f,and for its finite
Foutier
sum by
!'>fN:
!'>f sa
f(a
+
f)
-
f(a
-
f),
maximum
overshoot
in
Gibbs
phenomenon
calculated
Then,
wehave
!'>fN
I
c:
I
j2n-u+<
=-
dtPf(tP+a +f)S(tP) - - dtPf(tP +a - f)S(tP)
2n
-a-e
211:
-a+€
=
_I
{j-u+<
dtPf(tP+a +f)S(tP) +
t:
dtPf(tP+a +f)S(tP)}
2rr
-a-e
-a+€
I
{j2n-u-<
c:
}
- - dtPf(tP+a - f)S(tP) + dtPf(tP+a - f)S(tP)
2n -a+€
2rr-a-e
I
{j-u+<
{2n-u+< }
=
2n:
-u-<
dtPf(tP+a +f)S(tP) -
J2n-u-<
dtPf(tP+a - f)S(tP)
I
i:
+- dtP[f(tP +a +
f)
- f(tP +a - f)]S(tP)
2n
-a+e
The first two integrals give zero because
of
the small ranges
of
integration and the
continuity
of
the integrands in those intervals. The integrand
of
the third integral is
almostzero for all values
of
the range
of
integrationexcept
when
tP
'"
O.Hence, we
can confine the integration to the small interval
(-8,
+8)
for which the difference
in the square brackets is simply
ts],
It
now follows that
!'>f
j~
sin[(N
+!)tP] !'>f
fo~
sin[(N
+!)tP]
!'>fN(8)
'"
-2
. 1
dtP
'"
- 1
dtP,
it
_~
s1O(2
tP)
n:
0 2
tP
wherewe
have emphasized
the
dependence
of
fN on 8 and approximated the sine
in the denominator by its argument, a
good
approximation
due
to the smallness
of
tP.
The
reader may find the plot
of
the integrand in Fignre 6.2, where it is
shown clearly that the major contribution to the integral comes from the interval
[0,n:1(N+!)],where
n:
I(N
+!)
is the first zero
of
the integrand. Furthermore,it
is clearthat
if
the upperlimitis largerthan
n:
I(N +
!),
the result
of
the integral will
decrease, because in
each
interval
of
length 2n:,the area below the horizontal axis
is largerthan that above. Therefore, if we are interested in the
maximum overshoot

8.1
FOURIER
SERIES
207
of the finite sum, we must set the
upperlimit
equal to re/(N+
~).
It follows firstly
that the maximum overshoot of the finite sum occurs at
re
I(N
+
~)
RJ n tN to the
right
of
the discontinuity. Secondly, the amount of the maximum overshoot is
=X
I
~
2!:>.f
1,,/(N+2)
sin[(N
+
~)</J]
(l1fN
)m", RJ - A.
d</J
tt
0
'I'
2 1
1C
sinx
=
-tV
-dx
RJ 1.179I1f.
re
0 x
Thus
(8.14)
8.1.6.Box. (Gibbs phenomenon) The finite (large-N) sum approximation
of
the discontinuousfunction overshoots thefunction
itself
at a discontinuity
by
about
18 percent.
8.1.2 Fourier Series in Higher Dimensions
It
is instructive to generalize the Fourier series to more than one dimension. This
generalizationis especiallyusefulin crystallographyand solid-statephysics,which
deal with three-dimensional periodic structures. To generalize to
N dimensions,
we first consider a special case in which an N-dimensional periodic function is a
productof N one-dimensional periodic functions. That is, we take the N functions
f(J)(x)
=
~
f:
ff
iJe
2i
" kx/Lj , j =
1,2,
...
,
N,
yLj
k=-oo
and multiply them on both sides to obtain
(8.15)
where we have used the following new notations:
F(r)
ea
f(l)(xj)f(2)(X2)"
.j<N)(XN),
k",(kl,k2,
...
.k»).
gk= 2re
(kilL!,
...
,
kNILN),
V=LI
L2···
LN,
Fk sa fkl
...
fkN'
r =
(Xl,
X2,
...
,
XN).
We take Equation (8.15) as the definition
of
the Fourier series for
any
periodic
function of N variables (not
just
the product of N functions of a single variable).
However, application
of
(8.15) requires some clarification.
In
one dimension, the

208
8.
FOURIER
ANALYSIS
shape
of
the smallest region
of
periodicity is unique.
I!
is simply a liue segment
of
length
L,
for example. In two and more dimensious, however, such regions
may
havea
variety
of
shapes.
For
instance,
in twodimensions, theycanbe
rectangles,
peutagons, hexagons, and so forth. Thus, we let V in Equation (8.15) stand for
a primitive cell
of
the N-dimensional lattice. This cell is important iu solid-state
Wigner-Seitz
cell
physics, and (iu three dimeusions) is called the Wigner-Seitz cell.
I!
is customary to absorb the factor 1!.,fV iuto Fk, and write
F(r)
= L Fk
eig
k"
k
(8.16)
where the integral is over a siugle Wigner-Seitz cell.
Recall that
F(r)
is a periodic function
ofr.
Thismeans that when r is changed
by R, where R is a vector describiug the boundaries
of
a cell, then we should
get the same function:
F(r
+R) =
F(r).
When
substituted iu (8.16), this yields
F(r
+R) =
Lk
Fkeig•.
(,+R)
=
Lk
e
ig
•.
R
Fkeig•." which is equal to
F(r)
if
(8.17)
In three dimensions R =
mI8t
+ m28z +
m3a3,
where
mI,
mz.
and
m3 are
iutegers and 31, 3Z, and 33 are crystal axes, which are not generally orthogonal.
On the other hand, gk
=
nlbl
+nzhz +
n3b3,
where nl, nz, and n3are iutegers,
reciprocallallice
and
bl,
bz, and b3 are the
reclprocal
lattice
vectors
defined by
vectors
The
reader may verify that bi . 3j =
2:n:
8ij.Thus
~.
R =
(tnibi)
.
(tmj3j)
=
~nimjbi'
3j
1=1
1=1
I,l
3
=
2:n:
Lmjnj
= 2:n:(iuteger),
j=l
and Equation (8.17) is satisfied.
8.2 The FourierTransform
The Fourierseries representation
of
F
(x)
is valid for the entire
realliue
as long as
F(x)
is periodic. However, most functions encountered in physical applications
are defined in some iuterval
(a, b) withoutrepetitionbeyondthatiuterval.
I!
wonld
be useful
if
we conldalso expand such functions iu some form
of
Fourier"series."
One
way to do this is to star! with the periodic series and then
let
the period
go to iufinity while extending the domain
of
the definition
of
the function. As a

8.2 THE
FOURIER
TRANSFORM
209
f(x)
a
(a)
L
)1001
b=a+L
a-L
a
(b)
a+L
a+2L
(8.18)
(8.19)
Figure
8.4
(a) The function we want to represent. (b) The Fourierseries representation
of the
function.
specific case, suppose we are iuterested in representiug a function
f(x)
that is
defined only for the interval
(a, b) and is assigned the value zero everywhere else
[see Figure 8.4(a)]. To begiu with, we might
try
the Fourier series representation,
but this will produce a repetition of our function. This situation is depicted iu
Figure 8.4(b).
Next we may
try
a function gA
(x)
defined in the interval (a - A/2, b +A/2),
where A is an arbitrary positive number:
{
o
if
a -
A/2
< x < a,
gA(X)=
f(x)
if
a-c
x -c b,
o if b < x < b +A/2.
This function, which is depicted iu Figure 8.5, has the Fourierseries representation
I
00
gA(X)
= L gA,ne2hmxI(L+Al,
.,jL +A
n=-oo
where
I l
b
+
A/2
.
gA.n =
e-2l1rnxI(L+AlgA(X)dx.
.,jL +A
a-A/2
We have managed to separate various copies of the original periodic function
by A.
It
should be clear that
if
A
--->
00,
we can completely isolate the function

210
8.
FOURIER
ANALYSIS
and
stop the repetition.
Let
us investigate the behavior
of
Equations (8.18) and
(8.19) as A grows without bound. First, we notice that the quantity
k
n
defined by
k
n
es
2n71:
/
(L
+A)
and
appearing in the exponent becomes almost continuous.
In other words, as n changes by
one
unit, k
n
changes only slightly. This suggests
that the terms in the sum in Equation (8.18) can be
lumped
together in j intervals
of
width
Sn
j , giving
where
kj
ea
2nj7l:/(L
+A),
and
gA(kj)
==
gA,nj'
Substituting !'1nj =
[(L
+
A)
/271:]!'1k
j in the above sum, we obtain
where we introduced
gA(kj)
defined by
gA(kj)
sa
.J(L
+A)/271:
gA(k
j).
It
is
now clearthatthe preceding sum approaches an integral in the limitthat
A --+
00.
Fourier
integral
In the same limit, gA
(x)
--+
f
(x),
and
we have
transforms
f(x)
=
~1°O
f(k)eikXdk,
'V
21l'
-00
where
(8.20)
(8.21)
- . - .
JL+A
f(k)
sa
lim
u(kj)
=
lun
--
gA(kj)
A--+oo
A-+oo
2n
JL +A I
lb+
Af
2 .
=
lim
e-'kjXgA(x)dx
A....
oo
271:.JL
+A
a-A/2
=
_1_1
00
f(x)e-ikxdx.
...J2ir
-00
Equations (8.20) and (8.21) are called the
Fourier
integral
transforms
of
f(k)
and
f(x),
respectively.
8.2.1,
Example.
Letus evaluatethe Fouriertransformof thefunctiondefiuedby
f(x)
= {b
if
Ixl
< a,
D if
[x]
> a
(seeFigure 8.6).From (8.21)we bave
J(k)
=
_1_
foo
f(x)e-ikxdx
=
_b_
fa
e-ikxdx
= 2ab
(Siuka),
."fiii
-00
."fiii
-a
."fiii ka
whichis the
function
encountered
(and
depicted)
in
Example
6.1.2.

a-N2
8.2
THE
FOURIER
TRANSFORM
211
b+N2
Figure 8.5 By
introducing
the
parameter
A, we have
managed
to
separate
thecopiesof the
function.
Letusdiscussthisresultin
detail.
First,
notethat
if
a
~
00,
the
function
f (x) becomes
a
constant
function
overthe
entire
real line, andwe get
_ 2b
sinka
2b
I(k)
= = lim
--
=
=7C8(k)
v
21r
e-e-oc k '"
21r
by theresultof
Example
6.1.2.This is the
Fourier
transformof an
everywhere-constant
function
(see
Problem
8.12).Next,letb --+
00
anda --+0 in suchawaythat2ab, whichis
the area under
I(x),
is
I.
Then
I(x)
will approach the delta function, and
j(k)
becomes
_ 2ab
sinka
I
sinka
I
I(k)
= lim
---
=- lim
--
=
-.
b....
oo.j'iii
ka
.j'iii
a
....
O ka
.j'iii
a-+O
Heisenberg
uncertainty
relalion
So theFouriertransform ofthe deltafunctionis the constant
1/~.
Finally, we note that the width
of
I(x)
is
Sx
=2a, and the width
of
j(k)
is roughly
the
distance,
onthek-axis,betweenits
first
two
roots,
k+ and
k_.
on
either
sideof k = 0:
t>k =k+
-k_
=
27C
[a. Thus increasingthe width
of
I(x)
resultsin a decrease in the width
of
!(k).
In
other
words,
whenthe
function
is wide, its
Fourier
transform
is
narrow.
In the
limit
of
infinite width(a constantfunction), we getinfinite
sharpness
(thedelta
function).
Thelasttwo
statements
are
very
general.
In fact,it canbe shownthatAxAk
~
1forany
function I (x). When both sides
of
this inequality are multiplied by the (reduced) Planck
constant
a
==
h/(23t}, theresultisthe
celebrated
Heisenberguncertaintyrelation:
3
t>xt>p 2: Ii,
where p = Ilk is the momeutum
of
the particle. Having obtainedthe transform
of
I(x),
we
canwrite
I(
I 1
00
2b
sinka
ikxdk
_ b 1
00
sinka
ikxdk
x}=--
----e
--
--e
.
.j'iii
-oo.j'iii
k
7C
-00
k
III
3Inthecontextof the
uncertainty
relation,
thewidthof thefunction-the so-calledwavepacket-measures the
uncertainty
inthe
position
x of a
quantum
mechanical
particle.
Similarly,
thewidthof the
Fourier
transform
measures
the
uncertainty
ink,
whichis
related
to
momentum
p via p = hk,
212
B.
FOURIER
ANALYSIS
f(x)
b
ax
_a
a
x
Figure8.6 The square"bump" function.
8.2.2.
Example.
Let us evaluatethe
Fourier
transform of a Gaussian
g(x)
=
ae-
bx2
witha,b
> 0:
a 1
00
2
ae-
k2
/
4b
1
00
2
g(k) =
--
e-b(x +ikxjb)dx =
e-
b(x+ikj2b)
dx .
../2ii
-00
../2ii
-00
To
evaluate
this
integral
rigorously,
we
would
havetouse
techniques
developed incomplex
analysis,
whicharenot
introduced
until
Chapter
10(see
Example
10.3.8).
However,
wecan
ignore
thefact
that
the
exponent
is
complex,
substitute
y = x +
ik/(2b),
andwrite
1
00
e-b[x+ik/(2b)]2
dx = 1
00
e-by2
dy =
E,
-00 -00
Vb
Thus, we haveg(k) =
::"'e-
k'j(4b),
which is also a Gaussian.
-n»
We note again that the width of
g(x),
which is proportional to
lj../b,
is in inverse
relationto the widthof
g(k), whichis proportionalto
../b.
Wethus have AxAk - 1.
III
Equations (8.20) and (8.21) are reciprocals
of
one another. However, it is
not
obvious that they are consistent.
In
otherwords,
if
we substitute(8.20) in the
RHS
of
(8.21), do we
get
an identity?
Let's
try this:
Ilk)
=
_1_1
00
dx
e-
ikx
[_1_1
00
!(k')eik'Xdk']
..;z;r
-00
..;z;r
-00
=
~
1
00
dx
1
00
!(k')ei(k'-k)Xdk'.
21l'
-00 -00
We
now
change
the
order
of
the two integrations:
Ilk)
= 1
00
dk' /(k')
[~1°O
dx
ei(k'-k)X] .
-00
21t
-00
But
the
expressionin
the
square brackets is
the
deltafunction (see Example6.1.2).
Thus, we have
Ilk)
=
J~oo
dk'
!(k')8(k'
- k),
which
is an identity.
