Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


5.2
THE
SPACE
OF
SQUARE-INTEGRABLE
FUNCTIONS
151
space
of
functions
becomes
complete. An
important
class
of
functions has already
been
mentioned
in
Chapter
I.
These
functions satisfy the
inner
product
given
by
square-integrable
functions
(gl
f)
= l
b
g*(x)!(x)w(x)
dx.
If
g(x)
= f
ix),
we obtain
(fl
f)
= l
b
1!(x)1
2w(x)
dx.
(5.6)
Functions
for
which
such
an integral is defined are
said
to be
square-integrable.
David Hilbert (1862-1943), the greatest mathematician of this
century,
receivedhis Ph.D.fromthe University of
Konigsberg
and was a member of the staffthere from 1886to 1895.ln 1895
he was
appointed
to the
chair
of
mathematics
attheUniversity
of
Gottingen, wherehe
continued
to teachfortherestofhislife.
Hilbert
is one of
that
rare
breedof late
19th-century
math-
ematicians
whose
spectrum
of
expertise
covereda wide
range,
with
formal
set
theory
atoneendand
mathematical
physicsatthe
other.Hedid superbworkingeometry,algebraicgeometry,alge-
braic
number
theory,
integral
equations,
and
operator
theory.
The
seminaltwo-volume bookMethodender mathematische Physik
by
R.
Courant,
stilloneofthebestbooksonthe
subject,
was
greatly
influenced
by
Hilbert.
Hilbert's
work
in
geometry
hadthe
greatest
influence
in
that
area
since
Euclid.
A
system-
atic
study
ofthe
axioms
of
Euclidean
geometry
led
Hilbert
to
propose
21 such
axioms,
and
he analyzed their significance. He published Grundlagen der Geometrie in 1899,puttiug
geometry
onaformal
axiomatic
foundation.
His
famous
23
Paris
problems
challenged
(and
stilltoday
challenge)
mathematicians
to solve
fundamental
questions.
It
waslateinhis
career
that
Hilbert
turned
to the
subject
forwhichheis most
famous
among
physicists. A
lecture
by Erik
Holmgren
in 1901 on
Fredholm's
work
on
integral
equations,
whichhadalready been
published
in
Sweden,
aroused
Hilbert's
interest
in the
subject.
David
Hilbert,
having
established
himselfasthe
leading
mathematician
ofhis time
byhis
work
on
algebraic
numbers,
algebraic
invariants,
andthe
foundations
of
geometry,
now
turned
his
attention
tointegralequations.Hesays
that
an
investigation
ofthe
subject
showed
him
that
itwas
important
forthe
theory
of
definite
integrals,
forthe
development
of
arbitrary
functions
in
series
(ofspecial
functions
or
trigonometric
functions).
forthe
theory
of
linear
differential
equations,
for
potential
theory.
andforthe
calculus
of
variations.
He
wrote
a
series
of six
papers
from
1904to 1910and
reproduced
them
inhisbookGrundzuge
einerallgemeinenTheone der linearenIntegralgleichungen (1912).
During
the
latter
part
of thisworkhe
applied
integral
equations
to
problems
of
mathematical
physics.
Itis said
that
Hilbert
discovered
the
correct
field
equation
for
general
relativity
in 1915
(one
year
before
Einstein)
usingthe
variational
principle,
but
never
claimed
priority.
Hilbert claimed that he workedbest out-of-doors.He accordingly attached an 18-foot
blackboard
tohis
neighbor's
wallandbuilta
covered
walkway
there
so
that
hecould
work
outside
in any
weather.
He would
intermittently
interrupt
his
pacing
andhis
blackboard

152
5. HILBERT
SPACES
computations
witha few
turns
around
therestof theyardonhis bicycle,orhewouldpull
someweeds,ordo some
garden
trimming.
Once,whenavisitorcalled,themaidsenthim
to the
backyard
and
advised
thatif the
master
wasn't
readily
visible atthe
blackboard
to
lookforhimup
in oneof the
trees.
Highlygiftedandhighlyversatile, David
Hilbert
radiated
over
mathematics
a
catching
optimism
anda
stimulating
vitality
that
canonlybecalled"the
spirit
of
Hilbert,"
Engraved
on a stone
marker
set over
Hilbert's
grave
in Gottingen arethe
master's
own
optimistic
words:
"WiT
mussenwissen.
WiT
werden
wissen."
("We
must
know.
Weshall
know.")
The space of square-integrable functions over the interval [a, b] is denoted by
.c~(a,
b). In this notation L stands for Lebesgue, who generalized the notion of
the ordinary Riemann integral to cases for which the integrand could
be highly
discontinuous; 2 stands for the power
of
j
(x)
in the integral; a and b denote the
limits
of
integration; and w refers to the weight function (a strictly positive real-
valued function). When
w(x)
= I, we use the notation .c
2
(a, b). The significance
of
.c~(a,
b) lies in the following theorem (for a proof, see [Reed 80, ChapterIII]):
£'~(a,
b)
is
complete
5.2.1.
Theorem.
(Riesz-Fischer theorem) The space
.c~(a,
b) is complete.
A complete infinite-dimensional ioner product space was earlier defined to be
a Hilbert space. The following theorem shows that the number of Hilbert spaces
is severely restricted. (For a proof, see [Frie 82, p. 216].)
all
Hilbert
spacesare
alike
5.2.2.
Theorem.
All infinite-dimensional complete inner product spaces are iso-
morphic to
.c~(a,
b).
.c~
(a, b) isdefined in terms
of
functions that satisfyEquation(5.6). Yetanioner
product involves integrals of the form
J:
g*(x)j(x)w(x)
dx: Are such integrals
well-defined and finite? Using the Schwarz inequality, which holds for any ioner
product space, finite or infinite, one
can
show that the integral is defined. The
isomorphism
of
Theorem 5.2.2 makes the Hilbert space more tangible, because it
identifies the space with a space
of
functions, objects that are more familiar than
abstract vectors. Nonetheless, a faceless function is very little improvement over
an abstract vector. What is desirable is a set
of
concrete functions with which we
can calculate. The following theorem provides such functions (for a proof, see
[Sinon 83, pp. 154-161]).
5.2.3.
Theorem.
(Stone-Weierstrass approximation theorem) The sequence
oj
functions (monomials) {x
k
},
where k = 0,
1,2,
...
.forms a basis
oj
.c~(a,
b).
Thus, any function j can be written as
j(x)
=
L:~oakxk.
Note that the
{x
k
}
are not orthonormal but are linearly independent.
If
we wish to obtain an
orthononnal-or
simply
orthogonal-linear
combination
of
these vectors, we can
use the Gram-Schmidtprocess. The result will be certainpolynomials, denoted by
Cn(x), that are orthogonal to one another and span
.c~(a,
b).

5.2 THE
SPACE
OF
SQUARE-INTEGRABLE
FUNCTIONS
153
Such orthogonal polynomials satisfy very useful
recurrence
relations, which
we now derive.
In the following discussion
P,k(X)
denotes a generic polynomial
of
degree less than or equal to k. For example, 3x
s
-
4x
2
+5, 2x +I,
-2.4x
4
+
3x
3
-
x
2
+6, and 2 are all denoted by
p,s(x)
or
p,s(x)
or p,S9(X) because they
all have degrees less than or equal to 5, 8, and 59. Since a polynomial of degree
less than
n can be written as a liuear combination
of
Ck(X) with k < n, we have
the obvious property
1
b
Cn(x)P,n_l(x)w(x)dx
=
O.
(5.7)
Let k
m
and
k~
denote, respectively, the coefficients of x
m
andx
m
-
1
in Cm(x),
and let
h
m
=
1b[Cm(x)fw(X)dX.
(5.8)
The polynomial
CnH
(x) -
(knHI
kn)xCn(x)
has degree less than or equal to n,
and therefore can be expanded as a linear combination
of
the Cj (x):
(5.9)
form
:On-2.
form:On-2.
Take the inner product
of
both sides of this equation with Cm(x):
1
b
~+11b
Cn+l(x)Cm(x)w(x)dx
-
--
xCn(x)Cm(x)w(x)dx
a k
n
a
n (b
=
I:aj
I,
Cj(x)Cm(x)w(x)
dx.
j=O a
The first integral on the LHS vanishes as long as m :0 n; the second integral
vanishes if
m :0 n - 2 [if m :0 n - 2, then
xCm(x)
is a polynomial of degree
n - 1]. Thus, we have
n r
I:aj
I,
Cj(x)Cm(x)w(x)dx
= 0
j=O
a
The integral in the sum is zero unless j = m, by orthogonality. Therefore, the sum
reduces to
am1
b
[C
m(x)]2
W(x)
dx
= 0
Sincethe
integral
is
nonzero,
weconclude
that
am
= 0 form =0, 1,2,
...
,n - 2,
and Equation (5.9) reduces to
k
n
+!
Cn+l(X) -
--xCn(x)
=
an-lCn-!(X)
+anCn(x).
(5.10)
k
n

154
5. HI
LBERT
SPACES
It
can be shown that
if
we define
k
n+l
an =
--,
k
n
s; an
Yn=-----,
hn-l
an-l
(5.11)
a
recurrence
relation
then Equation (5.10) can be expressed as
lor
orthogonal
polynomials
C
n+l(X)
=
(anx
+f3n)C
n(x)
+Vn
Cn-l(X),
or
(5.12)
(5.13)
Other recurrence relations, involving higher powers
of
x,
can be obtained from
the
one
above. For example, a recurrence relation involving x
2
can be obtained
by multiplying bothsides
of
Equation (5.13) by x and expanding each term
of
the
RHS using that same equation.
The
result will be
(5.14)
5.2.4. Example. Asan
application
of
the
recurrence
relations
above,
letus
evaluate
t,
==
l
b
xCm(x)Cn(x)w(x)dx.
Substituting (5.13)in the integralgives
1 l
b
P l
b
lj
=- C
m(x)C
n+l(x)w(x)dx
- --"
Cm(x)Cn(x)w(x)dx
an a an a
~
l
b
- --" Cm(X)Cn_l
(x)w(x)
dx.
IXn a
Wenowuse the
orthogonality
relations
among
theCk(X) to
obtain
1 l
b
.
P l
b
lj
=
~8m,n+l
C~(x)w(x)dx---"8mn
C~(x)w(x)dx
an a an a
Yn l
b
2
-
-8
m,n-l
Cm(x)w(x)dx
IXn a
(
1 8 Pm Ym+l )
=
--
m,n+l -
-8
mn
-
--8
m
,n- l h
m•
Clm-l
am
Cl
m+l

5.2
THE
SPACE
OF
SQUARE-INTEGRABLE
FUNCTIONS
155
or
III
if
m = n +
I,
if
m = n,
j
hml
Ol
m
_
1
I
-{3mhm/am
1-
-0Ym+l
hm/
am+l
if m = n - 1,
otherwise.
5.2.5. Example. Letus findtheorthogonalpolynomialsformingabasisof £.2
(-I,
+I),
whichwedenoteby Pk(X), wherek isthe degreeof thepolynomial.Let Po(x) =L Tofind
PI (x), writePI (x) = ax
+b,
anddeterminea andb in suchawaythatPI (x) isorthogonal
to
Po(x):
0=1
1
PI (x) Po(x) dx
= 1
1
(ax +b)
dx
=
!ax21~1
+2b = 2b.
-I
-I
So oneof the
coefficients,
b, is
zero.
To
find
the
other
one;
weneedsome
standardization
procedure.We"standardize"Pk(X) by requiringthat
Pk(l)
= I Vk: For k = I this yields
a x 1 =
I,ora
= 1.so that PI
(x)
=X.
WecancalculateP2(X) similarly:Write P2(X) =ax
2
+bx +c, imposethe condition
that it be orthogonalto both
PI (x) and Po(x), and enforcethe standardizationprocedure.
All this will yield
1
1 2 1
1
2
0=
P2(x) Po(x)
dx
=
-a
+2c, 0 = P2(x) PI (x)
dx
=
-b,
-I
3
-I
3
andP2(1) =
a+b+c
= L Thesethreeequationshavetheuniquesolutiona =
3/2,
b = 0,
c
=
-1/2.
Thus, P2(X) =
!(3x
2
-
I). These are the first threeLegendrepolynomials,
which
are
part
of a
larger
group
of
polynomials
tobediscussed in
Chapter
7. II
5.2.1 Orthogonal Polynomials and Least Squares
The
method
of
least squares is no doubt familiar to the reader. In the simplest
procedure,
one
tries to find a linear function that
most
closely fits a set
of
data.
By defioition,
"most
closely" means thatthe sum
of
the squares
of
the differences
between the data points and the corresponding values
of
the linear function is
minimum. More generally, one seeks the best polynomial fit to the data.
We shallconsidera relatedtopic, namelyleast-squarefitting
of
a givenfunction
withpolynomials. Suppose
f(x)
is a function defined on (a, b).We
wantto
find a
polynomialthatmost closelyapproximates
f.
Write sucha polynomial as
p(x)
=
L:Z=o
akx
k,
where the
ak's
are to be determined such that
S(ao,
011,
...
, an) ea l
b
[f(x)
-
010
-
alx
-
...
- a
nx
n]2
dx
is a minimum. Differentiating S withrespectto the
ak's
and
setting the resultequal
to zerogives
as
l
b
[
n ]
0=-.
=
2(-x
i
)
f(x)
-
I>kXk
dx,
oa
J
a k=O

158 5. HILBERT
SPACES
(a) II! ±
gil
= II!II+
IIgll·
(b) II! +
gll2
+II! -
gll2
=
2(1If11
+
IIgll)2.
(c) Using parts (a), (b), and
Theorem
1.2.8, show that .c1(R) is
not
an inner
product space. This shows that
not
all norms arise from an inner product.
5.6.
Use
Equation (5.10) to derive Equation (5.12). Hint: To find an, equate the
coefficients
of
x" on both sides
of
Equation (5.10). To find
an-I,
multiply
both
sides
of
Equation (5.10) by Cn_IW(X) and integrate, using the definitions
of
k
n,
k~,
andhno
5.7. Evaluate the integral
f:
x
2C
m
(x)C
n
(x)w(x)
dx.
Additional Reading
1. Boccara, N. Functional Analysis, Academic Press, 1990. An application
oriented book with many abstract topics related to Hilbert spaces (e.g.,
Lebesgue measure) explained for a physics audience.
2. DeVito, C.
Functional Analysis and Linear Operator Theory, Addison-
Wesley, 1990.
3. Reed, M., and Simon,
B.FunctionalAnalysis, AcademicPress, 1980. Coau-
thoredby a mathematicalphysicist (B.S.), this first volume
of
a four-volume
encyclopedic treatise on functional analysis and Hilbert spaces bas many
examples and problems to help the reader comprehend the rather abstract
presentation.
4. Zeidler, E.
Applied Functional Analysis, Springer-Verlag, 1995. Another
application-oriented
book
on Hilbertspaces suitablefor a physics audience.

6,
_
Generalized Functions
Once we allow the number
of
dimensions to be infinite, we open the door for
numerous possibilities that are not present in the finite case. One such possibility
arises because
of
the variety
of
infinities. Wehave encounteredtwo types of infinity
in Chapter 0, the countable infinity and the uncountable infinity.The paradigm of
the former is the "number" of integers, and that
of
the latter is the "number" of
real numbers. The nature of dimensionality of the vector space is reflected in the
components of a general vector, which has a finite number
of
components in a
finite-dimensional vector space, a countably infinite number
of
components in
an infinite-dimensional vector space with a
countable basis, and an uncountably
infinite number of components in an infinite-dimensional vector space with no
countable basis.
6.1 ContinuousIndex
To gain an understanding
of
the nature of, and differences between, the three
types of vector spaces mentioned above, it is convenient to
think of components
as functions
of
a "counting set." Thus, the components
Ji
of
a vector If) in an
N-dimensional vector space can be thought
of
as values
of
a function f defined
on the finite set {I, 2,
...
, N}, and to emphasize such functional dependence, we
write
f
(I)
instead of
fi-
Similarly, the components
Ji
of a vector I
f)
in a Hilbert
space with the countable basis
B =
(lei)}~l
can be thought of as values
of
a
function
f : N
-->
C, where N is the (infinite) set of natural numbers. The next
step is to allow the counting set to be uncountable, i.e., a continuum such as the
real numbers or an interval thereof. This leads to a "component"
of
the form f (x)
corresponding to a function f : lR --> C. What about the vectors themselves?
What sort
of
a basis gives rise to such components?

160 6.
GENERALIZED
FUNCTIONS
Because of the isomorphism of Theorem 5.2.2, we shall concentrate on
.c~
(a, b). In keeping with our earlier notation, let {lex)
lxeJR
denote the elements
of an orthonormalset and interpret
f(x)
as (ex I
f).
The innerproductof
.c~(a,
b)
cannowbe
written
as
(glf)
=l
b
g*(x)f(x)w(x)dx
= l
b
(glex)(exl
f)
w(x)dx
= (gl
([
lex)
w(x)
(exI
dX)
i».
The lastline suggests writing
l
b
lex)
w(x)
(exI
dx
= 1.
In the physics literature the
"e"
is ignored, and one writes Ix) for lex). Hence, we
obtain
thecompleteness
relation
fora
continuous
index:
completeness
relation
fora
continuous
index
l
b
[x)
w(x)
(xl
dx
= 1,
or
l
b
[x) (xl
dx
= 1,
(6.1)
where in the secoud integral,
w(x)
is set equal to unity. We also have
If)
=
(l
b
Ix)
w(x)
(xl
dx
)
If)
=l
b
f(x)w(x)
[x)
dx,
(6.2)
which shows how to expand a vector
If)
in terms
of
the Ix)'s.
Take the inner product of (6.2) with (x']:
(xii
f)
=
f(x
')
= l
b
f(x)w(x)
(xii x)
dx
where
x'
is assumed to lie in the interval (a, b), otherwise
f(x
')
= 0 by definition.
This equation, which holds for arbitrary
f,
tells us inuuediately that
w(x)
(xii x)
is no ordinary function of
x and x'.
For
instance, suppose
f(x
')
=
O.
Then, the
result of integrationis always zero, regardless of the behavior of
f at other points.
Clearly, there is an infinitude
of
functions that vanish at x',yet all
of
them give the
same integral! Pursuing this line of argument more quantitatively, one can show
that
w(x)
(x'] x) =
Oifx
oF
x',
w(x)
(xl x) =
00,
w(x)
(x']
x) is anevenfunctiou
of x -
x',
and
J:
w(x) (x'] x)
dx
= 1. The proofis left as a problem. The reader
Dirac
delta
function
may recognize this as the
Dirac
delta
function
8(x -
x')
=
w(x)
(x'] x) , (6.3)
which, for a function f defined on the interval (a, b), has the following property.'
l
b
f(x)8(x
_
x')
dx
=
{f(x
I
)
if
x E (a,
b),
(6.4)
a 0
ifxrt(a,b).
1Foran
elementary
discussionof theDiracdelta
function
withmanyexamplesof its application, see [Hass99].
6.1
CONTINUOUS
INDEX
161
!
!
,
_._._._._._._._.
__
._~_._._---_._._._._._._.+-
............
-
········
__
·"·
__
····j···_--_·_--------·----i···_·-
.•..........
-
,
,
. .
" ..
__
._._-_._._._.~._---_._._._._._._._._~
.._.
........
-
, '
'/;
i
----f---
_._._._.-
······1-
.j
.......
-
J
~!
,
,
_._~_
..
,
."
..
---------.""-j
..
...............
-
_.J
\
.,
.......
;
,
e-,
..........
..-
.-
~~.-
,
........
-
......._.,..
,
:
j
,
!
i
i
-0.5
o 0.5
I
1.5 2
2.5
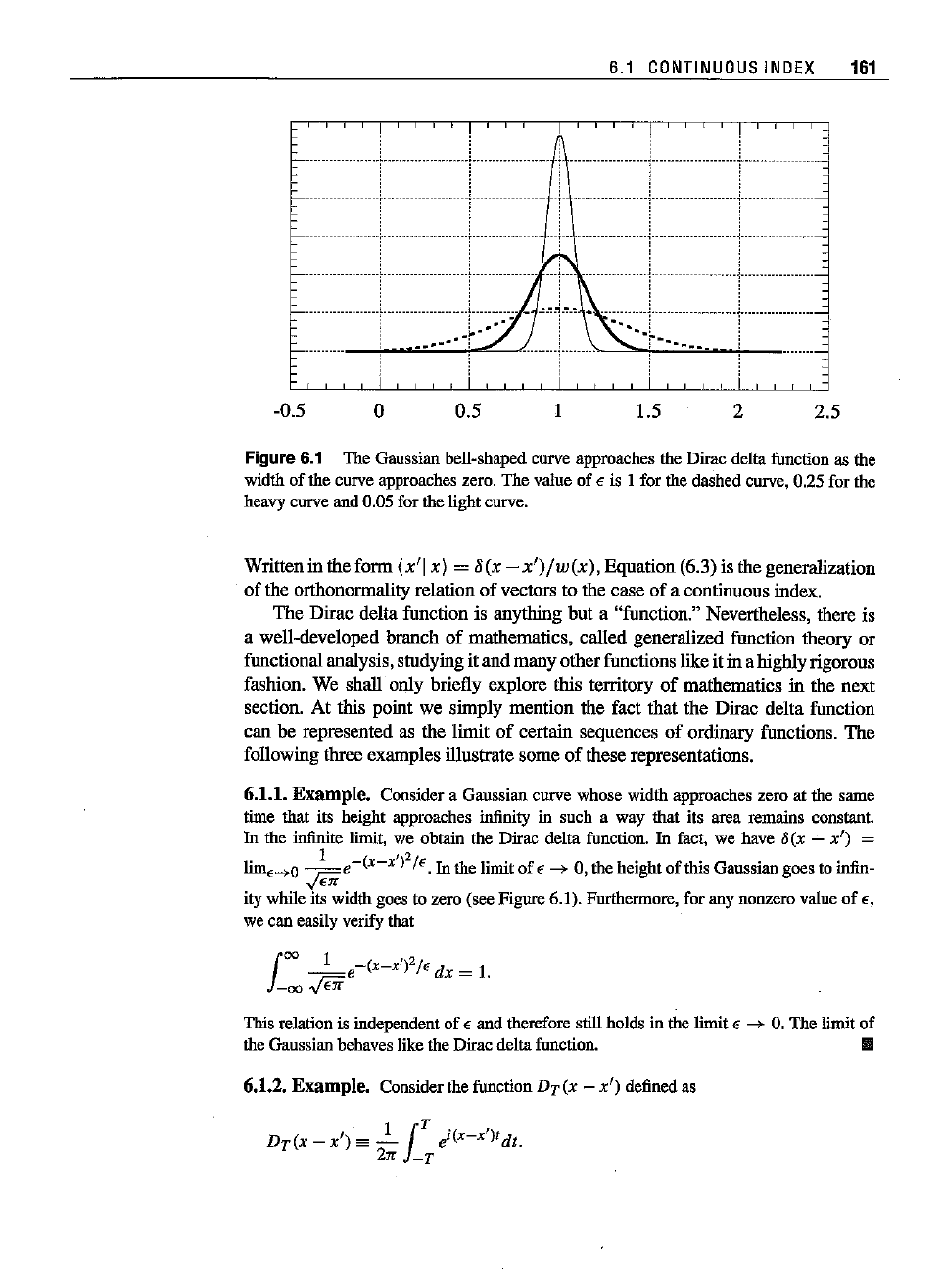
Figure 6.1 The Gaussian bell-shaped curve approaches the Dirac delta function as the
width
of
the curve approaches zero.
The
value
of
€ is 1 for the dashed curve, 0.25 for the
heavy curve and 0.05 for the light curve.
Written in the form (xii x) =
8(x
-x')fw(x),
Equation (6.3) is the generalization
of the orthonormality relation
of
vectors to the case of a continuous index.
The Dirac delta function is anything but a "function." Nevertheless, there is
a well-developed branch of mathematics, called generalized function theory or
functional analysis, studying it and many otherfunctions like it in ahighly rigorous
fashion. We shall only briefly explore this territory
of
mathematics in the next
section. At this point we simply mention the fact that the Dirac delta function
can be represented as the limit
of
certain sequences of ordinary functions. The
following three examples illustrate some of these representations.
6.1.1.Example. Consider a Gaussian curve whose width approaches zero at the same
time that its height approaches infinity
in such a way that its area remains constant.
In the infinite limit, we obtain the Dirac delta function. In fact, we have 8(x -'-
x')
=
limE-+o
~e-(X-XI)2/E.
In the limit
of
E
---+
0, the height
of
this Gaussian goes to infin-
v
H
'
ity while its width goes to zero (see Figure 6.1). Furthermore, for any nonzero value
of
E,
we can easily verify that
This relation is independent
of
E and therefore still holds in the limit E
-+
O.
The
limit
of
the Gaussian behaves like the Dirac delta function. II
6.1.2. Example.
Consider
thefunctionDT (x -
x')
defined
as
I
jT
O(
')
DT(X
-x')
==
_ e'
x-x
fdt.
2"
-T
162 6.
GENERALIZED
FUNCTIONS
-5
o 5
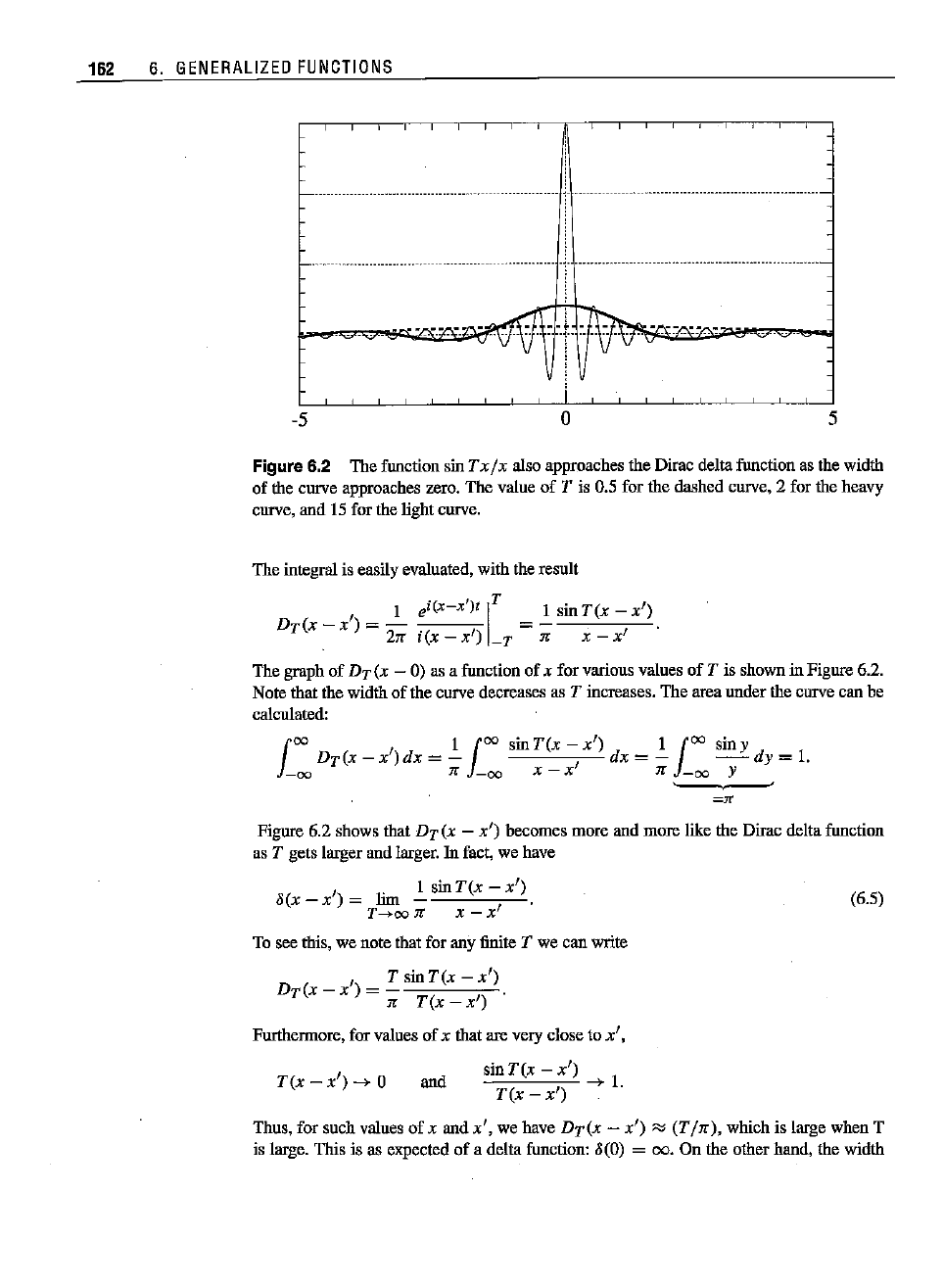
Figure 6.2 The function sin T
xf
x also approaches the Dirac delta function as the width
of the curve approaches zero.
The
value
of
T is 0.5 for the dashed curve. 2 for the heavy
curve, and 15 for the light curve.
The
integral is easily evaluated, with the result
«
')
T
1e
l
x-x
til
sinT(x
-x')
DT(X -
x')
=- = .
. 2rr
i(x
-x')
-T
7r x
-x'
The graph
of
DT(x - 0) as a function
of
x for various values
of
T is shown in Figure 6.2.
Note that the width
of
the curve decreases as T increases. The area
under
the curve can be
calculated:
1
00
, I 1
00
sin
T(x
-
x')
1 1
00
sin y
DT(X-x)dx=-
,
dx=-
--dy=l.
-00
7C
-00
X
-x
tt
-00
Y
'---'
="
(6.5)
Figure 6.2 shows that DT (x -
x')
becomes more and more like the Dirac delta function
as
T gets larger and larger. In fact, we have
~(x
_
x')
= lim I sin
T(x
-
x').
T--+oo
JC
X -
x'
and
T(x
-x')
-+ 0
To see this, we note that for any finite T we can write
DT(X _
x')
= T sin
T(x
-
x').
x
T(x
-
x')
Furthermore, for values
of
x thatare very close to
x',
sin
T(x
-
x')
I
-+ .
T(x-x')
.
Thus, for such values
of
x and
x',
we have
Dr(x
-
x')
~
(T
/Jr),
which is large when T
is large. This is as expected
of
a delta function:
~
(0) =
00.
On
the other hand, the width
