Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.

2.3 Elements of Length, Area, and Volume 61
x
y
z
'
x
'
y
e
^
x
dl
1
= dx
dl
3
= dz
dl
2
= dy
'
'
'
z
'
'
P
'
'
P
y
e
^
z
e
^
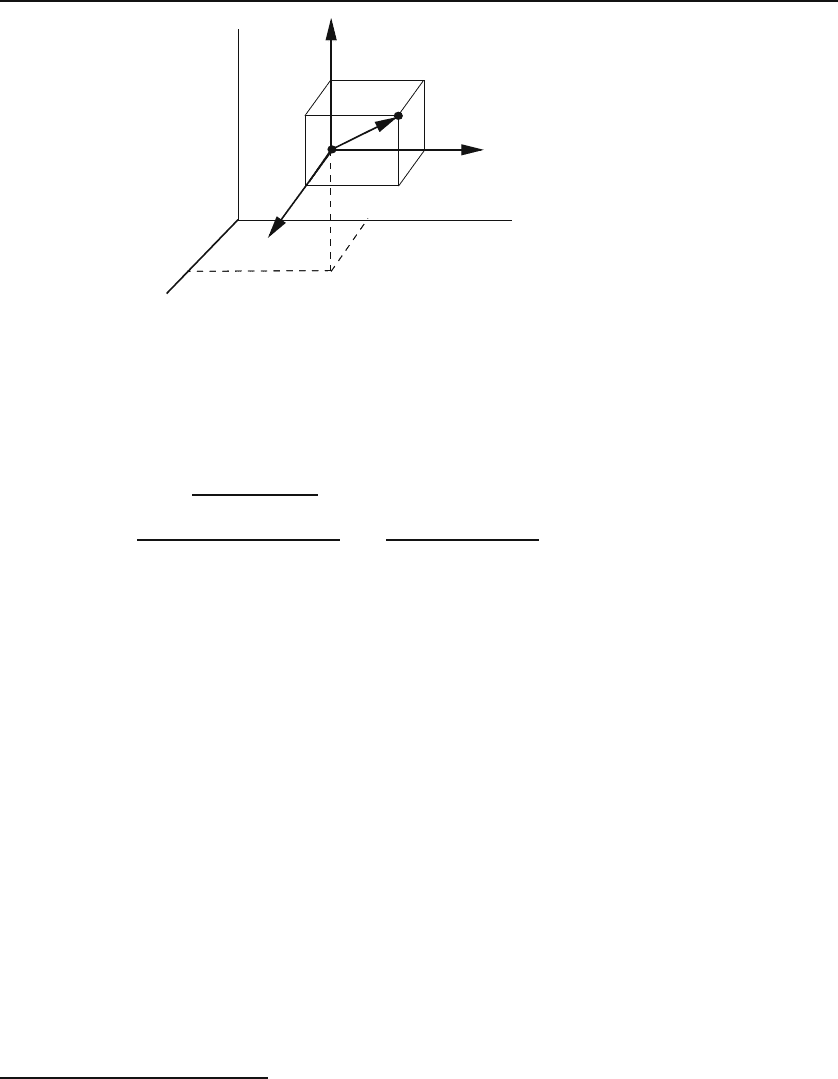
Figure 2.2: Elements of length, area, and volume in Cartesian coordinates.
includes the primary length elements as special cases: When a coordinate is
held fixed, the corresponding differential will be zero. Thus, setting dy
=0=
dz
, i.e., holding y
and z
fixed, we recover the first primary length element.
The length of d
l is also of interest:
dl ≡|d
l| =
dl
2
1
+ dl
2
2
+ dl
2
3
=
(dx
)
2
+(dy
)
2
+(dz
)
2
≡
dx
2
+ dy
2
+ dz
2
. (2.20)
In one-dimensional problems involving curves, one is either given, or has
to find, the parametric equation of a curve γ whereby the coordinates
parametric
equation of a
curve
(x
,y
,z
)ofapointonγ are expressed as functions of a parameter, usually
denoted by t. This is concisely written as
γ(t)=(x
,y
,z
) ≡
f(t),g(t),h(t)
!
,
so that the “curve function” γ takes a real number t and gives three real
numbers f (t), g(t), and h(t) which are the coordinates x
, y
,andz
of a
point on the curve in space. Usually one considers an interval
12
(a, b)forthe
real variable t.Then
f(a),g(a),h(a)
!
is the initial point of the curve and
f(b),g(b),h(b)
!
its final point. The parameter t and the functions f, g,and
h are not unique. For example, the three functions
f
1
(t)=a cos t, g
1
(t)=a sin t, h
1
(t)=0, 0 ≤ t ≤ π,
describe a semicircle in the xy-plane. However,
f
2
(t)=a cos
t
3
!
,g
2
(t)=a sin
t
3
!
,h
2
(t)=0, 0 ≤ t ≤ π
1/3
,
also describe the same semicircle. This arbitrariness is useful, because it allows
us to choose f, g,andh so that calculations become simple.
12
Do not confuse this with the coordinates of a point in the plane. The notation (a, b)
here means all the real numbers between a and b excluding a and b themselves.

62 Differentiation
For “flat” curves [lying in the xy-plane and given by an equation y = f(x)],
one obvious parameterization—which may not be the most convenient one—is
x = t, y = f (t).
Let us assume that we have chosen the three functions and they are of the
form
x
= f (t),y
= g(t),z
= h(t).
Then the primary lengths can be written as
dx
= f
(t) dt, dy
= g
(t) dt, dz
= h
(t) dt,
and the element of displacement along the curve becomes
the infinitesimal
element of
displacement
along a curve
dr
(t)=d
l(t)=
ˆ
e
x
f
(t) dt +
ˆ
e
y
g
(t) dt +
ˆ
e
z
h
(t) dt,
|dr
(t)| = dl(t)=
[f
(t) dt]
2
+[g
(t) dt]
2
+[h
(t) dt]
2
=
[f
(t)]
2
+[g
(t)]
2
+[h
(t)]
2
dt, (2.21)
where a prime on a function denotes its derivative with respect to its argu-
ment.
13
The first primary surface at P
is obtained by holding x
constant and
letting the other two coordinates vary arbitrarily. It is clear that the resulting
primary surfaces
of Cartesian
coordinates are
planes
surface is a plane passing through P
and parallel to the yz-plane. It is also
clear that the first primary length element, dx
is perpendicular to the first
primary surface. The first primary element of area, denoted by da
1
,issimply
dy
dz
. The second and third primary surfaces are the xz-plane and the xy-
plane, respectively. These planes are perpendicular to their corresponding
length elements. The primary elements of area are obtained similarly. We
thus have
primary elements
of area in
Cartesian
coordinates
da
1
= dy
dz
,da
2
= dx
dz
,da
3
= dx
dy
. (2.22)
Finally, the volume element is
element of volume
in Cartesian
coordinates
dV = dl
1
dl
2
dl
3
= dx
dy
dz
. (2.23)
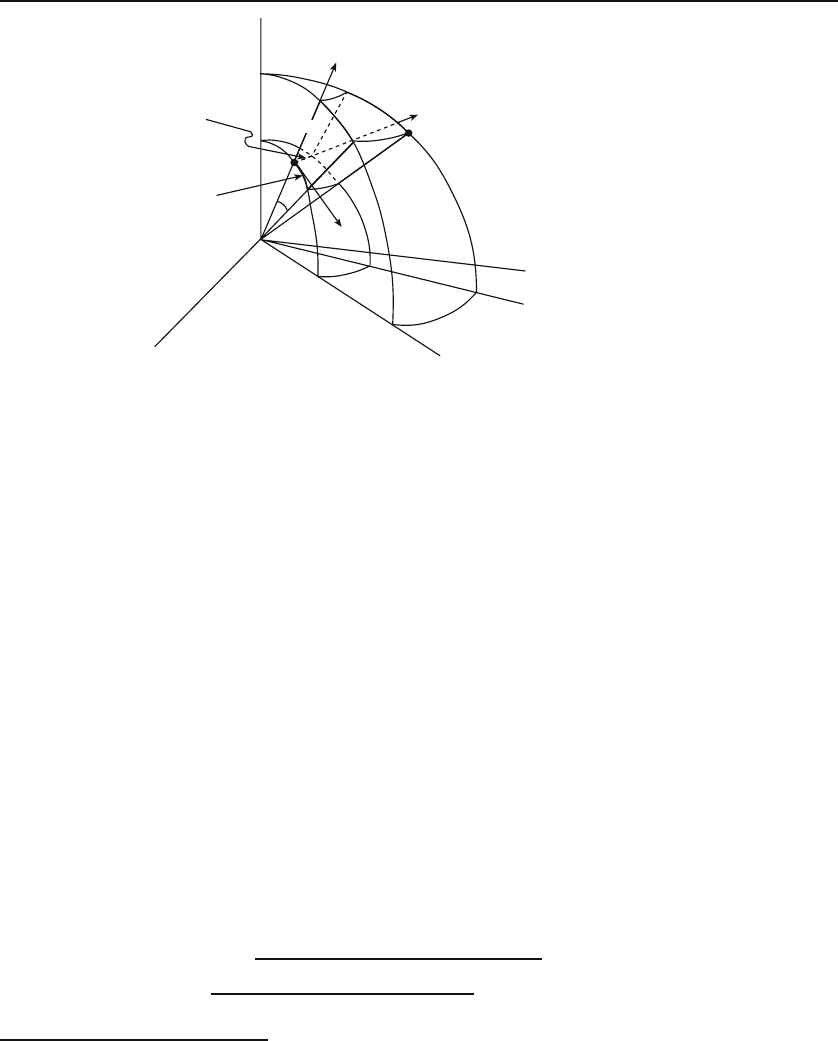
2.3.2 Elements in a Spherical Coordinate System
The point P
in Figure 2.3 now has coordinates (r
,θ
,ϕ
). To find the primary
length along
ˆ
e
r
, keep θ
and ϕ
fixed and let r
change to r
+ dr
.ThenP
will be displaced by dr
along
ˆ
e
r
. Thus, the first primary length element, dl
1
,
is simply dr
. To find the primary length along
ˆ
e
θ
, keep r
and ϕ
fixed, i.e.,
13
The use of primes to represent both the derivative and the coordinates of the element of
the source (such as dm) is unfortunately confusing. However, this practice is so widespread
that any alteration to it would result in more confusion. The context of any given problem
is usually clear enough to resolve such confusion.
2.3 Elements of Length, Area, and Volume 63
′
P
′′
P
Δ
′
ϕ
Δ
′
θ
Δ
′
r
′
r
Δ
′
θ
′
r
sin
′
θΔ
′
ϕ
x
y
z
Figure 2.3: Elements of length, area, and volume in spherical coordinates. We have
used “Δ”insteadof“d.”
confine yourself to the plane passing through P
and the polar—or z—axis,
and let θ
change to θ
+ dθ
.ThenP
will be displaced by
14
r
dθ
along
ˆ
e
θ
. The primary length along
ˆ
e
ϕ
is obtained by keeping r
and θ
fixed,
i.e., confining oneself to a plane passing through P
and perpendicular to the
z-axis,
15
and letting ϕ
change to ϕ
+ dϕ
.ThenP
will be displaced along
a circle of radius r
sin θ
by an angle dϕ
. This can be seen by noting that P
lies in the xy-plane and that its distance from the z-axis is given by
x
2
+ y
2
=(r
sin θ
cos ϕ
)
2
+(r
sin θ
sin ϕ
)
2
= r
2
sin
2
θ
and that the RHS, which is the square of the radius of the circle, is a con-
stant. The displacement of P
is therefore r
sin θ
dϕ
along
ˆ
e
ϕ
.Ageneral
infinitesimal (vector) displacement can, therefore, be written as
general spherical
infinitesimal
displacement
dr
= d
l =
ˆ
e
r
dl
1
+
ˆ
e
θ
dl
2
+
ˆ
e
ϕ
dl
3
=
ˆ
e
r
dr
+
ˆ
e
θ
r
dθ
+
ˆ
e
ϕ
r
sin θ
dϕ
. (2.24)
Note again that this vectorial infinitesimal displacement includes the primary
length elements as special cases. Thus, setting dθ
=0=dϕ
, i.e., holding θ
and ϕ
fixed, we recover the first primary length element. The length of dr
(or d
l)is do not confuse
|dr
| with dr
,they
are not equal.
|dr
| = dl =
(dr
)
2
+(r
dθ
)
2
+(r
sin θ
dϕ
)
2
=
dr
2
+ r
2
dθ
2
+ r
2
sin
2
θ
dϕ
2
. (2.25)
14
Since r
is held fixed, P
is confined to move on a circle of radius r
, describing an
infinitesimal arc subtended by the angle dθ
.
15
Fixing r
and θ
fixes z
= r
cos θ
which describes a plane parallel to the xy-plane, i.e.,
a plane perpendicular to the z-axis.
64 Differentiation
If we know the parametric equation of a curve in spherical coordinates,
i.e., if the coordinates r
,θ
,andϕ
of a point on the curve can be expressed as
functions of the parameter t, then we can find the differentials in terms of dt
and substitute in Equation (2.25) to find an expression analogous to Equation
(2.21). We leave this as an exercise for the reader.
The first primary surface at P
is obtained by holding r
constant and
letting the other two coordinates vary arbitrarily. It is clear that the resulting
primary surfaces
of spherical
coordinates
consist of a
sphere, a cone,
and a plane.
surface is a sphere of radius r
passing through P
. It is also clear that the
first primary length element dr
is perpendicular to the first primary surface.
It is not hard to convince oneself that the second and third primary surfaces
are, respectively, a cone of (half) angle θ
, and a plane containing the z-axis
and making an angle of ϕ
with the x-axis. These surfaces are perpendicular
to their corresponding length elements. The primary elements of area are
obtained easily. We simply quote the results:
primary elements
of area in spherical
coordinates
da
1
=(r
dθ
)(r
sin θ
dϕ
)=r
2
sin θ
dθ
dϕ
,
da
2
=(dr
)(r
sin θ
dϕ
)=r
sin θ
dr
dϕ
, (2.26)
da
3
=(dr
)(r
dθ
)=r
dr
dθ
.
Finally, the volume element is
element of volume
in spherical
coordinates
dV =(dr
)(r
dθ
)(r
sin θ
dϕ
)=r
2
sin θ
dr
dθ
dϕ
. (2.27)
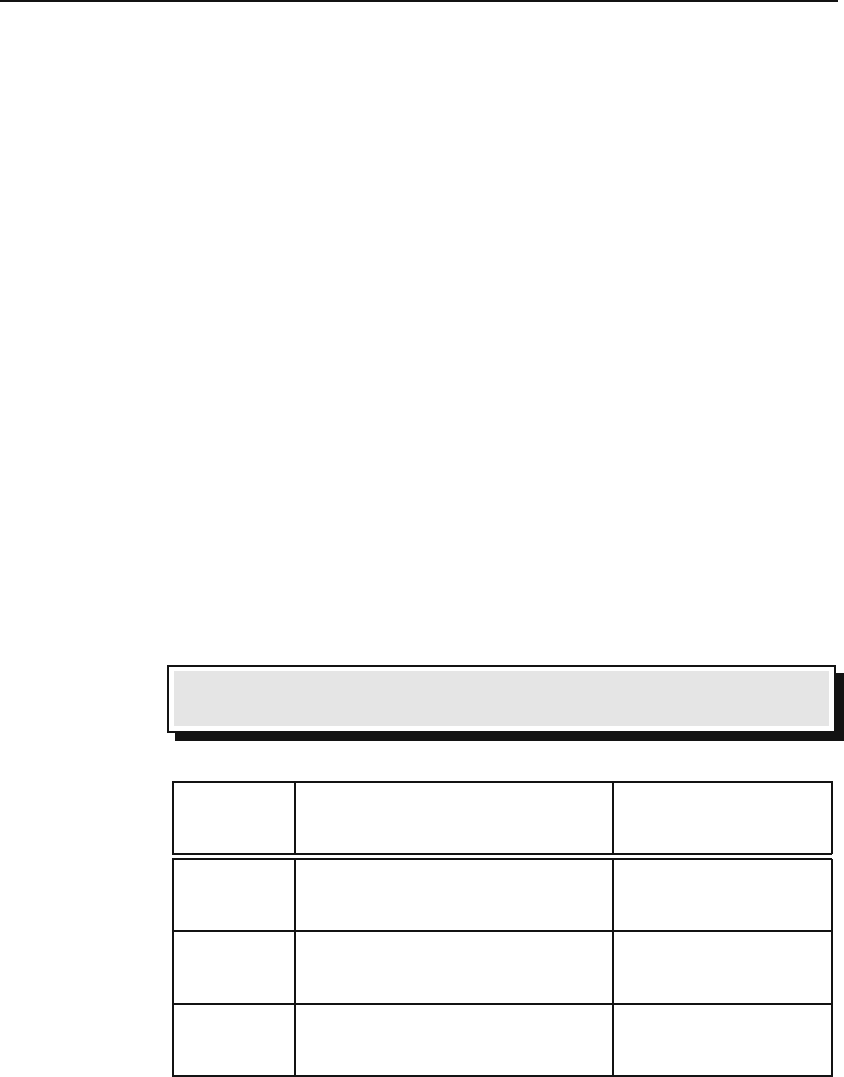
Table 2.1 gathers together all the primary curves and surfaces for the
three coordinate systems used frequently in this book. The reader is advised
to remember that
Box 2.3.3. All the differentials of Table 2.1 carry a prime to emphasize
that they are evaluated at P
, the location of infinitesimal elements.
Coordinate Primary Primary
system curves surfaces
1st: Straight line (x-axis) yz-plane
Cartesian 2nd: Straight line (y-axis) xz-plane
3rd: Straight line (z-axis) xy-plane
1st: Rays perp. to z-axis Cylinder with axis z
Cylindrical 2nd: Circle centered on z-axis Half-plane from z-axis
3rd: Straight line (z-axis) Plane perp. z-axis
1st: Rays from origin Sphere
Spherical 2nd: Half-circle Cone of half angle θ
3rd: Circle centered on polar axis Half-plane from z-axis
Table 2.1: Primary curves and surfaces of the three common coordinate systems.
2.3 Elements of Length, Area, and Volume 65
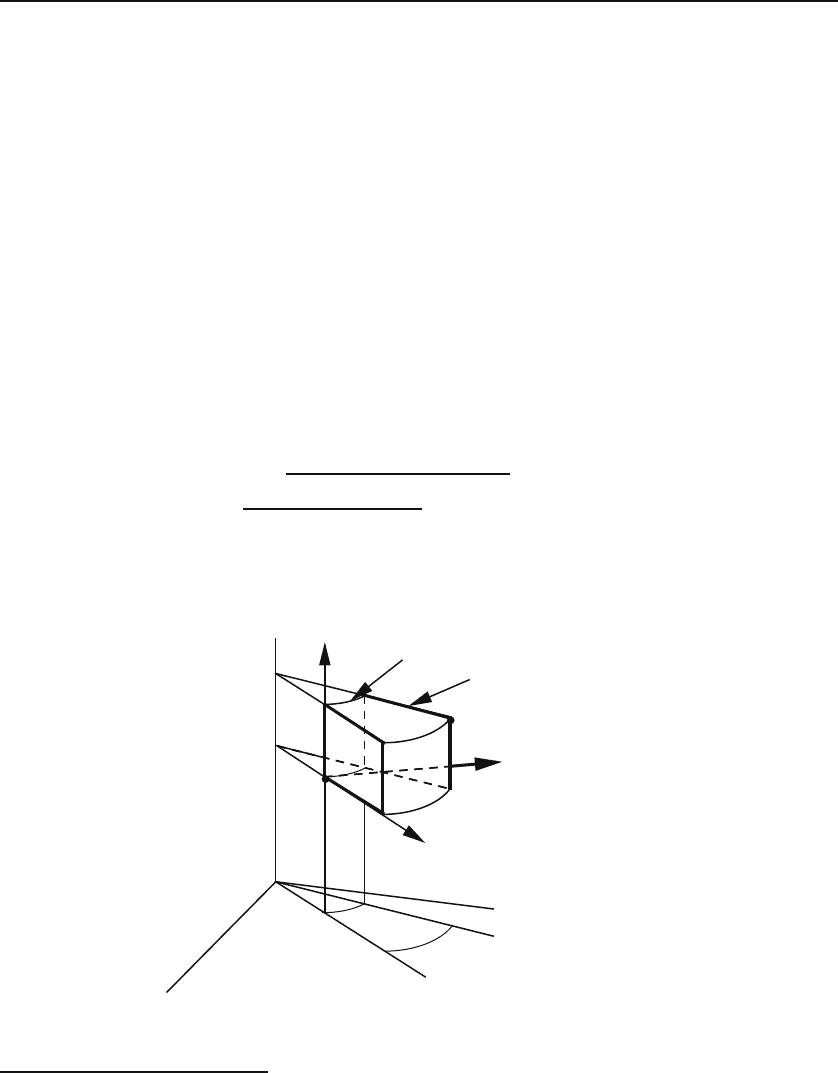
2.3.3 Elements in a Cylindrical Coordinate System
The coordinates of P
are now (ρ
,ϕ
,z
) as shown in Figure 2.4. To find the
primary length along
ˆ
e
ρ
, keep ϕ
and z
fixed and let ρ
change to ρ
+ dρ
.
Then P
will be displaced by dρ
along
ˆ
e
ρ
. Thus, the first primary length
element dl
1
is simply dρ
. To find the primary length along
ˆ
e
ϕ
, keep ρ
and z
fixed, i.e., confine yourself to a circle of radius ρ
in the plane passing through
P
and perpendicular to the z-axis, and let ϕ
change to ϕ
+ dϕ
.ThenP
will be displaced by ρ
dϕ
along
ˆ
e
ϕ
. The primary length along
ˆ
e
z
=
ˆ
e
z
is
16
obtained by keeping ρ
and ϕ
fixed, and letting z
change to z
+ dz
.Then general cylindrical
infinitesimal
displacement
P
will be displaced by dz
. A general infinitesimal (vector) displacement can,
therefore, be written as
dr
= d
l =
ˆ
e
ρ
dl
1
+
ˆ
e
ϕ
dl
2
+
ˆ
e
z
dl
3
=
ˆ
e
ρ
dρ
+
ˆ
e
ϕ
ρ
dϕ
+
ˆ
e
z
dz
. (2.28)
Note again that this infinitesimal displacement includes the primary length
elements as special cases. The length of this vector is
|dr
| = dl =
(dρ
)
2
+(ρ
dϕ
)
2
+(dz
)
2
=
dρ
2
+ ρ
2
dϕ
2
+ dz
2
. (2.29)
If we know the parametric equation of a curve in cylindrical coordinates,
i.e., if the coordinates ρ
,ϕ
,andz
of a point on the curve can be expressed as
x
y
z
Δ′ ϕ
′
P
′ ′
P
′ ρ Δ ′ ϕ
Δ′ ρ
′
Δz
Figure 2.4: Elements of length, area, and volume in cylindrical coordinates. We have
used “Δ”insteadof“d.”
16
This is the only unit vector in “curvilinear coordinates” which is independent of the
position of P
.

66 Differentiation
functions of the parameter t, then we can find the differentials in terms of dt
and substitute in Equation (2.29) to find an expression analogous to Equation
(2.21). We leave this as an exercise for the reader.
The first primary surface at P
is obtained by holding ρ
constant and
letting the other two coordinates vary arbitrarily. It is clear that the resulting
surface is a cylinder of radius ρ
passing through P
. It is also clear that the
first primary length element dρ
is perpendicular to the first primary surface.
The second and third primary surfaces are, respectively, a plane containing
the z-axis and making an angle of ϕ
with the x-axis, and a plane perpen-
dicular to the z-axis and cutting it at z
. These surfaces are perpendicular to
primary surfaces
of cylindrical
coordinates
consist of a
cylinder and two
planes.
their corresponding length elements. The primary elements of area are again
obtained easily, and we merely quote the results
primary elements
of area in
cylindrical
coordinates
da
1
=(ρ
dϕ
)(dz
)=ρ
dϕ
dz
,
da
2
= dρ
dz
, (2.30)
da
3
=(dρ
)(ρ
dϕ
)=ρ
dρ
dϕ
.
Finally, the volume element is
element of volume
in cylindrical
coordinates
dV =(dρ
)(ρ
dϕ
)(dz
)=ρ
dρ
dϕ
dz
. (2.31)
Table 2.2 gathers together all the elements of primary length, surface, and
volume for the three commonly used coordinate systems.
Example 2.3.1.
Examples of elements in various coordinate systems
(a) The element of length in the ϕ direction at a point with spherical coordinates
(a, γ, ϕ)isa sin γdϕ. Note that this element is independent of ϕ, and for a fixed a,
it has the largest value when γ = π/2, corresponding to the equatorial plane.
(b) The element of area for a cone of half-angle α is r sin αdrdϕ,becauseforacone,
θ is a constant (in this case, α).
Coordinate Primary Primary Volume
system length area element
elements elements
1st: dx dy dz
Cartesian 2nd: dy dx dz dx dy dz
(x, y, z) 3rd: dz dx dy
1st: dρ ρdϕdz
Cylindrical 2nd: ρdϕ dρ dz ρdρdϕdz
(ρ, ϕ, z) 3rd: dz ρdρdϕ
1st: dr r
2
sin θdθdϕ
Spherical 2nd: rdθ r sin θdrdϕ r
2
sin θdrdθdϕ
(r, θ, ϕ) 3rd: r sin θdϕ rdrdθ
Table 2.2: Primary length and area as well as volume elements in the three common
coordinate systems. In almost all applications of the next chapter each of these variables
carries a prime.
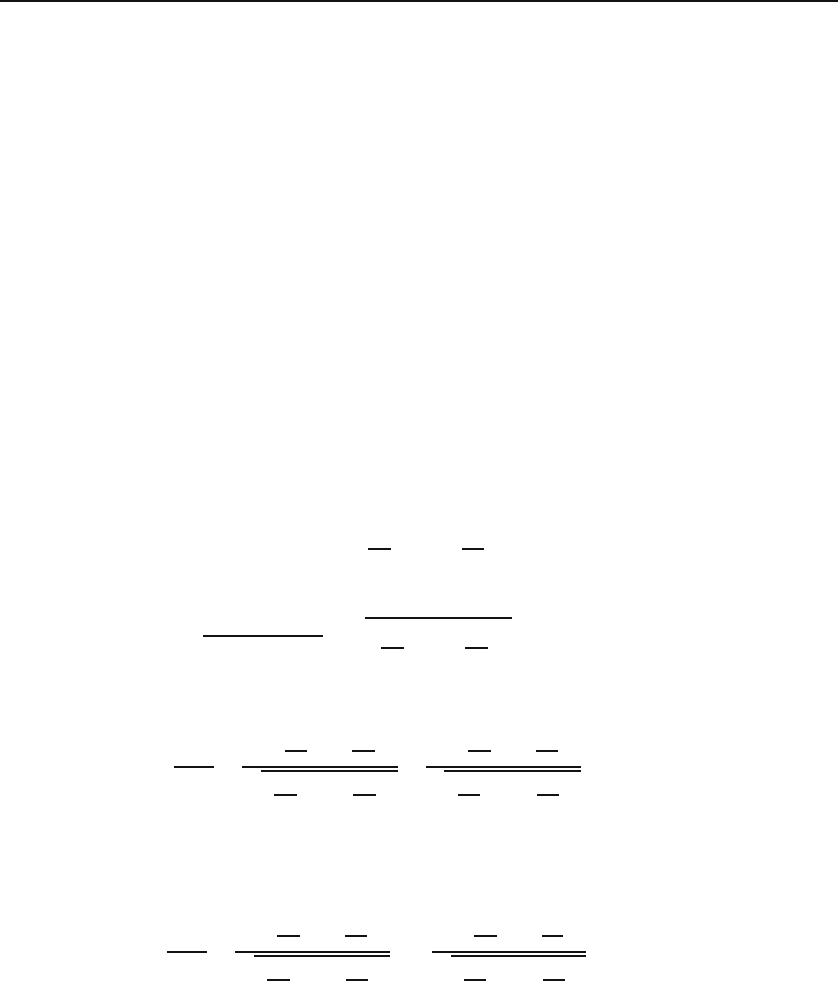
2.3 Elements of Length, Area, and Volume 67
(c) The element of area of a cylinder of radius a is adϕdz.
(d) The element of area of a sphere of radius a is a
2
sin θdθdϕ. Note that the largest
element of area (for given dθ and dϕ) is at the equator and the smallest (zero) at
the two poles.
(e) The element of area of a half-plane containing the z-axis and making an angle
α with the x-axis is dρ dz, independent of the angle α.
Example 2.3.2. Suppose Cartesian coordinates of the plane are related to two finding unit
vectors without
use of geometry!
other variables u and v via the formulas
x = f (u, v),y= g(u, v).
We want to consider u and v as coordinates and find the unit vectors corresponding
to them using our knowledge of differentiation gained in this chapter without any
resort to geometric arguments.
In general, the unit vector in the direction of any coordinate variable at a point P
is obtained by increasing the coordinate slightly (keeping other coordinate variables
constant), calculating the displacement vector described by the motion of P ,and
dividing this vector by its length. So, consider changing u while v is kept constant.
Call the displacement obtained Δ
l
1
.Then
Δ
l
1
=
ˆ
e
x
Δx +
ˆ
e
y
Δy =
ˆ
e
x
∂f
∂u
Δu +
ˆ
e
y
∂g
∂u
Δu
and
|Δ
l
1
| =
(Δx)
2
+(Δy)
2
=
"
∂f
∂u
2
+
∂g
∂u
2
Δu.
Therefore,
ˆ
e
u
= lim
Δu→0
Δ
l
1
|Δ
l
1
|
=
ˆ
e
x
∂f
∂u
+
ˆ
e
y
∂g
∂u
∂f
∂u
2
+
∂g
∂u
2
=
ˆ
e
x
∂x
∂u
+
ˆ
e
y
∂y
∂u
∂x
∂u
2
+
∂y
∂u
2
.
For
ˆ
e
v
, we keep u fixed and vary v. Calling the resulting displacement Δ
l
2
,we
easily obtain
ˆ
e
v
= lim
Δv→0
Δ
l
2
|Δ
l
2
|
=
ˆ
e
x
∂f
∂v
+
ˆ
e
y
∂g
∂v
∂f
∂v
2
+
∂g
∂v
2
==
ˆ
e
x
∂x
∂v
+
ˆ
e
y
∂y
∂v
∂x
∂v
2
+
∂y
∂v
2
.
Note that for general f and g,
ˆ
e
u
and
ˆ
e
v
are not perpendicular.
The result can easily be generalized to three variables. In fact, if
x = f (u, v, w),y= g(u, v, w),z= h(u, v, w),

68 Differentiation
then, a similar calculation as above will yield
ˆ
e
u
=
ˆ
e
x
∂f
∂u
+
ˆ
e
y
∂g
∂u
+
ˆ
e
z
∂h
∂u
∂f
∂u
2
+
∂g
∂u
2
+
∂h
∂u
2
=
ˆ
e
x
∂x
∂u
+
ˆ
e
y
∂y
∂u
+
ˆ
e
z
∂z
∂u
∂x
∂u
2
+
∂y
∂u
2
+
∂z
∂u
2
,
ˆ
e
v
=
ˆ
e
x
∂f
∂v
+
ˆ
e
y
∂g
∂v
+
ˆ
e
z
∂h
∂v
∂f
∂v
2
+
∂g
∂v
2
+
∂h
∂v
2
=
ˆ
e
x
∂x
∂v
+
ˆ
e
y
∂y
∂v
+
ˆ
e
z
∂z
∂v
∂x
∂v
2
+
∂y
∂v
2
+
∂z
∂v
2
,
ˆ
e
w
=
ˆ
e
x
∂f
∂w
+
ˆ
e
y
∂g
∂w
+
ˆ
e
z
∂h
∂w
∂f
∂w
2
+
∂g
∂w
2
+
∂h
∂w
2
=
ˆ
e
x
∂x
∂w
+
ˆ
e
y
∂y
∂w
+
ˆ
e
z
∂z
∂w
∂x
∂w
2
+
∂y
∂w
2
+
∂z
∂w
2
.
2.4 Problems
2.1. Find the partial derivatives of the following functions at the given points
with respect to the given variables. In the following r =(x, y, z)andr
=
(x
,y
,z
):
e
xyz
with respect to x at (1, 0, −1),
cos(xy/z) with respect to z at (π,1, 1),
x
2
y + y
2
z + z
2
x with respect to y at (1, −1, 2),
ln
ax + by + cz
x
2
+ y
2
+ z
2
with respect to x at (a, b, c),
r ≡
x
2
+ y
2
+ z
2
with respect to x at (x, y, z),
|r − r
| with respect to y at (x, y, z, x
,y
,z
),
1
|r − r
|
with respect to z
at (x, y, z, x
,y
,z
).
2.2. The Earth has a radius of 6400 km. The thickness of the atmosphere
is about 50 km. Starting with the volume of a sphere and using differentials,
estimate the volume of the atmosphere. Hint: Find the change in the volume
of a sphere when its radius changes by a “small” amount.
2.3. The gravitational potential (potential energy per unit mass) at a distance
r from the center of the Earth (assumed to be the origin of a Cartesian
coordinate system) is given by
Φ=−
GM
r
,r=
x
2
+ y
2
+ z
2
,
where G =6.67 × 10
−11
N·m
2
/kg
2
and M =6×10
24
kg. Using differentials,
find the energy needed to raise a 10-kg object from the point with coordinates
(4000 km, 4000 km, 3000 km) to a point with coordinates (4020 km, 4050 km,
3010 km).

2.4 Problems 69
2.4. Show that the function f (x ± ct) satisfies the one-dimensional wave
equation:
one-dimensional
wave equation
∂
2
f
∂x
2
−
1
c
2
∂
2
f
∂t
2
=0.
Hint: Let y = x ± ct and use the chain rule.
2.5. Assume that f
+kf =0andg
−kg = 0. Show that F (x, y) ≡ f(x)g(y) two-dimensional
Laplace’s equation
satisfies the two-dimensional Laplace’s equation:
∂
2
F
∂x
2
+
∂
2
F
∂y
2
=0.
2.6. Suppose that f
− αf =0,g
− βg =0,andh
− γh =0. Writean
equation relating α, β,andγ such that the function
F (x, y, z) ≡ f(x)g(y)h(z)
satisfies the three-dimensional Laplace’s equation:
three-dimensional
Laplace’s equation
∂
2
F
∂x
2
+
∂
2
F
∂y
2
+
∂
2
F
∂z
2
=0.
2.7. Suppose that f
− αf =0,g
− βg =0,h
− γh =0,andu
− ωu =0.
Write an equation relating α, β, γ,andω such that the function
F (x, y, z, t) ≡ f(x)g(y)h(z)u(t)
satisfies the heat equation:
heat equation
∂
2
F
∂x
2
+
∂
2
F
∂y
2
+
∂
2
F
∂z
2
= a
∂F
∂t
.
where a is a constant.
2.8. Suppose that f
+k
2
x
f =0,g
+k
2
y
g =0,h
+k
2
z
h =0,andu
+ω
2
u =0.
(a) Write an equation relating k
x
,k
y
,k
z
,andω such that the function
F (x, y, z, t) ≡ f(x)g(y)h(z)u(t)
satisfies the three-dimensional wave equation:
three-dimensional
wave equation
∂
2
F
∂x
2
+
∂
2
F
∂y
2
+
∂
2
F
∂z
2
−
1
c
2
∂
2
F
∂t
2
=0.
(b) If ω is considered as angular frequency,andc as the speed of the wave,
what is the magnitude of the vector k ≡k
x
,k
y
,k
z
?
2.9. Consider the function F (x, y, z) ≡ f
x
2
y + y
2
x
a
2
z
in which a is a con-
stant. Assuming that f
(2) = a, find the unit vector
ˆ
e
v
in the direction of
v =
ˆ
e
x
∂
1
F (a, a, a)+
ˆ
e
y
∂
2
F (a, a, a)+
ˆ
e
z
∂
3
F (a, a, a).

70 Differentiation
2.10. Consider the function F (x, y, z) ≡ f
x
3
y − y
3
z +2z
3
x
a
4
in which a is
a constant. Assuming that f
(17) = a, find the unit vector
ˆ
e
v
in the direction
of
v =
ˆ
e
x
∂
1
F (a, −a, 2a)+
ˆ
e
y
∂
2
F (a, −a, 2a)+
ˆ
e
z
∂
3
F (a, −a, 2a).
2.11. Given that f(x, y, z)=e
−k
√
x
2
+y
2
+z
2
/
x
2
+ y
2
+ z
2
,wherek is a
constant, find the radial component (component along
ˆ
e
r
) of the vector
V =
ˆ
e
x
∂
1
f(x, y, z)+
ˆ
e
y
∂
2
f(x, y, z)+
ˆ
e
z
∂
3
f(x, y, z).
2.12. Given that
∂
1
f(x, y, z)=∂
2
f(z,x, y)=∂
3
f(y,z, x)=
2kx
y
−
kz
2
x
2
,
where k is a constant, find the function f(x, y, z). Note the order of the
variables in each pair of parentheses.
2.13. Given that f(x, y, z)=x
2
y sin (yz/x), find
∂
2
f(1, 1,π/2),∂
1
f(2,π,1),∂
3
f(4,π,1),∂
1
f(y,z, x),∂
1
f(t, u, v).
2.14. Derive the analogue of Equation (2.11) assuming this time that Q is
held constant in all derivatives instead of W .
2.15. Which of the following functions are homogeneous?
e
xy/z
2
,xyzsin
xy
az
,
x
2
y
2
z
cos
xz
y
2
,x
2
+ y
2
− z
2
,ax+ y(z − x),
where a is a constant. For those functions that are homogeneous, find their
degree and verify that they satisfy Equation (2.18).
2.16. Suppose f and g are homogeneous functions of degrees q and p, respec-
tively. What can you say about the homogeneity of f ± g, fg,andf/g.If
they are homogeneous, find their degree, and verify that they satisfy Equation
(2.18).
2.17. If f is homogeneous of degree q, show that ∂
i
f is homogeneous of degree
q − 1. Hint: Use the definition of homogeneity and differentiate with respect
to x
i
.
2.18. A function f(x, y, z) of Cartesian coordinates can also be thought of as
a function of cylindrical coordinates ρ, ϕ, z, because the latter are functions
of the former via the relations ρ =
x
2
+ y
2
and tan ϕ = y/x.
(a) Using the chain rule for differentiation, find ∂f/∂x and ∂f/∂y in terms
of ∂f/∂ρ and ∂f/∂ϕ. Express your answers entirely in terms of cylindrical
coordinates.
