Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

2.2 Partial Derivatives 51

Thus, by diﬀerentiating f(U, V, W )withrespecttoV and U and taking their ratios,

we obtain the derivative of U with respect to V ; no need to solve for U in terms of

the other three variables!

Equation (2.10) is ususlly written in a more symmetric way. The numerator of

the fraction on the RHS can be replaced using Equation (2.9). Then, the result can

be written as an important

relation used often

thermodynamics



∂U

∂V



Q,W



∂V

∂Q



U,W



∂Q

∂U



V,W

= −1. (2.11)

A simpler version of this result, in which the fourth variable W is absent, is com-

monly used in thermodynamics.



A word of caution about notation is in order. We chose the set of vari-

ables (x

,...,x

) as arguments of the function f , and then denoted the

derivative by ∂f/∂x

. We could have chosen any other set of symbols such

as (y

,...,y

), or (t

,...,t

) as the arguments. Then we would have

had to write ∂f/∂y

,or∂f/∂t

for partial derivatives. This freedom of choice confusion

surrounding the

expression

(∂f /∂x)(y,x)

and a notation

that resolves the

confusion

can become confusing because, little eﬀort is made in the literature to distin-

guish between the “free” general arguments and the speciﬁc point at which

the derivative is to be evaluated. For example, the symbol (∂f/∂x)(y, x)can

be interpreted in two ways: It can be the derivative of a function of two vari-

ables with respect to its ﬁrst argument, subsequently evaluated at the point

with coordinates (y, x), or it could be the derivative with respect to the sec-

ond argument, in a seemingly strange world in which y is used as the ﬁrst

argument! The longstanding usage of x as the ﬁrst partner of a doublet by no

means reserves the ﬁrst slot for x at all times. Therefore, the confusion above

is indeed a legitimate one.

We started the discussion by distinguishing between the free arguments

,...,x

) and the speciﬁc point (a

,...,a

). However, making this

distinction every time we write down a partial derivative can become very

clumsy. Nevertheless, the reader should always keep in mind this distinction

and write it down explicitly whenever necessary. To minimize the confusion,

we leave out all symbols but keep only the position of the variable in the array.

Speciﬁcally,

Box 2.2.2. We write ∂

f for the derivative of f with respect to its

kth argument. This derivative is a function: We can evaluate it at

,...,a

),forwhichwewrite∂

f(a

,...,a

) ≡ ∂

f(a).

This notation avoids any reference to the “free” arguments. One can choose

any symbol for the free arguments; the ﬁnal answer is independent of this

choice:

∂

f(a

,...,a

∂f(t

,...,t

)

∂t



t=a

∂f(y

,...,y

)

∂y



y=a

∂f(♥

, ♥

,...,♥

)

∂♥



(♥

,...,♥

)

52 Diﬀerentiation

because the only thing that matters is the index k which tells us with respect

to what variable we are diﬀerentiating.

Example 2.2.2.

Consider the function f(x, y, z)=e

xy/z

.Wewriteitﬁrstas

f(x

)=e

.Then

∂

f(x

)=(x

∂

f(x

)=(x

∂

f(x

)=−(x

Now that the functional form of all partial derivatives are derived, we can evaluate

them at any point we want. For example,

∂

f(1, 2, 3) =

2/3

,∂

f(1, 1, 1) = −e,

∂

f(t, u, v)=(u/v)e

tu/v

,∂

f(z, x,y)=−(zx/y

xz/y



Higher-order derivatives are deﬁned just as in the single-variable case,

except that now mixed derivatives are also possible. Thus,

∂

(∂

f) ≡ ∂

f ≡

∂

∂x

,∂

(∂

f) ≡

∂

∂x

,∂

(∂

f) ≡

∂

∂x

are all legitimate derivatives. An important property of mixed derivatives is

order of

diﬀerentiation in a

mixed derivative is

immaterial

that—for well-behaved functions—the order of diﬀerentiation is immaterial.

Example 2.2.3.

Functions which can be written as the product of single-variable

functions are important in the solution of partial diﬀerential equations. Suppose

that F(x, y, z)=f(x)g(y)h(z). Then ∂

F (x, y, z)=f



(x)g(y)h(z) and the function

∂

(x, y, z)=



(x)g(y)h(z)

f(x)g(y)h(z)



(x)

f(x)

is seen to be independent of y and z. One can show similarly that

∂

(x, y, z)=



(y)

g(y)

∂

(x, y, z)=



(z)

h(z)

each one depending on only one variable.



Example 2.2.4. It is sometimes necessary to ﬁnd the most general function, one of

whose partial derivatives is given. This can be done by antidiﬀerentiating (indeﬁnite

integral) with respect to the variable of the partial derivative, treating the rest of the

variables constant. The usual “constant” of integration is replaced by a function of

the undiﬀerentiating variables. For example, suppose ∂

f(z, x,y)=ye

.Since

the third variable is y, and the partial derivative is with respect to the third variable,

we need to integrate with respect to y, keeping x and z constant. This gives

f(z, x,y)=

+ g(x, z) ⇒ f(x, y, z)=

+ g(y, x),

where g, the “constant” of integration, is an arbitrary function of the ﬁrst two

variables.



2.2 Partial Derivatives 53

Δ f

)

+ Δ x

Figure 2.1: The tangent line at x

approximates the curve in a small neighborhood of

. If conﬁned in this neighborhood, i.e., if Δx—which is equal to dx—is small, Δf

and df are approximately equal. However, df is deﬁned regardless of the size of Δx.

2.2.2 Diﬀerentials

We now introduce the notion of diﬀerentials. Recall from calculus that, in diﬀerentials

the case of one variable, the diﬀerential of a function is related to a linear

approximation of that function (see Figure 2.1). Basically, the tangent line at

apointx

is considered as the linear approximation to the curve representing

the function f in the neighborhood of x

. The increment in the value of the

function representing the tangent line—denoted by df (x

)—when x

changes

to x

+Δx,isgivenby

df (x

) ≡





Δx ≡





dx,

where, as a matter of notation, Δx has been replaced by dx, because by deﬁ-

nition, the diﬀerential of an independent variable is nothing but its increment.

The above equation is not an approximation: dx can be any number, large or

small, and df (x

) will be correspondingly large or small. The approximation

starts when we try to replace Δf with df : The smaller the Δx = dx,the

better the approximation Δf(x

) ≈ df (x

). The generalization of this idea

to two variables involves approximating the surface representing the function

f(x, y) by its tangent plane. For more variables, no visualizable geometric

interpretation is possible, but the basic idea is to replace the Δ’s with d’s and

the approximation with equality in Box 2.2.1. The result is

df =

∂f

∂x

∂f

∂x

+ ···+

∂f

∂x



i=1

∂f

∂x

. (2.12)

We note that dx

’s in Equation (2.12) determine the independent variables

on which f depends, and the coeﬃcient of dx

is ∂f/∂x

. This observation is

the basis of transforming functions in such a way that the resulting functions

depend on variables which are physically more useful. To be speciﬁc, suppose a

function f exists which depends on (x, y, z), but from a physical perspective,

a function which depends on the derivative of f with respect to its second

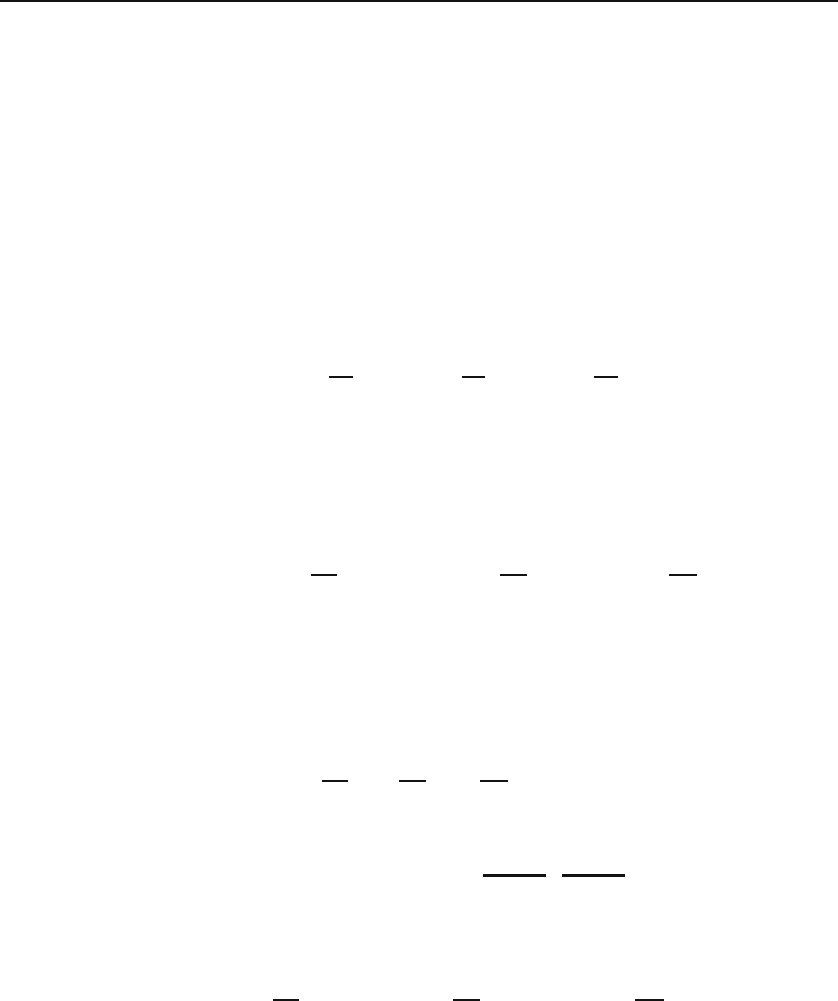
54 Diﬀerentiation

argument, and not on the second argument itself, is more valuable. This

function can be obtained by a Legendre transformation on f, obtained

Legendre

transformation

by subtracting from f the product of the second argument and the derivative

of f with respect to that argument. So, deﬁne a new function g by

g ≡ f − y∂

f ≡ f −yh where h = ∂

Then, we get

dg = df − hdy− ydh= ∂

fdx+ ∂

fdy+ ∂

fdz−hdy−ydh

= ∂

fdx+ ∂

fdz−ydh.

The diﬀerentials on the RHS of the last line indicate that the “natural” inde-

pendent variables for g are x, z,andh,andthat

∂g

∂x

= ∂

∂g

∂z

= ∂

∂g

∂h

= −y.

Legendre transformation is used frequently in thermodynamics and mechanics.

Example 2.2.5.

The internal energy U of a thermodynamical system is a function

of entropy S,volumeV , and number of moles N. These variables are called the

natural variables of U,andwewriteU(S, V, N). Temperature T , pressure P ,andnatural variables

of thermodynamic

functions

chemical potential μ, are deﬁned as follows:

T =



∂U

∂S



V,N

,P= −



∂U

∂V



S,N

,μ=



∂U

∂N



S,V

where, as is common in thermodynamics, we have indicated the variables that are

held constant as subscripts. Entropy is a hard quantity to measure: If we were to

measure ∂U/∂S, we would have to ﬁnd the ratio of the change of U to that of S;

not an easy task! On the other hand, T is easy to measure, and thus it is desirable

to Legendre transform U to obtain a function which has T as a natural variable.

The Helmholtz free energy F is deﬁned as F = U − ST.WenotethatsinceHelmholtz free

energy

dU =

∂U

∂S

dS +

∂U

∂V

dV +

∂U

∂N

dN = TdS− PdV + μdN,

we have

dF = dU − SdT − TdS = TdS − PdV + μdN



 

=dU

−SdT − TdS

= −SdT − PdV + μdN

and, therefore



∂F

∂T



V,N

= −S,



∂F

∂V



T,N

= −P,



∂F

∂N



T,V

= μ.

Helmholtz free energy is by far the most frequently used thermodynamic function,

because all its “natural” variables, namely, T , V ,andN, are easily measurable

quantities.



2.2 Partial Derivatives 55

2.2.3 Chain Rule

In many cases of physical interest, the “independent” variables x

may in

turn depend on one or more variables. Let us denote these new independent

variables by (t

,...,t

) and the functional dependence of x

by g

,sothat

= g

,...,t

) ≡ g

(t),i=1, 2,...,n. (2.13)

As the t’s vary, so will the x’s and consequently the function f . Therefore, f

becomes dependent on the t’s and we can talk about partial derivatives of f

with respect to one of the t’s. To ﬁnd such a partial derivative, we go back to

Box 2.2.1 and substitute for Δx

in terms of Δt’s. From (2.13), we have

Δx

≈

∂g

∂t

Δt

∂g

∂t

Δt

+ ···+

∂g

∂t

Δt



j=1

∂g

∂t

Δt

,i=1, 2,...,n.

Substituting this in the equation of Box 2.2.1 yields

Δf ≈

∂f

∂x



j=1

∂g

∂t

Δt

∂f

∂x



j=1

∂g

∂t

Δt

+ ···+

∂f

∂x



j=1

∂g

∂t

Δt



i=1

∂f

∂x



j=1

∂g

∂t

Δt

. (2.14)

Now suppose that we keep all of the t’s constant except for one, say t

.Then

Δt

=0forallj except j =7andthesumoverj will have only one nonzero

term, i.e., the seventh term. In such a case, Equation (2.14) becomes

Δf ≈

∂f

∂x

∂g

∂t

Δt

∂f

∂x

∂g

∂t

Δt

+ ···+

∂f

∂x

∂g

∂t

Δt



i=1

∂f

∂x

∂g

∂t

Δt

Dividing both sides by Δt

, taking limit, and replacing the approximation by

equality, we obtain

∂f

∂t

∂f

∂x

∂g

∂t

∂f

∂x

∂g

∂t

+ ···+

∂f

∂x

∂g

∂t



i=1

∂f

∂x

∂g

∂t

Instead of t

, we could have used any other one of the t’s, say t

,ort

217

. the chain rule

Theorem 2.2.6. (The Chain Rule).Letf (x) be a function of the x

and

= g

(t).Leth(t)=f(g

(t),g

(t),...,g

(t)) be a function of the t

,called

the composite of f and the g

.Ift

is any one of these t’s, then

∂

h(t)=



i=1

∂

f(g(t))∂

(t), (2.15)

where g =(g

,...,g

),andg(t) ≡ (g

(t),g

(t),...,g

(t)).

56 Diﬀerentiation

In words, the chain rule states that to evaluate the partial derivative of h

with respect to its pth argument (of which there are m)att, multiply the ith

partial of f evaluated at g(t)bythepth partial of g

evaluated at t and sum

over i.

Sometimes the chain rule is written in the following less precise form:

∂f

∂t



i=1

∂f

∂x

∂g

∂t



i=1

∂f

∂x

∂t

, (2.16)

where in the last line we have substituted x

for g

Example 2.2.7.

Suppose F is a function of three variables given by

F (x, y, z)=f





where f is some given function, and a is a constant. Let us calculate all partial

derivatives of F at (a, 2a, a) assuming that f



(2) = a. Denote the single variable of

f by u,sothatF is obtained by substituting x

y/(az

)foru in f (u). The chain

rule gives

∂

F (x, y, z)=f



(u)∂

u = f



(u)

2xy

∂

F (x, y, z)=f



(u)∂

u = f



(u)

∂

F (x, y, z)=f



(u)∂

u = −2f



(u)

If x = a, y =2a,andz = a,thenu = a

(2a)/a

=2,and

∂

F (a, 2a, a)=f



(2)

2a(2a)

=4.

Similarly, ∂

F (a, 2a, a)=1and∂

F (a, 2a, a)=−4.

In the notation of Theorem 2.2.6, there are three t’s: t

= x, t

= y, t

= z,and

only one g: g(t

)=t

/(at

). Then F becomes the composite function of f

and g.



Example 2.2.8. One of the important occasions of the use of the chain rule is in

the transformation of derivatives from Cartesian to spherical coordinates. A good

example of such a transformation occurs in quantum mechanics where an expression

such as x∂f/∂y − y∂f/∂x turns out to be related to angular momentum, and it is

most conveniently expressed in spherical coordinates. In this example we go through

the detailed exercise of converting that expression into spherical coordinates.

We start with the transformations

x = r sin θ cos ϕ, y = r sin θ sin ϕ, z = r cos θ,

and their inverse

r =



+ y

+ z

, cos θ =



+ y

+ z

, tan ϕ =

. (2.17)

2.2 Partial Derivatives 57

We shall need the derivatives of spherical coordinates with respect to x and y written how derivatives

are transformed

under a coordinate

transformation

in terms of spherical coordinates. We easily ﬁnd these by diﬀerentiating both sides

of the equations in (2.17):

∂r

∂x

∂

∂x





+ y

+ z





+ y

+ z

(2x)=

=sinθ cos ϕ,

−sin θ

∂θ

∂x

= z



−



= −

sin θ cos ϕ cos θ

⇒

∂θ

∂x

cos θ cos ϕ

sec

∂ϕ

∂x

= −

sin ϕ

r sin θ cos

⇒

∂ϕ

∂x

= −

sin ϕ

r sin θ

Similarly,

∂r

∂y

=sinθ sin ϕ,

∂θ

∂y

cos θ sin ϕ

∂ϕ

∂y

cos ϕ

r sin θ

Therefore, using the chain rule as given in Equation (2.16), we get

∂f

∂x

∂f

∂r

∂x

∂f

∂θ

∂x

∂f

∂ϕ

∂x

=sinθ cos ϕ

∂f

∂r

cos θ cos ϕ

∂f

∂θ

−

sin ϕ

r sin θ

∂f

∂ϕ

∂f

∂y

∂f

∂r

∂y

∂f

∂θ

∂y

∂f

∂ϕ

∂y

=sinθ sin ϕ

∂f

∂r

cos θ sin ϕ

∂f

∂θ

cos ϕ

r sin θ

∂f

∂ϕ

If we multiply the ﬁrst of the last two equations by y = r sin θ sin ϕ and subtract

it from the second equation multiplied by x = r sin θ cos ϕ, the terms involving

derivatives with respect to r and θ cancel while the terms with ϕ derivatives add to

give

∂f

∂y

− y

∂f

∂x

∂f

∂ϕ

Details are left as an exercise for the reader.



There is a multitude of examples in thermodynamics, for which a mastery

of the techniques of partial diﬀerentiation is essential. A property that is used

often in thermodynamics is homogeneity of functions which we derive below.

2.2.4 Homogeneous Functions

A function is called homogeneous of degree q if multiplying all of its arguments

by a parameter λ results in the multiplication of the function itself by λ

.More

precisely,

Box 2.2.3. We say that f(x

,...,x

) is homogeneous of degree q

if f (λx

,λx

,...,λx

)=λ

f(x

,...,x

58 Diﬀerentiation

Two cases merit special consideration. When q = 1, the function changes

at exactly the same rate as its arguments: Doubling all its arguments doubles

extensive and

intensive functions

the function and so on. Such a function is called extensive.Whenq =0,

the function is called intensive,anditwill not change if all its arguments

are changed by exactly the same factor.

In many cases, we want a relation between f and its partial derivatives.

We shall ﬁnd this relation by diﬀerentiating both sides of Box 2.2.3 with

respect to λ. To avoid any confusion, let us evaluate both sides at the point

,...,b

) after diﬀerentiation. Diﬀerentiation of the RHS is easy:

RHS = qλ

q−1

f(b

,...,b

For the LHS, we ﬁrst let y

= λx

for all i =1, 2,...,n—so that we have a

single variable (one symbol) in the ith place—and note that

LHS =

∂f

∂λ



i=1

∂f

∂y

∂λ



i=1

[∂

f(y

,...,y

)]x

where we have used the fact that

∂y

∂λ

= x

—by the deﬁnition of y

. Evaluating

the result at x

= b

,weobtain

LHS =



i=1

∂

f(λb

,λb

,...,λb

Equating the LHS and the RHS, we obtain the important result

qλ

q−1

f(b

,...,b



i=1

∂

f(λb

,λb

,...,λb

)

This relation holds for all values of λ, in particular we can substitute λ =1to

obtain qf(b

,...,b



i=1

∂

f(b

,...,b

). Keep in mind that the

b’s, although ﬁxed, are completely arbitrary. In particular, one can substitute

x’s for them and arrive at the functional relation

relation between a

homogeneous

function and the

sum of its partial

derivatives

qf(x

,...,x



i=1

∂

f(x

,...,x

). (2.18)

This is the relation we were looking for.

Another important result, which the reader is asked to derive in Problem

2.17, is

Box 2.2.4. If f is homogeneous of degree q,then∂

f is homogeneous of

degree q − 1.

2.3 Elements of Length, Area, and Volume 59

Example 2.2.9. We have already seen that the natural variables of the internal extensive and

intensive variables

thermodynamics

and their relation

to homogeneous

functions

energy U of a thermodynamical system are entropy S,volumeV ,andnumberof

moles N. Based on physical intuition, we expect the total internal energy, entropy,

volume and number of moles of the combined system to be doubled when two iden-

tical systems are brought together. We conclude that the internal energy function

increases by the same factor as its arguments. A thermodynamic quantity that has

this property is called an extensive variable. It follows that U is an extensive

variable and a homogeneous function of degree one.

Now consider temperature T , pressure P , and chemical potential μ,whichare

all partial derivatives of U with respect to its natural variables. From Problem

2.17, we conclude that these quantities are homogeneous of degree zero. It follows

that, if we bring two identical systems together, temperature, pressure, and the

chemical potential will not change, a result expected on physical grounds. Such a

thermodynamic quantity is called an intensive variable.



2.3 Elements of Length, Area, and Volume

We mentioned earlier the signiﬁcance of the second interpretation of the

derivative in conjunction with density. This interpretation is often used in

reverse order, i.e., in writing the inﬁnitesimal (element) of the physical quan-

tity as a product of density and the element of volume (or area, or length).

These elements appear inside integrals and will be integrated over (see the

next chapter). As a concrete example, let us consider the mass element which

canbeexpressedas

volume distribution: dm(r



)=ρ(r



) dV (r



)

surface distribution: dm(r



)=σ(r



) da(r



)

linear distribution: dm(r



)=λ(r



) dl(r



)

where r



denotes the coordinates of the location of the element of mass.

The relations above reduce the problem to that of writing the elements

of volume, area, and length. Most of the time, the evaluation of the integral

simpliﬁes considerably if we choose the correct coordinate system. Therefore,

we need these elements in all three coordinate systems.

Basic to the calculation of all elements are elements of length in the direc-

tion of unit vectors in any of the three coordinate systems. First we deﬁne

Box 2.3.1. The primary curve along any given coordinate is the curve

obtained when that coordinate is allowed to vary while the other two coor-

dinates are held ﬁxed.

The primary length elements are inﬁnitesimal lengths along the primary primary length

elements

curves. By construction, they are also inﬁnitesimal lengths along unit vectors.

To ﬁnd a primary length element at point P



with position vector r



along

60 Diﬀerentiation

a given unit vector, one keeps the other two coordinates ﬁxed and allows

the given coordinate to change by an inﬁnitesimal amount.

This procedure

displaces P



an inﬁnitesimal distance. The length of this displacement, written

in terms of the coordinates of P



, is the primary length element along the

given unit vector. Once the three primary length elements are found, we

can calculate area and volume elements by multiplying appropriate length

elements.

A notion related to the primary length is

Box 2.3.2. A primary surface perpendicular to a primary length is

obtained when the coordinate determining the primary length is held ﬁxed

and the other two coordinates are allowed to vary arbitrarily.

The primary element of area at a point on a primary surface is, by deﬁni-primary area

elements

tion, the product of the two primary length elements whose coordinates deﬁne

that surface.

Integrating over a primary surface of a coordinate system is facilitated if

all boundaries of the surface can be described by q

= c

where q

is either of

the two coordinates that vary on the surface and c

is a constant. For example,

the third primary surface in Cartesian coordinates is a plane parallel to the

xy-plane. A problem involving integration on this plane becomes simplest if

the boundaries of the region of integration are of the form, x = c

and y = c

i.e., if the region of integration is a rectangle.

Finally, by taking the product of all three primary length elements, we

obtain the volume element in the given coordinate system.

2.3.1 Elements in a Cartesian Coordinate System

Consider the point P



with coordinates (x



) as shown in Figure 2.2. To

ﬁnd the primary length along



keep y



and z



ﬁxed and let x



change to x



+ dx



.ThenP



will be displaced by dx



along

.Thus,the

ﬁrst primary length element—denoted by dl

—is simply dx



. Similarly, we

have dl

= dy



,anddl

= dz



. A general inﬁnitesimal displacement, which is

a vector, can be written as

general Cartesian

inﬁnitesimal

displacement



l =



≡ dr



. (2.19)

Figure 2.2 shows that d



l represents the displacement vector from P



,with

position vector r



,toaneighboring point P



, with position vector r



.But

this displacement is simply the increment in the position vector of P



.Thatis

why dr



is also used for d



l. Note that this vectorial inﬁnitesimal displacement

Usually an inﬁnitesimal amount is expressed by a diﬀerential. Thus, an increment in x

is simply dx.

Recall that this equality holds in Cartesian—and only in Cartesian—coordinates, where

the unit vectors are independent of the coordinates of P

