Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.

1.4 Relations Among Unit Vectors 31
Example 1.3.7. Achargeq moves with constant speed v (assumed to be small
compared to the speed of light) on a straight line. We want to calculate the magnetic
field produced by the charge at a point P located at a distance ρ from the line as a
function of time. Cylindrical coordinates are most suitable for this problem because
of the existence of a natural axis. Choose the path of the charge to be the z-axis.
Also assume that P lies in the xy-plane, and that q was at the origin at t =0. Then
v = v
ˆ
e
z
, r = ρ
ˆ
e
ρ
, r
1
= vt
ˆ
e
z
, r − r
1
= ρ
ˆ
e
ρ
− vt
ˆ
e
z
.So
|r − r
1
| =
(ρ
ˆ
e
ρ
− vt
ˆ
e
z
) · (ρ
ˆ
e
ρ
− vt
ˆ
e
z
)=
ρ
2
+ v
2
t
2
and v × (r − r
1
)=v
ˆ
e
z
× (ρ
ˆ
e
ρ
− vt
ˆ
e
z
)=ρv
ˆ
e
ϕ
. Therefore, the magnetic field is
B =
k
m
qv × (r − r
1
)
|r − r
1
|
3
=
k
m
qρv
(ρ
2
+ v
2
t
2
)
3/2
ˆ
e
ϕ
.
Readers familiar with the relation between magnetic fields and currents in long wires
will note that the magnetic field above obeys the right-hand rule.
1.4 Relations Among Unit Vectors
We have seen that, depending on the nature of problems encountered in
physics, one coordinate system may be more useful than others. We have
also seen that the coordinates can be transformed back and forth using func-
tional relations that connect them. Since many physical quantities are vectors,
transformation and expression of components in bases of various coordinate
systems also become important. The key to this transformation is writing one
set of unit vectors in terms of others. In the derivation of these relations, we
shall make heavy use of Box 1.1.2.
First we write the cylindrical unit vectors in terms of Cartesian unit vec-
tors. Since {
ˆ
e
x
,
ˆ
e
y
,
ˆ
e
z
} form a basis, any vector can be written in terms of
them. In particular,
ˆ
e
ρ
can be expressed as
ˆ
e
ρ
= a
1
ˆ
e
x
+ b
1
ˆ
e
y
+ c
1
ˆ
e
z
(1.35)
with a
1
, b
1
,andc
1
to be determined. Next we recall that
Box 1.4.1. The dot product of two unit vectors is the cosine of the angle
between them.
Furthermore, Figure 1.12 shows that the angle between
ˆ
e
ρ
and
ˆ
e
x
is ϕ,and
that between
ˆ
e
ρ
and
ˆ
e
y
is π/2 − ϕ. So, by dotting both sides of Equation
(1.35) by
ˆ
e
x
,
ˆ
e
y
,and
ˆ
e
z
in succession, we obtain
ˆ
e
x
·
ˆ
e
ρ
=cos ϕ
= a
1
+0+0=a
1
⇒ a
1
=cosϕ,
ˆ
e
y
·
ˆ
e
ρ
=sin ϕ
=0+b
1
+0=b
1
⇒ b
1
=sinϕ,
ˆ
e
z
·
ˆ
e
ρ
=0
=0+0+c
1
= c
1
⇒ c
1
=0.

32 Coordinate Systems and Vectors
Therefore,
ˆ
e
ρ
=
ˆ
e
x
cos ϕ +
ˆ
e
y
sin ϕ.
With the first and third cylindrical unit vectors
ˆ
e
ρ
and
ˆ
e
z
at our disposal,
16
we can determine the second, using Equation (1.5):
ˆ
e
ϕ
=
ˆ
e
z
×
ˆ
e
ρ
=det
⎛
⎝
ˆ
e
x
ˆ
e
y
ˆ
e
z
001
cos ϕ sin ϕ 0
⎞
⎠
= −
ˆ
e
x
sin ϕ +
ˆ
e
y
cos ϕ.
Thus,
ˆ
e
ρ
=
ˆ
e
x
cos ϕ +
ˆ
e
y
sin ϕ,
ˆ
e
ϕ
= −
ˆ
e
x
sin ϕ +
ˆ
e
y
cos ϕ, (1.36)
ˆ
e
z
=
ˆ
e
z
.
cylindrical unit
vectors in terms of
Cartesian unit
vectors
This equation can easily be inverted to find the Cartesian unit vectors in
terms of the cylindrical unit vectors. For example, the coefficients in
ˆ
e
x
= a
2
ˆ
e
ρ
+ b
2
ˆ
e
ϕ
+ c
2
ˆ
e
z
can be obtained by dotting both sides of it with
ˆ
e
ρ
,
ˆ
e
ϕ
,and
ˆ
e
z
, respectively,
ˆ
e
ρ
·
ˆ
e
x
= a
2
+0+0 ⇒ cos ϕ = a
2
,
ˆ
e
ϕ
·
ˆ
e
x
=0+b
2
+0 ⇒−sin ϕ = b
2
,
ˆ
e
z
·
ˆ
e
x
=0+0+c
2
⇒ 0=c
2
,
wherewehaveused
ˆ
e
ρ
·
ˆ
e
x
=cosϕ,and
ˆ
e
ϕ
·
ˆ
e
x
= −sin ϕ—obtained by
dotting the first and second equations of (1.36) with
ˆ
e
x
—as well as
ˆ
e
z
·
ˆ
e
x
=0.
Similarly, one can obtain
ˆ
e
y
in terms of the cylindrical unit vectors. The entire
result is
ˆ
e
x
=
ˆ
e
ρ
cos ϕ −
ˆ
e
ϕ
sin ϕ
ˆ
e
y
=
ˆ
e
ρ
sin ϕ +
ˆ
e
ϕ
cos ϕ (1.37)
ˆ
e
z
=
ˆ
e
z
Cartesian unit
vectors in terms of
cylindrical unit
vectors
Now we express the spherical unit vectors in terms of the cylindrical ones.
This is easily done for
ˆ
e
r
, because it has only
ˆ
e
ρ
and
ˆ
e
z
components (why?).
Thus, with
ˆ
e
r
= a
3
ˆ
e
ρ
+ b
3
ˆ
e
z
,
we obtain
ˆ
e
ρ
·
ˆ
e
r
= a
3
+0 ⇒ a
3
=sinθ,
ˆ
e
z
·
ˆ
e
r
=0+b
3
⇒ b
3
=cosθ,
16
Remember that
ˆ
e
z
is a unit vector in both coordinate systems. So, one can say that
the cylindrical
ˆ
e
z
has components 0, 0, 1 in the Cartesian basis {
ˆ
e
x
,
ˆ
e
y
,
ˆ
e
z
}.

1.4 Relations Among Unit Vectors 33
where in the last step of each line, we used the fact that the angle between
ˆ
e
r
and
ˆ
e
z
is θ and that between
ˆ
e
r
and
ˆ
e
ρ
is π/2 − θ (see Figure 1.13). With a
3
and b
3
so determined, we can write
ˆ
e
r
=
ˆ
e
ρ
sin θ +
ˆ
e
z
cos θ.
Having two spherical unit vectors
ˆ
e
r
and
ˆ
e
ϕ
at our disposal,
17
we can
determine the third one, using (1.5) and (1.30):
ˆ
e
θ
=
ˆ
e
ϕ
×
ˆ
e
r
=det
⎛
⎝
ˆ
e
ρ
ˆ
e
ϕ
ˆ
e
z
010
sin θ 0cosθ
⎞
⎠
=
ˆ
e
ρ
cos θ −
ˆ
e
z
sin θ.
Thus,
ˆ
e
r
=
ˆ
e
ρ
sin θ +
ˆ
e
z
cos θ,
ˆ
e
θ
=
ˆ
e
ρ
cos θ −
ˆ
e
z
sin θ, (1.38)
ˆ
e
ϕ
=
ˆ
e
ϕ
.
spherical unit
vectors in terms of
cylindrical unit
vectors
The inverse relations can be obtained as before. We leave the details of
the calculation as an exercise for the reader.
Combining Equations (1.36) and (1.38), we can express spherical unit vec-
tors in terms of the Cartesian unit vectors:
spherical unit
vectors in terms of
Cartesian unit
vectors
ˆ
e
r
=
ˆ
e
x
sin θ cos ϕ +
ˆ
e
y
sin θ sin ϕ +
ˆ
e
z
cos θ,
ˆ
e
θ
=
ˆ
e
x
cos θ cos ϕ +
ˆ
e
y
cos θ sin ϕ −
ˆ
e
z
sin θ, (1.39)
ˆ
e
ϕ
= −
ˆ
e
x
sin ϕ +
ˆ
e
y
cos ϕ.
Equations (1.39) and (1.36) are very useful when calculating vector quan-
tities in spherical and cylindrical coordinates as we shall see in many examples
to follow. These equations also allow us to express a unit vector in one of the
three coordinate systems in terms of the unit vectors of any other coordinate
system.
Example 1.4.1.
P
1
and P
2
have Cartesian coordinates (1, 1, 1) and (−1, 2, −1),
respectively. A vector a has spherical components 0, 2, 0 at P
1
. We want to find
the spherical components of a at P
2
.Thesearegivenbya ·
ˆ
e
r
2
, a ·
ˆ
e
θ
2
,anda ·
ˆ
e
ϕ
2
.
In order to calculate these dot products, it is most convenient to express all vectors
in Cartesian form. So, using Equation (1.39), we have
a =2
ˆ
e
θ
1
=2(
ˆ
e
x
cos θ
1
cos ϕ
1
+
ˆ
e
y
cos θ
1
sin ϕ
1
−
ˆ
e
z
sin θ
1
) ,
where (r
1
,θ
1
,ϕ
1
) are coordinates of P
1
. We can calculate these from the Cartesian
coordinates of P
1
:
r
1
=
1
2
+1
2
+1
2
=
√
3, cos θ
1
=
z
1
r
1
=
1
√
3
, tan ϕ
1
=
y
1
x
1
=1 ⇒ ϕ
1
=
π
4
.
17
Recall that
ˆ
e
ϕ
is both a cylindrical and a spherical unit vector.

34 Coordinate Systems and Vectors
Therefore,
a =2
ˆ
e
x
1
√
3
1
√
2
+
ˆ
e
y
1
√
3
1
√
2
−
ˆ
e
z
2
3
=
2
√
6
ˆ
e
x
+
2
√
6
ˆ
e
y
−
4
√
6
ˆ
e
z
.
Now we need to express
ˆ
e
r
2
,
ˆ
e
θ
2
,and
ˆ
e
ϕ
2
in terms of Cartesian unit vectors.
Once again we use Equation (1.39) for which we need the spherical coordinates of
P
2
:
r
2
=
(−1)
2
+2
2
+(−1)
2
=
√
6, cos θ
2
=
z
2
r
2
= −
1
√
6
, tan ϕ
2
=
y
2
x
2
= −2.
Similarly, Equations (1.11) and (1.12) yield
sin θ
2
=+
5
6
, cos ϕ
2
= −
1
√
5
, sin ϕ
2
=+
2
√
5
.
Then
ˆ
e
r
2
=
ˆ
e
x
sin θ
2
cos ϕ
2
+
ˆ
e
y
sin θ
2
sin ϕ
2
+
ˆ
e
z
cos θ
2
=
ˆ
e
x
5
6
−
1
√
5
+
ˆ
e
y
5
6
2
√
5
−
ˆ
e
z
1
√
6
= −
1
√
6
ˆ
e
x
+
2
√
6
ˆ
e
y
−
1
√
6
ˆ
e
z
,
ˆ
e
θ
2
=
ˆ
e
x
cos θ
2
cos ϕ
2
+
ˆ
e
y
cos θ
2
sin ϕ
2
−
ˆ
e
z
sin θ
2
=
ˆ
e
x
−
1
√
6
−
1
√
5
+
ˆ
e
y
−
1
√
6
2
√
5
−
ˆ
e
z
5
6
=
1
√
30
ˆ
e
x
−
2
√
30
ˆ
e
y
−
5
√
30
ˆ
e
z
,
ˆ
e
ϕ
2
= −
ˆ
e
x
sin ϕ
2
+
ˆ
e
y
cos ϕ
2
= −
2
√
5
ˆ
e
x
−
1
√
5
ˆ
e
y
.
We can now take the dot products required for the components:
r comp = a ·
ˆ
e
r
2
=
2
√
6
ˆ
e
x
+
2
√
6
ˆ
e
y
−
4
√
6
ˆ
e
z
·
−
1
√
6
ˆ
e
x
+
2
√
6
ˆ
e
y
−
1
√
6
ˆ
e
z
= −
2
6
+
4
6
+
4
6
=1,
θ comp = a ·
ˆ
e
θ
2
=
2
√
6
ˆ
e
x
+
2
√
6
ˆ
e
y
−
4
√
6
ˆ
e
z
·
1
√
30
ˆ
e
x
−
2
√
30
ˆ
e
y
−
5
√
30
ˆ
e
z
=
2
6
√
5
−
4
6
√
5
+
20
6
√
5
=
3
√
5
,
ϕ comp = a ·
ˆ
e
ϕ
2
=
2
√
6
ˆ
e
x
+
2
√
6
ˆ
e
y
−
4
√
6
ˆ
e
z
·
−
2
√
5
ˆ
e
x
−
1
√
5
ˆ
e
y
= −
4
√
30
−
2
√
30
= −
6
√
30
= −
6
5
.
It now follows that
a =
ˆ
e
r
2
+
3
√
5
ˆ
e
θ
2
−
6
5
ˆ
e
ϕ
2
.

1.4 Relations Among Unit Vectors 35
Asacheck,wenotethat
|a| =
1
2
+
3
√
5
2
+
−
6
5
2
=
5+9+6
5
=
√
4=2,
which agrees with the length of a.
Example 1.4.2. Points P
1
and P
2
have spherical coordinates (r
1
,θ
1
,ϕ
1
)and
(r
2
,θ
2
,ϕ
2
), respectively. We want to find: (a) the angle between their position
vectors r
1
and r
2
in terms of their coordinates; (b) the spherical components of r
2
at P
1
; and (c) the spherical components of r
1
at P
2
. Once again, we shall express
all vectors in terms of Cartesian unit vectors when evaluating dot products.
(a) The cosine of the angle—call it γ
12
—between the position vectors is simply
ˆ
e
r
1
·
ˆ
e
r
2
. We can readily find this by using Equation (1.39):
cos γ
12
=
ˆ
e
r
1
·
ˆ
e
r
2
=(
ˆ
e
x
sin θ
1
cos ϕ
1
+
ˆ
e
y
sin θ
1
sin ϕ
1
+
ˆ
e
z
cos θ
1
)
· (
ˆ
e
x
sin θ
2
cos ϕ
2
+
ˆ
e
y
sin θ
2
sin ϕ
2
+
ˆ
e
z
cos θ
2
)
=sinθ
1
cos ϕ
1
sin θ
2
cos ϕ
2
+sinθ
1
sin ϕ
1
sin θ
2
sin ϕ
2
+cosθ
1
cos θ
2
=sinθ
1
sin θ
2
(cos ϕ
1
cos ϕ
2
+sinϕ
1
sin ϕ
2
)+cosθ
1
cos θ
2
=sinθ
1
sin θ
2
cos(ϕ
1
− ϕ
2
)+cosθ
1
cos θ
2
.
(b) To find the spherical components of r
2
at P
1
, we need to take the dot product
of r
2
with the spherical unit vectors at P
1
:
r comp = r
2
·
ˆ
e
r
1
= r
2
ˆ
e
r
2
·
ˆ
e
r
1
= r
2
[sin θ
1
sin θ
2
cos(ϕ
1
− ϕ
2
)+cosθ
1
cos θ
2
] ,
θ comp = r
2
·
ˆ
e
θ
1
= r
2
ˆ
e
r
2
·
ˆ
e
θ
1
= r
2
(
ˆ
e
x
sin θ
2
cos ϕ
2
+
ˆ
e
y
sin θ
2
sin ϕ
2
+
ˆ
e
z
cos θ
2
)
· (
ˆ
e
x
cos θ
1
cos ϕ
1
+
ˆ
e
y
cos θ
1
sin ϕ
1
−
ˆ
e
z
sin θ
1
)
= r
2
(sin θ
2
cos ϕ
2
cos θ
1
cos ϕ
1
+sinθ
2
sin ϕ
2
cos θ
1
sin ϕ
1
− cos θ
2
sin θ
1
)
= r
2
[sin θ
2
cos θ
1
cos(ϕ
1
− ϕ
2
) − cos θ
2
sin θ
1
],
ϕ comp = r
2
·
ˆ
e
ϕ
1
= r
2
ˆ
e
r
2
·
ˆ
e
ϕ
1
= r
2
(
ˆ
e
x
sin θ
2
cos ϕ
2
+
ˆ
e
y
sin θ
2
sin ϕ
2
+
ˆ
e
z
cos θ
2
) · (−
ˆ
e
x
sin ϕ
1
+
ˆ
e
y
cos ϕ
1
)
= r
2
(−sin θ
2
cos ϕ
2
sin ϕ
1
+sinθ
2
sin ϕ
2
cos ϕ
1
)=r
2
sin θ
2
sin(ϕ
2
− ϕ
1
).
(c) The spherical components of r
1
at P
2
can be found similarly. In fact,
switching the indices “1” and “2” in the expressions of part (b) gives the desired
formulas.
Example 1.4.3. To illustrate further the conversion of vectors from one coordinate
system to another, consider a charge q that is located at the cylindrical coordinates
(a, π/3, −a). We want to find the spherical components of the electrostatic field E
of this charge at a point P with Cartesian coordinates (a, a, a).
The most straightforward way of doing this is to convert all coordinates to
Cartesian, find the field, and then take the dot products with appropriate unit
vectors. The Cartesian coordinates of the charge are
x
q
= ρ
q
cos ϕ
q
= a cos
π
3
=
1
2
a,
y
q
= ρ
q
sin ϕ
q
= a sin
π
3
=
√
3a
2
=0.866a,
z
q
= −a.
36 Coordinate Systems and Vectors
Thus,
r − r
q
=(a −
1
2
a)
ˆ
e
x
+(a − 0.866a)
ˆ
e
y
+(a −(−a))
ˆ
e
z
=0.5a
ˆ
e
x
+0.134a
ˆ
e
y
+2a
ˆ
e
z
and
|r − r
q
| =
(0.5a)
2
+(0.134a)
2
+(2a)
2
=2.066a,
and the electric field at P can be written in terms of Cartesian unit vectors at P :
E =
k
e
q
|r − r
q
|
3
(r − r
q
)=k
e
q
0.5a
ˆ
e
x
+0.134a
ˆ
e
y
+2a
ˆ
e
z
(2.066a)
3
= k
e
q
0.5
ˆ
e
x
+0.134
ˆ
e
y
+2
ˆ
e
z
8.818a
2
=
k
e
q
a
2
(0.0567
ˆ
e
x
+0.0152
ˆ
e
y
+0.2268
ˆ
e
z
).
To find the spherical components of the field at P , we first express the spherical
unit vectors at P in terms of Cartesian unit vectors. For this, we need the spherical
coordinates of P :
r =
a
2
+ a
2
+ a
2
=
√
3 a =1.732a,
cos θ =
z
r
=
a
√
3 a
=
1
√
3
=0.577 ⇒ θ =0.955,
tan ϕ =
y
x
=
a
a
=1 ⇒ ϕ =
π
4
=0.785.
It now follows that
ˆ
e
r
=
ˆ
e
x
sin θ cos ϕ +
ˆ
e
y
sin θ sin ϕ +
ˆ
e
z
cos θ =0.577
ˆ
e
x
+0.577
ˆ
e
y
+0.577
ˆ
e
z
,
ˆ
e
θ
=
ˆ
e
x
cos θ cos ϕ +
ˆ
e
y
cos θ sin ϕ −
ˆ
e
z
sin θ =0.408
ˆ
e
x
+0.408
ˆ
e
y
− 0.816
ˆ
e
z
,
ˆ
e
ϕ
= −
ˆ
e
x
sin ϕ +
ˆ
e
y
cos ϕ = −0.707
ˆ
e
x
+0.707
ˆ
e
y
.
Now we take the dot product of E with these unit vectors to find its spherical
components at P . The reader may first easily check that
ˆ
e
r
·
ˆ
e
x
=0.577,
ˆ
e
r
·
ˆ
e
y
=0.577,
ˆ
e
r
·
ˆ
e
z
=0.577,
ˆ
e
θ
·
ˆ
e
x
=0.408,
ˆ
e
θ
·
ˆ
e
y
=0.408,
ˆ
e
θ
·
ˆ
e
z
= −0.816,
ˆ
e
ϕ
·
ˆ
e
x
= −0.707,
ˆ
e
ϕ
·
ˆ
e
y
=0.707,
ˆ
e
ϕ
·
ˆ
e
z
=0.
We can now finally calculate the field components:
E
r
= E ·
ˆ
e
r
=
k
e
q
a
2
(0.0567
ˆ
e
r
·
ˆ
e
x
+0.0152
ˆ
e
r
·
ˆ
e
y
+0.2268
ˆ
e
r
·
ˆ
e
z
)
=
k
e
q
a
2
(0.0567 × 0.577 + 0.0152 × 0.577 + 0.2268 ×0.577) = 0.1724
k
e
q
a
2
,
E
θ
= E ·
ˆ
e
θ
=
k
e
q
a
2
(0.0567
ˆ
e
θ
·
ˆ
e
x
+0.0152
ˆ
e
θ
·
ˆ
e
y
+0.2268
ˆ
e
θ
·
ˆ
e
z
)
=
k
e
q
a
2
(0.0567 × 0.408 + 0.0152 × 0.408 −0.2268 × 0.816) = −0.1558
k
e
q
a
2
,
E
ϕ
= E ·
ˆ
e
ϕ
=
k
e
q
a
2
(0.0567
ˆ
e
ϕ
·
ˆ
e
x
+0.0152
ˆ
e
ϕ
·
ˆ
e
y
+0.2268
ˆ
e
ϕ
·
ˆ
e
z
)
=
k
e
q
a
2
(−0.0567 ×0.707 + 0.0152 × 0.707) = −0.0294
k
e
q
a
2
.
The choice of Cartesian coordinates was the most straightforward one, but one
can choose any other coordinate system to calculate the field and find the com-
ponents in any other set of unit vectors. The reader is urged to try the other
choices.

1.5 Problems 37
1.5 Problems
1.1. Find the equation of a line that passes through the following pairs of
points:
(a) (1, 0, 1) and (−1, 1, 0). (b) (2, 2, −1) and (−2, −1, 1).
(c) (1, 1, 1) and (−1, 1, −1). (d) (1, 1, 1) and (−2, 2, 0).
(e) (0, 2, −1) and (3, −1, 1). (f) (0, 1, 0) and (−1, 0, −1).
1.2. Use Figure 1.4 and the interpretation of the a · b as the product of the
length of a with the projection of b along a to show that
(a + b) · c = a
· c + b · c.
1.3. Take the dot product of a = b−c with itself and prove the law of cosines
by interpreting the result geometrically. Note that the three vectors form a
triangle.
1.4. Find the angle between a =2
ˆ
e
x
+3
ˆ
e
y
+
ˆ
e
z
and b =
ˆ
e
x
− 6
ˆ
e
y
+2
ˆ
e
z
.
1.5. Find the angle between a =9
ˆ
e
x
+
ˆ
e
y
− 6
ˆ
e
z
and b =4
ˆ
e
x
− 6
ˆ
e
y
+5
ˆ
e
z
.
1.6. Show that a =
ˆ
e
x
cos α +
ˆ
e
y
sin α and b =
ˆ
e
x
cos β +
ˆ
e
y
sin β are unit
vectors in the xy-plane making angles α and β with the x-axis. Then take their
dot product and obtain a formula for cos(α−β). Now use sin x =cos(π/2−x)
to find the formula for sin(α − β).
1.7. Vectors a and b are the sides of a parallelogram, c and d are its diagonals,
and θ is the angle between a and b. Show that
|c|
2
+ |d|
2
=2(|a|
2
+ |b|
2
)
and that
|c|
2
−|d|
2
=4|a||b|cos θ.
1.8. Given a, b,andc—vectors from the origin to the points A, B,andC—
show that the vector (a ×b)+(b ×c)+(c ×a) is perpendicular to the plane
ABC.
1.9. Show that the vectors a =2
ˆ
e
x
−
ˆ
e
y
+
ˆ
e
z
, b =
ˆ
e
x
− 3
ˆ
e
y
− 5
ˆ
e
z
,and
c =3
ˆ
e
x
− 4
ˆ
e
y
− 4
ˆ
e
z
form the sides of a right triangle.
1.10. (a) Find the vector form of the equation of the plane defined by the three
points P , Q,andR with coordinates (p
1
,p
2
,p
3
), (q
1
,q
2
,q
3
), and (r
1
,r
2
,r
3
),
respectively. Hint: The position vector of a point X =(x, y, z) in the plane
is perpendicular to the cross product of
−−→
PQ and
−→
PR.
(b) Determine an equation for the plane passing through the points (2, −1, 1),
(3, 2, −1), and (−1, 3, 2).
1.11. Derive the law of sines for a triangle using vectors.

38 Coordinate Systems and Vectors
1.12. Using vectors, show that the diagonals of a rhombus are orthogonal.
1.13. Show that a necessary and sufficient condition for three vectors to be
in the same plane is that the dot product of one with the cross product of the
other two be zero.
1.14. Show that two nonzero vectors have the same direction if and only if
their cross product vanishes.
1.15. Show the following vector identities by writing each vector in terms of
Cartesian unit vectors and showing that each component of the LHS is equal
to the corresponding component of the RHS.
(a) a ·(b ×c)=c ·(a × b)=b · (c × a).
(b) a ×(b ×c)=b(a ·c) −c(a ·b), this is called the bac cab rule.
(c) (a ×b) ·(c × d)=(a · c)(b ·d) − (a · d)(b ·c).
(d) (a ×b) ×(c ×d)=
b[a · (c ×d)] −a[b ·(c × d)].
(e) (a ×b) ×(c × d)=c[a · (b ×d)] − d[a · (b ×c)].
(f) (a ×b) ·(a ×b)=|a|
2
|b|
2
− (a ·b)
2
.
1.16. Convert the following triplets from the given coordinate system to the
other two. All angles are in radians.
Cartesian: (1, 2, 1), (0, 0, 1), (1, −1, 0), (0, 1, 0), (1, 1, 1), (2, 2, 2), (0, 0, 5),
(1, 1, 0), (1, 0, 0).
Spherical: (2,π/3,π/4), (5, 0,π/3), (3,π/3, 3π/4), (1, 1, 0), (1, 0, 0),
(5, 0, ♣), (3,π,♥), (0, ♠, ♦).
Cylindrical: (0, ♣, 4), (2,π,0), (0, 217, −18), (1, 3π/
4, −2), (1, 2, 3), (1, 0, 0).
1.17. Derive the second and third relations in Equation (1.21).
1.18. Points P and P
have spherical coordinates (r, θ, ϕ)and(r
,θ
,ϕ
),
cylindrical coordinates (ρ, ϕ, z)and(ρ
,ϕ
,z
), and Cartesian coordinates
(x, y, z)and(x
,y
,z
), respectively. Write |r − r
| in all three coordinate
systems. Hint: Use Equation (1.2) with a = r − r
and r and r
written in
terms of appropriate unit vectors.
1.19. Show that Equation (1.24) is independent of where we choose the origin
to be. Hint: Pick a different origin O
whose position vector relative to O is
R and write the equation in terms of position vectors relative to O
and show
that the final result is the same as in Equation (1.24).
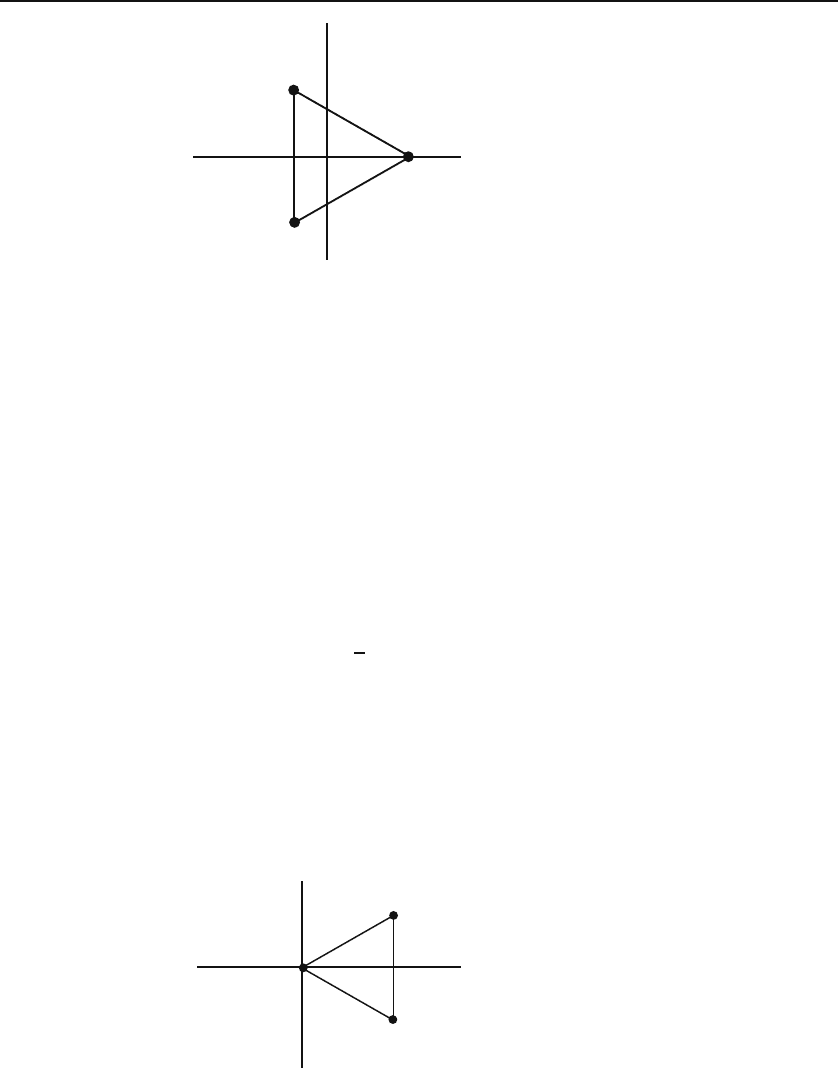
1.20. Three point charges are located at the corners of an equilateral triangle
of sides a with the origin at the center of the triangle as shown in Figure 1.19.
(a) Find the general expression for the electric field and electric potential at
(0, 0,z).
(b) Find a relation between q and Q such that the z-component of the field
vanishes for all values of z.WhatareE andΦforsuchcharges?
(c) Calculate E and Φ for z = a.
1.5 Problems 39
x
y
q
q
Q
Figure 1.19:
1.21. A point charge Q and two point charges q are located in the xy-plane
at the corners of an equilateral triangle of side a as shown in Figure 1.20.
(a) Find the potential and the Cartesian components of the electrostatic field
at (0, 0,z).
(b) Show that it is impossible for E to be along the z-axis.
(c) Calculate E for z = a and find Q in terms of q such that E
z
vanishes for
this value of z.
(d)WhatisthevalueofΦatz = a for the charges found in (c)?
1.22. Three point charges each of magnitude Q and one point charge q are
located at the corners of a square of side 2a. Using an appropriate coordinate
system.
(a) Find the electric field and potential at point P located on the diagonal
from Q to q (and beyond) a distance 2
√
2 a from the center.
(b) Find a relation, if it exists, between q and Q such that the field vanishes
at P.
1.23. Achargeq is located at the spherical coordinates (a, π/4,π/3). Find
the electrostatic potential and the Cartesian components of the electrostatic
field of this charge at a point P with spherical coordinates (a, π/6,π/4). Write
the field components as numerical multiples of k
e
q/a
2
, and the potential as a
x
y
q
q
Q
Figure 1.20:

40 Coordinate Systems and Vectors
numerical multiple of k
e
q/a.
1.24. Achargeq is located at the cylindrical coordinates (a, π/4, 2a). Find
the Cartesian components of the electrostatic field of this charge at a point P
with cylindrical coordinates (2a, π/6,a). Write your answers as a numerical
multiple of k
e
q/a
2
. Find the electrostatic potential at P and express it as a
numerical multiple of k
e
q/a.
1.25. Achargeq is located at the cylindrical coordinates (a, π/3, −a).
(a) Find the Cartesian components of the electrostatic field E of this charge
at a point P with cylindrical coordinates (a, π/4, 2a). Write your answers as
a numerical multiple of k
e
q/a
2
.
(b) Write E in terms of the cylindrical unit vectors at P .
(c) Find the electrostatic potential at P as a numerical multiple of k
e
q/a.
1.26. Two charges q and −2q are located at the cylindrical coordinates
(a, π/4,a)and(a, 2π/3, −a), respectively.
(a) Find the Cartesian components of the electrostatic field at a point P with
spherical coordinates (3a, π/6,π/4). Write your answers as a numerical mul-
tiple of k
e
q/a
2
.
(b) Find the electrostatic potential at P . Write your answer as a numerical
multiple of k
e
q/a.
1.27. Two charges 3q and −q are located at the spherical coordinates
(a, π/3,π/6) and (2a, π/6,π/4), respectively.
(a) Find the cylindrical components of the electrostatic field at a point P
with spherical coordinates (3a, π/4,π/4). Write your answers as a numerical
multiple of k
e
q/a
2
.
(b) Find the electrostatic potential at P . Write your answer as a numerical
multiple of k
e
q/a.
1.28. Achargeq is located at the spherical coordinates (a, π/3,π/6). Find
the Cartesian components of the electrostatic field of this charge at a point P
with cylindrical coordinates (a, 2π/3, 2a). Write your answers as a numerical
multiple of k
e
q/a
2
. Also find the electrostatic potential at P .
1.29. Four charges are located at Cartesian coordinates as follows: q at
(2a, 0, 0), −2q at (0, 2a, 0),
4
√
2
5
√
5
q at (−a, 0, 0), and −
2
√
2
5
√
5
q at (0, −a, 0). Find
the Cartesian components of the electrostatic field at (0, 0,a).
1.30. Charge q is moving at constant speed v along the positive x-axis. Two
other charges −q and 2q are moving at constant speeds v and 2v along positive
y and negative z axes, respectively. Assume that at t =0,q is at the origin,
−q is at (0,a,0), and 2q at (0, 0, −a).
(a) Find the Cartesian components of the magnetic field at a point (x, y, z)
for t>0.
(a) Find the cylindrical components of the magnetic field at a point (ρ, ϕ, z)
for t>0.
