Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.


CONTENTS xxiii
31.3UniversalityofChaos........................773
31.3.1 Feigenbaum Numbers . . . . . . . . . . . . . . . . . . . 773
31.3.2 Fractal Dimension . . . . . . . . . . . . . . . . . . . . . 775
31.4Problems ..............................778
32 Probability Theory 781
32.1BasicConcepts ...........................781
32.1.1 ASetTheoryPrimer....................782
32.1.2 Sample Space and Probability . . . . . . . . . . . . . . . 784
32.1.3 Conditional and Marginal Probabilities . . . . . . . . . 786
32.1.4 Average and Standard Deviation . . . . . . . . . . . . . 789
32.1.5 Counting: Permutations and Combinations . . . . . . . 791
32.2 Binomial Probability Distribution . . . . . . . . . . . . . . . . . 792
32.3PoissonDistribution ........................797
32.4 Continuous Random Variable . . . . . . . . . . . . . . . . . . . 801
32.4.1 TransformationofVariables................804
32.4.2 NormalDistribution ....................806
32.5Problems ..............................809
Bibliography 815
Index 817
Part I
Coordinates and Calculus

Chapter 1
Coordinate Systems
and Vectors
Coordinates and vectors—in one form or another—are two of the most
fundamental concepts in any discussion of mathematics as applied to physi-
cal problems. So, it is beneficial to start our study with these two concepts.
Both vectors and coordinates have generalizations that cover a wide vari-
ety of physical situations including not only ordinary three-dimensional space
with its ordinary vectors, but also the four-dimensional spacetime of relativity
with its so-called four vectors, and even the infinite-dimensional spaces used
in quantum physics with their vectors of infinite components. Our aim in this
chapteristoreviewtheordinary space and how it is used to describe physical
phenomena. To facilitate this discussion, we first give an outline of some of
the properties of vectors.
1.1 Vectors in a Plane and in Space
We start with the most common definition of a vector as a directed line
segment without regard to where the vector is located. In other words, a vector
is a directed line segment whose only important attributes are its direction
and its length. As long as we do not change these two attributes, the vector is
general properties
of vectors
not affected. Thus, we are allowed to move a vector parallel to itself without
changing the vector. Examples of vectors
1
are position r, displacement Δr,
velocity v,momentump, electric field E, and magnetic field B. The vector
that has no length is called the zero vector and is denoted by 0.
Vectors would be useless unless we could perform some kind of operation
on them. The most basic operation is changing the length of a vector. This
is accomplished by multiplying the vector by a real positive number. For
example, 3.2r is a vector in the same direction as r but 3.2 times longer. We
1
Vectors will be denoted by Roman letters printed in boldface type.
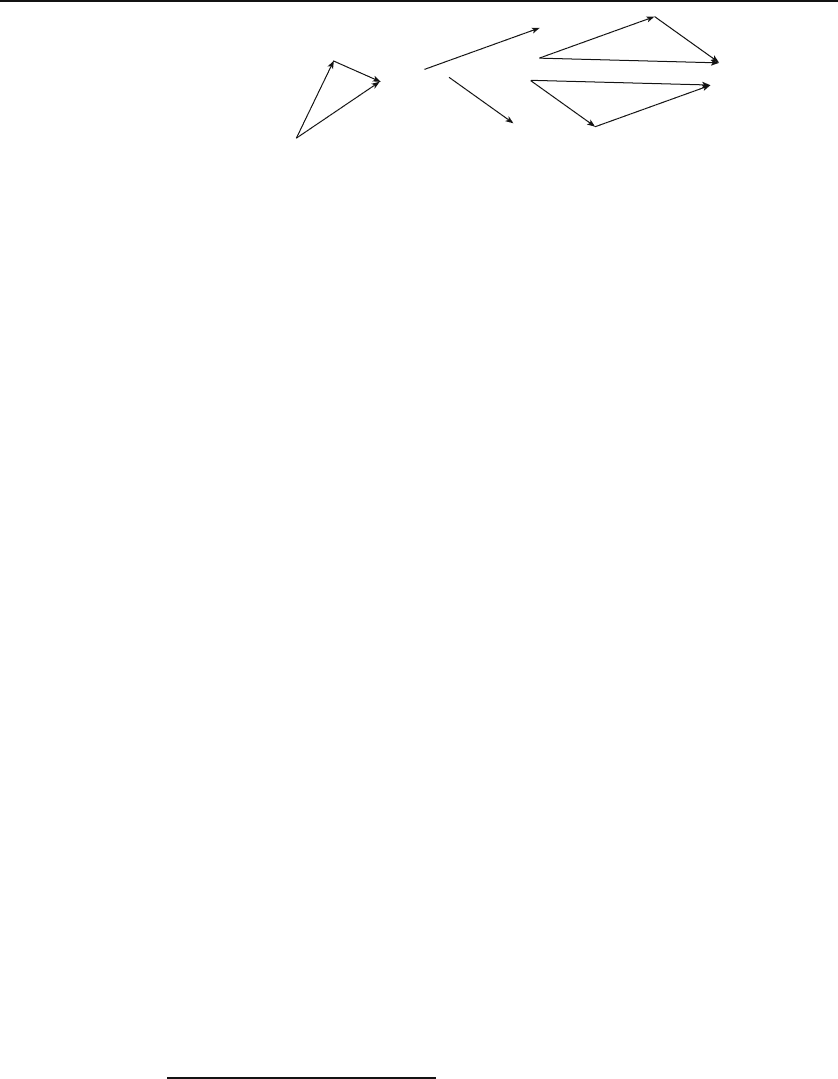
4 Coordinate Systems and Vectors
a
b
a
a
b
b
b
+ a
a
+ b
Δr
1
Δ
r
2
ΔR
=
Δ
r
1
+
Δr
2
(a) (b)
A
C
B
Figure 1.1: Illustration of the commutative law of addition of vectors.
can flip the direction of a vector by multiplying it by −1. That is, (−1) ×r =
−r is a vector having the same length as r but pointing in the opposite
direction. We can combine these two operations and think of multiplying a
vector by any real (positive or negative) number. The result is another vector
operations on
vectors
lyingalongthesamelineas the original vector. Thus, −0.732r is a vector
that is 0.732 times as long as r and points in the opposite direction. The zero
vector is obtained every time one multiplies any vector by the number zero.
Another operation is the addition of two vectors. This operation, with
which we assume the reader to have some familiarity, is inspired by the obvious
addition law for displacements. In Figure 1.1(a), a displacement, Δr
1
from
A to B is added to the displacement Δr
2
from B to C to give ΔR their
resultant, or their sum, i.e., the displacement from A to C:Δr
1
+Δr
2
=ΔR.
Figure 1.1(b) shows that addition of vectors is commutative: a + b = b + a.
It is also associative, a +(b + c)=(a + b)+c, i.e., the order in which you
add vectors is irrelevant. It is clear that a + 0 = 0 + a = a for any vector a.
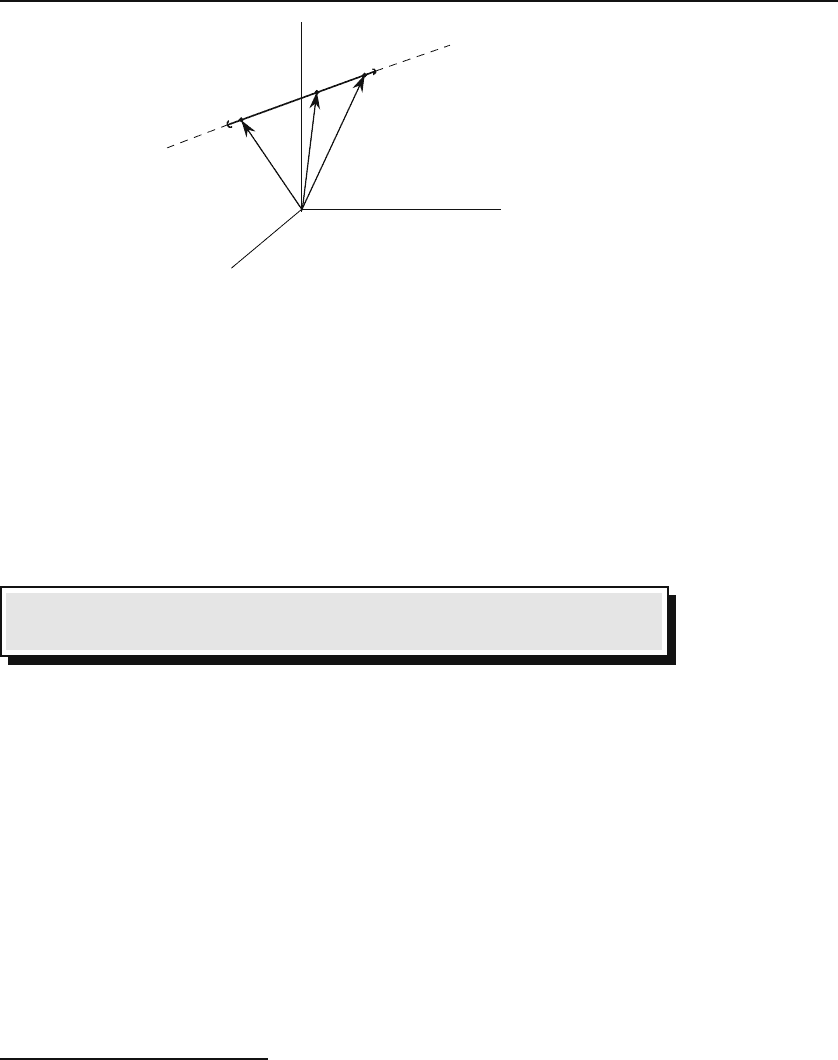
Example 1.1.1.
The parametric equation of a line through two given points
can be obtained in vector form by noting that any point in space defines a vector
whose components are the coordinates of the given point.
2
If the components of
the points P and Q in Figure 1.2 are, respectively, (p
x
,p
y
,p
z
)and(q
x
,q
y
,q
z
), then
we can define vectors p and q with those components. An arbitrary point X with
components (x, y, z) will lie on the line PQ if and only if the vector x =(x, y, z)
has its tip on that line. This will happen if and only if the vector joining P and X,
namely x − p, is proportional to the vector joining P and Q,namelyq − p.Thus,
for some real number t,wemusthavevector form of the
parametric
equation of a line
x − p = t(q − p)orx = t(q − p)+p.
This is the vector form of the equation of a line. We can write it in component
form by noting that the equality of vectors implies the equality of corresponding
components. Thus,
x =(q
x
− p
x
)t + p
x
,
y =(q
y
− p
y
)t + p
y
,
z =(q
z
− p
z
)t + p
z
,
which is the usual parametric equation for a line.
2
We shall discuss components and coordinates in greater detail later in this chapter. For
now, the knowledge gained in calculus is sufficient for our discussion.
1.1 Vectors in a Plane and in Space 5
O
P
Q
X
x
y
z
p
q
x
Figure 1.2: The parametric equation of a line in space can be obtained easily using
vectors.
There are some special vectors that are extremely useful in describing
physical quantities. These are the unit vectors. If one divides a vector
use of unit vectors
by its length, one gets a unit vector in the direction of the original vector.
Unit vectors are generally denoted by the symbol
ˆ
e with a subscript which
designates its direction. Thus, if we divided the vector a by its length |a| we
get the unit vector
ˆ
e
a
in the direction of a. Turning this definition around,
we have
Box 1.1.1. If we know the magnitude |a| of a vector quantity as well as
its direction
ˆ
e
a
, we can construct the vector: a = |a|
ˆ
e
a
.
This construction will be used often in the sequel.
The most commonly used unit vectors are those in the direction of coor-
unit vectors along
the x-, y-, and
z-axes
dinate axes. Thus
ˆ
e
x
,
ˆ
e
y
,and
ˆ
e
z
are the unit vectors pointing in the positive
directions of the x-, y-, and z-axes, respectively.
3
We shall introduce unit
vectors in other coordinate systems whenwediscussthosecoordinatesystems
later in this chapter.
1.1.1 Dot Product
The reader is no doubt familiar with the concept of dot product whereby
two vectors are “multiplied” and the result is a number. The dot product of
a and b is defined by
dot product
defined
a ·b ≡|a||b|cos θ, (1.1)
where |a| is the length of a, |b| is the length of b,andθ is the angle between
the two vectors. This definition is motivated by many physical situations.
3
These unit vectors are usually denoted by i, j,andk, a notation that can be confusing
when other non-Cartesian coordinates are used. We shall not use this notation, but adhere
to the more suggestive notation introduced above.
6 Coordinate Systems and Vectors
N
v
F
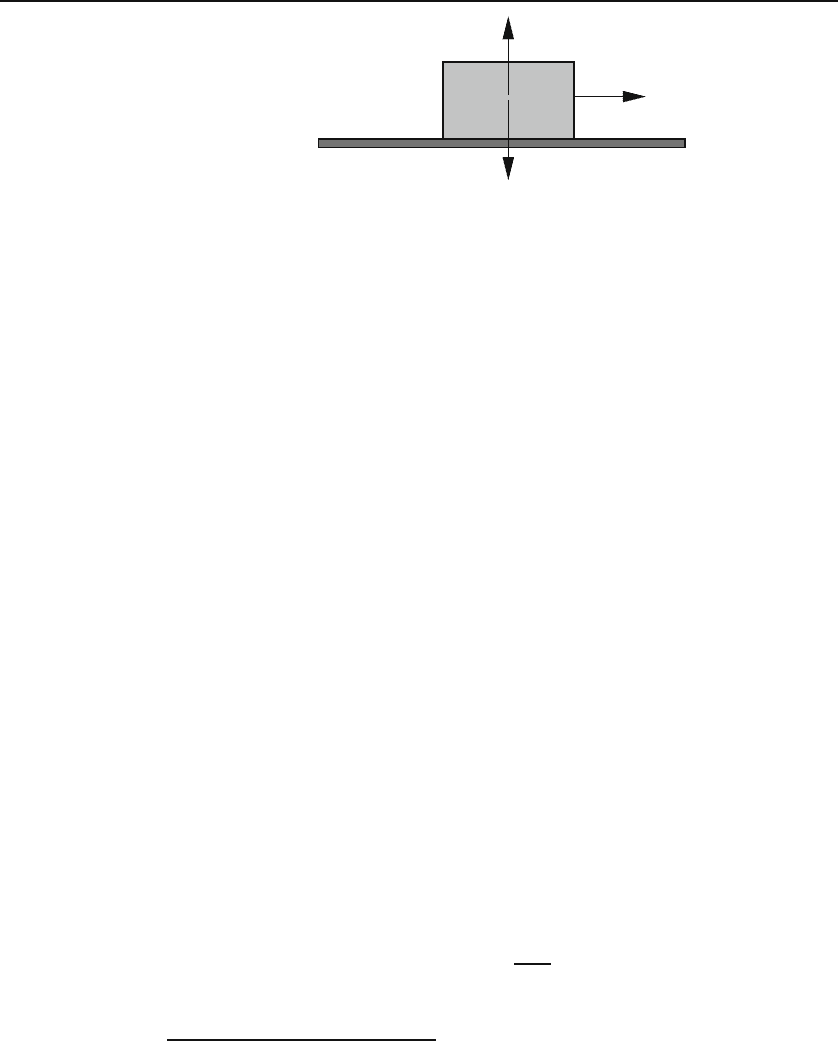
Figure 1.3: No work is done by a force orthogonal to displacement. If such a work
were not zero, it would have to be positive or negative; but no consistent rule exists to
assign a sign to the work.
The prime example is work which is defined as the scalar product of force and
displacement. The presence of cos θ ensures the requirement that the work
done by a force perpendicular to the displacement is zero. If this requirement
were not met, we would have the precarious situation of Figure 1.3 in which
the two vertical forces add up to zero but the total work done by them is
not zero! This is because it would be impossible to assign a “sign” to the
work done by forces being displaced perpendicular to themselves, and make
the rule of such an assignment in such a way that the work of F in the figure
cancels that of N. (The reader is urged to try to come up with a rule—e.g.,
assigning a positive sign to the work if the velocity points to the right of the
observer and a negative sign if it points to the observer’s left—and see that it
will not work, no matter how elaborate it may be!) The only logical definition
of work is that which includes a cos θ factor.
The dot product is clearly commutative, a · b = b · a.Moreover,itdis-
properties of dot
product
tributes over vector addition
(a + b) · c = a · c + b · c.
To see this, note that Equation (1.1) can be interpreted as the product of the
length of a with the projection of b along a. Now Figure 1.4 demonstrates
4
that the projection of a + b along c is the sum of the projections of a and b
along c (see Problem 1.2 for details). The third property of the inner product
is that a · a is always a positive number unless a is the zero vector in which
case a · a = 0. In mathematics, the collection of these three properties—
properties defining
the dot (inner)
product
commutativity, positivity, and distribution over addition—defines adot(or
inner) product on a vector space.
The definition of the dot product leads directly to a · a = |a|
2
or
|a| =
√
a ·a, (1.2)
whichisusefulincalculatingthelength of sums or differences of vectors.
4
Figure 1.4 appears to prove the distributive property only for vectors lying in the same
plane. However, the argument will be valid even if the three vectors are not coplanar.
Instead of dropping perpendicular lines from the tips of a and b, one drops perpendicular
planes.

1.1 Vectors in a Plane and in Space 7
A
B
O
a
b
a+b
c
Proj. of a
Proj. of b
Figure 1.4: The distributive property of the dot product is clearly demonstrated if we
interpret the dot product as the length of one vector times the projection of the other
vector on the first.
One can use the distributive property of the dot product to show that
if (a
x
,a
y
,a
z
)and(b
x
,b
y
,b
z
) represent the components of a and b along the
axes x, y,andz,then
dot product in
terms of
components
a ·b = a
x
b
x
+ a
y
b
y
+ a
z
b
z
. (1.3)
From the definition of the dot product, we can draw an important conclu-
sion. If we divide both sides of a · b = |a||b|cos θ by |a|,weget
a ·b
|a|
= |b|cos θ or
a
|a|
· b = |b|cos θ ⇒
ˆ
e
a
· b = |b|cos θ.
Noting that |b|cos θ is simply the projection of b along a, we conclude
ausefulrelationto
be used frequently
in the sequel
Box 1.1.2. To find the perpendicular projection of a vector b along
another vector a, take the dot product of b with
ˆ
e
a
, the unit vector along a.
Sometimes “component” is used for perpendicular projection. This is not
entirely correct. For any set of three mutually perpendicular unit vectors in
space, Box 1.1.2 can be used to find the components of a vector along the
three unit vectors. Only if the unit vectors are mutually perpendicular do
components and projections coincide.
1.1.2 Vector or Cross Product
Given two space vectors, a and b, we can find a third space vector c, called
the cross product of a and b, and denoted by c = a × b. The magnitude
cross product of
two space vectors
of c is defined by |c| = |a||b| sin θ where θ is the angle between a and b.
The direction of c is given by the right-hand rule:Ifa is turned to b (note
right-hand rule
explained
the order in which a and b appear here) through the angle between a and b,

8 Coordinate Systems and Vectors
a (right-handed) screw that is perpendicular to a and b will advance in the
direction of a × b. This definition implies that
a ×b = −b × a.
This property is described by saying that the cross product is antisymmet-
cross product is
antisymmetric
ric. The definition also implies that
a ·(a ×b)=b ·(a ×b)=0.
That is, a × b is perpendicular to both a and b.
5
The vector product has the following properties:
a ×(αb)=(αa) × b = α(a × b), a ×b = −b × a,
a ×(b + c)=a ×b + a × c, a ×a =0. (1.4)
Using these properties, we can write the vector product of two vectors in terms
of their components. We are interested in a more general result valid in other
coordinate systems as well. So, rather than using x, y,andz as subscripts for
unit vectors, we use the numbers 1, 2, and 3. In that case, our results can
cross product in
terms of
components
also be used for spherical and cylindrical coordinates which we shall discuss
shortly.
a ×b =(α
1
ˆ
e
1
+ α
2
ˆ
e
2
+ α
3
ˆ
e
3
) ×(β
1
ˆ
e
1
+ β
2
ˆ
e
2
+ β
3
ˆ
e
3
)
= α
1
β
1
ˆ
e
1
×
ˆ
e
1
+ α
1
β
2
ˆ
e
1
×
ˆ
e
2
+ α
1
β
3
ˆ
e
1
×
ˆ
e
3
+ α
2
β
1
ˆ
e
2
×
ˆ
e
1
+ α
2
β
2
ˆ
e
2
×
ˆ
e
2
+ α
2
β
3
ˆ
e
2
×
ˆ
e
3
+ α
3
β
1
ˆ
e
3
×
ˆ
e
1
+ α
3
β
2
ˆ
e
3
×
ˆ
e
2
+ α
3
β
3
ˆ
e
3
×
ˆ
e
3
.
But, by the last property of Equation (1.4), we have
ˆ
e
1
×
ˆ
e
1
=
ˆ
e
2
×
ˆ
e
2
=
ˆ
e
3
×
ˆ
e
3
=0.
Also, if we assume that
ˆ
e
1
,
ˆ
e
2
,and
ˆ
e
3
form a so-called right-handed set,
i.e., if
right-handed set
of unit vectors
ˆ
e
1
×
ˆ
e
2
= −
ˆ
e
2
×
ˆ
e
1
=
ˆ
e
3
,
ˆ
e
1
×
ˆ
e
3
= −
ˆ
e
3
×
ˆ
e
1
= −
ˆ
e
2
, (1.5)
ˆ
e
2
×
ˆ
e
3
= −
ˆ
e
3
×
ˆ
e
2
=
ˆ
e
1
,
then we obtain
a ×b =(α
2
β
3
− α
3
β
2
)
ˆ
e
1
+(α
3
β
1
− α
1
β
3
)
ˆ
e
2
+(α
1
β
2
− α
2
β
1
)
ˆ
e
3
5
This fact makes it clear why a × b is not defined in the plane. Although it is possible
to define a × b for vectors a and b lying in a plane, a × b will not lie in that plane (it
will be perpendicular to that plane). For the vector product, a and b (although lying in a
plane) must be considered as space vectors.

1.1 Vectors in a Plane and in Space 9
e
1
e
2
e
3
α
1
α
2
α
3
β
1
β
2
β
3
det
e
1
e
2
e
3
α
1
α
2
α
3
β
1
β
2
β
3
e
1
e
2
e
3
α
1
α
2
α
3
β
1
β
2
β
3
=
Figure 1.5: A 3 × 3 determinant is obtained by writing the entries twice as shown,
multiplying all terms on each slanted line and adding the results. The lines from upper
left to lower right bear a positive sign, and those from upper right to lower left a negative
sign.
which can be nicely written in a determinant form
6
cross product in
terms of the
determinant of
components
a ×b =det
⎛
⎝
ˆ
e
1
ˆ
e
2
ˆ
e
3
α
1
α
2
α
3
β
1
β
2
β
3
⎞
⎠
. (1.6)
Figure 1.5 explains the rule for “expanding” a determinant.
Example 1.1.2.
From the definition of the vector product and Figure 1.6(a),
we note that area of a
parallelogram in
terms of cross
product of its two
sides
|a × b| = area of the parallelogram defined by a and b.
So we can use Equation (1.6) to find the area of a parallelogram defined by two
vectors directly in terms of their components. For instance, the area defined by
a =(1, 1, −2) and b =(2, 0, 3) can be found by calculating their vector product
a × b =det
⎛
⎝
ˆ
e
1
ˆ
e
2
ˆ
e
3
11−2
20 3
⎞
⎠
=3
ˆ
e
1
− 7
ˆ
e
2
− 2
ˆ
e
3
,
and then computing its length
|a × b| =
3
2
+(−7)
2
+(−2)
2
=
√
62.
a
b
c
θ
θ
|a| cos θ
a
b
|a| sin θ
θ
b × c
(a) (b)
Figure 1.6: (a) The area of a parallelogram is the absolute value of the cross product of
the two vectors describing its sides. (b) The volume of a parallelepiped can be obtained
by mixing the dot and the cross products.
6
No knowledge of determinants is necessary at this point. The reader may consider (1.6)
to be a mnemonic device useful for remembering the components of a × b.

10 Coordinate Systems and Vectors
Example 1.1.3. The volume of a parallelepiped defined by three non-coplanar
vectors, a, b,andc,isgivenby|a ·(b × c)|. This can be seen from Figure 1.6(b),
where it is clear thatvolume of a
parallelepiped as a
combination of
dot and cross
products
volume = (area of base)(altitude) = |b × c|(|a|cos θ)=|(b × c) · a|.
The absolute value is taken to ensure the positivity of the area. In terms of compo-
nents we have
volume = |(b × c)
1
α
1
+(b × c)
2
α
2
+(b × c)
3
α
3
|
= |(β
2
γ
3
− β
3
γ
2
)α
1
+(β
3
γ
1
− β
1
γ
3
)α
2
+(β
1
γ
2
− β
2
γ
1
)α
3
|,
which can be written in determinant form asvolume of a
parallelepiped as
the determinant of
the components of
its side vectors
volume = |a · (b × c)| =
det
⎛
⎝
α
1
α
2
α
3
β
1
β
2
β
3
γ
1
γ
2
γ
3
⎞
⎠
.
Note how we have put the absolute value sign around the determinant of the matrix,
so that the area comes out positive.
Historical Notes
The concept of vectors as directed line segments that could represent velocities,
forces, or accelerations has a very long history. Aristotle knew that the effect of two
forces acting on an object could be described by a single force using what is now
called the parallelogram law. However, the real development of the concept took an
unexpected turn in the nineteenth century.
With the advent of complex numbers and the realization by Gauss, Wessel, and
especially Argand, that they could be represented by points in a plane, mathemati-
cians discovered that complex numbers could be used to study vectors in a plane.
A complex number is represented by a pair
7
of real numbers—called the real and
imaginary parts of the complex number—which could be considered as the two
components of a planar vector.
This connection between vectors in a plane and complex numbers was well es-
tablished by 1830. Vectors are, however, useful only if they are treated as objects
in space. After all, velocities, forces, and accelerations are mostly three-dimensional
objects. So, the two-dimensional complex numbers had to be generalized to three
dimensions. This meant inventing ways of adding, subtracting, multiplying, and
dividing objects such as (x, y, z).
The invention of a spatial analogue of the planar complex numbers is due to
William R. Hamilton. Next to Newton, Hamilton is the greatest of all English
William R.
Hamilton
1805–1865
mathematicians, and like Newton he was even greater as a physicist than as a
mathematician. At the age of five Hamilton could read Latin, Greek, and Hebrew.
At eight he added Italian and French; at ten he could read Arabic and Sanskrit,
and at fourteen, Persian. A contact with a lightning calculator inspired him to
study mathematics. In 1822 at the age of seventeen and a year before he entered
Trinity College in Dublin, he prepared a paper on caustics which was read before the
Royal Irish Academy in 1824 but not published. Hamilton was advised to rework
and expand it. In 1827 he submitted to the Academy a revision which initiated the
science of geometrical optics and introduced new techniques in analytical mechanics.
7
See Chapter 18.
