Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

1.3 Vectors in Diﬀerent Coordinate Systems 21

One of the great advantages of vectors is their ability to express results Physical laws

ought to be

coordinate

independent!

independent of any speciﬁc coordinate systems. Physical laws are always

coordinate-independent. For example, when we write F = ma both F and a

could be expressed in terms of Cartesian, spherical, cylindrical, or any other

convenient coordinate system. This independence allows us the freedom to

choose the coordinate systems most convenient for the problem at hand. For

example, it is extremely diﬃcult to solve the planetary motions in Cartesian

coordinates, while the use of spherical coordinates facilitates the solution of

the problem tremendously.

Example 1.3.1.

We can express the coordinates of the center of mass (CM) of center of mass

a collection of particles in terms of their position vectors.

Thus, if r denotes the

position vector of the CM of the collection of N mass points, m

,...,m

with

respective position vectors r

, r

,...,r

relative to an origin O,then

r =

+ m

+ ···+ m

+ m

+ ···+ m



k=1

, (1.20)

where M =



k=1

is the total mass of the system. One can also think of Equation

(1.20) as a vector equation. To ﬁnd the component equations in a coordinate system,

one needs to pick a ﬁxed point (say the origin), a set of unit vectors at that point

(usually the unit vectors along the axes of some coordinate system), and substitute

the components of r

along those unit vectors to ﬁnd the components of r along the

unit vectors.



1.3.1 Fields and Potentials

The distributive property of the dot product and the fact that the unit vectors

of the bases in all coordinate systems are mutually perpendicular can be used

to derive the following:

dot product in

terms of

components in the

three coordinate

systems

a ·b = a

+ a

(Cartesian),

a ·b = a

+ a

(cylindrical), (1.21)

a ·b = a

+ a

(spherical).

The ﬁrst of these equations is the same as (1.3 ).

It is important to keep in mind that the components are to be expressed

in the same set of unit vectors. This typically means setting up mutually per-

pendicular unit vectors (an orthonormal basis) at a single point and resolving

all vectors along those unit vectors.

The dot product, in various forms and guises, has many applications in

physics. As pointed out earlier, it was introduced in the deﬁnition of work,

but soon spread to many other concepts of physics. One of the simplest—and

most important—applications is its use in writing the laws of physics in a

coordinate-independent way.

This implies that the equation is most useful only when Cartesian coordinates are

used, because only for these coordinates do the components of the position vector of a

point coincide with the coordinates of that point.

We assume that the reader is familiar with the symbol



simply as a summation

symbol. We shall discuss its properties and ways of manipulating it in Chapter 9.

22 Coordinate Systems and Vectors

(x, y, z)

Figure 1.14: The diagram illustrating the electrical force when one charge is at the

origin.

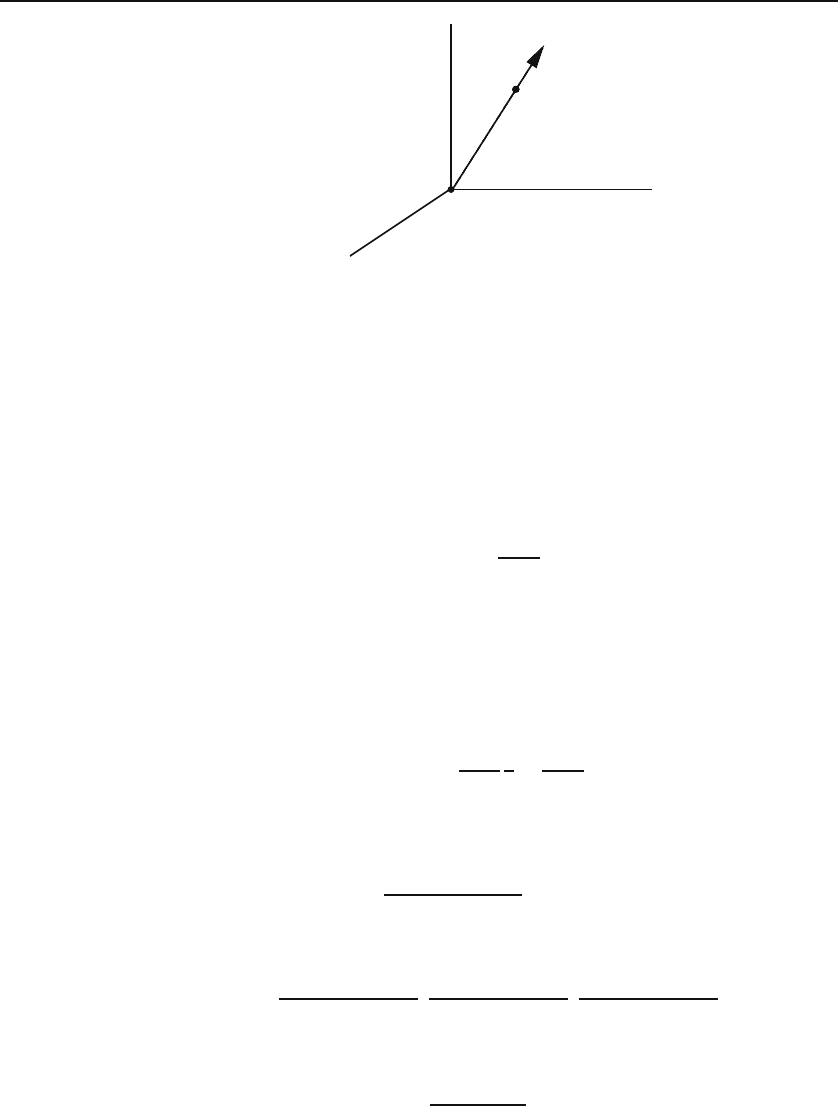
Example 1.3.2. A point charge q is situated at the origin. A second charge q



located at (x, y, z) as shown in Figure 1.14. We want to express the electric force

on q



in Cartesian, spherical, and cylindrical coordinate systems.

We know that the electric force, as given by Coulomb’s law, lies along the line

joining the two charges and is either attractive or repulsive according to the signs

of q and q



. All of this information can be summarized in the formulaCoulomb’s law



(1.22)

where k

=1/(4π

) ≈ 9 ×10

in SI units. Note that if q and q



are unlike, qq



< 0

and F



is opposite to

, i.e., it is attractive. On the other hand, if q and q



are of

the same sign, qq



> 0andF



is in the same direction as

, i.e., repulsive.

Equation (1.22) expresses F



in spherical coordinates. Thus, its components in

terms of unit vectors at q



are





, 0, 0



. To get the components in the other

coordinate systems, we rewrite (1.22). Noting that

= r/r,wewrite



r. (1.23)

For Cartesian coordinates we use (1.12) to obtain r

=(x

)

3/2

. Substituting

this and (1.17) in (1.23) yields



+ y

+ z

)

3/2

+ y

+ z

Therefore, the components of F



in Cartesian coordinates are





+ y

+ z

)

3/2



+ y

+ z

)

3/2



+ y

+ z

)

3/2



Finally, using (1.10) and (1.19) in (1.23), we obtain



(ρ

+ z

)

3/2

(ρ

+ z

1.3 Vectors in Diﬀerent Coordinate Systems 23

−

Figure 1.15: The displacement vector between P

and P

is the diﬀerence between

their position vectors.

Thus the components of F



along the cylindrical unit vectors constructed at the

location of q



are





(ρ

+ z

)

3/2

, 0,



(ρ

+ z

)

3/2





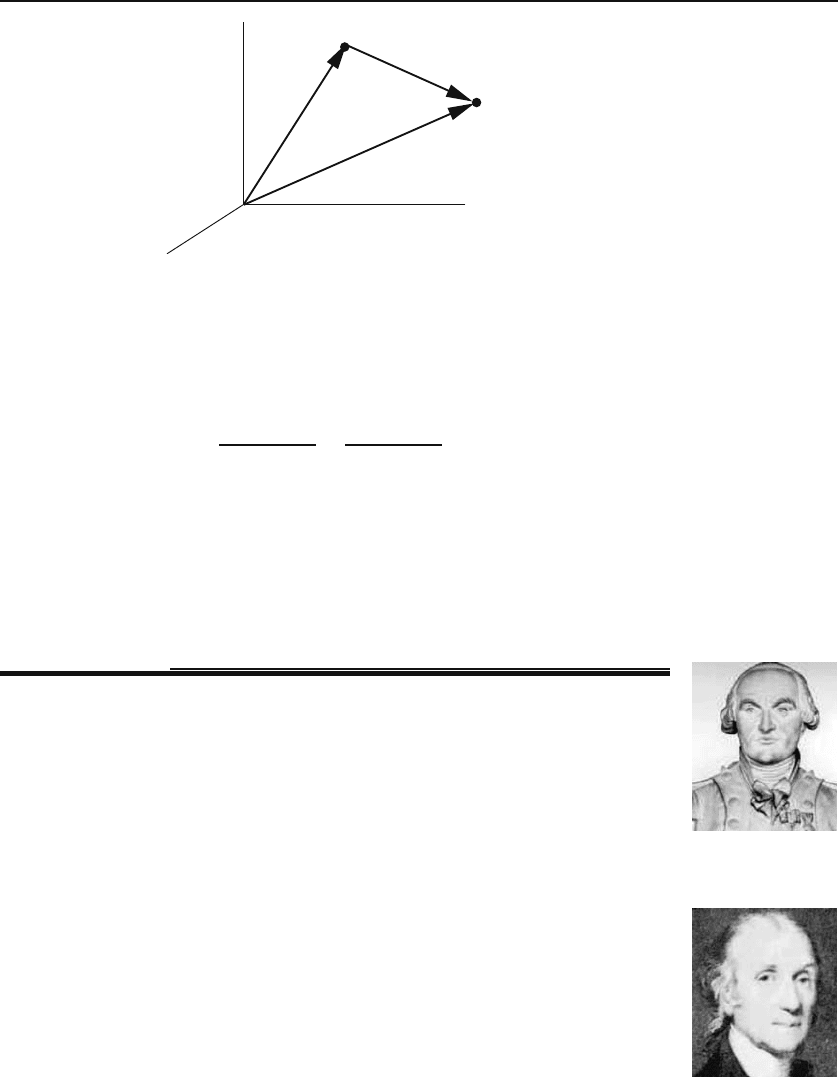
Since r gives the position of a point in space, one can use it to write

the distance between two points P

and P

with position vectors r

and r

Figure 1.15 shows that r

−r

is the displacement vector from P

to P

.The

importance of this vector stems from the fact that many physical quantities

are functions of distances between point particles, and r

−r

is a concise way

of expressing this distance. The following example illustrates this.

Historical Notes

During the second half of the eighteenth century many physicists were engaged in a

quantitative study of electricity and magnetism. Charles Augustin de Coulomb,

who developed the so-called torsion balance for measuring weak forces, is credited

with the discovery of the law governing the force between electrical charges.

Coulomb was an army engineer in the West Indies. After spending nine years

there, due to his poor health, he returned to France about the same time that the

French Revolution began, at which time he retired to the country to do scientiﬁc

Charles Coulomb

1736–1806

research.

Beside his experiments on electricity, Coulomb worked on applied mechanics,

structural analysis, the fracture of beams and columns, the thrust of arches, and the

thrust of the soil.

At about the same time that Coulomb discovered the law of electricity, there

lived in England a very reclusive character named Henry Cavendish.Hewas

born into the nobility, had no close friends, was afraid of women, and disinterested

in music or arts of any kind. His life revolved around experiments in physics and

chemistry that he carried out in a private laboratory located in his large mansion.

During his long life he published only a handful of relatively unimportant pa-

pers. But after his death about one million pounds sterling were found in his bank

Henry Cavendish

1731–1810

account and twenty bundles of notes in his laboratory. These notes remained in

the possession of his relatives for a long time, but when they were published one

24 Coordinate Systems and Vectors

hundred years later, it became clear that Henry Cavendish was one of the greatest

experimental physicists ever. He discovered all the laws of electric and magnetic

interactions at the same time as Coulomb, and his work in chemistry matches that

of Lavoisier. Furthermore, he used a torsion balance to measure the universal grav-

itational constant for the ﬁrst time, and as a result was able to arrive at the exact

mass of the Earth.

Example 1.3.3. Coulomb’s law for two arbitrary charges

Suppose there are point charges q

at P

and q

at P

. Let us write the force exerted

on q

by q

. The magnitude of the force is

where d =

is the distance between the two charges. We use d because the

usual notation r has special meaning for us: it is one of the coordinates in spherical

systems. If we multiply this magnitude by the unit vector describing the direction

of the force, we obtain the full force vector (see Box 1.1.1). But, assuming repulsion

for the moment, this unit vector is

− r

≡

Also, since d = |r

− r

|,wehave

− r

orCoulomb’s law

when charges are

arbitrarily located

− r

). (1.24)

Although we assumed repulsion, we see that (1.24) includes attraction as well. In-

deed, if q

< 0, F

is opposite to r

−r

, i.e., F

is directed from P

to P

.Since

is the force on q

by q

,thisisanattraction. We also note that Newton’s third

law is included in (1.24):

− r

)=−F

because r

− r

= −(r

− r

)and|r

− r

| = |r

− r

We can also write the gravitational force immediatelyvector form of

gravitational force

= −

− r

), (1.25)

where m

and m

are point masses and the minus sign is introduced to ensure

attraction.



Now that we have expressions for electric and gravitational forces, we can

obtain the electric ﬁeld of a point charge and the gravitational ﬁeld of a point

mass. First recall that the electric ﬁeld at a point P is deﬁned to be the

force on a test charge q located at P divided by q. Thusifwehaveacharge

,atP

with position vector r

and we are interested in its ﬁelds at P with

1.3 Vectors in Diﬀerent Coordinate Systems 25

position vector r, we introduce a charge q at r and calculate the force on q

from Equation (1.24):

|r − r

(r − r

Dividing by q gives

electric ﬁeld of a

point charge

|r − r

(r − r

), (1.26)

where we have given the ﬁeld the same index as the charge producing it.

The calculation of the gravitational ﬁeld follows similarly. The result is

= −

|r − r

(r − r

). (1.27)

In (1.26) and (1.27), P is called the ﬁeld point and P

the source point. ﬁeld point and

source point

Note that in both expressions, the ﬁeld position vector comes ﬁrst.

If there are several point charges (or masses) producing an electric (gravita-

tional) ﬁeld, we simply add the contributions from each source. The principle

superposition

principle explained

behind this procedure is called the superposition principle.Itisaprinci-

ple that “seems” intuitively obvious, but upon further reﬂection its validity

becomes surprising. Suppose a charge q

produces a ﬁeld E

around itself.

Now we introduce a second charge q

which, far away and isolated from any

other charges, produced a ﬁeld E

around itself. It is not at all obvious that

once we move these charges together, the individual ﬁelds should not change.

After all, this is not what happens to human beings! We act completely dif-

ferently when we are alone than when we are in the company of others. The

presence of others drastically changes our individual behaviors. Nevertheless,

charges and masses, unfettered by any social chains, retain their individuality

and produce ﬁelds as if no other charges were present.

It is important to keep in mind that the superposition principle applies

only to point sources. For example, a charged conducting sphere will not

produce the same ﬁeld when another charge is introduced nearby, because the

presence of the new charge alters the charge distribution of the sphere and

indeed does change the sphere’s ﬁeld. However each individual point charge

(electron) on the sphere, whatever location on the sphere it happens to end

up in, will retain its individual electric ﬁeld.

Going back to the electric ﬁeld, we can write

E = E

+ E

+ ···+ E

for n point charges q

,...,q

(see Figure 1.16). Substituting from (1.26),

with appropriate indices, we obtain

E =

|r − r

(r − r

|r − r

(r − r

)+···+

|r − r

(r − r

)

or, using the summation symbol, we obtain

The superposition principle, which in the case of electrostatics and gravity is needed

to calculate the ﬁelds of large sources consisting of many point sources, becomes a vital

pillar upon which quantum theory is built and by which many of the strange phenomena

of quantum physics are explained.

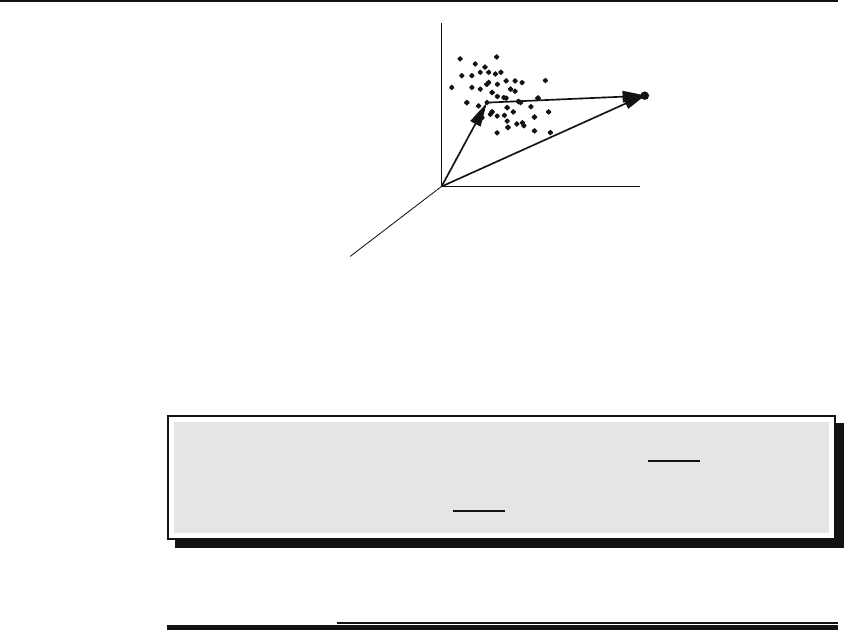
26 Coordinate Systems and Vectors

r – r

Figure 1.16: The electrostatic ﬁeld of N point charges is the sum of the electric ﬁelds

of the individual charges.

Box 1.3.5. The electric ﬁeld of n point charges q

,...,q

,lo-

cated at position vectors r

, r

,...,r

is E =



i=1

|r−r

(r − r

), and

the analogous expression for the gravitational ﬁeld of n point masses

,...,m

is g = −



i=1

|r−r

(r − r

Historical Notes

The concept of force has a fascinating history which started in the works of Galileo

around the beginning of the seventeenth century, mathematically formulated and

precisely deﬁned by Sir Isaac Newton in the second half of the seventeenth century,

revised and redeﬁned in the form of ﬁelds by Michael Faraday and James Maxwell

in the mid nineteenth century, and ﬁnally brought to its modern quantum ﬁeld

theoretical form by Dirac, Heisenberg, Feynman, Schwinger, and others by the mid

twentieth century.

Newton, in his theory of gravity, thought of gravitational force as “action-notion of ﬁeld

elaborated at-a-distance,” an agent which aﬀects something that is “there” because of the

inﬂuence of something that is “here.” This kind of interpretation of force had both

philosophical and physical drawbacks. It is hard to accept a ghostlike inﬂuence

on a distant object. Is there an agent that “carries” this inﬂuence? What is this

agent, if any? Does the inﬂuence travel inﬁnitely fast? If we remove the Sun from

the Solar System would the Earth and other planets “feel” the absence of the Sun

immediately?

These questions, plus others, prompted physicists to come up with the idea of a

ﬁeld. According to this interpretation, the Sun, by its mere presence, creates around

itself an invisible three dimensional “sheet” such that, if any object is placed in this

sheet, it feels the gravitational force. The reason that planets feel the force of gravity

of the Sun is because they happen to be located in the gravitational ﬁeld of the Sun.

The reason that an apple falls to the Earth is because it is in the gravitational ﬁeld

of the Earth and not due to some kind of action-at-a-distance ghost.

1.3 Vectors in Diﬀerent Coordinate Systems 27

Therefore, according to this concept, the force acts on an object here,because

there exists a ﬁeld right here. And force becomes a local concept. The ﬁeld con-

cept removes the diﬃculties associated with action-at-a-distance. The “agent” that

transmits the inﬂuence from the source to the object, is the ﬁeld. If the Sun is stolen

from the solar system, the Earth will not feel the absence of the Sun immediately.

It will receive the information of such cosmic burglary after a certain time-lapse

corresponding to the time required for the disturbance to travel from the Sun to the

Earth. We can liken such a disturbance (disappearance of the Sun) to a disturbance

in the smooth water of a quiet pond (by dropping a stone into it). Clearly, the dis-

turbance travels from the source (where the stone was dropped) to any other point

with a ﬁnite speed, the speed of the water waves.

The concept of a ﬁeld was actually introduced ﬁrst in the context of electricity

and magnetism by Michael Faraday as a means of “visualizing” electromagnetic

eﬀects to replace certain mathematical ideas for which he had little talent. However,

in the hands of James Maxwell, ﬁelds were molded into a physical entity having an

existence of their own in the form of electromagnetic waves to be produced in 1887

by Hertz and used in 1901 by Marconi in the development of radio.

A concept related to that of ﬁelds is potential which is closely tied to the potential

work done by the ﬁelds on a charge (in the case of electrostatics) or a mass

(in the case of gravity). It can be shown

that the gravitational potential

Φ(r)atr,ofn point masses, is given by

Φ(r)=−



i=1

|r − r

(1.28)

and that of n point charges by

Φ(r)=



i=1

|r − r

. (1.29)

Note that in both cases, the potential goes to zero as r goes to inﬁnity. This

has to do with the choice of the location of the zero of potential, which we

have chosen to be the point at inﬁnity in Equations (1.28) and (1.29).

Example 1.3.4.

The electric charges q

,andq

are located at Cartesian

(a, 0, 0), (0,a,0), (−a, 0, 0), and (0, −a, 0), respectively. We want to ﬁnd the electric

ﬁeld and the electrostatic potential at an arbitrary point on the z-axis. We note

that

= a

, r

= a

, r

= −a

, r

= −a

, r = z

so that

r − r

= −a

+ z

, r − r

= −a

+ z

r − r

= a

+ z

, r − r

= a

+ z

See Chapter 14 for details.

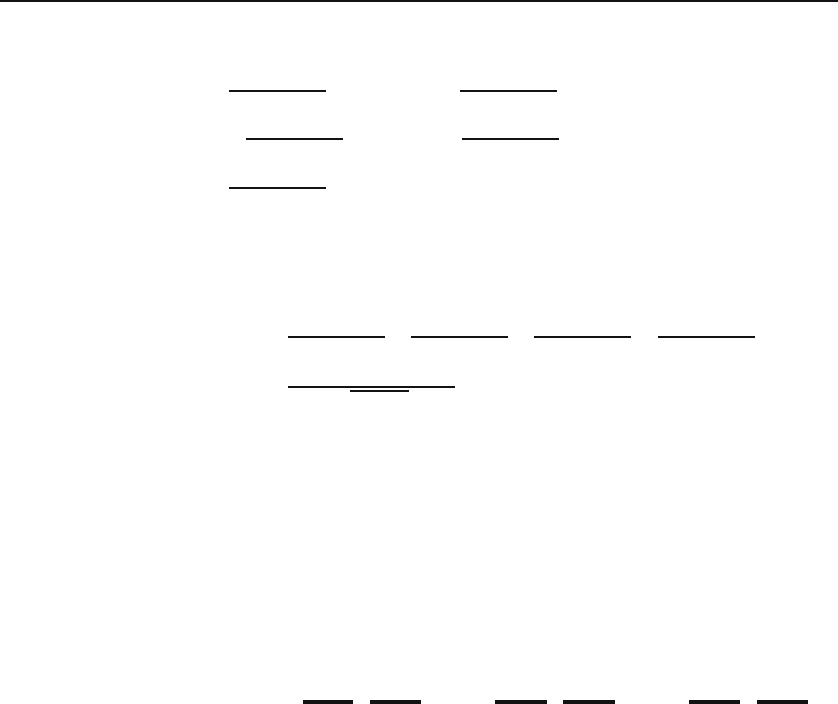
28 Coordinate Systems and Vectors

and |r − r

=(a

+ z

)

3/2

for all i. The electric ﬁeld can now be calculated using

Box 1.3.5:

E =

+ z

)

3/2

(−a

+ z

)

3/2

(−a

+ z

)

+ z

)

3/2

+ z

)

3/2

+ z

)

+ z

)

3/2

[(−aq

+ aq

)

+(−aq

+ aq

)

+(q

+ q

] .

It is interesting to note that if the sum of all charges is zero, the z-component of

the electric ﬁeld vanishes at all points on the z-axis. Furthermore, if, in addition,

= q

and q

= q

, there will be no electric ﬁeld at any point on the z-axis.

The potential is obtained similarly:

Φ=

+ z

)

1/2

+ z

)

1/2

+ z

)

1/2

+ z

)

1/2

+ q

)

√

+ z

So, the potential is zero at all points of the z-axis, as long as the total charge

is zero.



1.3.2 Cross Product

The unit vectors in the three coordinate systems are not only mutually perpen-

dicular, but in the order in which they are given, they also form a right-handed

set [see Equation (1.5)]. Therefore, we can use Equation (1.6) and write

a ×b =det

⎛

⎝

⎞

⎠



 

in Cartesian CS

=det

⎛

⎝

⎞

⎠



 

in cylindrical CS

=det

⎛

⎝

⎞

⎠



 

in spherical CS

(1.30)

Two important prototypes of the concept of cross product are angular

momentum and torque. A particle moving with instantaneous linear mo-

mentum p relative to an origin O has instantaneous angular momentum

L = r × p if its instantaneous position vector with respect to O is r.In

Figure 1.17 we have shown r, p,andr × p. Similarly, if the instantaneous

force on the above particle is F, then the instantaneous torque acting on it is

T = r × F.

If there are more than one particle we simply add the contribution of

individual particles. Thus, the total angular momentum L of N particles and

angular

momentum and

torque as

examples of cross

products

the total torque T acting on them are

L =



k=1

× p

and T =



k=1

× F

, (1.31)

where r

is the position of the kth particle, p

its instantaneous momentum,

and F

the instantaneous force acting on it.

1.3 Vectors in Diﬀerent Coordinate Systems 29

r × p

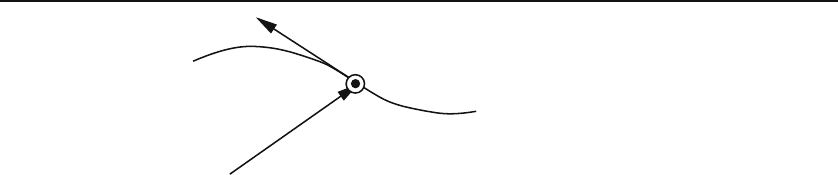
Figure 1.17: Angular momentum of a moving particle with respect to the origin O.

The circle with a dot in its middle represents a vector pointing out of the page. It is

assumed that r and p lie in the page.

Example 1.3.5. In this example, we show that the torque on a collection of three

particles is caused by external forces only. The torques due to the internal forces

add up to zero. The generalization to an arbitrary number of particles will be done

in Example 9.2.1 when we learn how to manipulate summation symbols.

For N = 3, the second formula in Equation (1.31) reduces to

T = r

× F

+ r

× F

+ r

× F

Each force can be divided into an external part and an internal part, the latter being

the force caused by the presence of the other particles. So, we have

= F

(ext)

+ F

= F

(ext)

+ F

= F

(ext)

+ F

where F

is the force on particle 1 exerted by particle 2, etc. Substituting in the

above expression for the torque, we get

T = r

× F

(ext)

+ r

× F

(ext)

+ r

× F

(ext)

+ r

× F

+ r

× F

+ r

× F

+ r

× F

+ r

× F

+ r

× F

= T

(ext)

+(r

− r

) × F

+(r

− r

) × F

+(r

− r

) × F

whereweusedthethirdlawofmotion: F

= −F

, etc. Now we note that the

internal force between two particles, 1 and 2 say, is along the line joining them, i.e.,

along r

− r

. It follows that all the cross products in the last line of the equation

above vanish and we get T = T

(ext)



We have already seen that multiplying avectorbyanumbergives another

vector. A physical example of this is electric force which is obtained by multi-

plying electric ﬁeld by electric charge. In fact we divided the electric force by

charge to get the electric ﬁeld. Historically, it was the law of the force which

from electric ﬁeld

to electric force

was discovered ﬁrst and then the concept of electric ﬁeld was deﬁned. We have

also seen that one can get a new vector by cross-multiplying two vectors.The

rule of this kind of multiplication is, however, more complicated. It turns out

30 Coordinate Systems and Vectors

that the magnetic force is related to the magnetic ﬁeld via such a cross multi-

plication. What is worse is that the magnetic ﬁeld is also related to its source

(electric charges in motion) via such a product. Little wonder that magnetic

phenomena are mathematically so much more complicated than their electric

counterparts. That is why in the study of magnetism, one ﬁrst introduces

the concept of magnetic ﬁeld and how it is related to the motion of charges

producing it, and then the force of this ﬁeld on moving charges.

Example 1.3.6.

Achargeq, located instantaneously at the origin, is moving

with velocity v relative to P [see Figure 1.18(a)]. Assuming that |v| is much smaller

than the speed of light, the instantaneous magnetic ﬁeld at P due to q is given by

B =

q v ×

,or,using

= r/r,byB =

q v × r

.Thisisasimpleversionofmagnetic ﬁeld of a

moving charge or

Biot–Savart law

a more general formula known as the Biot–Savart law. In the above relations, k

is the analog of k

in the electric case.

If we are interested in the magnetic ﬁeld when q is located at a point other

than the origin, we replace r with the vector from the instantaneous location of the

moving charge to P . This is shown in Figure 1.18(b), where the vector from q

P is to replace r in the above equation. More speciﬁcally, we have

× (r − r

)

|r − r

. (1.32)

If there are N charges, the total magnetic ﬁeld will be

B =



k=1

× (r − r

)

|r − r

, (1.33)

where we have used the superposition principle.



When a charge q moves with velocity v in a magnetic ﬁeld B, it experiences

a force given by

magnetic force on

amovingcharge.

F = qv × B. (1.34)

It is instructive to write the magnetic force exerted by a charge q

moving

with velocity v

on a second charge q

moving with velocity v

.Weleavethis

as an exercise for the reader.

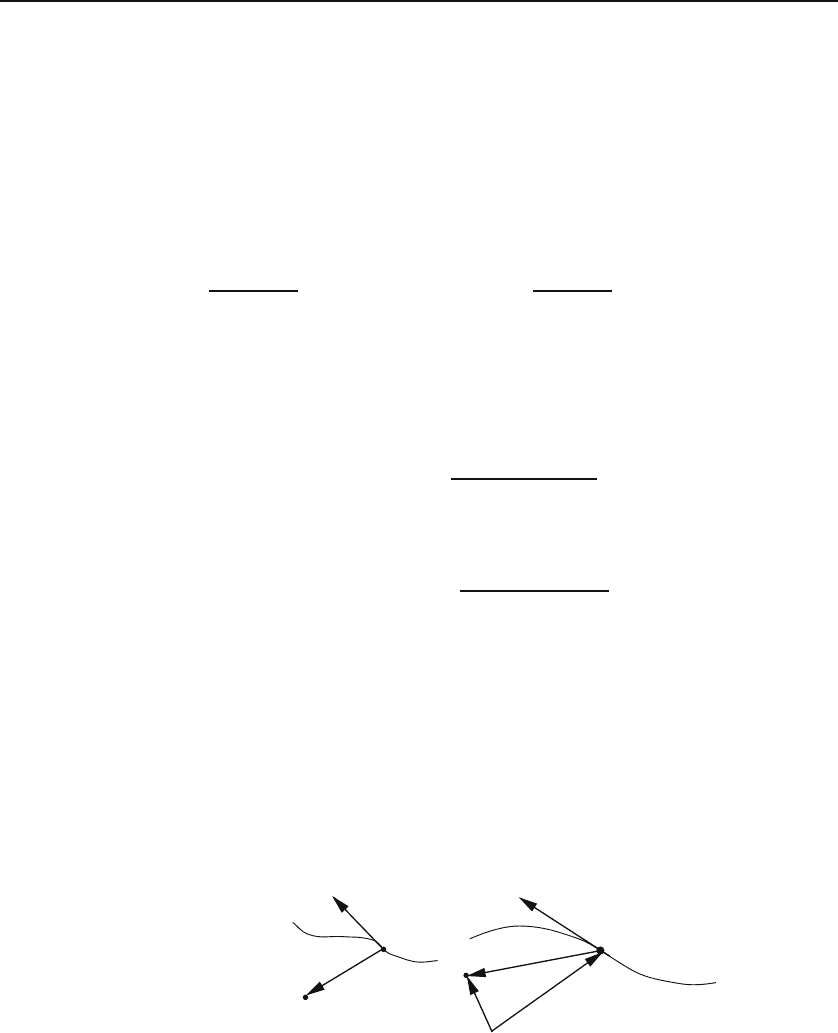
(b)O

(a)

r −

Figure 1.18: The (instantaneous) magnetic ﬁeld at P of a moving point charge (a)

when P is at the origin, and (b) when P is diﬀerent from the origin. The ﬁeld points

out of the page for the conﬁguration shown.