Hammond C. The Basics of Crystallography and Diffraction

Подождите немного. Документ загружается.

294 Electron diffraction and its applications

CrN(fcc) Fe

C(orthorhombic) (Cr,Fe)

(hexagonal)

a = 4.14 Å a = 4.524 Å a = 13.982 Å

b = 5.088 Å c = 4.506 Å

c = 6.741 Å

hkl

/Å hkl d

hkl

/Å hkl d

hkl

/Å hkl

2.39 111 6.742 001 12.108 01

2.07 200 5.088 010 6.991 11

1.46 220 4.524 100 6.054 02

1.25 311 4.061 011 4.576 12

1.20 222 3.757 101 4.506 0001

1.04 400 3.381 110 4.223 01

0.950 331 3.371 002 4.036 03

0.926 420 3.022 111 3.878 11

0.845 422 2.810 012 3.615 02

0.800 511 2.703 102 3.495 13

2.544 020 3.358 13

2.387 112 3.211 12

2.380 021 3.027 04

2.262 200 3.006 03

2.247 003 2.777 23

2.218 120 2.767 22

2.107 121 2.692 13

2.067 210 2.642 14

2.031 022 2.512 04

2.013 103 2.421 05

1.976 211 2.364 23

1.872 113 2.330 23

1.588 130 2.288 24

Fig. 11.19. A selected area electron diffraction pattern of a thin foil of a quenched and tempered steel

showing reﬂections from Fe

C precipitates in a single crystallographic orientation (weak spots) and

two twin-related orientations of the ferrite (α-Fe) matrix (strong spots). (Photograph by courtesy of

Dr. D. H. Jack.)

Exercises 295

11.5 Given the lattice parameter of aluminium a = 4.041 Å, ﬁnd the camera constant in Fig. 11.6.

11.6 Figure 11.19 is a selected area electron diffraction pattern of a thin foil of a steel (Fe,

1.3% Mn, 0.5% Mo, 0.7% Ni, 0.2% Cr, 0.2% C) which has been quenched from 1300

◦

and tempered at 615

◦

C. The microstructure consists of a matrix of tempered martensite

(α-Fe, bcc) and particles of cementite, iron carbide, Fe

C. The pattern includes α-Fe (strong

spots) and Fe

C (weak spots). Index the patterns and determine the orientation relationship

between α-Fe and Fe

C. The camera constant λL = 36 Å mm.

(Hint: A list of d

hkl

-spacings for α-Fe should be worked out given a

α-Fe

= 2.866 Å and

given the condition for allowed reﬂections for the Cubic I lattice (Table A6.2). The d

hkl

spacings for Fe

C are given in Exercise 11.4. Notice that the α-Fe pattern also consists of

two twin-related variants (see Fig. 7.17(a) for the analogous case in the diffraction of light.)

11.7 Draw the diamond-cubic pattern of germanium atoms in a 110projection (see Fig. 1.36(a))

and show that the pattern corresponds precisely with the high resolution TEM ‘dumbbell’

image (Fig. 11.15). Given that the lattice parameter a of germanium is 0.566 nm, calcu-

late the separation of the tetrahedrally coordinated atoms and their apparent ‘dumbbell’

separation in the 110 projection.

The stereographic projection

and its uses

12.1 Introduction

In Chapter 6 we showed how both the orientations and the d

hkl

spacings of planes could

be represented in terms of reciprocal lattice vectors and how these vectors could be used

to determine the angles between planes and to specify zones and zone axes. We now

need a method of representing the planes or faces in a crystal ‘all at once’ so that we can

recognize the zones to which they belong and determine the angles between them without

the need for repetitive calculations. The ‘crystal drawings’such as Fig. 5.7 are obviously

inadequate in this respect; half of the crystal faces are ‘hidden from view’ and we can

only recognize zones with difﬁculty by looking for the parallel lines of intersections

between the (visible) faces. The stereographic projection provides an important method

of overcoming these difﬁculties. It is similar to the reciprocal lattice construction in that

in both cases planes or faces are represented by their normals.

The stereographic projection is a very ancient geometrical technique; it originated in

the second century A.D. in the work of the Alexandrian astronomer Claudius Ptolemy

who used it as a means of representing the stars on the heavenly sphere. The original

Greek manuscript is lost, but the work comes down to us in a sixteenth-century Latin

translation from an Arabic commentary entitled The Planispherium. The stereographic

projection was ﬁrst applied to crystallography in the work of F. E. Neumann

∗

and was

further developed by W. H. Miller.

∗

The geometry of the stereographic projection may be described very simply. First,

the crystal is imagined to be at the centre of a sphere (the stereographic sphere); the

normals to the crystal faces are imagined to radiate out from the centre and to intersect

the sphere in an array of points. Each point on the sphere therefore represents a crystal

face or plane (and is labelled with the appropriate Miller index) just as a ‘point’ on the

surface of the Earth represents a town or city. The (angular) distance between two points

is equal to the angle between the corresponding planes and is determined in the same

way that we ﬁnd the angular distance between, say, Bangkok and New York: we take

our private aeroplane and, uninhibited by Trafﬁc Control, ﬂy in a great circle between

the two. Lines of longitude are simply special cases of great circles which pass through

the north and south poles, the angular distances between the poles being of course 180

◦

Lines of latitude are called small circles and represent different angular distances from

∗

Denotes biographical notes available in Appendix 3.

12.1 Introduction 297

Fig. 12.1. A portion of the surface of the Moon (south at top); above centre is the crater Tycho (from

which the bright rays radiate) and above this, and seen increasingly foreshortened, is the large crater

Clavius and smaller craters towards the edge. (Photographed at Mount Wilson Observatory, USA.)

the north and south poles. The largest small circle is the equator which is also a great

circle 90

◦

from the north and south poles.

The second step is to ﬁnd a method of representing this three-dimensional information

in two dimensions. One method is to project all the points on the surface of the sphere by

parallel lines on to a ﬂat disc called the plane of projection—in the same way as we see in

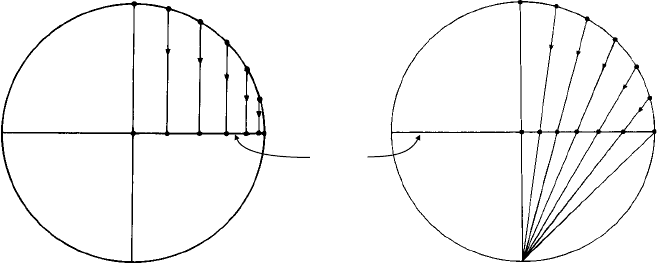
effect all the features on the surface of the Moon, Fig. 12.1. This has the disadvantage that

features near the edge of the Moon are seen foreshortened or ‘edge on’ and that craters,

which we know to be circular, are seen as elliptical in shape. The geometry is shown in

Fig. 12.2(a), the point of view being taken, in ‘Earth’ terms, from above the north pole.

Five points 15

◦

,30

◦

,45

◦

,60

◦

and 75

◦

from the north pole are shown and it is easily seen

how equal angles are represented by smaller distances as we move out from the centre.

However, in the stereographic projection we do not project the points on the surface of

the sphere in this way but rather project them to the south pole as shown in Fig. 12.2(b).

Now the distortion is, as it were, the other way round, equal angles are represented by

larger distances as we move out from the centre. However, the stereographic projection

has one very important geometrical advantage and that is that circles on the surface of the

sphere appear as circles, not ellipses, in the plane of projection. The geometry is shown

298 The stereographic projection and its uses

North

0°

15°

30°

45°

60°

75°

90°

Equatorial

plane

North

0°

15°

30°

45°

60°

75°

90°

South

(a) (b)

Fig. 12.2. A cross-section of the Earth perpendicular to the equator (the plane of projection) with the

north pole at the top and the south pole at the bottom, and points on the surface of the Earth at equal

angles 15

◦

,30

◦

,45

◦

,60

◦

,75

◦

and 90

◦

from the north pole. Viewed from a point a long distance above

(as we see the surface of the Moon) the points project on to the equatorial plane as shown in Fig. 12.2(a).

However, in the stereographic projection the points are projected to the south pole as in Fig. 12.2(b).

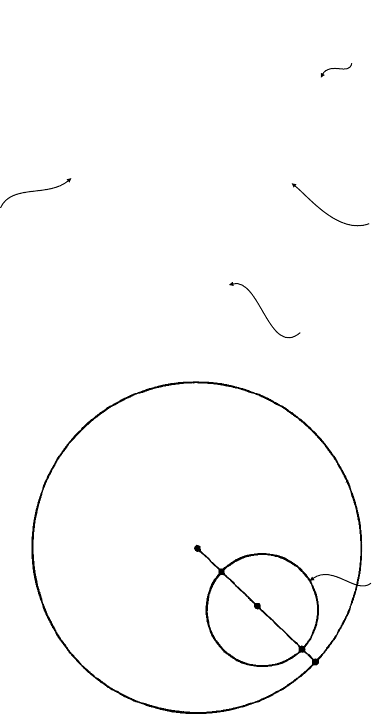
in Fig. 12.3(a). Here a circle in the northern hemisphere (a small circle) is centred about

O; all the points on this small circle are at equal angles from O (just as all the points on

a line of latitude are at equal angles from the north and south poles). All the points on

the circle are projected, as shown, to the south pole giving a cone—not a cone like an

ice-cream cone of circular cross-section but one of elliptical cross-section. However, in

any such elliptical cone there are two circular cross-sections inclined at equal angles to

the axis of the cone, one of which is the circle on the sphere and the other of which lies in

the plane of projection (the proof of this is left as Exercise 12.1). Figure 12.3(b) shows

a plan view of the equatorial plane, or the stereographic projection of the small circle.

Notice that O



, the projection of the centre of the circle is displaced towards the centre of

the projection and does not coincide with the point of a drawing-compass. This follows

from the fact, pointed out above, that in the projection equal angles are not represented

by equal distances.

Figures 12.2 and 12.3 show the construction for points in the northern hemisphere.

For points in the southern hemisphere we project instead to the north pole and represent

the intersections of the lines with the plane of projection by small unﬁlled circles instead

of dots.

Hence, in summary, and to return to our crystal, the stereographic projection consists

of an array of points and circles, called stereographic poles or simply poles representing

plane normals in the northern and southern hemispheres respectively and each labelled

with the appropriate Miller index of the crystal face they represent.

12.2 Construction of the stereographic projection of a cubic crystal 299

Small circle

on sphere

Small circle

in plane of

projection

Cone of elliptical

cross-section

Equatorial

plane of

projection

(a)

′

O′

Small circle

in plane of

projection

(b)

P′

Fig. 12.3. (a) The geometry of the stereographic projection of a small circle (or Moon-crater); all the

points on the circle are at equal angles to the centre O. The cone outlined by the lines of projection to

the south pole is elliptical in cross-section but its intersection with the equatorial plane of projection

is again a circle (see Exercise 12.1). P

and P

are two points on the small circle on the same line of

longitude (great circle through the north pole) which passes through the origin O. (b) The equatorial

plane, stereographic projection, or simply stereogram, of the small circle. Notice that the projected

points P



and P



are not equidistant from the projected centre of the small circle O



; this follows because

equal angles are not represented by equal distances (see Fig. 12.2(b)).

12.2 Construction of the stereographic projection of a

cubic crystal

Figure 12.4 shows a cubic crystal at the centre of the stereographic sphere with {100},

{110} and {111} faces and oriented for easy ‘Earth’ reference with the z-axis in the

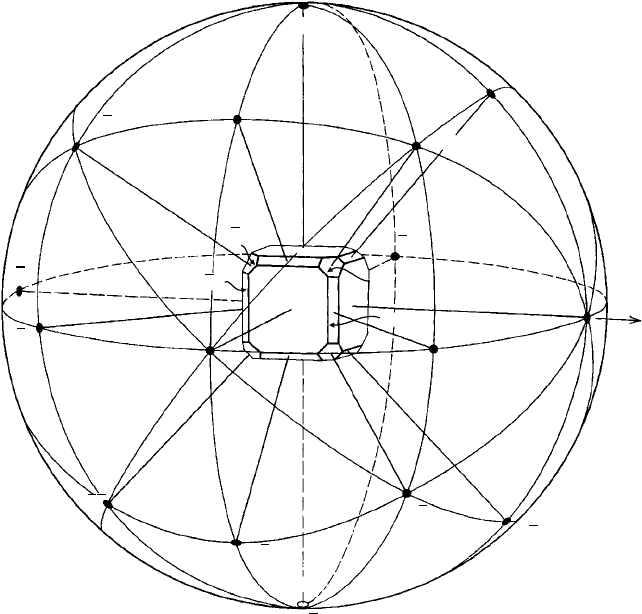
300 The stereographic projection and its uses

–

001

101

111

100

011

111

101

001

111

010

[010]

110

111

010

110

100

001

101

010

111

011

Fig. 12.4. A cubic crystal showing faces of the form {100}, {110} and {111} at the centre of the

stereographic sphere with face normals intersecting the surface of the sphere. Zones are shown as great

circles (diametral sections) on the sphere, the zone axis being normal to the diametral section. (From

Manual of Mineralogy, 21st edn, by C. Klein and C. S. Hurlbut Jr; John Wiley, 1993.)

direction of the north pole and the x and y axes in the equatorial plane (the stereographic

plane of projection). The normals to the crystal faces are shown and their intersections

with the sphere labelled with their {hkl}indices. The great circles on the sphere represent

zones. For example, planes or faces (00

1), (10

1), (100), (101) and (001) all lie in the

[010] zone and their normals lie on a great circle—a line of longitude which passes

through the north and south poles. Similarly, planes or faces (010), (111), (101), (1

11)

and (0

10) all lie in the [

101] zone and their normals all lie on a great circle in this case

inclined at 45

◦

to the north and south poles.

Figure 12.5 just shows the poles of planes in the equator and in the northern hemi-

sphere with the crystal and great circles omitted (to avoid the confusion of too many

12.2 Construction of the stereographic projection of a cubic crystal 301

100

101

110

111

001

110

111

010

011

100

111

101

100

010

011

001

Fig. 12.5. Poles of planes in the northern hemisphere (and in the equatorial plane of projection) and

the projection lines to the south pole, the intersections of which in the plane of projection are marked by

dots and their corresponding {hkl}indices indicate the position of the stereographic poles of the planes.

lines). The lines of projection to the south pole are shown and their intersections with the

stereographic plane of projection marked by dots with their corresponding {hkl} indices.

Finally, Fig. 12.6 is a ‘plan’ view of the stereographic projection showing the stereo-

graphic poles and again the great circles which project as the arcs of circles passing

through them. Now look back to Fig. 12.4. It is very important that you are able to

visualize the relationships between the faces in the crystal and their representation as

poles in the stereographic projection.

In plotting the exact positions of the poles in Fig. 12.6 it is important to remember

that equal angles are not represented by equal distances (except, of course, around the

perimeter). For example the (101) plane is 45

◦

between (001) and (100) but projects

at a smaller distance to (001) as shown in Fig. 12.2(b). Having plotted the positions of

the (101), (011), (0

11), etc. poles at their proper scale, the great circles through them

‘automatically’ give the positions of all the other poles or faces in the crystal—both

302 The stereographic projection and its uses

001

011

010

100

211

110

111

112

121

111

211

110

101

121

011

010

121

111

211

100

110

112

101

112

121

111

110

211

Fig. 12.6. A plan view of the stereographic plane of projection (the stereogram) showing the stereo-

graphic poles of the faces of the crystal in Fig. 12.4 and including both those faces ‘hidden from view’

in Fig. 12.4 and also additional faces (such as, for example, (112)) not drawn in Fig. 12.4. Great circles

on the sphere project as the arcs of circles in the plane of projection.

those ‘hidden from view’ such as (

111) and also ones not shown in the drawing of the

crystal in Fig. 12.4. For example (112) lies at the intersection of the zone through (101)

and (011) and also the zone through (111) and (001); i.e. by use of the addition rule

(Section 5.6.4) (101) +(011) = (112) and (111) + (001) = (112). Clearly, by drawing

more great circles and using the addition rule, planes of higher {hkl}values can be located

(Exercise 12.2).

Finally, we must now consider the points lying in the southern hemisphere where

the projection lines are made to the north pole and their intersections with the plane of

projection represented by small unﬁlled circles. These need not be shown as such in

Fig. 12.6 because clearly, for this orientation of the crystal (z-axis or (001) at the centre),

a plane such as (10

1) is coincident with (but ‘underneath’) the plane (101).

12.3 Manipulation of the stereographic projection:

use of the Wulff net

We now need a ‘stereographic graph paper’ in order to locate stereographic poles, zones

and zone axes. One such is the polar net (Fig. 12.7) which shows great circles like lines

12.3 Manipulation of the stereographic projection 303

Fig. 12.7. The polar net.

of longitude and small circles like lines of latitude. This net is not very useful. Instead

we use the net devised by G. V. Wulff

∗

(Fig. 12.8) which is, in effect, the polar net rotated

through 90

◦

; the great circles all pass through diametral points A...A in the plane of

the projection (‘top’ and ‘bottom’ of Fig. 12.8) and the small circles are at increasing

angles to these points, i.e. each small circle represents the loci of points at equal angles

to a point like 0 in Fig. 12.3 where 0 is now located in the plane of the projection. But

the Wulff net is rotatable (about a pin in the centre) and the diametral points A...Aor

axis of the net may be centered along the x-axis, or the y-axis (90

◦

rotation) or indeed

any direction in the plane of the projection.

The use of the Wulff net is best explained by way of some examples. Suppose we

wish to ﬁnd the angle between planes h

and h

(Fig. 12.9) (or, in Earth terms,

between New York and Bangkok). We rotate the Wulff net until h

and h

lie on

the same great circle as shown (full line) and the angle between them is simply ‘read

off’ from the divisions between the small circles which intersect at 90

◦

. The dashed

∗

Denotes biographical notes available in Appendix 3.