Hammond C. The Basics of Crystallography and Diffraction

Подождите немного. Документ загружается.

264 X-ray diffraction of polycrystalline materials

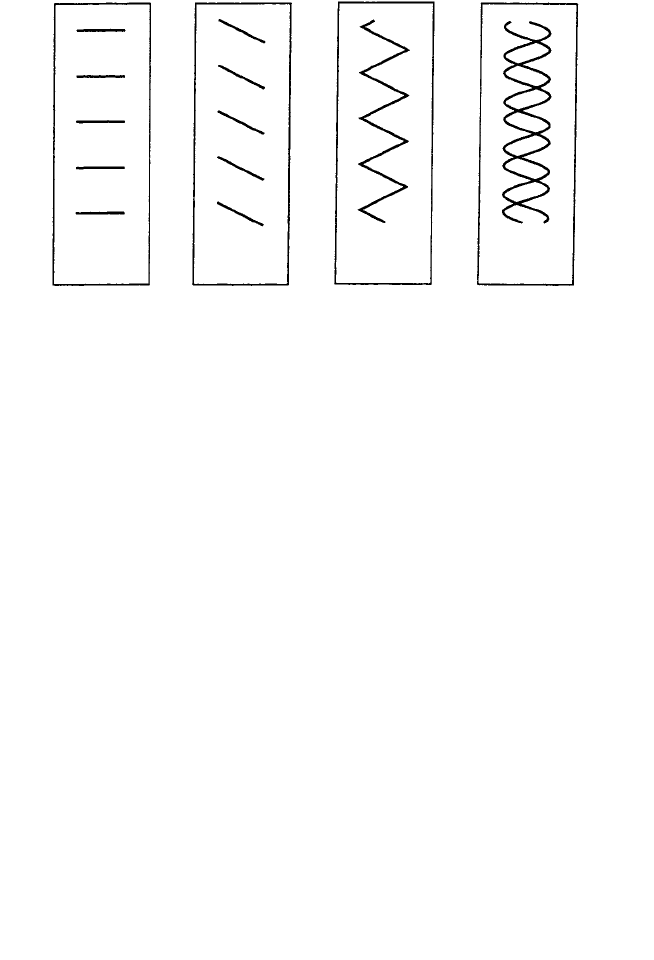
(a) (b) (c) (d)

Fig. 10.15. Representational models of the DNA structure. (a) Lines spaced the helical repeat distance

p and length 0.6 p; (b) lines inclined at (approximately) the same angle as one of the arms of the helices;

sine wave, in projection, of one of the helices; (d) two helices (represented as sine waves rather than

zig-zags) separated by a distance 3/8 p. (From A. A. Lucas et al. loc. cit.)

(a) (b) (c)

(d) (e)

Fig. 10.16. The optical transforms or diffraction patterns corresponding to the models shown in Fig

10.15(a)–(d) and Fig 10.14: (a) from horizontal lines spacing p and length 0.6p; (b) from lines inclined

as in one of the arms of the helices, the intensity maxima lie in a direction normal to the lines; (c) from

two sets of lines (zig-zags) representing the sine-wave projection of a single helix; (d) from two sine

waves separated by a distance 3/8 p; and (e) from the double-helix model as represented in Fig. 10.14.

(Photographs by courtesy of Prof. A. A. Lucas.)

10.5 X-ray diffraction of DNA: simulation by light diffraction 265

Next, we combine two zig-zags or two sine waves separated by the distance 3/8 p (Fig.

10.15(d)). The diffraction pattern is similar, but with the crucial difference that there are

gaps, or systematic absences, in the sequence of lines—the 4th (12th and 20th) lines

are missing (Fig. 10.16(d)). We can very easily understand this by drawing a diffraction

grating of slit separation p, working out the diffraction angles as in Section 7.4 and

then considering the contributions to the diffracted intensities of a second set of slits

separated by distance 3/8 p.Itisprecisely the same procedure that we used to determine

the diffracted amplitudes from a crystal with just two atoms per unit cell (Section 9.2

and Fig. 9.3(a)).

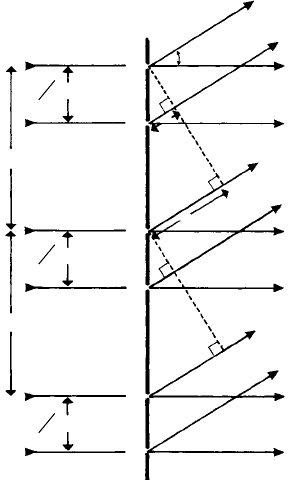
Figure 10.17(a) shows the geometry involved. Let f be the scattered amplitude from

each slit and consider ﬁrst the interference between the diffracted beams from the slits

A– – –A– – –. Maxima occur when the path difference x = nλ = p sin α

≈ pα

and the

amplitude per unit length p (or per unit cell) is f . Now consider slits B– – –B– – –. We

only need consider the contribution of one such slit (i.e. in one cell), since what applies

to one applies to all. The path difference between each A and B slit, y = 3/8x = 3/8nλ

and we can now construct the amplitude- or vector-phase diagrams for n = 0, 1, 2, 3,

4 … The results, and corresponding intensities in terms of f

are shown in Fig. 10.17(b).

The cyclic variations in intensities with zeros at n = 4, 12, 20, etc. are clear.

Figure 10.16(e) shows the diffraction pattern of the double helix with the phosphate

groups and planar bases shown as in Fig. 10.14. Its similarity to well-deﬁned X-ray

diffraction patterns of DNA is remarkable, especially so since it was arrived at by such

simple procedures.

(a)

Fig. 10.17. (continued)

266 X-ray diffraction of polycrystalline materials

Path diff,

Phase angle

Intensity,

(b)

135°

270°

405° (45 )°

540° (180 )°

675° (315 )°

1620° (180 )°

2700° (180 )°

135°

270°

45°

180°

0.586

3.414

Amplitude,

Fig. 10.17. (a) A diffraction grating of repeat distance p made up of two sets of slits A…A and

B…B…separated by distance 3/8 p. Maxima occur when the path difference x = nλ = p sin α

The amplitudes or intensities of the diffracted beams are modulated by interference between the waves

diffracted at each pair of slits A and B. (b) The vector-phase diagram for values of n = 0, 1, 2, 3, 4,

indicating zero intensity for n = 4 (and 12, 20, etc.).

However, there is a further problem to be solved. It was known (prior to 1952) that the

sugar-phosphate groups of nucleic acids were polar; the sequence of phosphate groups

along one direction is reversed in the opposite direction—in an analogous way as the

sequence of Zn and S atoms along a 111 (polar) direction in zincblende (Section 4.7).

How, therefore, are the two helices (Fig. 10.14) related; do the DNA backbones run

in the same, or in opposite directions? Francis Crick showed that they in fact ran in

opposite directions. The story is as follows

. As mentioned above, within living cells

the DNA is surrounded by the high water content of the cell as in a B-DNA ﬁbre.

Again, I am indebted to Professor Amand Lucas on whose paper, A-DNA and B-DNA: Comparing their

Historical X-ray Fibre Diffraction Images, Journal of Chemical Education 85, 737 (2008) I have largely based

this brief account. Professor Lucas and his colleagues have also prepared (available on request) two slides;

one consisting of nine optical masks for B-DNA and the other twelve optical masks consisting of the same

nine masks for B-DNAplus two additional masks for A-DNA and one mask to disprove the co-oriented model

of double-stranded DNA. The use of these masks, in demonstrating the relations between the structures and

diffraction patterns of DNA, is explained in the paper.

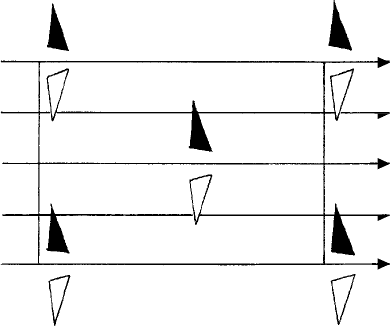
10.6 The Rietveld method for structure reﬁnement 267













Fig. 10.18. A portion of a pattern based on space group C2. An (open) triangle at height + is turned

over by the operation of a horizontal diad axis (double-headed arrows along the y-axis) to one at height—

(black triangle). The pair of triangles is repeated by the C-face-centring lattice point. Screw diad axes

(single-headed arrows) arise between the diad axes.

However, when the water content of the ﬁbre is reduced, the strands shrink slightly,

but more importantly, they pack together in nearly, but not quite, an hexagonal array

(A-DNA). In order to achieve the most efﬁcient packing, the helical ‘grooves’ of one

strand locate into the ‘projections’ of the next—in just the same way that a bundle of

ordinary screws (or threaded rods) pack together; the ‘tops’ of the threads of one screw

ﬁtting in to the ‘bottoms’ of the threads of the next. This results (in the case of A-DNA)

in a C-face centred monoclinic, rather than an hexagonal unit cell. Gosling and Franklin

determined the space group to be C2 (a ‘permissible’ space group—see Table 4.1): the

only symmetry elements which the unit cell possesses are the diad (and screw diad) axes

running perpendicular to the strands. Crick realized that, since the cell possessed diad

symmetry, the DNA molecules must also possess diad symmetry and that the only way

this could be achieved was for the polar backbones to run in opposite directions. This

is readily seen in Fig. 10.18, the black and white triangles, related by diad symmetry,

representing the opposite, or counter-oriented molecular chains. This deduction, arrived

at by such simple crystallographic reasoning, was of crucial importance in guiding

Watson and Crick in their model building of the structure of DNA.

10.6 The Rietveld method for structure reﬁnement

Powder diffraction data has long been used to identify and characterize crystalline mate-

rials, particularly through the use and development of the X-ray Powder Diffraction

File (Section 10.3.2). However, until the advent of the Rietveld method it was little

used for the determination of all but the simplest of crystal structures largely on account

of overlapping peaks and the consequent difﬁculty of accurately measuring integrated

268 X-ray diffraction of polycrystalline materials

intensities, this being the ﬁrst step in determining the structure factors of the reﬂections

which can be then used, as in single-crystal data, to solve or reﬁne structures. This peak

proﬁle ﬁtting procedure clearly only works for relatively simple structures which yield

diffraction patterns with minimal peak overlap. One may say that the ﬁrst such peak

proﬁle-ﬁtting procedure was carried out (albeit with single crystals) by W. L. Bragg in

1913 who established, from relative peak intensities, the location of the S atoms in FeS

(Section 4.7, Fig. 4.16).

The Rietveldmethod, incontrast, doesnotmeasure, norattempt to measure, integrated

intensities as such but records the whole powder diffraction pattern: the measurement

of intensity at each 2θ step constitutes a data point and the whole set of such data

points is compared with those calculated. The calculation takes into account not only

structural parameters (unit cell size, atom positions and occupancy factors) but also

scale factors, background intensity coefﬁcients and proﬁle parameters describing peak

shapes and widths. These parameters are then varied in a least-squares procedure until

the calculated pattern best matches the observed pattern. The quantity R to be minimized

is given by:

R =



(

− Y

)

where Y

is the observed intensity at step i, Y

is the calculated intensity and w

is a

weighting assigned to each step—the stronger the observed intensity (i.e. the smaller the

counting error), the larger is w

Such is the process of Rietveld reﬁnement, but in order for it to be successful a

large number of conditions, both theoretical and experimental, need to be met. First

the ‘input’ structure (unit cell dimensions, atom positions, occupancy of atomic sites,

etc.) needs to be a close approximation of that which is ultimately to be determined

by the reﬁnement—how close depends of course on the complexity of the structure.

Then, as mentioned above, account must be taken of all the other factors which affect

the observed intensities: ﬂuorescence from the specimen, detector noise, thermal diffuse

and incoherent scattering, scattering from the sample holder, beam collimator and slits

and preferred orientation (Section 10.4). The Rietveld method is able to accommodate

moderate amounts of preferred orientation, which may otherwise be difﬁcult or impossi-

ble to eliminate (see point 3 below), by the inclusion of reﬁning parameters which model

the effect. In so doing preferred orientation may both be quantiﬁed and also removed as

a confounding inﬂuence on the other variables.

The experimental conditions are no less demanding. They may be summarized as

follows:

(1) Accurate alignment of diffractometer (to ensure accurate 2θ values).

(2) Correct positioning of specimen (both in the diffractometer and Debye–Scherrer

arrangement).

(3) Correct choice of Soller slits (which limit lateral beam divergence in the diffrac-

tometer) to avoid low-angle peak ‘tails’ in low-2θ reﬂections.

10.6 The Rietveld method for structure reﬁnement 269

(4) Elimination (as far as possible) of preferred orientation effects; even the process of

pressing a powder into a holder, or introducing it into a capillary tube, can give rise

to preferred orientation.

(5) Constant volume condition. In the Debye–Scherrer arrangement this is achieved

automatically (except in the case of strongly-absorbing specimens). In the diffrac-

tometer it is achieved if the incident beam remains within the area of the specimen

(a potential problem at low 2θ angles) and if the beam does not penetrate to the

underlying holder (i.e. is regarded as ‘inﬁnitely thick’). The constant volume con-

dition arises because the area of specimen irradiated varies as 1/ sin θ and the depth

of operation varies as sin θ, hence the volume is independent of θ. Some diffrac-

tometers incorporate divergence slits which open out as 2θ increases—resulting in

a gain in intensity, and hence reduced counting errors, at high 2θ angles but also an

increase in irradiated volume which must be accounted for.

(6) Apowder particle size of ∼1–5 μm; for sizes smaller than this line broadening needs

to be taken into account and for sizes much larger than all crystallite orientations

may not contribute equally to the intensity, a problem akin to preferred orientation.

All these considerations indicate the complexity of the computer programs required

in a Rietveld reﬁnement.

The technique was invented, and the ﬁrst programs written, by Hugo M. Rietveld

to reﬁne structures recorded by neutron, rather than X-ray, diffraction. He records that

when he ﬁrst announced the techniques at the Seventh Congress of the IUCr in Moscow

in 1966, ‘the response was slight, or rather non existent’.

Since then it has become a

major tool in structure determination, particularly since increasing computer power has

led to its application in X-ray diffraction (where line proﬁles are more complex than those

in neutron diffraction). Apart from being able to solve the structures of intrinsically-ﬁne

crystalline materials it has found particular application in, e.g., perovskites and super-

conductors in which the various structural forms arise from displacive transformations

(see Section 1.11). It is also able to deal with multiphase specimens and to detect the

presence of amorphous components.

The ﬁnal word must come from Rietveld himself ‘… the method is not to be treated as

a black box. One must be continually aware of the limitations, not only of this method,

but in general of all least squares methods.’

Exercises

10.1 Show, by simple geometrical reasoning, that in the X-ray monochromator (Fig. 10.2) the

curved reﬂecting crystal planes should have a radius twice that of the focusing circle.

10.2 Show, by simple geometrical reasoning, that in the back-reﬂection X-ray powder photo-

graph (Fig. 10.5), the reﬂections are most sharply focused when R

= xy where R = the

radius of the ring, x = the specimen–ﬁlm distance and y = the distance of the (effective)

source S behind the ﬁlm.

H.M. Rietveld, ‘The early days, a retrospective view,’ in The Rietveld Method p. 39–42, ed. R.A. Young.

IUCr/Oxford Science Publications, Oxford University Press, Oxford (1993).

270 X-ray diffraction of polycrystalline materials

10.3 Determine the d-spacings of the strongest low-angle reﬂections in the Debye–Scherrer ﬁlm

of quartz (Fig. 10.7) and check that they correspond (within the limits of experimental

accuracy) with those indicated in Fig. 10.4 or listed in Fig. 10.8.

(Hint: the precise locations at which 2θ = 0 and 180

◦

are not found from the centres of

the holes in the ﬁlm (which might be slightly displaced) but by determining the mid-points

of the low-angle and high-angle reﬂections, respectively. The distance between these mid-

points corresponds to an angle of 180

◦

and the linear scale can be related to the angular

scale and the 2θ values. Hence the d-spacings of the reﬂections can be found using Bragg’s

law. (The ﬁlm is taken using ﬁltered CuKα radiation which includes both the Kα

and Kα

components. At low angles these are unresolved, λCuK ¯α = 1.542 Å, but at high angles

they are resolved, λCuKα

= 1.541 Å, λCuKα

= 1.544 Å.)

10.4 Crystalline polypropene may be assigned a monoclinic unit cell with lattice parameters

a = 6.65 Å, b = 20.96 Å, c = 6.50 Å and β = 99.3

◦

(see Section 4.8.2). The polymer

chains are orientated along the c-axis. The table shows the d spacings, relative intensities

and corresponding hk0, hkl and hk2 indices (data from Natta, G., Corradini, P. and Cesari,

M. (1956), Rend. Acad. Naz. Lincei 21, 365).

d/Å(hk0) Intensity

†

d/Å(hk1) Intensity

†

d/Å(hk2) Intensity

†

6.21 110 s 4.14 111 m 3.06 022 mf

5.20 040 vs 4.06 131 s 3.05 112 mf

4.74 130 s 4.03 041 s 2.50 202 f

3.50 150 m 2.11 202 mf

3.46 060 m

3.25 200 mf

3.11 220 mf

†

Intensities: s = strong, v = very, m = medium, f = faint.

2degrees

44.0 44.5 45.0 45.5 46.0 64.0 64.5 65.0 65.5 66.0 81.5 82.0 82.5 83.0 83.5 84.0

Intensity (arbitrary units)

(a)

(b)

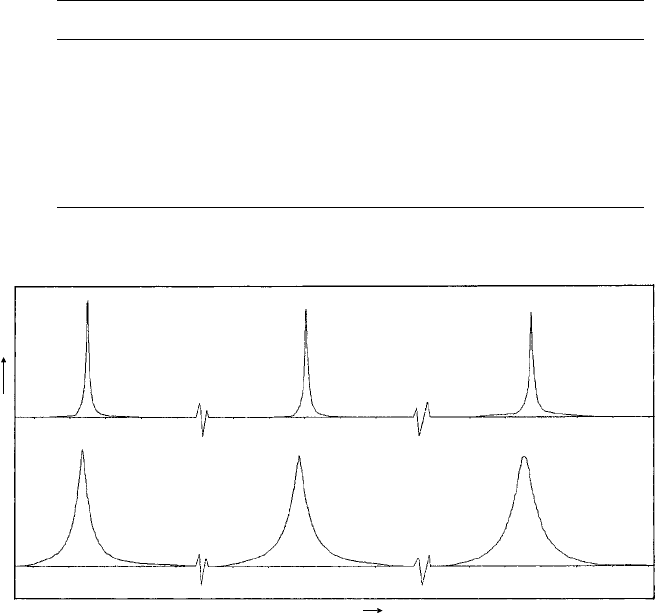
Fig. 10.19. Diffractometer charts (CuKα

radiation, λ = 1.541 Å) showing the ﬁrst three reﬂections

for a steel specimen (α-Fe, bcc) in (a) the annealed condition and (b) after heavy surface abrasion giving

broadened and shifted X-ray diffraction peaks which arise from residual stresses on the micro- and

macroscale and a reduction in crystallite size. (Data by courtesy of Mr D. G. Wright.)

Exercises 271

Given that the X-ray photographs in Fig. 10.11 were taken with CuKα radiation (λ =

1.542 Å) and that the specimen-ﬁlm distance (corrected for printing = 36 mm), index the

reﬂections and show that in Fig. 10.11(b) the polymer chains are orientated along the

tensile axis.

10.5 With reference to Fig. 10.19, determine β (expressed in radians) for each of the peaks from

the half-height peak widths of the annealed (β

Inst

) and abraded (β

OBS

) specimens. On

rtibra(ytisnetnI)stinuyra

(1010)

(1011)

(0002)

6.00

×10

6.00

5.40

5.80

4.20

3.60

3.00

2.40

1.80

1.20

0.60

34.0 36.0 38.0 40.0 42.0 44.0

×10

5.40

4.80

4.20

3.60

3.00

2.40

1.80

1.20

0.60

34.0 36.0 38.0 40.0 42.0 44.0

(a)

rtibra(ytisnetnI)stinuyra

(1010)

(1011)

(0002)

(110)

(b)

degrees 2

Fig. 10.20. Diffractometer charts (CuKα

radiation, λ = 1.541 Å) showing the ﬁrst three reﬂections

for a titanium alloy (Ti-6% Al-4% V) powder specimen in (a) the mechanically milled condition and (b)

following consolidation and heat treatment which gives rise to an increase in grain size and precipitation

of the β phase (bcc) in the α phase (hexagonal) alloy matrix. (Data by courtesy of Mr D. G. Wright and

Dr A. Brown.)

272 X-ray diffraction of polycrystalline materials

the assumption that the broadening arises solely from microstrain, determine the micros-

train and hence residual stress given the Young modulus for iron E = 207 GPa (see

Section 10.3.4).

10.6 With reference to Fig. 10.20, electron microscopy indicates that the grain size of the milled

powder (a) is in the range 10–50 nm and that of the consolidated powder (b) is 5 μm and

above. On the basis that the increased broadening in (a) arises solely as a result of the ﬁne

crystallite size, show that the X-ray data is consistent with the microscopical data.

Electron diffraction and its

applications

11.1 Introduction

In Section 7.3 we discussed the wave- and particle-like characters of light which are

linked by Planck’s equation E = hc/λ; and also the wave-like character of moving

particles which is linked to their mass and velocity by de Broglie’s equation λ = h/mv.

The common or ‘linking factor’ in both equations being Planck’s constant h = 6.63 ×

−34

Js. In the caseof neutrons (Section9.7 and Exercise9.3), itisthe thermalconditions

in the reactor which give rise to the neutron velocities, and hence mv values which, when

substituted in de Broglie’s equation, give wavelengths very similar to those for X-rays

(Section 9.7). In the case of electrons in the transmission electron microscope the velocity

and hence momentum mv of the electrons (m being relativistically corrected) depends on

the accelerating voltage V and is determined by equating the potential energy eV (lost)

where e is the charge on the electron with the kinetic energy

(gained). The resulting

λ values are very small (see Exercise 11.l), for example in a microscope operating at

300 kV, λ = 1.97 pm (0.0197 Å) and this of course is the basis of the high resolving

power (or small limit of resolution) of the electron microscope in comparison with

the light microscope as described in Section 7.5. Finally, it should be emphasized that

de Broglie’s equation applies to all moving particles, not just neutrons and electrons—

including pieces of chalk thrown at inattentive students in lectures! However, as a simple

calculation shows, the associated wavelengths are very small.

Whereas X-rays are scattered by the electrons in atoms, the incident electrons are

primarily scattered by the protons in the nuclei, the scattering amplitude being propor-

tional to Z. The electrons do, however, play a role insofar as they ‘shield’ the nuclei

from the incident electrons by an amount proportional to f , the X-ray atomic scattering

factor. Hence, the electron atomic scattering amplitude, f

is proportional to (Z −f ). It is

normally expressed as a scattering length (rather than a number like f ) and the electron

scattering intensities are thus expressed as areas or atomic scattering cross-sections.

The important consequence is that on average f

∝

√

Z (rather than f ∝ Z for

X-rays) so that light elements scatter more strongly, in comparison to heavy elements,

than X-rays. More important still the amount of scattering is much greater than for X-rays

by a factor of l0

or l0

such that electron beams are attenuated much more rapidly. Hence

in electron diffraction the dynamical interactions discussed in Section 9.l are much more

important than in X-ray diffraction and must always be taken into account in any attempt

to relate observed electron beam intensities to atomic positions. There is, in electron