Hammond C. The Basics of Crystallography and Diffraction

Подождите немного. Документ загружается.

244 X-ray diffraction of polycrystalline materials

However, in situations in which the crystals are not randomly orientated the diffracted

intensity in the cones will not be uniform and in order to determine the extent of the ‘non-

randomness’ the whole, or a large part, of the cones needs to be recorded. In metallurgy

and materials science the ‘non-randomness’ of crystals is known as texture or preferred

orientation whereas in earth science it is known as fabric or petrofabric. (The word

texture in earth science has quite a different meaning and refers rather generally to grain

shapes and grain size distributions—a different nomenclature which is a possible source

of confusion.)

The analysis of preferred orientation (texture or fabric) is important since it

almost invariably arises as a consequence of the processes of crystallization and

re-crystallization, sintering, extrusion and hot deformation which occur either in the

short time-scale in materials processing or in the long time-scale in the earth’s crust

and mantle. The simplest experimental techniques are the ‘ﬁbre’ X-ray techniques in

which the crystals are orientated with a particular crystallographic direction (or direc-

tions) along the ﬁbre axis. In the case of rolled/recrystallized metal sheets or strata in the

earth’s crust the analysis is more complicated—in addition to preferred orientation along

some reference (e.g. rolling or shear) direction there may also be preferred orientation of

the crystals with respect to the plane of the metal sheet or rock strata. Such textures may

be represented by stereographic projections referred to as pole ﬁgures, fabric or petro-

fabric diagrams (Section 10.4) or, more quantitatively, by what are known as orientation

distribution functions.

Fibre techniques play an essential experimental part in the determination of the struc-

tures of long-chain organic molecules in which the aim is to draw out a ﬁbre from a

solution which contains a sufﬁcient number of molecules, all perfectly aligned along the

ﬁbre axis, and which give rise to reﬂections of measurable intensity. A simple descrip-

tion of the structure of DNA, which was discovered by such a technique, is given in

Section 10.5.

Finally, X-ray (and neutron)powder diffractiontechniques arebeing used increasingly

in crystal structure determination, once the sole preserve of single crystal techniques.

This has arisen from the necessity of determining the structures of the many materials of

technological importance—e.g. clay minerals, ferrihydrites, etc.—which are ﬁnely crys-

talline and/or poorly ordered and which cannot be grown into crystals of large enough

size (∼0.2 mm) to be investigated by single crystal techniques. However, powder tech-

niques are only able to deal with situations in which the structure (depending on its

complexity) is known approximately and are thus better described as structure reﬁne-

ment techniques. The principal of these—known as the Rietveld method—is outlined in

Section 10.6.

10.2 The geometrical basis of polycrystalline (powder) X-ray

diffraction techniques

We begin, perhaps rather surprisingly, with a theorem which we learned off-by-heart

(or should have done) in our early geometry lessons at school—never imagining that

it would ever come in useful! The theorem comes from The Elements of Euclid, the

mathematics textbook which has remained in print ever since it was ﬁrst written in

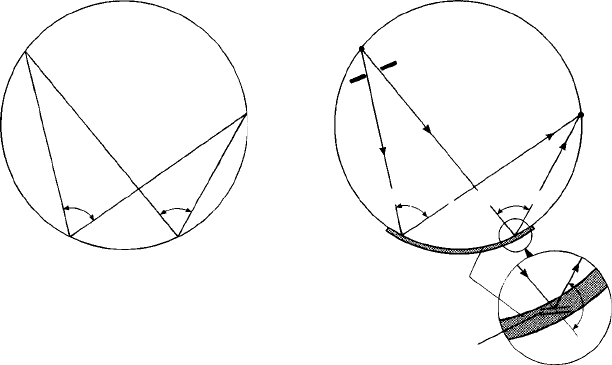
10.2 X-ray diffraction 245

Source

Divergence slit

Focused

reflection

(inset)

Reflecting planes

Polycrystalline

specimen

(a) (b)

(180°–2u)

Fig. 10.1. (a) The geometrical basis of X-ray powder diffraction techniques; for two given points S

and D on the circle, the angle x at the circumference is constant, irrespective of the position of P. (b)

Application to an X-ray focusing camera. S is a source of monochromatic X-rays, the angular spread of

which is collimated by a divergence slit to strike a thin layer of a powder specimen on the circumference

at P…P. Angle x = (180

◦

− 2θ), hence any crystal planes in the right orientation for Bragg’s law to be

satisﬁed reﬂect to give a focused beam (as shown in the inset for a particular d

hkl

-spacing). Note that the

reﬂecting planes are not in general tangential to the circumference of the camera, although in practice

they are closely so.

c. 300 B.C. The theorem, which is proved in Proposition 21, Book III of The Elements,

states that ‘the angles in the same segment of a circle are equal to one another’. It follows

the other equally well known theorem (Proposition 20) that ‘the angle at the centre of a

circle is double that of the angle at the circumference on the same base, that is, on the

same arc’.

The former theorem is illustrated (without Euclid’s proof) in Fig. 10.1(a) and may

be simply restated by saying that for any two points S and D on the circumference of a

circle, the angle shown as x is constant irrespective of the position of point P. Now let

us make use of this geometry in devising an X-ray camera (Fig. 10.1 (b)). Let S be a

point or slit source of monochromatic X-rays (the slit being perpendicular to the plane

of the paper) and let part of the circumference P… P be ‘coated’ with a thin ﬁlm of a

polycrystalline specimen.

The X-rays diverge from the source S and in order that they should only strike the

specimen we limit or collimate them with a (divergence) slit as shown. Now the angle

x is, in terms of Bragg’s law, the angle (180

◦

–2θ)—and whenever this is the cor-

rect Bragg angle for reﬂection for a particular set of hkl planes, reﬂections occur from

all those crystals in the specimen which are in the right orientation and the reﬂected

beams, as proved by Euclid, all converge to point D. In short D is a point where all the

reﬂected beams for a particular d

hkl

spacing are focused. Different positions of D on the

246 X-ray diffraction of polycrystalline materials

circumference correspond to different x, hence different (180

◦

–2θ) values. Hence we

will have a series of focused diffraction lines, one for each d

hkl

-spacing in the specimen,

around the circumference of the circle.

The Bragg reﬂecting geometry is shown in detailinthe little ‘inset’diagram below Fig.

10.1(b) which shows the orientation of the reﬂecting planes in one part of the specimen

and the angle 2θ between the direct and reﬂected beams. Notice that the reﬂecting planes

are not (except for some particular part of the specimen) tangential to the circumference.

A ﬁlm placed around the rest of the circumference of the circle will record all the

reﬂected beams and this arrangement is the basis of the Seeman–Bohlin camera and the

variants of it devised by Guinier and Hägg. They are called focusing X-ray methods

because they exploit the focusing geometry of Euclid’s circle which is thus called the

focusing circle.

The focusing geometry can also be used to provide a monochromatic source of X-rays

(Fig. 10.2). The source S is now the line focus of an X-ray tube from which a spectrum of

X-ray wavelengths (the ‘white’radiation with superimposed characteristic wavelengths,

Kα

,Kα

,Kβ etc.) is emitted. A single plate-shaped crystal is cut such that a set of

strongly reﬂecting planes is parallel to the surface. The crystal iscurved or bent to a radius

of curvature twice that of the focusing circle and then (ideally) is shaped or ‘hollowed

out’ such that its inner surface lies along that of the focusing circle. The position of the

source S, and hence the angle (180

◦

–2θ) is, together with the d

hkl

spacing of the crystal

planes, chosen to reﬂect, say, only the strong Kα

component of the whole X-ray spec-

trum which is focused to a point or line D, symmetrical with the source S. D becomes, in

Polychromatic

source

of X-rays

Divergence slit

(180°–2u) (180°– 2u)

Focused

monochromatic

(Ka

)X-ray

beam

Curved and shaped crystal,

the reflecting planes are at

angle u to the incident and

diffracted beams

Fig. 10.2. The principle of the X-ray monochromator. The crystal planes are curved to a radius twice

that of the focusing circle such that they make the same angle (θ ) to the divergent incident beam. The

surface of the crystal is also shaped so as to lie precisely on the focusing circle. The source and focus

of the reﬂected beams are symmetrical (i.e. equal distances) with respect to the crystal and θ and the

hkl

-spacing of the crystal planes are chosen such that only the strong Kα

X-ray wavelength component

is reﬂected.

10.2 X-ray diffraction 247

effect, the line source of a beam of monochromatic X-rays, which can be used ‘upstream’

of the Seeman–Bohlin camera as the source S of monochromatic X-rays.

The symmetrical arrangement is also made use of in the X-ray diffractometer, which

has become by far the most important classical X-ray powder diffraction technique. The

diffractometer has become, in effect, the X-ray data acquisition end of a computer in

which the data can be stored, analysed, plotted, compared with standard powder data

ﬁles, etc. The advantages are enormous; the disadvantage, if it can be called such, is

that students may simply regard the diffractometer as a ‘black box’ to generate data,

without understanding the principles on which the instrument works, nor the parameters

underlying the data analysis procedures.

The symmetricalor Bragg–Brentano focusinggeometry of thediffractometer isshown

in Figs 10.3(a) and (b). As described in Section 9.6, the source of monochromatic

X-rays, S (from a monochromator upstream of the diffractometer) is at an equal distance

Arc centred on specimen

Flat specimen: centre

lies within the focusing

circle

Focusing circle

Focusing circles

(a) (b)

(c)

Fig. 10.3. The principle of the X-ray diffractometer. The source–specimen and specimen–detector

slit distances are ﬁxed and equal, (a) The situation for a small θ angle and (b) for a large θ angle, the

source and detector moving round the arc of a circle centred on the specimen. Notice the change in the

diameter of the focusing circle and the fact that, since the specimen is ﬂat, complete focusing conditions

are not achieved (dashed line in (a)), (c) An asymmetrical specimen arrangement for the same 2θ angle

as in (b), the position and diameter of the focusing circle have changed such that the detector slit is no

longer coincident with it. The reﬂecting planes are now those which make (approximately) angle α to

the specimen surface (see Fig. 9.20).

248 X-ray diffraction of polycrystalline materials

and equal angle to the specimen surface as D, the ‘receiving slit’ of the detector (a

proportional counter). The 2θ angle is continuously varied by the source and detector

slit tracking round the arc of a circle centred on (and therefore at a ﬁxed distance from)

the specimen. Figure 10.3(a) shows the situation at a low θ angle and Fig. 10.3(b) shows

the situation at a high θ angle. In some instruments the specimen is ﬁxed and the source

and detector slit rotate in opposite senses; in others the source is ﬁxed and the specimen

and detector slit rotate in the same sense, the detector slit at twice the angular velocity

of the specimen—but the result geometrically is the same.

However, the important point to note is that the polycrystalline specimen as used in

a diffractometer is ﬂat, and not curved to ﬁt the circumference of the focusing circle.

Focusing therefore is not perfect—the reﬂected beams from across the whole surface of

the specimen do not all converge to the same point: those from the centre converge to a

point a little above those from the edges, as shown in Fig. 10.3(a). The diffractometer is

hence called a semi-focusing X-ray method. In practice the deviation from full focusing

geometry is onlyimportant (in the symmetrical arrangement) atlowθ anglesand in which

a large width of specimen contributes to the reﬂected beam. It is not however laziness or

experimental difﬁculty which prevents specimens being made to ﬁt the circumference of

the focusing circle, but the fact that, unlike the situation for the Seeman–Bohlin camera,

the radius of the focusing circle changes with angle as is shown by a comparison with

Figs 10.3(a) and (b).

As pointed out above, in the symmetrical arrangement, in which the specimen surface

makes equal angles to the incident and reﬂected beams, the only crystal planes which

contribute to the reﬂections are those which lie (approximately) parallel to the specimen

surface, particularly when the divergence angle of the incident beam, and therefore the

irradiated surface of the specimen, is small. In situations in which the d

hkl

spacings

of planes which lie at large angles to the specimen surface need to be measured (e.g.

in determining the variation of lattice strains from planes in different orientations), the

specimen is rotated as shown in Fig. 10.3(c); the angle of rotation α is of course (approx-

imately) equal to the angle of the reﬂecting planes to the specimen surface (Fig. 9.20).

In doing so, however, the symmetrical Bragg–Brentano focusing geometry is lost; the

focusing circle changes both in diameter and position, as shown in Fig. 10.3(c), and

the detector slit is no longer at the approximate line of focus, but in this case beyond

it where the beam diverges and broadens. This deviation from the focusing geometry

may be serious because the observed ‘broadening’ at the detector slit could be misinter-

preted as arising from a variation in reﬂection angle as a result of a variation in lattice

strain. The problem may be partially overcome in two ways. First, the detector slit may

be moved along a sliding-arm arrangement so as to coincide more precisely with the

line of focus. However, this may itself introduce errors in the angular measurements

because of the difﬁculty of achieving a precise radial alignment of the slider. Second,

the angular divergence of the incident beam may be restricted to very low values—say

0.25

◦

–0.5

◦

—such that the broadening of the beam at the detector slit is very small, and

this is now the preferred option.

An example of an X-ray diffractometer chart or ‘trace’ for quartz (SiO

) is given in

Fig. 10.4. The d

hkl

-spacings and relative intensities of the reﬂections may be used to

identify the material, as described in Section 10.3 below.

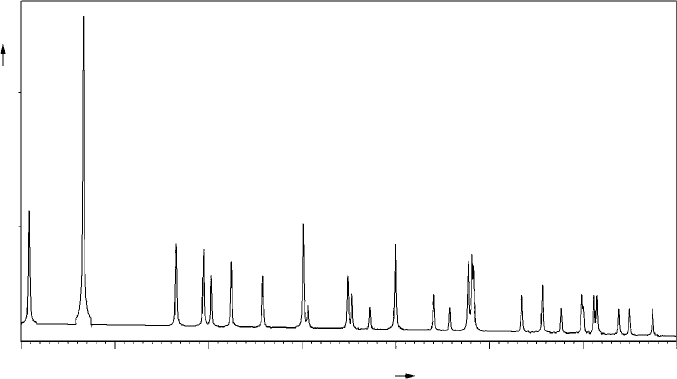
10.2 X-ray diffraction 249

Square root of intensity (arbitary scale)

4.257[Å]

2.457[Å]

3.342[Å]

2.282[Å]

1.818[Å]

1.542[Å]

1.382[Å]

1.372[Å]

40 50 60 70 80 90

Diffraction Angle [°2u]

Fig. 10.4. An example of an X-ray diffractometer chart of intensity of the reﬂected beams (ordinate) vs

2θ angle (abscissa). The intensity scale is non-linear (square root) to emphasize the weaker reﬂections.

The specimen is polycrystalline SiO

(quartz), CuKα

, radiation (λ = 1.541 Å). The d-spacings (Å) of

the reﬂections are indicated (compare with Figs 10.7 and 10.8). (Courtesy of Mr. D. G. Wright.).

There are two other ‘classical’ X-ray powder techniques of interest—the back reﬂec-

tion method in which the whole or part of the diffraction cones are recorded on ﬂat ﬁlm

(an experimental arrangement identical to that for the Laue back reﬂection method) and

the Debye–Scherrer technique in which a thin rod-shaped specimen or a powder in a

capillary tube is set at the centre of a cylindrical camera.

The geometry of the back reﬂection powder method is shown in Fig. 10.5. The

effective position of the source S is determined by the design of the collimator tube

which passes through a hole in the centre of the ﬁlm. In practice the divergence angle is

very small, of the order 0.5

◦

–2

◦

. Notice that, like the diffractometer, it is a semi-focusing

method—all the reﬂected beams from the (ﬂat) specimen surface focus approximately at

the circumference of the focusing circle. However, the ﬂat ﬁlm can be placed only at one

distance x from the specimen: if x is the focal distance of the high 2θ angle reﬂections

as shown, it will not be at the focal distance of the lower 2θ angle reﬂections. In practice

a ‘compromise’ value of x is chosen such that the diffraction rings of particular interest

are most sharply focused.

The great advantage of the Debye–Scherrer method over the diffractometer (and to a

lesser extent the Seeman–Bohlin method and its variants) is that only very small amounts

of material are required for, say, insertion into a capillary tube.

The geometry and specimen–ﬁlm arrangement in the Debye–Scherrer camera are

shown in Fig. 10.6. The cylindrical specimen (a powder in a capillary tube or a cemented

powder in the form of a little rod) is placed at the centre of a cylindrical camera. The strip

of ﬁlm may be ﬁtted round the circumference of the camera in several ways: it may have

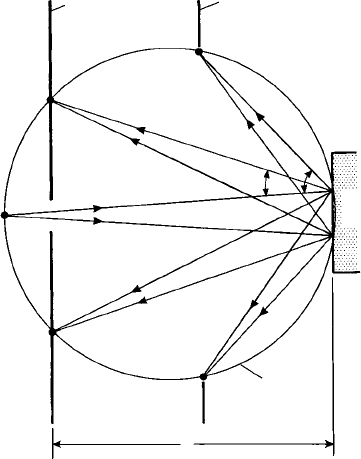
250 X-ray diffraction of polycrystalline materials

Film position for

focused higher

angle reflections

Source

Polycrystalline

specimen

Focusing

circle

Film position for

focused lower

angle reflections

Fig. 10.5. The geometry of the back reﬂection X-ray powder method; the diverging X-ray beam from

an (effective) source S passes through a hole at the centre of the ﬁlm. The reﬂected beams for two

reﬂections are shown. The ﬁlm is shown placed at a specimen–ﬁlm distance x so as to intercept the

higher angle reﬂectionssuch that theyare sharply focused. Inorder to interceptthe lower anglereﬂections

such that they are sharply focused it would need to be moved closer to the specimen as indicated. In

practice a ‘compromise’ value for x is chosen which is acceptable since the divergence angle, and the

de-focusing of the incident beam, is small.

a single hole punched at its centre and so arranged to coincide with the ‘exit’ direction

of the X-ray beam (the ends of the ﬁlm being each side of the ‘entrance’ direction of the

X-ray beam) or vice versa. However, the usual way is to punch two holes in the ﬁlm, one

to match the ‘entrance’ and the other to match the ‘exit’ directions of the X-ray beam,

the two ends of the ﬁlm now being at the ‘top’ or ‘bottom’ of the camera as shown. This

‘asymmetrical’ arrangement or ‘setting’ has the advantage that a complete range of 2θ

angles—from 0

◦

to 180

◦

—may be recorded on one side of the ﬁlm without a ‘cut-off

occasioned by the presence of a ﬁlm end. In this way accurate d

hkl

-spacings may be

determined and any effects of ﬁlm shrinkage accounted for.

The position of the effective source S is determined by the design of the collimator.

The focusing circle for a particular reﬂection is shown; however, this only represents the

physical situation very approximately since the reﬂected beams arise to different extents

from the whole volume of the specimen and the position of the source S and the focusing

effect is by no means as precise as that drawn in Fig. 10.6.

An example of a Debye–Scherrer ﬁlm (asymmetrical setting) is shown in Fig. 10.7.

The 2θ = 0

◦

and 2θ = 180

◦

positions can be worked out exactly by determining

10.2 X-ray diffraction 251

Focusing circle for

one reflected beam

Film ends

Exit hole

in film

Camera

circumference

X-ray

source

Entrance

hole in film

(a)

(b)

Fig. 10.6. (a) The geometry of the Debye–Scherrer camera; the reﬂected beams from a cylindrical

specimen tend towards a focus on the ﬁlm around the circumference of the camera and the focusing

circle for a particular reﬂected beam is shown. In practice deviations from this idealized situation occur

because the reﬂected beams originate with varying intensities from the whole volume of the specimen

and the effective source S may not coincide with the circumference of the camera. (b) The camera with

the light-tight lid removed showing the specimen at the centre, the collimator and receiving tube and

the (low angle) X-ray diffraction rings on the ﬁlm. The screws at the top are for locating and ﬁxing the

ends of the ﬁlm (from Manual of Mineralogy, 21st edn, by C. Klein and C. S. Hurlbut Jr., John Wiley,

1993).

252 X-ray diffraction of polycrystalline materials

the centres of the ‘exit’ and ‘entrance’ rings, the distance between them

on the ﬁlm corresponding to 180

◦

exactly. Hence the camera diameter

does not need to be known, although in practice cameras are made with

diameters 57.53 mm or 114.83 mm such that (and accounting for ﬁlm

thickness) the circumference is 180 mm or 360 mm. Hence for quick

work the angles can simply read in terms of millimetres on the ﬁlm.

It may be thought that the Debye–Scherrer method, as a ﬁlm tech-

nique, has been supplanted by the diffractometer. This is by no means

the case: the ability of examining very small amounts of material and the

conversion of ﬁlm data to digital data via the use of the microdensito-

meter has resulted in its use, for example, in Rietveld analysis (Section

10.6). In addition, ﬁlm may be replaced by an array of position sensitive

detectors in both X-ray and neutron diffraction techniques.

10.3 Some applications of X-ray diffraction

techniques in polycrystalline materials

10.3.1 Accurate lattice parameter measurements

The accurate measurement of d

hkl

-spacings is now largely carried out

with the X-ray diffractometer using monochromatized (Kα

) radiation,

narrow divergence and receiving slit systems, internal calibration systems

and peak proﬁle measurement procedures. However, as shown below, it

is the high 2θ angle reﬂections which are most sensitive to small vari-

ations in d

hkl

-spacings and for this reason the Debye–Scherrer powder

camera and back reﬂection ﬂat ﬁlm techniques in which 2θ angles up

to nearly 180

◦

can be recorded, are still used. By contrast, the largest

2θ angles measurable with a diffractometer are about 150

◦

because the

near approach and possible contact between the source and receiving slit

assemblies.

Given the crystal systemand the hkl values of the reﬂections, thelattice

parameter(s) can be determined using the appropriate equation (Appendix

A4.1). This procedure is clearly simplest for the cubic system in which

the d

hkl

-values depend only upon the one variable, a. In other systems

several d

hkl

-spacings need to be measured and the values inserted into

simultaneous equations from which values of the lattice parameters are

extracted.

Fig. 10.7. An example of a Debye–Scherrer X-ray ﬁlm (CuKα X-radiation) for SiO

(quartz). S is the ‘entrance’ hole and O the ‘exit’ hole. The ‘spotty’ appearance of the

rings arises because of the relatively coarse crystallite size in the specimen. At high

2θ angles (near the entrance hole) the Kα

/Kα

doublets are resolved but at low 2θ

angles (near the exit hole) they are unresolved. The streaks around the exit hole arise

from the presence of residual ‘white’ X-radiation in the incident beam.

10.3 Applications of X-ray diffraction techniques 253

The sensitivity of change of the 2θ angle for a reﬂection with a change in d

hkl

-spacing

is a measure of the resolving power of the diffraction technique. The resolving power,

or rather the limit of resolution, δd /d, can be obtained by differentiating Bragg’s law

with respect to d and θ (λ ﬁxed), i.e.

λ = 2d sin θ

differentiating:

0 = 2d cos θδθ + 2 sin θδd

hence

δd /d =−cot θδθ.

This equation may be ‘read’ in two ways. For a given value of 2δθ, which may be

expressed in terms of the minimum resolved distance between two reﬂections on the

ﬁlm, chart, etc., for the smallest limit of resolution we want cot θ values to be as small as

possible; or, for a given value of δd /d , we want the angular separation of the reﬂections

2δθ to be as large, and hence again cot θ values to be as small as possible.

A glance at cotangent tables shows that cot θ values are high at low θ angles and

rapidly decrease towards zero as θ approaches 90

◦

. Hence d

hkl

-spacing measurements

are most accurate using high-angle X-ray diffraction methods and least accurate with

low-angle electron diffraction methods.

10.3.2 Identiﬁcation of unknown phases

For powder specimens in which the crystals are randomly orientated, the set of d-

spacings and their relative intensities serves as a ‘ﬁngerprint’ (or ‘genetic strand’) from

which the phase can be identiﬁed by comparison with the ‘ﬁngerprints’ of phases in

the X-ray Powder Diffraction File—a data bank of over 250,000 inorganic and 300,000

organic and organometallic phases. The File is administered by the International Centre

for Diffraction Data (ICDD)—formerly the Joint Committee for Powder Diffraction

Standards (JCPDS)—and new and revised sets of data are published annually in book

form (replacing the original 5 inch by 3 inch cards) or as a computer database. In addition,

there are published Indexes with the phases arranged alphabetically by chemical name,

search manuals and abstracts from the File (including Indexes and Search Manuals) or

Frequently Encountered Phases (FEP).

The entry for each phase in the File or computer database (which differ slightly in

their layout) includes: ﬁle number, chemical formula and name, experimental conditions,

physical and optical data (where known), references and the set of d-spacings (given

in Å), their Laue indices and their relative intensities arranged in order of decreasing

d-spacing. Finally, the ICDD editors assign a ‘quality mark’ to indicate the reliability of

the data (e.g. a ‘*’ indicates that the chemistry, structure and X-ray data of the phase is

well characterized); or whether the X-ray data has been derived by calculation, rather