Хаимов 3.С. Основы высшей геодезии

Подождите немного. Документ загружается.

Для получения более полного представления о характере распределения

ошибок измерений и выявления участков, где возможны нарушения нормаль

ного закона, необходимо составить и проанализировать таблицы распреде

лений.

Для этой цели все ошибки группируют в зависимости от величины по

интервалам (разрядам) и подсчитывают их число в каждом интервале. Для

этих же интервалов вычисляют теоретическое число ошибок. Сравнение прак

тического распределения с теоретическим производят путем применения раз

личных «критериев согласия» («критериев соответствия»). Наибольшее рас

пространение из них получили критерий согласия Колмогорова X и критерий

согласия Пирсона х2-

Число и величину разрядов устанавливают в зависимости от цели ис

следования, объема материала и точности произведенных измерений.

Глава 16

УРАВНИТЕЛЬНЫЕ ВЫЧИСЛЕНИЯ

§ 70. ОБЩИЕ СВЕДЕНИЯ ОБ УРАВНИТЕЛЬНЫХ ВЫЧИСЛЕНИЯХ

Уравнивание проводится с целью получения наиболее надеж

ных значений определяемых величин, повышения их точности

и для устранения разногласий в геометрических соотношениях

сети, обусловленных неизбежными ошибками измерений, а так

же для оценки точности измеренных величин и их функций.

Уравнительные вычисления могут быть проведены только

в том случае, если измерений выполнено больше, чем нужно

для определения искомых величин, т. е. когда имеются избы

точные измерения. Поэтому в геодезической практике разли

чают измерения избыточные и необходимые.

Под необходимыми понимают такие измерения, кото

рые позволяют получить только по одному значению определя

емых величин, в то время как избыточные измерения обеспечи

вают получение их нескольких значений. Например, при реше

нии треугольников достаточно иметь одну сторону и два

угла — это и будут необходимые измерения. Если же измерена

сторона и три угла, то один угол — избыточный.

Аналогично в звене триангуляции (рис. 131) с известной

длиной исходной стороны Ь\ и азимутом си и исходным пунк

том А (или двумя исходными пунктами А и В) для определе

ния координат каждого последующего пункта достаточно в тре

угольниках измерить по два угла. Поэтому измерения всех

третьих углов треугольников, а также второй базисной (исход

ной) стороны b2 и ее азимута 0.2 являются избыточными.

Характерной особенностью избыточных измерений является

то, что они обязательно вступают в математические соотноше

ния с другими величинами, в то время как необходимые изме

рения линейно независимы. Например, два угла и сторона тре

угольника никак между собой не связаны, тогда как измерение

каждого третьего угла приводит к математическому соотноше

нию, заключающемуся в том, что сумма трех углов плоского

треугольника должна равняться 180°, а измерения двух сторон

Рис. 131. Необходимые

и избыточные измерения

и двух углов треугольника приводят

к соотношению, выражаемому теоремой

синусов, и т. д.

Избыточные измерения играют боль

шую роль в теории и практике матема

тической обработки геодезических сетей.

Их значение определяется тем, что поз

воляет: а) проводить первичный конт

роль результатов измерений с целью вы

явления грубых ошибок и промахов;

б) контролировать качество проводимых измерений по невяз

кам условных уравнений, а также установлением для них соот

ветствующих предельных допусков; в) повышать точность опре

деления отдельных элементов сети путем использования мно

гократных измерений и обработки по методу наименьших

квадратов; г) проводить оценку точности измеренных величин

и их функций; д) судить о правильности применяемой методики

измерений по соответствию полученной точности с заданной.

При уравнивании геодезических сетей большое значение

имеет ее вид — свободная или несвободная сеть.

Свободными сетями называют такие геодезические сети

(рис. 132, а), которые имеют только необходимое число исход

ных данных. Например, в триангуляции свободными будут сети,

имеющие только один исходный пункт и одну исходную сто

рону с измеренной длиной и азимутом или координаты только

двух исходных пунктов. Они полностью определяют положение,

масштаб и ориентировку сети.

Несвободными называют сети (рис. 132,6), имеющие

избыточное число исходных данных, а именно: координаты не

скольких несмежно расположенных исходных пунктов, два и

более базисов и азимутов. Обычно строятся несвободные сети.

Государственная плановая геодезическая сеть является несво

бодной сетью. Однако в инженерной практике встречаются и

свободные сети.

Уравнительные вычисления могут проводиться строгими или

приближенными способами.

Рис. 132. Схема свободных (а) и несво

бодных (б) сетей

Строгие способы уравнивания должны удовлетворять сле

дующим требованиям:

) после уравнивания должны быть со

блюдены все геометрические условия сети, т. е. ликвидированы

все невязки;

) найденные поправки в измеренные величины

Vi должны удовлетворять принципу наименьших квадратов,

т. е.

ру

= min (р — вес измеренной величины); 3) должно

соблюдаться условие совместной обработки всех измеренных

величии сети; 4) должна быть обеспечена возможность оценки

точности различных элементов уравненной сети.

Строгие методы уравнивания проводятся по методу наи

меньших квадратов.

В приближенных способах уравнивания соблюдается

только требование удовлетворения геометрических условий сети.

Остальные требования не выполняются или соблюдаются лишь

приближенно.

Все способы уравнивания вычислений можно разделить на

две основные группы.

Одну группу составляют методы, основанные на коррелат-

ном способе*, вторую — на параметрическом**.

В коррелатном способе решается задача на условный экст

ремум — отыскание минимума функции Upv2 с использованием

вспомогательных неизвестных — коррелат. При этом состав

ляют независимые условные уравнения, вытекающие из геомет

рических соотношений сети, и из уравнивания отыскивают по

правки к непосредственно измеренным величинам (углам, на

правлениям или сторонам).

В параметрическом способе решается задача на абсолютный

экстремум — отыскание минимума той же функции Zpv2. В ка

честве неизвестных в нем выбираются такие неизвестные — па

раметры, в функции которых могут быть выражены все изме

ренные величины. При этом составляют уравнения поправок и

из уравнения находят сначала поправки к этим параметрам,

являющиеся, в свою очередь, функциями непосредственно из

меренных величин, а затем — поправки к самим измеренным

величинам.

Допустим, что требуется определить п величин Х\\ Х2, ...

..., Хп. В результате измерений получены их значения Х\, х2, . ..

..., хп с весами ри р2, ..., рп, т. е. произведено п измерений, из

которых k — число необходимых, г — избыточных измерений,

n = k + r. Так как все избыточные измерения входят с необходи

мыми в определенные математические соотношения, то в ре

зультате уравнивания должны быть найдены такие значения

неизвестных, которые удовлетворяли бы всем этим математи

ческим связям.

При этом можно поступить двояким образом.

* Ранее назывался способ условных измерений.

** Ранее назывался метод посредственных (косвенных) измерений или

способ необходимых неизвестных.

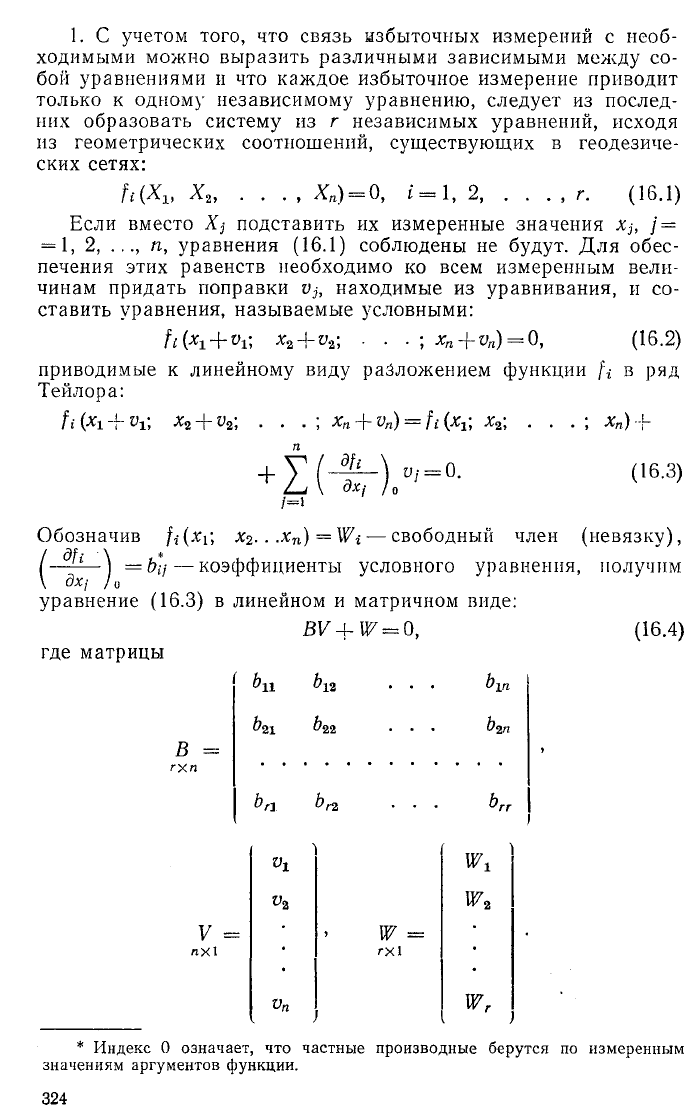
1. С учетом того, что связь избыточных измерений с необ

ходимыми можно выразить различными зависимыми между со

бой уравнениями и что каждое избыточное измерение приводит

только к одному независимому уравнению, следует из послед

них образовать систему из г независимых уравнений, исходя

из геометрических соотношений, существующих в геодезиче

ских сетях:

f{(Xlt Х2, = О, i = l, 2

.................

г. (16.1)

Если вместо Xj подставить их измеренные значения Xj, / =

= 1, 2, ..., п, уравнения (16.1) соблюдены не будут. Для обес

печения этих равенств необходимо ко всем измеренным вели

чинам придать поправки Vj, находимые из уравнивания, и со

ставить уравнения, называемые условными:

fi(x! + Vi, x2 + v2-, • ■ • ; xn + vn) = Q, (16.2)

приводимые к линейному виду разложением функции в ряд

Тейлора:

fi(x x i~rvi\ • • ■ ; хп vn) = fi (хij x2\ . . . ; xn)-\-

+ 1

/=i

dft

l / о

Vj = 0. (16.3)

Обозначив fi(x i; X2...x n) = Wi-—свободный член (невязку),

df ’ \ *

— bi

— коэффициенты условного уравнения, получим

дх

I / о

уравнение (16.3) в линейном и матричном виде:

BV + W = 0, (16.4)

где матрицы

6ц Ь12 . . . bin

В :

ГХП

и22

гаХ1

Ьп

Ьг2 . . .

brr

w x

w t

•

W =

rxl

w r

* Индекс 0 означает, что частные производные берутся по измеренным

значениям аргументов функции.

В г уравнениях (16.2) п неизвестных поправок, при этом

всегда г<п, поэтому, чтобы сделать задачу определенной, при

меняют метод наименьших квадратов, т. е. решение осуществ

ляют под условием VTPV = [pu2] = min, для чего вводят вспомо

гательную функцию Лагранжа:

F = VTPV — 2KT(BV + W) (16.5)

и находят ее минимум, сводящийся к составлению п уравнений

с г неизвестными:

- ^ ^ Р У — ВТК = 0, (16.6)

где К = {К\, К2, ■ ■ ■, Кг} — вспомогательные неизвестные — кор-

релаты; Р = {ри р2, ..., рп} — диагональная матрица весов.

Совместное решение п + r уравнений (16.3) и (16.6) с (п + г)

неизвестными (поправками и коррелатами) осуществляется пу

тем составления нормальных уравнений коррелат NK+W = 0,

где N = BQBT и Q = P~l — матрица обратных весов, равная

{Яи Я% ■ • •> Яп}, Яз = 1/pj» и определения коррелат К = —N~lW,

а затем искомых поправок V = QBTK = —QBTN~lW и уравнен

ных значений искомых величин:

Xj — Xj^Vj. (16.7)

Так проводится уравнивание коррелатным методом.

2. Выбирают k неизвестных параметров Т, в функции кото

рых могут быть выражены все искомые величины, т. е.

Xi = fi(Tlt Т2

.................

П), /= 1, 2, . . п. (16.8)

Если вместо Xj подставить измеренные значения Xj, получен

ные с весом pj, равенство (16.8) выполняться не будет, но

можно составить п уравнений поправок вида

fiifu 4 • • • , Q —Xj = vh (16.9)

где t\ , (2', . - tk' — уравненные значения параметров. Уравнен

ные значения измеренных величин будут х/ = Xj + vj.

В общем случае функция fj имеет нелинейный вид. Для ее

линеаризации находят приближенные значения параметров f

и представляют неизвестные в виде

^ ==^Н“'С/г> k= \, 2 , . . . , k, (16.10)

где tk°— приближенные значения неизвестных; хи— поправки

к ним.

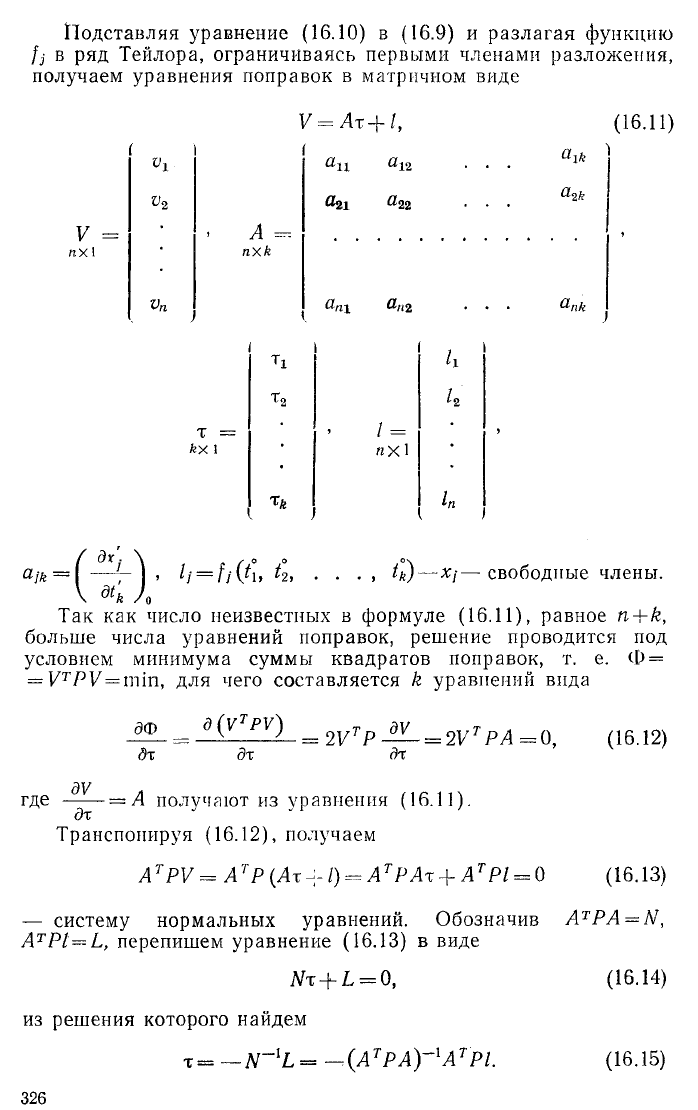
Подставляя уравнение (16.10) в (16.9) и разлагая функцию

fi в ряд Тейлора, ограничиваясь первыми членами разложения,

получаем уравнения поправок в матричном виде

»1

V =

А -

ПХ 1

n x k

V = Ах+1,

аи av&

#2i ^22

(16.11)

alk

&n\ 0/12

® -n k

dx;

X =

1 =

kx 1

пх 1

Ч In

li = f i( t ь h, . . . . Q

свободные члены.

k /о

Так как число неизвестных в формуле (16.11), равное n + k,

больше числа уравнений поправок, решение проводится под

условием минимума суммы квадратов поправок, т. е. Ф =

= VTP V =min, для чего составляется /г уравнений вида

Эф _ d(VTPV) = 2 у тр М

дт

дг

■■2VT Р А =0,

(16.12)

где

дх

■ А получают из уравнения (16.11).

Транспонируя (16.12), получаем

АтPV = ArР (Ах1) = АтРАх + АтР1 = 0

(16.13)

— систему нормальных уравнений. Обозначив ATPA = N,

ATPt=L, перепишем уравнение (16.13) в виде

Nx + L = 0,

из решения которого найдем

-N~'L= —(ATP A )-lArPl.

(16.14)

(16.15)

После чего определим поправки V из уравнения (16.11), а так

же значения параметров t' — t + x и неизвестных x' = xj + vj.

В этом заключается сущность параметрического метода урав

нивания. В геодезических сетях в качестве параметров удобно

выбирать координаты пунктов.

Уравнительные вычисления завершаются оценкой точности

уравненных величин и их функций [1].

§ 71. КОРРЕЛАТНЫИ СПОСОБ УРАВНИВАНИЯ.

УСЛОВНЫЕ УРАВНЕНИЯ, ВОЗНИКАЮЩИЕ

В СВОБОДНЫХ СЕТЯХ ТРИАНГУЛЯЦИИ

В основе этого способа лежит составление условных уравнений.

Рассмотрим коррелатный способ на примере уравнивания три

ангуляции.

В сетях триангуляции измеряют либо углы, либо направле

ния, поэтому и уравнивание проводится по углам или направ

лениям. Однако на практике часто уравнивание проводят по

углам и тогда, когда измерены направления. Объясняется это

тем, что при уравнивании по углам число независимых попра

вок по сравнению с уравниванием по направлениям сокраща

ется в два раза, а это значительно облегчает вычисления. Но

следует помнить, что такое уравнивание будет приближенным.

Упрощенным будет также независимое раздельное уравнивание

сплошной сети по частям, элементы которой взаимосвязаны.

Математические соотношения, определяющие условные урав

нения, зависят от вида сети, от того, является она свободной

или несвободной. Поэтому различают условия, возникающие

в свободных и несвободных сетях.

В дальнейшем предполагается, что все измерения равно

точны, приведены к центрам пунктов и редуцированы на

плоскость. Называться они будут измеренными величинами.

В свободных сетях триангуляции могут возникать: 1) усло

вия фигур, 2) условия горизонтов, 3) условия полюсов.

1. Условия фигур. Условные уравнения фигур, или, как их

кратко называют, условия фигур, возникают в замкнутых гео

метрических фигурах со всеми измеренными углами и основаны

на том, что сумма углов любого многоугольника равняется

180° • (п—2), где п — число вершин многоугольника.

Однако вследствие ошибок измерений сумма углов п-уголь-

ника, составленная из измеренных величин, никогда не будет

равняться теоретическому значению.

Задачей уравнивания является нахождение таких поправок

ко всем измерениям, которые обеспечили бы соблюдение дан

ного геометрического условия.

Условия фигур при уравнивании по углам. Пусть

в треугольнике ABC (рис. 133) 1, 2, 3 — измеренные углы,

a V\, V2, Vz — поправки к ним. Тогда условие фигуры треуголь

ника, состоящее в том, что сумма его углов равна 180°, будет

Рис. 133. Схема составления услов- Рис. 134. Схема составления услов

ного уравнения фигуры в треуголъ- ного уравнения горизонта

нике

соблюдено, если всем измеренным углам придать соответствую

щие поправки viy т. е.

l-lr v1-r 2-[-y2-f 3 + t>3 = 180: или

vi + v2 + + {(1 + 2 + 3)— 180°} =0.

Обозначая величину, заключенную фигурными скобками, на

зываемую свободным членом условного уравнения или невяз

кой W треугольника, получим окончательный вид условия фигур

+ Уз+ W = 0, (16.16)

где W— 1 + 2 + 3—180° вычисляют по измеренным аргументам.

Искомые поправки часто обозначают арабской цифрой

в скобках, поэтому уравнение (16.16) может быть записано так:

(У) + (2)-;-(3) + Г = 0. (16.17)

Аналогично пишут условные уравнения и для более сложных

замкнутых геометрических фигур.

Условия фигур при уравнивании по направлениям.

В этом случае каждый угол заменяется разностью двух направ

лений и поправки вводят в направления.

Пусть в треугольнике ABC (см. рис. 133) измерены направ

ления Г, 2', 3', 4', 5', 6 '. Поправки к ним соответственно будут

Vi> v^ v5, v6. Тогда условное уравнение будет

(2 +Uj[) — (Г + Vj) + (4' + v4) (3/ + ds) +

+ue)

— (5' + у5)=180° или —Vi + u

—U

+ U

— y

+ o6+ 117 = 0, (16.18)

где Г== — Г + 2’ — 3’ + 4’ — 5’+

’ — 180°.

Для удобства вычислений на каждом пункте направления

нумеруют по ходу часовой стрелки, а поправки в условном

уравнении располагают по возрастающим номерам.

2. Условие горизонта. Условные уравнения горизонта (ус

ловия горизонта) возникают в случае измерения углов на

пункте по всему горизонту, а также во всех центральных систе

мах с измеренными углами (рис. 134). Условие заключается

в том, что сумма уравненных углов на пункте должна рав

няться 360°.

При уравнивании по углам условное уравнение горизонта

будет иметь вид

т. е. условие будет соблюдено только после того, когда

всем измеренным углам будут приданы соответствующие по

правки, найденные из уравнивания. Условие (16.19) может

быть записано так:

где Wq= 1+ 2 + 3 + 4 + 5—360° — свободный член условия гори

зонта (известная величина, вычисленная по измеренным дан

ным).

При уравнивании направлений условия горизонта не

возникают, так как всегда сумма углов, образованных разно

стью направлений, равна нулю. Однако если измеряли направ

ления, а уравнивание будет проводиться по углам, то услов

ное уравнение составляют и включают в общую систему урав

нений со свободным членом, равным нулю.

3. Полюсные условия. Они возникают в замкнутых фигурах,

в которых можно независимыми путями дважды вычислить

одну и ту же сторону.

Полюсные условия возникают в центральных системах, гео

дезических четырехугольниках (рис. 135, а, б) и фигурах с из

быточными диагональными направлениями (рис. 135, в). За

ключается оно в том, что в уравненной сети длины одной и той

же стороны, вычисленные дважды из решения различных тре

угольников, должны совпадать. Если не поставить такого ус

ловия, совпадения сторон не произойдет, так как уравнивание

только за угловые условия еще не определяет размеры геомет

рических фигур, ибо можно получить ряд подобных фигур

с равными углами и разными сторонами.

Рис. 135. Схема составления полюсного (бокового) условного уравнения

1 -\-Vi~\- 2 3 -\-v3-{-4 5 -\-v5 — 360°, (16.19)

V1 + V1 + V3 + Vi ' f V5 + Wq — 0.

(16.19a)

Пусть в геодезическом четырехугольнике ABCD (см.

рис. 135,6) известна сторона АС и измерены углы 1, 2, 3, 4, 5,

6 , 7, 8 . Поправки углов будут соответственно равны Vi, V2, v3,

viy us, ve, vr, v8. Исходную сторону AC мы можем вторично вы

числить, решив последовательно треугольники ABC, ADB,

ACD. Однако по измеренным углам мы получим другое ее

значение. Чтобы ликвидировать это расхождение, необходимо

всем измеренным углам придать соответствующие поправки.

Тогда получим функцию

sin (3 -f- р8) sin (5 -f-ti5) sin (7 -f-1>7 -f- 8 -f- pg) _ (16 20)

sin (8 + v3) sin (3 + »s 4 + ) sin (6 -{- ^e)

Разделив на AC, получим выражение полюсного условия в виде

отношения синусов углов

sin (3 -|- а3) sin (5 -|- и5) sin (7 + ^7 + 8 + o8J

___

j ^20 2 J)

sin (8 + vs) sin (3 -]- vs -f- 4 + t>4) sin (6 + ve)

Заменяя отношения синусов отношением противоположных сто

рон, полюсное условие (16.21) можно написать в виде тож

дества

_АС_ _AD__AB_= l ^ (16.22)

AD АВ AC v

На практике оказывается удобным начинать составлять по

люсное условие именно с отношения сторон, исходящих из од

ной точки (полюса), начиная и кончая одной и той же сторо

ной, а затем заменяя отношения сторон отношением синусов

противолежащих в данном треугольнике углов. Это позволяет

контролировать составление условия тем, что после сокращения

одинаковых сторон в левой части уравнения также должна

быть единица.

Полученная форма полюсного условия имеет нелинейный

вид и неудобна для вычислений. Поэтому ее приводят к линей

ному виду. Для этого в соответствии с уравнением (16.3) най

дем частные производные функции F по всем аргументам |3j

исходя из формулы

( - f - ) = ± 4 C c tg fr -v - <16-23)

V % /о р"

(плюс для членов числителя, минус — для знаменателя) и оп

ределим свободный член

W^AC( sin3sin5sin(7 + 8-) _ П . (16.24)

\ sin 8 sin (3 + 4) sin 6 }