Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

Chapter Three

Stability Theory for Nonlinear

Dynamical Systems

3.1 Introduction

One of the most basic issues in system theory is stability of dynamical

systems. System stability is characterized by analyzing the response of a

dynamical system to small perturbations in the system states. Speciﬁcally,

an equilibr ium point of a dynamical system is said to be stable if, for

suﬃciently small values of initial disturbances, the perturbed motion

remains in an arbitrarily prescribed small region of the state space. More

precisely, stability is equivalent to continuity of solutions as a function

of the system initial conditions over a neighborhood of the equilibrium

point uniformly in time. If, in addition, all solutions of the dynamical

system approach the equilibrium point for large values of time, then the

equilibrium point is said to be asymptotically stable. The most complete

contribution to the stability analysis of nonlinear dynamical systems was

introduced in the late nineteenth century by the R ussian mathematician

A. M. Lyapun ov in his seminal work entitled The General Problem of

the Stability of Motion [293–295]. Lyapunov’s r esults which include the

direct and indirect methods, along w ith the Barbashin -Krasovskii-LaSalle

invariance principle [23, 245, 258, 260], provide a powerful framework for

analyzing the stability of nonlinear dynamical systems as well as designing

feedback controllers that guarantee closed-loop system stability.

Lyapunov’s direct method states that if a continuously diﬀerentiable

positive-deﬁnite function of the states of a given dynamical system can be

constructed for which its time rate of change d ue to perturbations in a

neighborhood of the system’s equilibrium is always n egative or zero, then

the system’s equilibrium point is stable or, equivalently, Lyapunov stable.

Alternatively, if the time rate of change of the positive-deﬁnite function

is strictly negative, then th e system’s equilibrium point is asymptotically

stable. Unlike L yapunov’s direct method, which can provide global stability

conclusions for an equilibrium point for a non linear dynamical system,

NonlinearBook10pt November 20, 2007

136 CHAPTER 3

Lyapunov’s indirect method draws conclusions about local stability of the

equilibrium point by examining the stability of the linearized nonlinear

system about the equilibrium point in question. Since the analysis and

controller design frameworks presented in this book are predominantly based

on Lyapunov stability theory, in this chapter we present the main Lyapunov

stability results needed for developing these frameworks.

3.2 Lyapunov Stability Theory

In this section, we develop the fundamental results of Lyapunov stability

theory. We begin by considering the general nonlinear autonomous

dynamical system

˙x(t) = f(x(t)), x(0) = x

, t ∈ I

, (3.1)

where x(t) ∈ D ⊆ R

, t ∈ I

, is the s y s tem state vector, D is an open set

with 0 ∈ D, f : D → R

is continuous on D, and I

= [0, τ

), 0 ≤ τ

≤ ∞.

We assume that for every initial condition x(0) ∈ D and every τ

> 0, the

dynamical system (3.1) possesses a unique solution x : [0, τ

) → D on the

interval [0, τ

). We denote the solution to (3.1) with initial condition x(0) =

by s(·, x

), s o that the ﬂ ow of the dynamical sys tem (3.1) given by the

map s : [0, τ

) × D → D is continuous in x and continuously diﬀerentiable

in t and satisﬁes the consistency property s(0, x

) = x

and the semigroup

property s(τ, s(t, x

)) = s(t + τ, x

), for all x

∈ D and t, τ ∈ [0, τ

) such

that t + τ ∈ [0, τ

). Unless otherwise stated, we assume f(0) = 0 and f (·)

is Lipschitz continuous on D. The following deﬁnition introduces several

types of s tability corresponding to the zero solution x(t) ≡ 0 of (3.1) for

= [0, ∞).

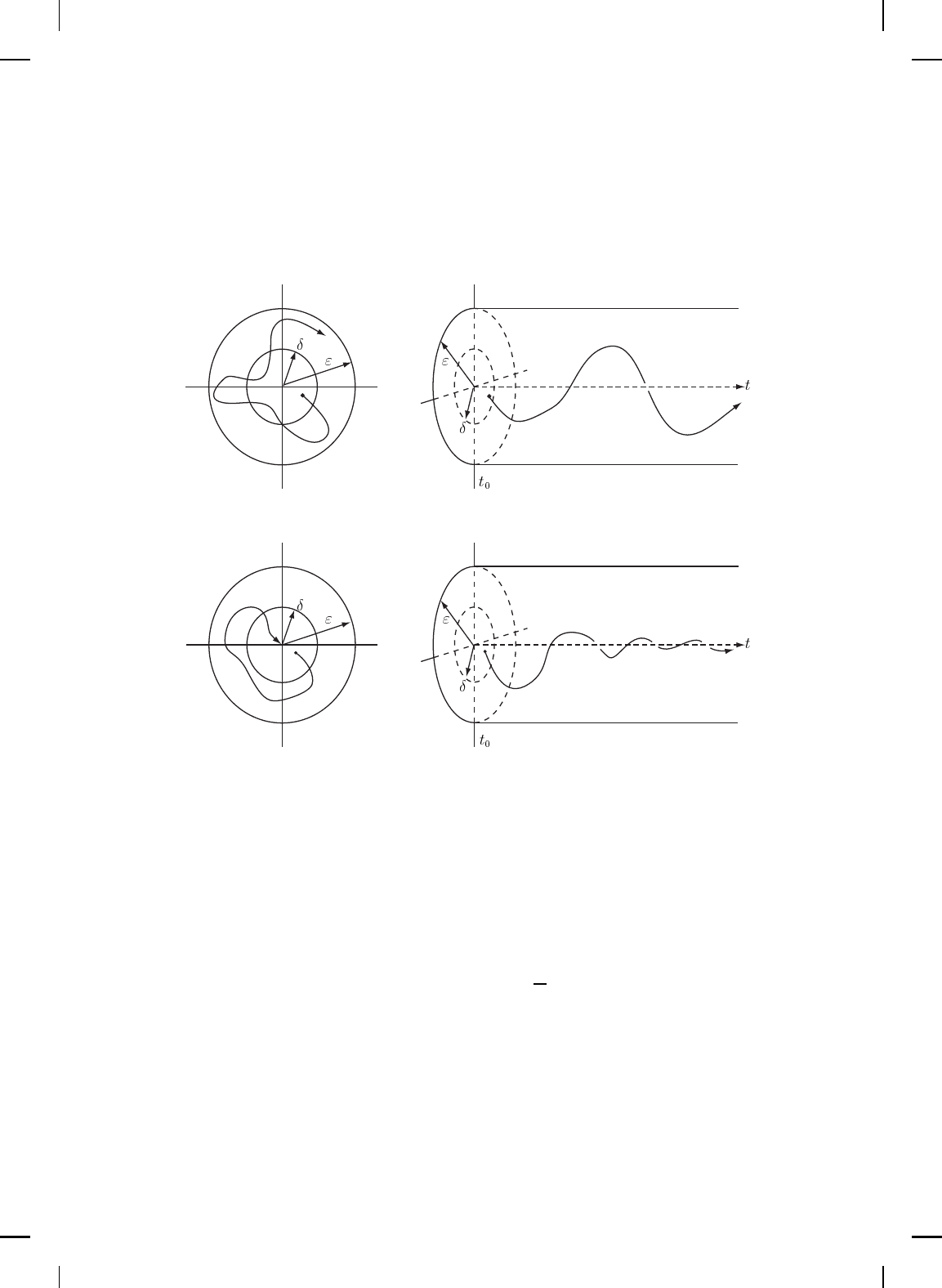
Deﬁnition 3.1. i) The zero solution x(t) ≡ 0 to (3.1) is Lyapunov

stable if, for all ε > 0, there exists δ = δ(ε) > 0 such that if kx(0)k < δ, then

kx(t)k < ε, t ≥ 0 (see Figure 3.1).

ii) The zero solution x(t) ≡ 0 to (3.1) is (locally) asymptotically stable

if it is Lyapunov stable and there exists δ > 0 such that if kx(0)k < δ, then

lim

t→∞

x(t) = 0 (see Figure 3.2).

iii) The zero solution x(t) ≡ 0 to (3.1) is (locally) exponentially stable

if there exist positive constants α, β, and δ such that if kx(0)k < δ, then

kx(t)k ≤ αkx(0)ke

−βt

, t ≥ 0.

iv) The zero solution x(t) ≡ 0 to (3.1) is globally asymptotically stable

if it is Lyapunov stable and for all x(0) ∈ R

, lim

t→∞

x(t) = 0.

v) The zero solution x(t) ≡ 0 to (3.1) is globally exponentially stable

NonlinearBook10pt November 20, 2007

STABILITY THEORY FOR NONLINEAR SYSTEMS 137

if there exist positive constants α and β such that kx(t)k ≤ αkx(0)ke

−βt

t ≥ 0, for all x(0) ∈ R

vi) Finally, the zero solution x(t) ≡ 0 to (3.1) is unstable if it is not

Lyapunov s table.

Figure 3.1 Lyapunov stability of an equilibrium point.

Figure 3.2 Asymp totic stability of an equilibrium point.

Figure 3.3 shows the asymptotic stability, Lyapunov stability, and

instability notions of an equ ilibr ium point. Clearly, exponential stability

implies asymptotic stability and asymptotic stability implies Lyapunov

stability. The following result, kn own as Lyapunov’s direct method, gives

suﬃcient conditions for Lyapunov, asymptotic, and exponential s tability of a

nonlinear dynamical sys tem. For this result, let V : D → R be a continuously

diﬀerentiable function with derivative along the trajectories of (3.1) given

V (x)

△

= V

′

(x)f(x). Note that

V (x) is dependent on the system dynamics

(3.1). Since, using the chain rule,

V (x) =

V (s(t, x))



t=0

= V

′

(x)f(x)

it follows that if

V (x) is negative, then V (x) decreases along the solution

s(t, x

) of (3.1) through x

∈ D at t = 0.

Theorem 3.1 (Lyapunov’s Theorem). Consider the nonlinear dynam-

ical system (3.1) and assume that there exists a continuously diﬀerentiable

NonlinearBook10pt November 20, 2007

138 CHAPTER 3

Lyapunov Stable

Unstable

Asymptotically

Stable

∂B

(0)

∂DD

(0)

Figure 3.3 Asymp totically stable, Lyapunov stable, and unstable equilibrium point.

function V : D → R such that

V (0) = 0, (3.2)

V (x) > 0, x ∈ D, x 6= 0, (3.3)

′

(x)f(x) ≤ 0, x ∈ D. (3.4)

Then the zero solution x(t) ≡ 0 to (3.1) is Lyapunov stable. If, in addition,

′

(x)f(x) < 0, x ∈ D, x 6= 0, (3.5)

then the zero solution x(t) ≡ 0 to (3.1) is asymptotically stable. Finally, if

there exist scalars α, β, ε > 0, and p ≥ 1, such that V : D → R satisﬁes

αkxk

≤ V (x) ≤ βkxk

, x ∈ D, (3.6)

′

(x)f(x) ≤ −εV (x), x ∈ D, (3.7)

then the zero solution x(t) ≡ 0 to (3.1) is exponentially stable.

Proof. Let ε > 0 be such that B

(0) ⊆ D. Since ∂B

(0) is compact

and V (x), x ∈ D, is continuous, it follows that V (∂B

(0)) is compact (see

Proposition 2.14), and hence, by Theorem 2.13, α

△

= min

x∈∂B

(0)

V (x) exists.

Note α > 0 since 0 6∈ ∂B

(0) and V (x) > 0, x ∈ D, x 6= 0. Next, let

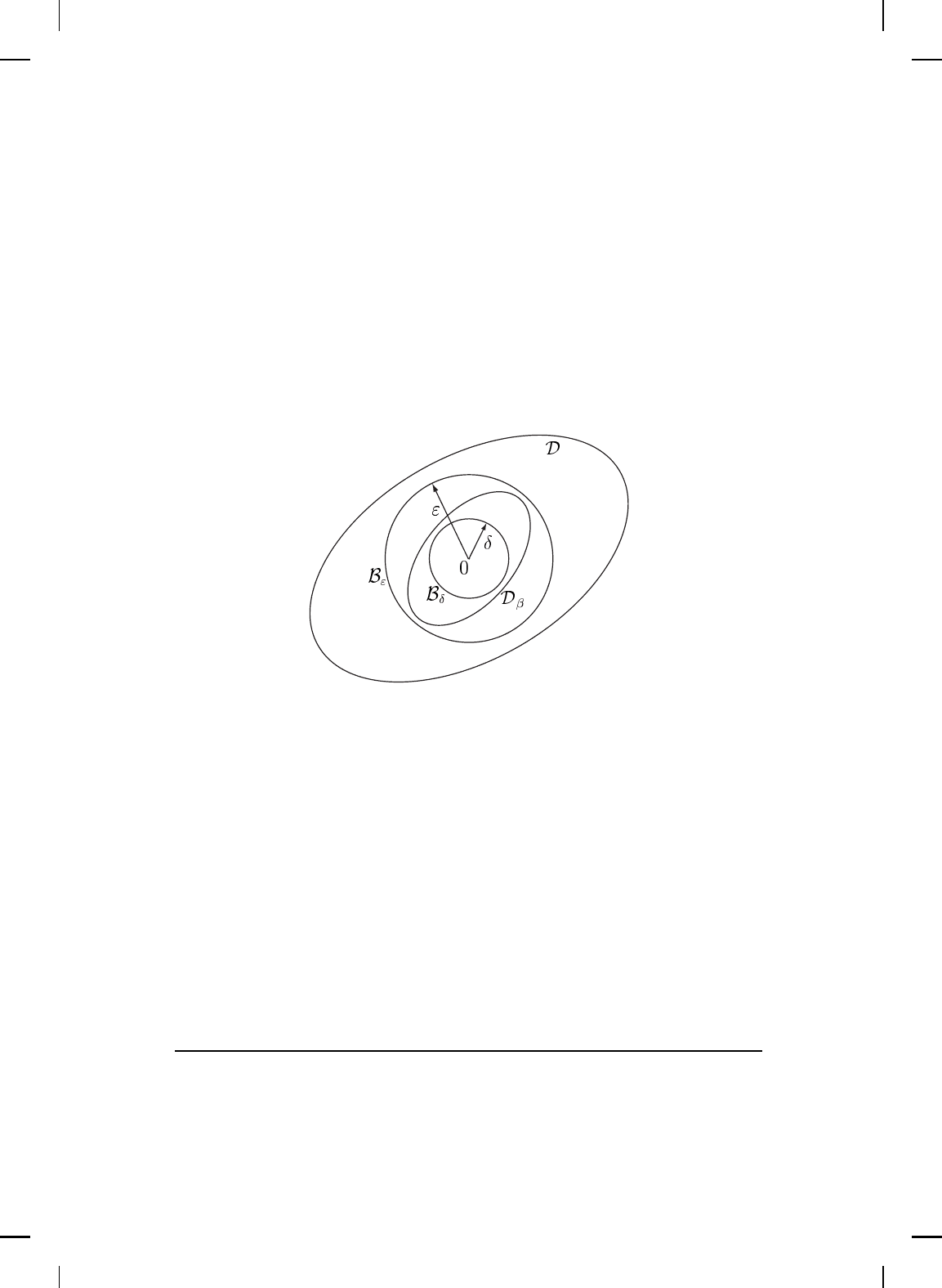
NonlinearBook10pt November 20, 2007

STABILITY THEORY FOR NONLINEAR SYSTEMS 139

β ∈ (0, α) and deﬁne D

to be the arcwise connected component of {x ∈ D :

V (x) ≤ β} containing the origin; that is, D

is the set of all x ∈ D such

that there exists a continuous fun ction ψ : [0, 1] → D such that ψ(0) = x,

ψ(1) = 0, and V (ψ(µ)) ≤ β, for all µ ∈ [0, 1].

Note that D

⊂ B

(0)

(see Figure 3.4). To see this, suppose, ad absurdum, that D

6⊂ B

(0). In

this case, there exists a point p ∈ D

such that p ∈ ∂B

(0), and hence,

V (p) ≥ α > β, which is a contradiction. Now, since

V (x)

△

= V

′

(x)f(x) ≤ 0,

x ∈ D

, it follows that V (x(t)) is a nonincreasing function of time, and

hence, V (x(t)) ≤ V (x(0)) ≤ β, t ≥ 0. Hence, D

is a positively invariant

set with respect to (3.1). Furthermore, since D

is compact, it follows from

Corollary 2.5 that for all x(0) ∈ D

, (3.1) has a unique solution deﬁned for

all t ≥ 0.

Figure 3.4 Visualization of sets used in the proof of Theorem 3.1.

Next, since V (·) is continuous and V (0) = 0, there exists δ = δ(ε) ∈

(0, ε) such that V (x) < β, x ∈ B

(0). Now, let x(t), t ≥ 0, satisfy (3.1) with

kx(0)k < δ. Since, B

(0) ⊂ D

⊂ B

(0) ⊆ D and V

′

(x)f(x) ≤ 0, x ∈ D, it

follows that

V (x(t)) − V (x(0)) =

′

(x(s))f(x(s))ds ≤ 0, t ≥ 0,

and h en ce, for all x(0) ∈ B

(0),

V (x(t)) ≤ V (x(0)) < β, t ≥ 0.

Now, since V (x) ≥ α, x ∈ ∂B

(0), an d β ∈ (0, α), it follows that x(t) 6∈

∂B

(0), t ≥ 0. Hence, for all ε > 0 there exists δ = δ(ε) > 0 such that if

kx(0)k < δ, then kx(t)k < ε, t ≥ 0, w hich proves Lyapunov stability of the

zero solution x(t) ≡ 0 to (3.1).

Unless otherwise stated, in the remainder of the book we assume that sets of the form D

{x ∈ D : V (x) ≤ β} correspond to the arcwise connected component of {x ∈ D : V (x) ≤ β}

containing the origi n. This minor abuse of notation considerably simpliﬁes the presentation.

NonlinearBook10pt November 20, 2007

140 CHAPTER 3

To prove asymptotic stability of the zero solution x(t) ≡ 0 to (3.1)

suppose that V

′

(x)f(x) < 0, x ∈ D, x 6= 0, and x(0) ∈ B

(0). Then it

follows that x(t) ∈ B

(0), t ≥ 0. However, V (x(t)), t ≥ 0, is decreasing and

bounded from below by zero. Now, ad absurdum, suppose x(t), t ≥ 0, does

not converge to zero. This implies that V (x(t)), t ≥ 0, is lower bounded,

that is, there exists L > 0 such that V (x(t)) ≥ L > 0, t ≥ 0. Hence, by

continuity of V (·) there exists δ

′

> 0 such that V (x) < L for x ∈ B

′

(0),

which further implies that x(t) 6∈ B

′

(0) for all t ≥ 0. Next, deﬁne L

△

min

′

≤kxk≤ε

−V

′

(x)f(x). Now, (3.5) implies −V

′

(x)f(x) ≥ L

, δ

′

≤ kxk ≤ ε

or, equivalently,

V (x(t)) − V (x(0)) =

′

(x(s))f(x(s))ds ≤ −L

and h en ce, for all x(0) ∈ B

(0),

V (x(t)) ≤ V (x(0)) − L

Letting t >

V (x(0))−L

, it follows that V (x(t)) < L, which is a contradiction.

Hence, x(t) → 0 as t → ∞, establishing asymptotic stability.

Finally, to prove exponential stability of the zero solution x(t) ≡ 0 to

(3.1) note that (3.7) implies

V (x(t)) ≤ V (x(0))e

−εt

, t ≥ 0. (3.8)

Now, sin ce by assumption V (x(0)) ≤ βkx(0)k

and αkx(t)k

≤ V (x(t)), it

follows that

αkx(t)k

≤ βkx(0)k

−εt

, t ≥ 0, (3.9)

which implies that

kx(t)k ≤





1/p

kx(0)ke

(−ε/p)t

, t ≥ 0, (3.10)

establishing exponential stability.

If x

6= 0 is an equilibrium point of (3.1), then Theorem 3.1 holds with

V (0) = 0 and x 6= 0 replaced by V (x

) = 0 and x 6= x

(see Problem 3.39

for details). A continuously diﬀerentiable function V (·) satisfying (3.2) and

(3.3) is called a Lyapunov function candidate for the nonlinear dynamical

system (3.1). If, additionally, V (·) satisﬁes (3.4), V (·) is called a Lyapunov

function for the nonlinear dynamical system (3.1).

In light of conditions (3.2)–(3.5), V (·) can be regarded as a generalized

energy function for the nonlinear dynamical system (3.1). In particular,

viewing the Lyapunov level surfaces V (x) = α, for suﬃciently small

constants α > 0, as constant energy surfaces covering th e neighborhood

⊂ B

(0), where V (x

) = β, of the non linear dyn amical system (3.1), it

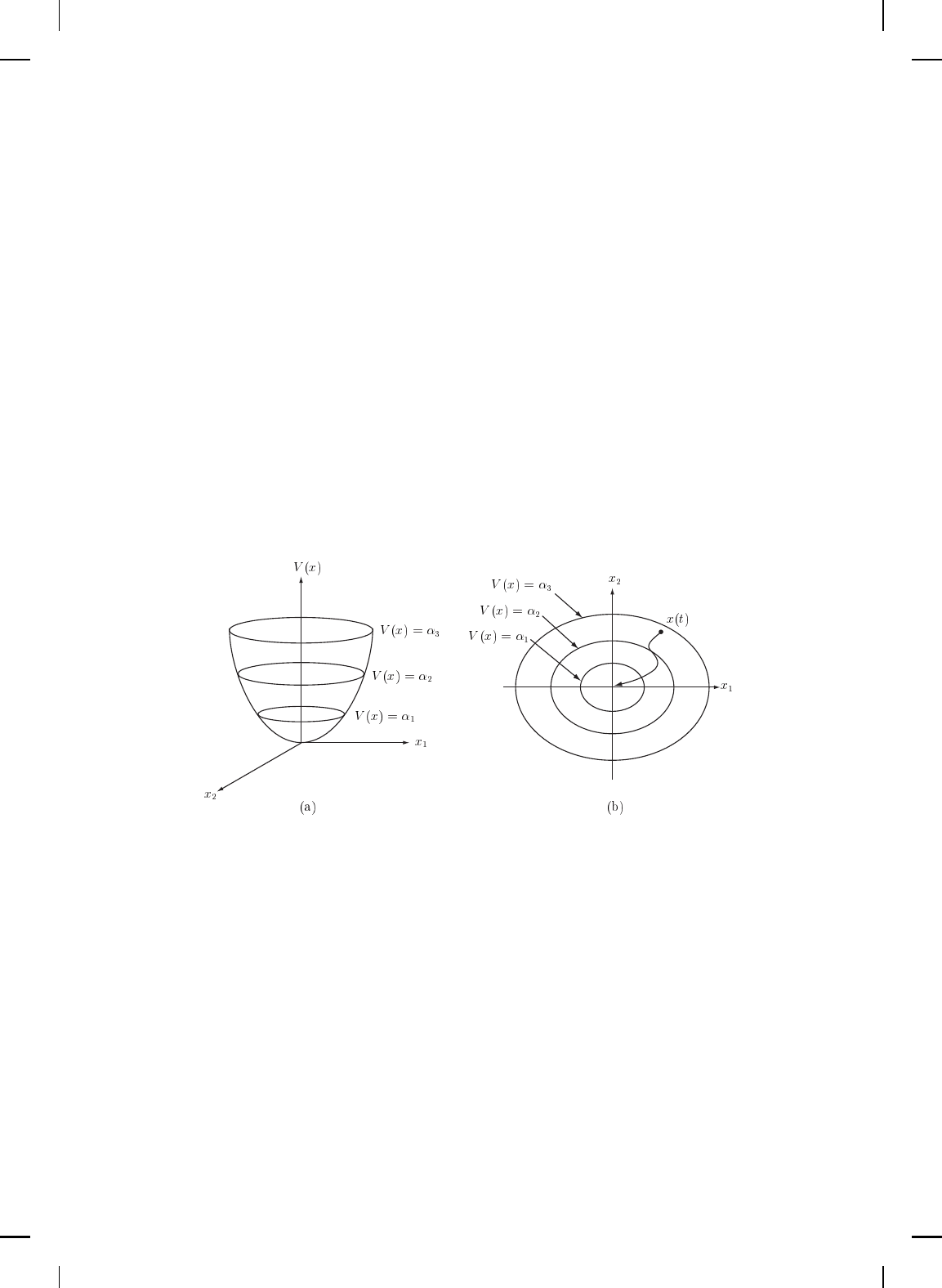
NonlinearBook10pt November 20, 2007

STABILITY THEORY FOR NONLINEAR SYSTEMS 141

follows from Theorem 3.1 that r equ ir ing the Lyapunov derivative

V (x)

△

′

(x)f(x) to be negative, the system traj ectories of (3.1) move from one

energy surface to an inner, or lower, en ergy surface. Of course, if condition

(3.4) is satisﬁed, the system trajectories will approach the origin and remain

within a ball of radiu s ε > 0 of the origin for every sys tem initial condition

lying inside a constant energy surface contained in the ball of radius ε.

Alternatively, if condition (3.5) is satisﬁed, then the system’s energy surfaces

shrink to zero so that the system trajectory approaches zero asymptotically

(see Figure 3.5).

For planar (R

) systems the Lyapunov function provides the following

interpretation. For a given solution s(t, x

) of (3.1) to cross the constant

energy surface V (x) = β, w here β = V (x

), the angle between the outward

normal of the gradient vector V (x

) and the derivative of s(t, x

) at t = t

must be greater than π/2, that is,

V (x

) = V

′

)f(x

) < 0. For this to

occur at all points, we require

V (x) = V

′

(x)f(x) < 0, x ∈ D

. Hence,

V (s(t, x

)) is a decreasing function of time. This of course implies that

V (s(t, x)) along the solution s(t, x

) of (3.1) must be negative in D

Figure 3.5 (a) Typical Lyapunov function candidate. (b ) Constant Lyapunov energy

surfaces. For both ﬁgures α

< α

Example 3.1. Consider the nonlinear dynamical system representing

a rigid spacecraft given by

˙x

(t) = I

(t)x

(t), x

(0) = x

, t ≥ 0, (3.11)

˙x

(t) = I

(t)x

(t), x

(0) = x

, (3.12)

˙x

(t) = I

(t)x

(t), x

(0) = x

, (3.13)

where I

= (I

− I

)/I

, I

= (I

− I

)/I

, I

= (I

− I

)/I

, and I

are the principal moments of inertia of the spacecraft such that

> I

> 0. To examine the stability of this system consider the

NonlinearBook10pt November 20, 2007

142 CHAPTER 3

Lyapunov function candid ate V (x

, x

) =

(α

+ α

), where

, α

> 0. Now, the Lyapu nov d erivative is given by

V (x

, x

) = α

˙x

+ α

˙x

+ α

˙x

= x

(α

+ α

(3.14)

Since I

< 0 it follows that there exist α

, α

> 0 such that α

+ α

= 0. In this case,

V (x

, x

) = 0, and hence, the zero

solution to (3.11)–(3.13) is Lyapunov stable. S how that the zero solution to

(3.11)–(3.13) is Lyapunov stable without the constraint I

> I

> 0 so

long as I

, I

> 0. △

Example 3.2. Consider the nonlinear dynamical system describing the

motion of a simple pendulum with viscous damping given by

θ(t) +

sin θ(t) = 0, θ(0) = θ

θ(0) =

, t ≥ 0, (3.15)

where g is the acceleration due to gravity and l is the length of the pen dulum.

To analyze the stability of this s ystem consider the Lyapunov function

candidate

V (θ,

θ) =

(θ +

θ)

(1 − cos θ). (3.16)

Now, the L yapunov derivative is given by

V (θ,

θ) =

θ + (θ +

θ)(

θ +

θ) +

θ sin θ = −(

θ sin θ), (3.17)

which is locally negative deﬁnite, and hence, the s imple pendulum with

viscous damping is locally asymptotically stable. Show that the e ne rgy

Lyapunov function V (θ,

θ) =

(1 − cos θ) fails to show that the

Lyapunov derivative is strictly decreasing and, hence, cannot be used in

conjunction with Theorem 3.1 to establish asymptotic stability of (3.15).△

Theorem 3.1 can be used to provide an estimate of the domain of

attraction for the nonlinear dynamical system (3.1); th at is, ﬁnding an

open connected set D

in R

containing the origin with the property that

every trajectory starting in D

converges to the origin as time approaches

inﬁnity. It is important to note here that (3.3) and (3.5) are not suﬃcient to

guarantee that every solution th at starts in D will remain in D for all time.

However, if (3.3) and (3.5) hold, then every i nv ariant set of the nonlinear

dynamical system (3.1) contained in D is also contained in the domain of

attraction D

of (3.1). As shown in the proof of Theorem 3.1 if there exists

a Lyapunov function V : D → R such th at (3.2), (3.3), and (3.5) hold, and

if D

= {x ∈ D : V (x) ≤ β} is bounded, then D

is a positively invariant set

with respect to (3.1) and every system trajectory starting in D

converges

to the origin as time approaches inﬁnity. Hence, D

is an estimate of the

domain of attraction. The question is then how large can we take β > 0 such

that D

remains bound ed ? Since V (·) is continuous and positive deﬁnite,

there always exists a small enough β > 0 such that the Lyapunov level

surface V (x) ≡ β is bounded, and hence, D

is bounded since D

⊂ B

(0)

NonlinearBook10pt November 20, 2007

STABILITY THEORY FOR NONLINEAR SYSTEMS 143

for some ε > 0. However, depending on the structure of V (·), as β in creases

the Lyapunov level surface V (x) = β can be unbounded, and hence, D

becomes unbounded. For D

⊂ B

(0), β must satisfy β < inf

kxk≥ε

V (x).

Hence, if β < γ, where

γ = lim

ε→∞

inf

kxk≥ε

V (x) < ∞ (3.18)

and γ > 0, then D

is guaranteed to be bound ed .

Next, we give a precise deﬁnition for the domain, or region, of

attraction of the zero solution x(t) ≡ 0 of the nonlinear dynamical system

(3.1).

Deﬁnition 3.2. Suppose the zero solution x(t) ≡ 0 to (3.1) is

asymptotically stable. Then the domain of attraction D

⊆ D of (3.1) is

given by

△

= {x

∈ D : if x(0) = x

, then lim

t→∞

x(t) = 0}. (3.19)

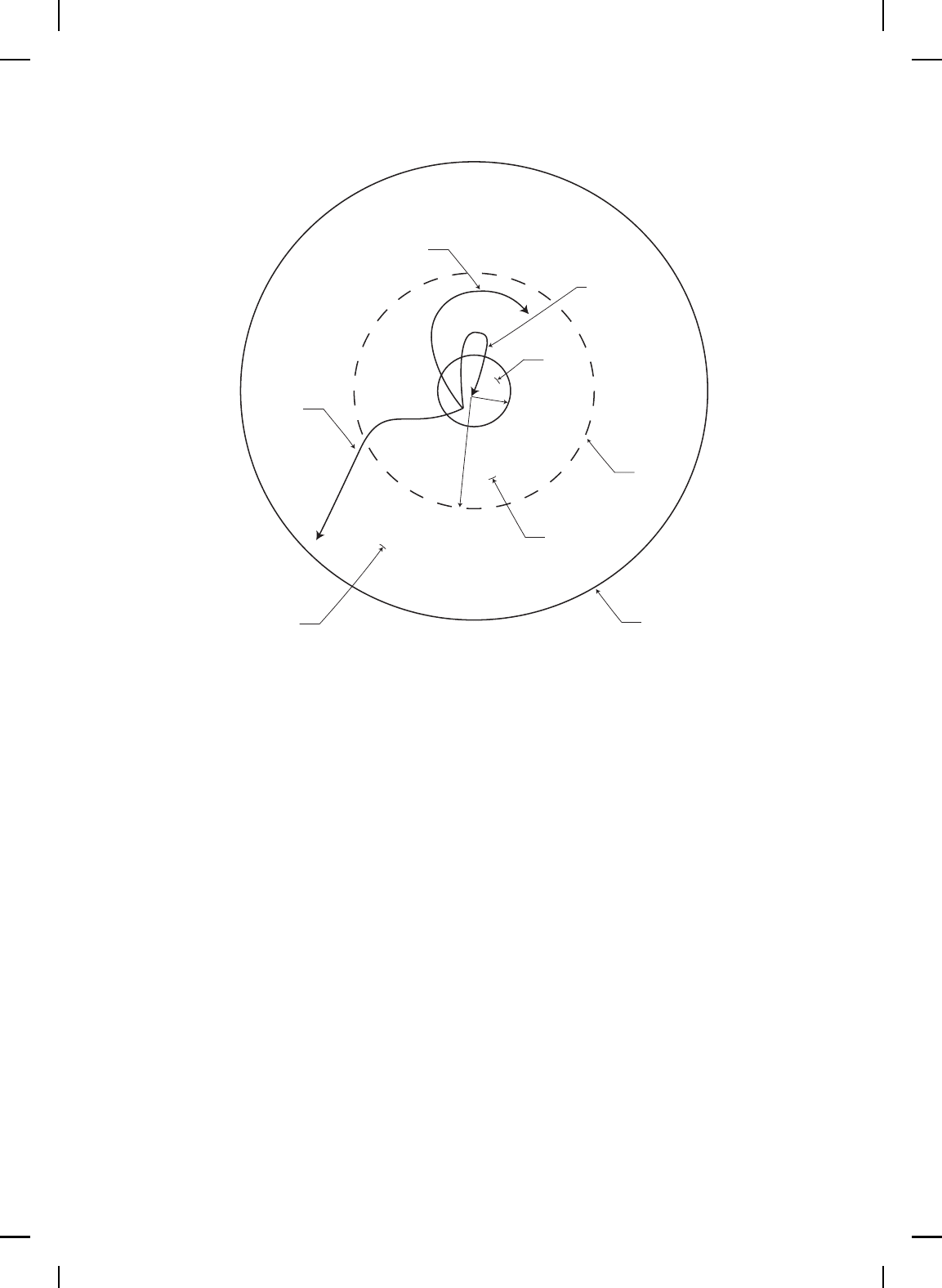
As discussed above, the motivation for constructing the domain of

attraction of a nonlinear dynamical system follows from the fact that there

is no guarantee that a system trajectory starting in a subset D of the state

space will remain in D even though the Lyapunov derivative is negative

in D, that is, the system trajectories move from one energy level to an

inner energy level (see Figure 3.6). The problem of constructing the domain

of attraction for locally stable nonlinear dyn amical systems has received

considerable attention in the literature [102, 174, 178, 285, 314, 443, 481].

Since, however, constructing the actual domain of attraction of a nonlinear

dynamical system is system trajectory d ependent, most of the techniques

proposed in th e literature p rovide a guaranteed sub s et of the domain of

attraction.

To estimate a subset of the domain of attraction of the dynamical

system (3.1) assume there exists a continuously diﬀerentiable f unction V :

D → R such that (3.2), (3.3), and (3.5) are satisﬁed. Next, let D

be the

connected component of {x ∈ D : V (x) ≤ β} containing the origin. Note

that every trajectory starting in D

will move to an inner energy surface

and, hence, cannot escape D

. Hence, D

is an estimate of the domain of

attraction of the nonlinear dynamical system (3.1). Now, to maximize this

estimate of the d omain of attraction we maximize β such that D

⊆ D.

Hence, deﬁne V

△

= sup{β > 0 : D

⊆ D} so that

△

= {x ∈ D : V (x) ≤ V

}, (3.20)

is a subset of the domain of attraction for (3.1) since

V (x) < 0 for all

x ∈ D

\ {0} ⊆ D \ {0}.

NonlinearBook10pt November 20, 2007

144 CHAPTER 3

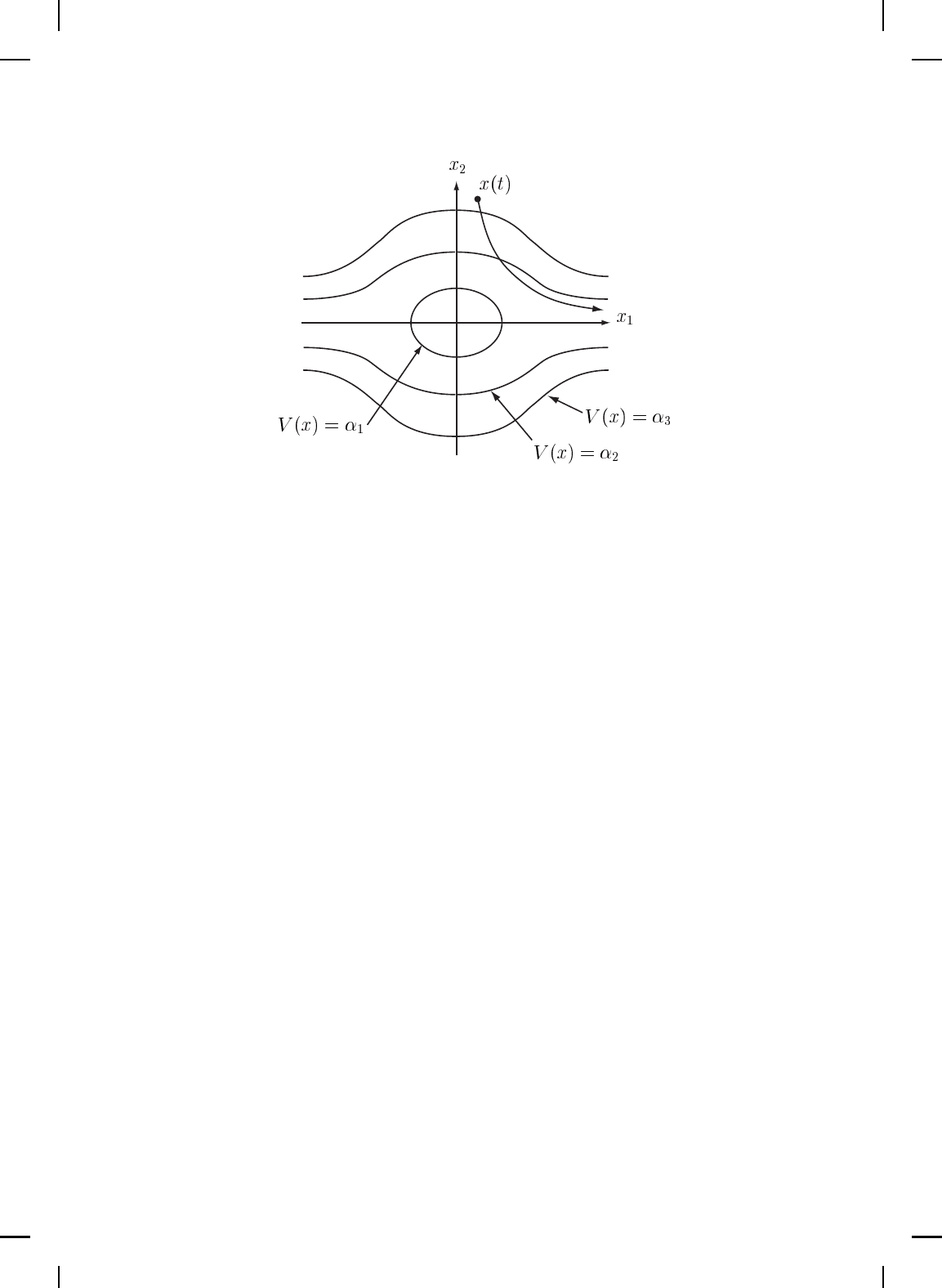
Figure 3.6 Visualization of the radial unbound edness req uirement; α

< α

The above discussion raises an interesting question; namely, under

what conditions will the d omain of attraction correspond to the entire state

space R

? Of course, this corresponds to the case where the trajectory

s(t, x

) of (3.1) approaches the origin as t → ∞ for all x

∈ R

or,

equivalently, the dynamical system is globally asymptotically stable. It

follows f rom the proof of Theorem 3.1 th at global asymptotic stability w ill

hold if every point x ∈ R

is contained in the compact set D

for some

β > 0. Clearly, in this case we require D = R

and that for every β > 0, D

is bounded, that is, for every β > 0 there exists r > 0 such that if x ∈ D

then x ∈ B

(0) or, equivalently, V (x) > β for all x 6∈ B

(0). This condition

ensuring that D

is bounded for all β > 0 is implied by

V (x) → ∞ as kxk → ∞. (3.21)

A fun ction V (·) satisfying (3.21) is called proper or radially unbounded.

Next, we state the global Lyapunov stability theorem wh ere the

domain of attraction of (3.1) is the entire state s pace.

Theorem 3.2. Consider the nonlinear dynamical system (3.1) and

assume there exists a continuously diﬀerentiable function V : R

→ R s uch

that

V (0) = 0, (3.22)

V (x) > 0, x ∈ R

, x 6= 0, (3.23)

′

(x)f(x) < 0, x ∈ R

, x 6= 0, (3.24)

V (x) → ∞ as kxk → ∞. (3.25)