Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

STABILITY THEORY FOR NONLINEAR SYSTEMS 145

Then the zero solution x(t) ≡ 0 to (3.1) is globally asymptotically stable. If,

alternatively, there exist scalars α, β, ε > 0, and p ≥ 1, such that V : R

→ R

satisﬁes

αkxk

≤ V (x) ≤ βkxk

, x ∈ R

(3.26)

′

(x)f(x) ≤ −εV (x), x ∈ R

, (3.27)

then the zero solution x(t) ≡ 0 to (3.1) is globally exponentially stable.

Proof. Let x(0) ∈ R

, and let β

△

= V (x

). Now, the radial

unboundedness condition (3.25) implies th at there exists ε > 0 such that

V (x) > β for all x ∈ R

such that kxk ≥ ε. Hence, it f ollows from (3.24)

that V (x(t)) ≤ V (x

) = β, t ≥ 0, which implies that x(t) ∈ B

(0), t ≥ 0.

Now, the proof follows as in the p roof of Theorem 3.1.

The following example adopted from [178] shows the motivation for

the radial unboundedness condition in ensuring global asymptotic stability.

Example 3.3. Consider the nonlinear d ynamical system

˙x

(t) = −

(t)

[1 + x

(t)]

+ 2x

(t), x

(0) = x

, t ≥ 0, (3.28)

˙x

(t) = −

2[x

(t) + x

(t)]

[1 + x

(t)]

, x

(0) = x

. (3.29)

To examine the stability of th is system, consider the Lyapunov function

candidate V (x

, x

) = x

/(1 + x

) + x

. Note that V (0, 0) = 0 and

V (x

, x

) > 0, (x

, x

) ∈ R × R, (x

, x

) 6= (0, 0); however, V (x

, x

) is

not radially unbounded. The Lyapunov derivative

V (x

, x

) is given by

V (x

, x

) =



(1 + x

) − 2x

(1 + x

)



˙x

+ 2x

˙x

(1 + x

)



−

(1 + x

)

+ 2x



−

+ x

)

(1 + x

)

= −

12x

(1 + x

)

−

(1 + x

)

< 0, (x

, x

) ∈ R × R, (x

, x

) 6= (0, 0). (3.30)

Clearly, th e Lyapunov derivative is negative deﬁnite in all of R

and hence, the zero solution (x

(t), x

(t)) ≡ (0, 0) to (3.28) and (3.29)

is asymptotically stable. However, to show that (3.28) and (3.29) is not

globally asymptotically stable, consider the hyperbola x

= 2/(x

−

√

2) in

NonlinearBook10pt November 20, 2007

146 CHAPTER 3

the x

-x

plane. Now, on the hyperbola, ˙x

/ ˙x

is given by

˙x



−

√

−2(x

+ x

)

−6x

+ 2x

(1 + x

)



−

√

= −

+ 2

√

+ 1

(3.31)

whereas the slope of the hyperbola is given by

= −

−

√

= −

−

√

+ 1

. (3.32)

Next, for x

√

2, it follows from (3.31) and (3.32) that

+ 2

√

+ 1 >

−

√

+ 1,

and h en ce,

˙x



−

√

, (3.33)

for x

√

2. Furthermore, note that for x

√

˙x

−

√

= −

(1 + x

)

−

√

4 + 6

√

+ 2x

+ 4x

(1 + x

)

−

√

> 0. (3.34)

Since on the hyperbola ˙x

> 0 for x

√

2, it follows that the

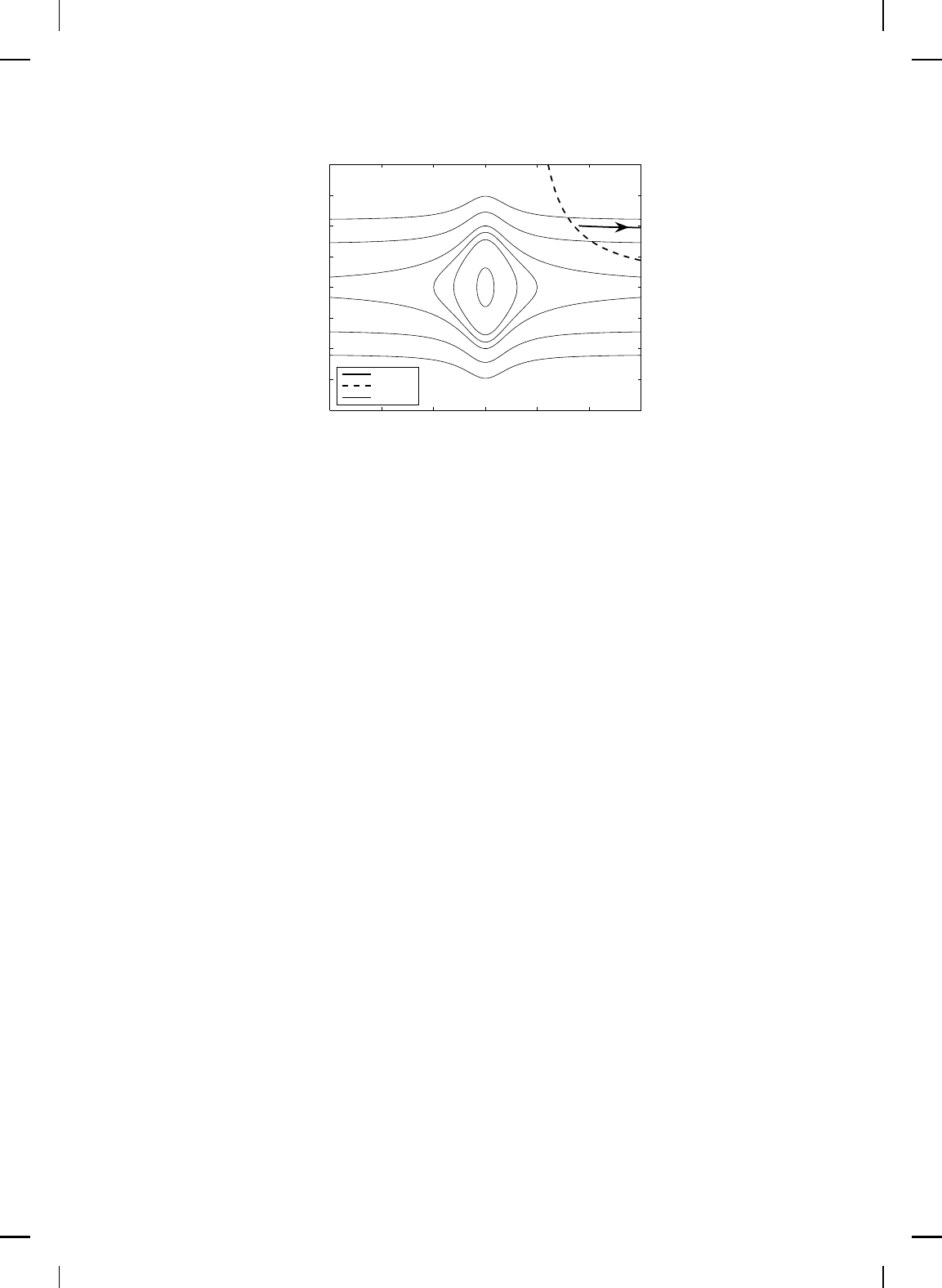
trajectories of (3.28) and (3.29) cannot cut the b ranch of the hyperbola

lying in the ﬁrst quadrant in the x

-x

plane, and in the direction toward

the x

-x

axes (see Figure 3.7). Hence, since trajectories starting to the right

of the hyperbola cannot reach the origin, it follows that the zero solution

(t), x

(t)) ≡ (0, 0) to (3.28) and (3.29) is not globally asymptotically

stable. △

The radial unboundedness condition (3.25) ensures that the constant

energy surfaces V (x) = α, α > 0, are hypersurfaces, and hence, since the

system trajectories move from one energy surface to an inner energy surface,

the system trajectories cannot d rift away from the system equilibrium.

Example 3.4. Consider the nonlinear d y namical system

˙x

(t) = −x

(t) + x

(t), x

(0) = x

, t ≥ 0, (3.35)

˙x

(t) = −x

(t) −x

(t), x

(0) = x

. (3.36)

To examine the stability of this system, consider the Lyapunov function

candidate V (x

, x

) =

, w hich is positive deﬁnite and radially

NonlinearBook10pt November 20, 2007

STABILITY THEORY FOR NONLINEAR SYSTEMS 147

−6 −4 −2 0 2 4 6

−2

−1.5

−1

−0.5

0.5

1.5

trajectory

hyperbola

level sets

Figure 3.7 Level sets and an unbounded trajectory for Example 3.3.

unbounded in R

. Now, the Lyapunov derivative is given by

V (x

, x

) = x

˙x

+ x

˙x

= −x

− x

< 0, (x

, x

) 6= (0, 0), (3.37)

which implies that the zero solution (x

(t), x

(t)) ≡ (0, 0) to (3.35) and

(3.36) is globally asymp totically stable. Is this system globally exponentially

stable? △

3.3 Invariant Set Stability Theorems

In this section, we introduce the Barbashin-Krasovskii-LaSalle invariance

principle to relax on e of the cond itions on the Lyapunov f unction V (·) in the

theorems given in Section 3.2. In particular, the strict negative-deﬁniteness

condition on the Lyapunov derivative can be relaxed while ensuring system

asymptotic stability. Speciﬁcally, if a continuously diﬀerentiable function

deﬁned on a compact invariant set with respect to the nonlinear dynamical

system (3.1) can be constructed whose derivative along the system’s

trajectories is negative semideﬁnite and no system traj ectories can stay

indeﬁnitely at points where the function’s derivative vanishes, then the

system’s equilibrium point is asymptotically stable. This result follows

from the Barbashin-Krasovskii-LaSalle invariance principle for nonlinear

dynamical systems, which we now state and prove.

Theorem 3.3 (Barbashin-Krasovskii-LaSalle Theorem). Consider the

nonlinear dynamical system (3.1), assume that D

⊂ D is a compact

positively invariant set with respect to (3.1), and assume there exists a

continuously diﬀerentiable function V : D

→ R such that V

′

(x)f(x) ≤

0, x ∈ D

. Let R

△

= {x ∈ D

: V

′

(x)f(x) = 0} and let M be the largest

invariant set contained in R. If x(0) ∈ D

, then x(t) → M as t → ∞.

NonlinearBook10pt November 20, 2007

148 CHAPTER 3

Proof. Let x(t), t ≥ 0, be a solution to (3.1) with x(0) ∈ D

. Since

′

(x)f(x) ≤ 0, x ∈ D

, it follows that

V (x(t)) − V (x(τ)) =

′

(x(s))f(x(s))ds ≤ 0, t ≥ τ,

and h en ce, V (x(t)) ≤ V (x(τ)), t ≥ τ, which implies that V (x(t)) is a

nonincreasing function of t. Next, since V (·) is continuous on the compact

set D

, there exists β ∈ R such that V (x) ≥ β, x ∈ D

. Hence,

△

= lim

t→∞

V (x(t)) exists. Now, for all p ∈ ω(x

) there exists an

increasing unbounded sequence {t

}

∞

n=0

, with t

= 0, such that x(t

) → p

as n → ∞. Since V (x), x ∈ D

, is continuous, V (p) = V (lim

n→∞

x(t

)) =

lim

n→∞

V (x(t

)) = γ

, and hence, V (x) = γ

on ω(x

). Now, since D

is compact and positively invariant it follows that x(t), t ≥ 0, is bounded,

and hence, it follows from Theorem 2.41 that ω(x

) is a nonempty, compact

invariant set. Hence, it follows that V

′

(x)f(x) = 0 on ω(x

) and thus

ω(x

) ⊂ M ⊂ R ⊂ D

. Finally, since x(t) → ω(x

) as t → ∞, it f ollows

that x(t) → M as t → ∞.

The construction of V (·) in Theorem 3.3 can be used to guarantee

the existence of the compact positively invariant s et D

. Speciﬁcally, if

= {x ∈ D : V (x) ≤ β}, where β > 0, is bounded and

V (x) ≤ 0,

x ∈ D

, then we can always take D

= D

. As discussed in Section 3.1,

if V (·) is positive deﬁnite, then D

is bounded for suﬃciently small β > 0.

Alternatively, if V (·) is radially unbounded, then D

is bounded for every

β > 0 irrespective of whether V (·) is positive deﬁnite or not.

Example 3. 5. The Barbashin-Krasovskii-LaSalle invariant set theo-

rem can be used to examine th e stability of limit cycles. To see this, consider

the nonlinear dynamical system

˙x

(t) = 4x

(t)x

(t) − g

(t))[x

(t) + 2x

(t) −4], x

(0) = x

, t ≥ 0,

(3.38)

˙x

(t) = −2x

(t) −g

(t))[x

(t) + 2x

(t) − 4], x

(0) = x

, (3.39)

where x

) > 0, x

6= 0, x

) > 0, x

6= 0, g

(0) = 0, and g

(0) = 0.

Now, note th at the s et deﬁned by the ellipse E

△

= {(x

, x

) ∈ R × R :

+ 2x

− 4 = 0} is invariant since

(t) + 2x

(t) −4] = −[2x

(t)g

(t)) + 4x

(t)g

(t))]

·[x

(t) + 2x

(t) −4]

= 0, t ≥ 0, (3.40)

and hence, if (x

(0), x

(0)) ∈ E, th en (x

(t), x

(t)) ∈ E, t ≥ 0. The motion

NonlinearBook10pt November 20, 2007

STABILITY THEORY FOR NONLINEAR SYSTEMS 149

on E is characterized by either of the equations

˙x

(t) = 4x

(t)x

(t), (3.41)

˙x

(t) = −2x

(t), (3.42)

which shows that E is a limit cycle for (3.38) and (3.39) where the state

vector moves clockwise.

To examine whether this limit cycle is attractive, deﬁne the function

V : R

→ R rep resenting a measure of the distance to the limit cycle by

V (x

, x

) = (x

+ 2x

−4)

and note that V (0, 0) = 16. Next, let β > 0 and

deﬁne

△

= {(x

, x

) ∈ R ×R : V (x

, x

) ≤ β}

= {(x

, x

) ∈ R ×R : (x

+ 2x

− 4)

≤ β}. (3.43)

Now, note that

V (x

, x

) = 2(x

+ 2x

− 4)

+ 2x

− 4)

= −2(x

+ 2x

− 4)

[2x

) + 4x

)]

≤ 0, (x

, x

) ∈ D

. (3.44)

Next, deﬁning R

△

= {(x

, x

) ∈ R × R :

V (x

, x

) = 0} it follows that

the largest invariant set M ⊆ R is given by

M = {(0, 0)} ∪ {(x

, x

) ∈ R ×R : x

+ 2x

− 4 = 0}. (3.45)

Hence, it follows from Th eorem 3.3 that all system trajectories starting

in D

go to (0, 0) or E. However, for β < 16, since V (0, 0) = 16 an d

V (1, 0) = 9 < 16, it follows that (0, 0) 6∈ D

and (0, 0) corresponds to a

local maximum of V (x

, x

). Hence, (0, 0) is unstable. (Can this result

be obtained by Lyapunov’s indirect method? See T heorem 3.19.) Thus, if

(0), x

(0)) ∈ D

, then (x

(t), x

(t)) → E as t → ∞, establishing that the

limit cycle characterized by E is attractive. △

Next, using Theorem 3.3 we provide a generalization of Theorem 3.1

for local asymptotic s tability of a nonlinear dynamical s y stem.

Corollary 3.1. Consider the nonlinear dynamical system (3.1), assume

that D

⊂ D is a compact positively invariant set with respect to (3.1)

such that 0 ∈

◦

, and assume that there exists a continuously diﬀerentiable

function V : D

→ R such that V (0) = 0, V (x) > 0, x 6= 0, and V

′

(x)f(x) ≤

0, x ∈ D

. Furthermore, assume th at the set R

△

= {x ∈ D

: V

′

(x)f(x) = 0}

contains no invariant set other than the set {0}. Then the zero solution

x(t) ≡ 0 to (3.1) is asymptotically stable and D

is a su bset of the domain

NonlinearBook10pt November 20, 2007

150 CHAPTER 3

of attraction of (3.1).

Proof. Lyapunov stability of the zero solution x(t) ≡ 0 to (3.1) follows

from Theorem 3.1 since V

′

(x)f(x) ≤ 0, x ∈ D

. Now, it follows from

Theorem 3.3 that if x

∈ D

, then ω(x

) ⊆ M, where M denotes the

largest invariant set contained in R, which implies th at M = {0}. Hence,

x(t) → M = {0} as t → ∞, establishing asymptotic stability of the zero

solution x(t) ≡ 0 to (3.1).

Example 3.6. To see the utility of Corollary 3.1, consider the nonlinear

dynamical system d escribing the notion of a simple pendulum given in

Example 3.2. To examine the stability of this system consider the more

natural energy Lyapunov function candidate given by

V (θ,

θ) =

(1 − cos θ), (3.46)

with Lyapunov derivative

V (θ,

θ) =

θ +

θ sin θ = −

≤ 0, (θ,

θ) ∈ R ×R, (3.47)

establishing Lyapun ov stability of the zero solution (θ(t),

θ(t)) ≡ (0, 0).

Next, let β > 0 be such that D

△

= {(θ,

θ) : V (θ,

θ) ≤ β} is compact. Note

that D

is positively invariant. Now, to show asymptotic stability for this

system let R

△

= {(θ,

θ) ∈ R × R :

V (θ,

θ) = 0} = {(θ,

θ) ∈ R × R :

θ = 0}

and note th at

V (θ,

θ) < 0 everywhere except on the line

θ = 0, where

V (θ,

θ) = 0. Now, let M be the largest invariant set contained in R and note

that (0, 0) ∈ M ⊂ R since (0, 0) is an equilibrium point. Furthermore, note

that for the system to guarantee the condition

V (θ,

θ) = 0, the trajectory of

the system mus t lie on the line

θ = 0. Since

θ(t) ≡ 0 implies

θ(t) ≡ 0 which,

using (3.15), further implies sin θ(t) ≡ 0, it follows that, for θ ∈ (−π, π),

M = {(0, 0)} is the largest invariant set contained in R, and h en ce, by

Corollary 3.1, (θ(t),

θ(t)) → (0, 0) as t → ∞, establishing local asymptotic

stability. △

Example 3.7. Corollary 3.1 can also be used to characterize the

domain of attraction of a nonlinear dynamical system. To see this, consider

the nonlinear dynamical system

˙x

(t) = x

(t)[x

(t) + x

(t) − 1] − x

(t), x

(0) = x

, t ≥ 0, (3.48)

˙x

(t) = x

(t) + x

(t)[x

(t) + x

(t) − 1], x

(0) = x

, (3.49)

with Lyapunov function candidate V (x

, x

) = x

+ x

. Now, the Lyapu nov

derivative is given by

V (x

, x

) = 2x

˙x

+ 2x

˙x

= 2(x

+ x

)(x

+ x

− 1), (3.50)

which is strictly negative if 0 < x

+ x

< 1. Next, deﬁne D

△

= {(x

, x

) ∈

R × R : x

+ x

≤ β}, where β ∈ (0, 1), and note that R

△

= {(x

, x

) ∈

NonlinearBook10pt November 20, 2007

STABILITY THEORY FOR NONLINEAR SYSTEMS 151

V (x

, x

) = 0} = {(0, 0)} = M. Now, it follows from C orollary 3.1

that the zero solution (x

(t), x

(t)) ≡ (0, 0) to (3.48) and (3.49) is locally

asymptotically stable w ith D

being a subs et of the domain of attraction for

every β ∈ (0, 1). Hence, D

△

= {(x

, x

) ∈ R × R : x

+ x

< 1} is contained

in the domain of attraction of (3.48) and (3.49). △

In Theorem 3.3 and Corollary 3.1 we explicitly assumed that there

exists a compact invariant set D

⊂ D of (3.1). Next, we provide a result

that does not require the explicit assumption of the existence of a compact

invariant D

Theorem 3.4. Consider the nonlinear dynamical system (3.1) and

assume that there exists a continuously diﬀerentiable fu nction V : R

→ R

such that

V (0) = 0, (3.51)

V (x) > 0, x ∈ R

, x 6= 0, (3.52)

′

(x)f(x) ≤ 0, x ∈ R

. (3.53)

Let R

△

= {x ∈ R

: V

′

(x)f(x) = 0} and let M be the largest invariant set

contained in R. Then all solutions x(t), t ≥ 0, of (3.1) that are bounded

approach M as t → ∞.

Proof. Let x ∈ R

be such that trajectory s(t, x), t ≥ 0, of (3.1) is

bounded. Now, with D

= O

, it follows from Theorem 3.3 that s(t, x) →

M as t → ∞.

Next, we present the global invariant set theorem for guaranteeing

global asymptotic stability of a nonlinear dynamical system.

Theorem 3.5. Consider the nonlinear dynamical system (3.1) and

assume there exists a continuously diﬀerentiable function V : R

→ R s uch

that

V (0) = 0, (3.54)

V (x) > 0, x ∈ R

, x 6= 0, (3.55)

′

(x)f(x) ≤ 0, x ∈ R

, (3.56)

V (x) → ∞ as kxk → ∞. (3.57)

Furth ermore, assume that the set R

△

= {x ∈ R

: V

′

(x)f(x) = 0} contains

no invariant set other than the set {0}. Then the zero solution x(t) ≡ 0 to

(3.1) is globally asymp totically stable.

Proof. Since (3.54)–(3.56) h old, it follows from Theorem 3.1 th at

the zero solution x(t) ≡ 0 to (3.1) is Lyapunov stable while the radial

NonlinearBook10pt November 20, 2007

152 CHAPTER 3

unboundedness condition (3.57) implies that all solutions to (3.1) are

bounded. Now, Theorem 3.4 implies that x(t) → M as t → ∞. However,

since R contains no invariant set other than the set {0}, the set M is {0},

and h en ce, global asymptotic stability is immediate.

Theorems 3.3, 3.4, and 3.5 are known as invariant set theorems.

Since for local asymptotic s tability V (x) is deﬁned on a compact positively

invariant set D

, D

provides an estimate of the domain of attraction for the

nonlinear dynamical system (3.1) which is not necessarily of the form given

by (3.20). Finally, un like Lyapunov’s theorem, the Barbashin-Krasovskii-

LaSalle invariant set theorem relaxes the strict negative-deﬁniteness condi-

tion on the Lyapunov derivative

V (x), x ∈ D

, for both lo cal and global

asymptotic stability.

3.4 Construction of Lyapunov Functions

As shown in Sections 3.2 and 3.3 the key requirement in applying Lyapunov’s

direct method and the Barbashin-Krasovskii-LaSalle invariance principle

for examining the stability of nonlinear systems is the construction of a

Lyapunov function. For certain systems, especially on es that have physical

energy interpretations, constructing a sys tem Lyapunov function can be

straightforward. In other cases, however, that can be a diﬃcult task. In this

section, we pr esent four systematic approaches for constructing Lyapunov

functions; namely, th e variable gradient, Krasovskii’s, Zubov’s, and the

Energy-Casimir methods.

The variable gradient method assumes a certain form for the gradient

of an unknown Lyapunov function and then by integrating the assumed

gradient one can often arrive at a Lyapunov function. To see this, let V :

D → R be a continuously diﬀerentiable function and let g(x) =



∂V

∂x



Now, the derivative of V (x) along the trajectories of (3.1) is given by

V (x) =

i=1

∂V

∂x

˙x

i=1

∂V

∂x

(x)

∂V

∂x

∂V

∂x

, . . . ,

∂V

∂x







(x)







∂V

∂x

f(x)

NonlinearBook10pt November 20, 2007

STABILITY THEORY FOR NONLINEAR SYSTEMS 153

= g

(x)f(x). (3.58)

Next, construct g(x) such that g(x) is a gradient for a positive-deﬁnite

function and

V (x) = g

(x)f(x) < 0, x ∈ D, x 6= 0. Speciﬁcally, it follows

from (3.58) that the fu nction V (x) can be computed from the line integral

V (x) =

(s)ds =

i=1

(s)ds

. (3.59)

Recall that the line integral of a gradient vector g : R

→ R

is path

independ ent [12, Theorem 10-37], and hence, the integration in (3.59) can

be taken along any path joining the origin to x ∈ R

. Choosing a path made

up of line segments parallel to the coordinate axes, (3.59) becomes

V (x) =

, 0, . . . , 0)ds

, s

, . . . , 0)ds

+ ··· +

, x

, . . . , x

n−1

, s

)ds

. (3.60)

Alternatively, us ing the transform ation s = σx, where σ ∈ [0, 1], (3.59) can

be rewritten as

V (x) =

(σx)xdσ =

i=1

(σx)x

dσ. (3.61)

The following result shows that g(x) is a gradient of a real-valued

function V : R

→ R if and only if th e Jacobian matrix ∂g/∂x is symmetric.

Proposition 3.1. The function g : R

→ R

is the gradient vector of

a scalar-valued function V : R

→ R if and only if

∂g

∂x

∂g

∂x

, i, j = 1, . . . , n. (3.62)

Proof. If g

(x) =

∂V

∂x

, then g

(x) =

∂V

∂x

. Since

∂g

∂x

∂

∂x

∂g

∂x

i, j = 1, . . . , n, necessity is immediate. To show suﬃciency, assume

∂g

∂x

∂g

∂x

, i, j = 1, . . . , n, and deﬁne V (x) as the line integral

V (x) =

(σx)xdσ =

j=1

(σx)x

dσ. (3.63)

Hence,

∂V

∂x

j=1

∂g

∂x

(σx)x

σdσ +

(σx)dσ

NonlinearBook10pt November 20, 2007

154 CHAPTER 3

j=1

∂g

∂x

(σx)x

σdσ +

(σx)dσ

d(σg

(σx))

dσ

= g

(x), i = 1, . . . , n, (3.64)

which implies that g

(x) =

∂V

∂x

Choosing g(x) such that g

(x)f(x) < 0, x ∈ D, x 6= 0, it f ollows from

Proposition 3.1 that V (x) can be computed from the line integral

V (x) =

(σx)xdσ =

j=1

(σx)x

dσ. (3.65)

Once arriving at V (x), x ∈ D, it is important to check whether V (·) is

positive deﬁnite.

Example 3.8. Consider the nonlinear d y namical system

˙x

(t) = x

(t), x

(0) = x

, t ≥ 0, (3.66)

˙x

(t) = −[x

(t) + x

(t)] − sin(x

(t) + x

(t)), x

(0) = x

. (3.67)

To construct a Lyapunov function for (3.66) an d (3.67) let g(x) = [a

, a

+ a

]

and let a

= a

= β so that the symmetry

requirement (3.62) holds. Now,

V (x) = g

(x)f(x)

= (a

+ βx

−(βx

+ a

)[(x

+ x

) + sin(x

+ x

)]. (3.68)

Taking a

= 2β, a

= β, and β > 0 it follows that

V (x) = −βx

− β(x

+ x

) sin(x

+ x

) < 0, (x

, x

) ∈ D, (3.69)

where D

△

= {(x

, x

) : |x

+ x

| < π}. Hence,

V (x) =

(σx

, σx

+ g

(σx

, σx

]dσ

β[2x

+ 2x

+ x

]σdσ

= βx

+ βx

βx

. (3.70)

Note that V (0, 0) = 0 and V (x

, x

) =

βx

β(x

+ x

)

> 0, (x

, x

) ∈

R ×R, (x

, x

) 6= (0, 0), and hence, V (x), x ∈ D, is a Lyapunov function for

(3.66) and (3.67). △

Next, we present Krasovskii’s method for constructing a Lyapunov

function for a given nonlinear system. First, however, the following