Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 95

i) (Continuity): s(t, t

, ·) is continuous and s(·, t

, x

) is continuously

diﬀerentiable in t for all x

∈ D and t, t

∈ R.

ii) (Con s istency): For every x

∈ D and t

∈ R, s(t

, t

, x

) = x

iii) (Group property): s(t

, t

, x

) = s(t

, t

, s(t

, t

, x

)) for all t

, t

∈

R and x

∈ D.

As for the time-invariant case, we denote the time-varying dynamical

system (D, R, s) by G. Note th at if for every t

, t ∈ R such that t ≥ t

, and

τ ∈ R, x

∈ D, s(t + τ, t

+ τ, x

) = s(t, t

, x

), then the fu nction s(·, ·, ·)

remains unchanged under time translation. Hence, without loss of generality

we can set t

= 0. In this case, Deﬁnition 2.48 collapses to Deﬁnition 2.47

with s(t, 0, x

) = s(t, x

). As in the time-invariant case, since a time-varying

dynamical system involves the function s(·, ·, ·) describing the motion of

x ∈ D for all t ∈ R, it generates a time-varying diﬀerential equation on D.

In particular, the f unction f : R ×D → R

given by

f(t, x)

△

= lim

τ→t

t − τ

[s(t, t

, x) −s(τ, t

, x)] (2.211)

deﬁnes a continuous vector ﬁeld on D. Hence, the dynamical system G

deﬁned by Deﬁnition 2.48 gives rise to the time-varying diﬀerential equation

˙x(t) = f (t, x(t)), x(t

) = x

, t ∈ I

. (2.212)

Existence and uniqueness of solutions, extendability of solutions, and

continuous dependence on initial conditions and system parameter theorems

can now be developed for (2.212) as in the case for time-invariant systems.

To see that these results will not signiﬁcantly diﬀer fr om the results already

developed note that by deﬁning x

(τ)

△

= x(t) and x

(τ)

△

= t, where τ = t−t

the solution x(t), t ∈ I

, to the nonlinear time-varying dynamical system

(2.212) can be equivalently characterized by the solution x

(τ), τ ∈ I

to the nonlinear time-invariant system

˙x

(τ) = f(x

(τ), x

(τ)), x

(0) = x

, τ ∈ I

, (2.213)

˙x

(τ) = 1, x

(0) = t

, (2.214)

where ˙x

(·) and ˙x

(·) in (2.213) and (2.214) denote diﬀerentiation with

respect to τ . Next, we state the key results on the existence and

uniqueness of solutions for time-varying dynamical systems needed for later

developments. The pr oofs of these results are similar to the proofs given in

earlier sections and are left as exercises for the reader.

Theorem 2.37. Consider the nonlinear dynamical system (2.212).

Assume f(t, ·) : D → R

is continuous on D for all t ∈ [t

, t

] and f(·, x) :

, t

] → R

is piecewise continuous on [t

, t

] for all x ∈ D. Then for every

NonlinearBook10pt November 20, 2007

96 CHAPTER 2

∈ D there exists τ > t

such that (2.212) has a piecewise continuously

diﬀerentiable solution x : [t

, τ] → R

. Furthermore, if f (·, x) : [t

, t

] → R

is continuous on [t

, t

] for all x ∈ D, then x : [t

, τ] → R

is continuously

diﬀerentiable on [t

, τ].

Theorem 2.38. Consider the nonlinear dynamical system (2.212).

Assume f (t, ·) : D → R

is Lipschitz continuous on D for all t ∈ [t

, t

]

and f(·, x) : [t

, t

] → R

is piecewise continuous on [t

, t

] for all x ∈ D.

Then, for every x

∈ D, there exists τ ∈ (t

, t

) such that (2.212) has a

unique solution x : [t

, τ] → R

over the interval [t

, τ].

Theorem 2.39. Consider the nonlinear dynamical system (2.212).

Assume f (t, ·) : D → R

is Lipschitz continuous on D for all t ∈ [t

, t

]

and f(·, x) : [t

, t

] → R

is piecewise continuous on [t

, t

] for all x ∈ D.

Furth ermore, let D

⊂ D be compact and suppose for x

∈ D

every solution

x : [t

, τ] → D lies entirely in D

. Then there exists a unique solution

x : [t

, ∞) → R

to (2.212) for all t ≥ t

Theorem 2.40. Consider the nonlinear dynamical system (2.212).

Assume f (t, ·) : D → R

is Lipschitz continuous on D for all t ∈ [t

, t

]

and f(·, x) : [t

, t

] → R

is piecewise continuous on [t

, t

] for all x ∈ D. In

addition, assume there exists α = α(x

) such that max

t∈R

kf(t, x

)k ≤ α.

Then, for all x

∈ R

, (2.212) has a unique solution x : (−∞, ∞) → R

over

all t ∈ R.

If we assume that f (t, 0) = 0, t ∈ R, then the assumption kf(t, x

)k ≤

α in Theorem 2.40 follows as a direct consequence of Lipschitz continuity

condition on f(t, ·) : D → R

and, hence, is automatic. To see this, note

that in this case Lipschitz continuity implies that kf(t, x

)k ≤ Lkx

k. In

this book we will assume that f(·, ·) has at least one equilibrium point in D

so that, without loss of generality, f (t, 0) = 0, t ∈ R. However, as seen in

Example 2.2, there are systems that have no equilibrium points. For these

systems, the assumption kf(t, x

)k ≤ α in Theorem 2.40 is necessary.

2.12 Limit Points, Limit Sets, and Attractors

In this section, we introduce the notion of invariance with respect to the ﬂow

) of a nonlinear dynamical system. Consider the nonlinear dynamical

system

˙x(t) = f (x(t)), x(0) = x

, t ∈ R, (2.215)

where x(t) ∈ D, t ∈ R, D is an open subset of R

, and f : D → R

Lipschitz continuous on D. Recall that (2.215) deﬁnes a dynamical system

in the sense of Deﬁnition 2.47 with ﬂow s : R × D → D. In addition, recall

that for x ∈ D, the map s(·, x) : R → D deﬁnes the solution curve or

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 97

trajectory of (2.215) through the point x in D. Identifying s(·, x) with its

graph, the trajectory or orbit of a point x

∈ D is deﬁned as the motion

along the curve

△

= {x ∈ D : x = s(t, x

), t ∈ R}. (2.216)

For t ≥ 0, we deﬁne the positive orbit throu gh the point x

∈ D as the

motion along the curve

△

= {x ∈ D : x = s(t, x

), t ≥ 0}. (2.217)

Similarly, the negative orbit through the point x

∈ D is deﬁned as

−

△

= {x ∈ D : x = s(t, x

), t ≤ 0}. (2.218)

Hence, th e orbit O

of a point x ∈ D is given by O

∪ O

−

= {s(t, x) : t ≥

0} ∪ {s(t, x) : t ≤ 0}.

Deﬁnition 2.49. A point p ∈ D is a positive limit point of the

trajectory s(·, x) of (2.215) if there exists a m on otonic sequence {t

}

∞

n=0

of positive numbers, with t

→ ∞ as n → ∞, such that s(t

, x) → p as

n → ∞. A point q ∈ D is a negative limit point of the trajectory s(·, x) of

(2.215) if there exists a monotonic sequence {t

}

∞

n=0

of negative numbers,

with t

→ −∞ as n → ∞, such that s(t

, x) → q as n → ∞. The set of all

positive limit points of s(t, x), t ≥ 0, is the positive limit set ω(x) of s(·, x) of

(2.215). The set of all negative limit points of s(t, x), t ≤ 0, is the negative

limit set α(x) of s(·, x) of (2.215).

An equivalent deﬁnition of ω(x

) and α(x

) which is geometrically

easier to see is ω(x

) = ∩

t≥0

and α(x

) = ∩

t≤0

−

(see Problem 2.114).

In the literature, the positive limit set is often referred to as the ω-limit set

while the negative limit set is referred to as th e α-limit set. Note that if

p ∈ D is a positive limit point of the trajectory s(·, x), then for all ε > 0

and ﬁnite time T > 0 there exists t > T such that kx(t) − pk < ε. This

follows from the fact that kx(t) −pk < ε for all ε > 0 and some t > T > 0 is

equivalent to the existence of a sequence {t

}

∞

n=0

, with t

→ ∞ as n → ∞,

such that x(t

) → p as n → ∞. An analogous observation holds for negative

limit points.

Deﬁnition 2.50. A set M ⊂ D ⊆ R

is a positively invariant set

with respect to the nonlinear d y namical system (2.215) if s

(M) ⊆ M for

all t ≥ 0, where s

(M)

△

= {s

(x) : x ∈ M}. A set M ⊂ D ⊆ R

a negatively invariant set with respect to the nonlinear dynamical system

(2.215) if s

(M) ⊆ M f or all t ≤ 0. A set M ⊆ D is an invariant set with

respect to the dynamical system (2.215) if s

(M) = M for all t ∈ R.

In the case wh ere t ≥ 0 in (2.215), note that a set M ⊆ D is a

NonlinearBook10pt November 20, 2007

98 CHAPTER 2

negatively invariant set with respect to the nonlinear dynamical system

(2.215) if, for every y ∈ M and every t ≥ 0, there exists x ∈ M such

that s(t, x) = y and s(τ, x) ∈ M for all τ ∈ [0, t]. Hence, if M is negatively

invariant, then M ⊆ s

(M) for all t ≥ 0; the converse, however, is not

generally true. Furthermore, a set M ⊂ D is an invariant set with respect

to (2.215) (deﬁned over t ≥ 0) if s

(M) = M for all t ≥ 0. Note that a set

M is invariant if and only if M is positively and negatively invariant.

The following propositions give several properties of positively invari-

ant, negatively invariant, and invariant sets.

Proposition 2.31. Consider the nonlinear d ynamical system G given

by (2.215). Let {M

: i ∈ I} be a collection of positively invariant

(respectively, negatively invariant or invariant) sets with respect to G. T hen

M =

i∈I

and N =

i∈I

are positively invariant (respectively,

negatively invariant or invariant) sets with respect to G.

Proof. Let the sets M

be positively invariant. For every x ∈ N,

it follows that x ∈ M

for some i ∈ I. Since M

is positively invariant,

s(t, x) ∈ M

for all t ≥ 0. Thus, since M

⊆ N, s(t, x) ∈ N for all t ≥ 0,

and hence, N is positively invariant. Next, let x ∈ M. I n this case, x ∈ M

for every i ∈ I and since each M

is positively invariant, s(t, x) ∈ M

for

each i ∈ I and each t ≥ 0. Hence, s(t, x) ∈

i∈I

= M for each t ≥ 0,

which proves positive invariance of M. The proofs for negative invariance

and invariance are analogous and are left as exercises for the reader.

Proposition 2.32. Consider the nonlinear d ynamical system G given

by (2.215). Let M ⊂ D be a positively invariant (respectively, negatively

invariant or invariant) set with respect to G. Then M is positively invariant

(respectively, negatively invariant or invariant) with respect to G.

Proof. Let M be invariant and let x ∈ M and t ∈ R. In this case,

there exists a sequence {x

}

∞

n=0

⊆ M such that x

→ x as n → ∞. Since M

is invariant, s(t, x

) ∈ M for each n. Furthermore, since s(t, x

) → s(t, x)

as n → ∞ it follows that s(t, x) ∈ M, and hence, M is invariant. The proofs

of positive and negative invariance are identical and, hence, are omitted.

Proposition 2.33. Consider the nonlinear d ynamical system G given

by (2.215). Then M ⊂ D is positively invariant with respect to G if and

only if D \ M is negatively invariant with respect to G. Furthermore, M is

invariant with respect to G if and only if D \M is invariant w ith respect to

Proof. Let M be positively invariant and suppose, ad absurdum, that

if x ∈ D \M and t ≤ 0, then s(t, x) 6∈ D \M. Hence, s(t, x) ∈ M and since

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 99

−t ≥ 0, s(−t, s(t, x)) = s(−t+t, x) = s(0, x) = x ∈ M by positive invariance

of M. This contradiction shows that D \ M is negatively invariant. The

converse statement follows by retracing the steps above. Finally, the second

part of the theorem follows as a direct consequence from the ﬁrst part.

Proposition 2.34. Consider the nonlinear d ynamical system G given

by (2.215). Let M ⊂ D be invariant with respect to G. Then ∂M and

◦

are invariant with respect to G.

Proof. It follows from Proposition 2.33 that if M is invariant with

respect to G, then D \ M is invariant with respect to G. Hence, by

Proposition 2.32, M and D \M are invariant with respect to G. Now,

it follows from Pr opositions 2.31 and 2.33 that ∂M = M ∩ (D \ M) and

◦

M= D \ (D \ M) are invariant with respect to G.

The converse of Proposition 2.34 holds whenever M is open or closed.

To see this, note that if ∂M is invariant with respect to G, then

◦

M is

invariant with respect to G. This simple fact can be shown by a contradiction

argument. Speciﬁcally, suppose, ad absurdum, that there exist x ∈

◦

M and

t ∈ R such th at s(t, x) 6∈

◦

M. Now, since the set Q

△

= {y ∈ D : y = s(t, x), t ∈

[0, τ]} is connected it follows that Q ∩ ∂M 6= Ø, where we have assumed

t ≥ 0 for convenience. Hence, there exists t

∗

∈ (0, t] such that s(t

∗

, x) ∈ ∂M.

However, in this case, x = s(−t

∗

, s(t

∗

, x)) = s(−t

∗

+ t

∗

, x) ∈ ∂M, which by

invariance of ∂M contradicts x ∈

◦

M. This shows that if ∂M is invariant

with respect to G, then

◦

M is invariant with respect to G. Thus, if M is

closed then M = ∂M∪

◦

M is invariant, whereas if M is open then M =

◦

is invariant. Similarly, it can be shown that if

◦

M is nonempty and invariant,

then M is also invariant whenever M is closed or open.

Proposition 2.35. Consider the nonlinear d ynamical system G given

by (2.215). Let M ⊂ D be positively (respectively, negatively) invariant

with respect to G. Then

◦

M is positively (respectively, negatively) invariant

with respect to G.

Proof. Assume M is positively invariant. Then by Propositions 2.32

and 2.33 D \ M and D \ M are negatively invariant. Hence,

◦

M= D \

(D \ M) is positively invariant. The case where M is n egatively invariant

follows using identical arguments.

Deﬁnition 2.51. The trajectory s(·, x) of (2.215) is bounded if there

NonlinearBook10pt November 20, 2007

100 CHAPTER 2

exists γ > 0 such that ks(t, x)k < γ, t ∈ R.

Next, we state and prove a key theorem involving positive limit sets.

An analogous result holds for negative limit sets an d is left as an exercise

for the reader (see Problem 2.113). In the case where t ≥ 0, we refer to the

group property in Deﬁnition 2.47 as the semigroup property. Furthermore,

we use the notation x(t) → M ⊆ D as t → ∞ to denote that x(t) approaches

M, that is, for each ε > 0 there exists T > 0 such that dist(x(t), M) < ε

for all t > T , where dist(p, M)

△

= inf

x∈M

kp −xk.

Theorem 2.41. Suppose the solution x(t) to (2.215) correspond ing

to an initial condition x(0) = x

is bounded for all t ≥ 0. Then the

positive limit set ω(x

) of x(t), t ≥ 0, is a nonempty, compact, invariant,

and connected set. Fur thermore, x(t) → ω(x

) as t → ∞.

Proof. Let x(t), t ≥ 0, or, equivalently, s(t, x

), t ≥ 0, denote

the solution to (2.215) corresponding to the initial condition x(0) = x

Next, since x(t) is bounded for all t ≥ 0, it follows from the Bolzano-

Weierstrass theorem (Theorem 2.3) that every sequ en ce in the positive orbit

△

= {s(t, x) : t ∈ [0, ∞)} has at least one accumulation point p ∈ D as

t → ∞, and hence, ω(x

) is nonempty. Next, let p ∈ ω(x

) so that there

exists an increasing unbounded sequence {t

}

∞

n=0

, with t

= 0, such that

lim

n→∞

x(t

) = p. Now, since x(t

) is uniformly bounded in n it follows that

the limit point p is bounded, which implies that ω(x

) is bounded. To show

that ω(x

) is closed let {p

}

∞

i=0

be a sequence contained in ω(x

) such that

lim

i→∞

= p. Now, since p

→ p as i → ∞ for every ε > 0, there exists an i

such that kp−p

k < ε/2. Next, since p

∈ ω(x

), there exists t ≥ T , where T

is arbitrary and ﬁn ite, such that kp

−x(t)k < ε/2. Now, since kp−p

k < ε/2

and kp

−x(t)k < ε/2 it follows that kp −x(t)k ≤ kp

−x(t)k+ kp −p

k < ε,

and hence, p ∈ ω(x

). Thus, every accumulation point of ω(x

) is an element

of ω(x

) so that ω(x

) is closed. Hence, since ω(x

) is closed and bounded

it is compact.

To show positive invariance of ω(x

) let p ∈ ω(x

) so that th ere

exists an increasing unbounded sequence {t

}

∞

n=0

such that x(t

) → p

as n → ∞. Now, let s(t

, x

) denote the solution x(t

) of (2.215) with

initial condition x(0) = x

and note that since f : D → R

in (2.215) is

Lipschitz continuous on D, x(t), t ≥ 0, is the unique solution to (2.215) so

that by the semigroup property s(t + t

, x

) = s(t, s(t

, x

)) = s(t, x(t

)).

Now, since x(t), t ≥ 0, is continuous it follows that, for t + t

≥ 0,

lim

n→∞

s(t + t

, x

) = lim

n→∞

s(t, x(t

)) = s(t, p), and hen ce, s(t, p) ∈

ω(x

). Hence, s

(ω(x

)) ⊆ ω(x

), t ≥ 0, establishing positive invariance of

ω(x

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 101

To show invariance of ω(x

) let y ∈ ω(x

) so that there exists an

increasing unbounded sequence {t

}

∞

n=0

such that s(t

, x

) → y as n → ∞.

Next, let t ∈ [0, ∞) and note that there exists N such that t

> t, n ≥

N. Hence, it follows from the semigroup property that s(t, s(t

− t, x

)) =

s(t

, x

) → y as n → ∞. Now, it follows from the Bolzano-Lebesgue theorem

(Theorem 2.4) that there exists a subsequence {z

}

∞

k=1

of the sequence

= s(t

−t, x

), n = N, N + 1, . . ., such that z

→ z ∈ D as k → ∞ and,

by deﬁnition, z ∈ ω(x

). Next, it follows from th e continuous dependence

property th at lim

k→∞

s(t, z

) = s(t, lim

k→∞

), and hence, y = s(t, z),

which implies th at ω(x

) ⊆ s

(ω(x

)), t ∈ [0, ∞). Now, using positive

invariance of ω(x

) it follows that s

(ω(x

)) = ω(x

), t ≥ 0, establishing

invariance of the positive limit set ω(x

To show connectedness of ω(x

), suppose, ad absurdum, th at ω(x

) is

not connected. In this case, there exist two nonempty closed sets P

and

such that P

∩ P

= Ø and ω(x

) = P

∪ P

. Since P

and P

are

closed and disjoint there exist two open sets S

and S

such that S

∩S

= Ø,

⊂ S

, and P

⊂ S

. Next, since f : D → R is Lipschitz continuous on D

it follows that the solution x(t), t ≥ 0, to (2.215) is a continuous fu nction of

t. Hence, there exist sequences {t

}

∞

n=0

and {τ

}

∞

n=0

such that x(t

) ∈ S

x(τ

) ∈ S

, and t

< τ

< t

n+1

, w hich implies that there exists a sequence

{τ

}

∞

n=0

, with t

< τ

n+1

, such that x(τ

) 6∈ S

∪S

. Next, since x(t) is

bounded for all t ≥ 0, it follows that x(τ

) → ˆp 6∈ ω(x

) as n → ∞, leading

to a contradiction. Hence, ω(x

) is connected.

Finally, to show x(t) → ω(x

) as t → ∞, suppose, ad absurdum,

x(t) 6→ ω(x

) as t → ∞. In this case, there exists a sequence {t

}

∞

n=0

, with

→ ∞ as n → ∞, such that

inf

p∈ω(x

)

kx(t

) − pk > ε, n ∈ Z

. (2.219)

However, since x(t), t ≥ 0, is bounded, the bounded sequence {x(t

)}

∞

n=0

contains a convergent subsequence {x(t

∗

)}

∞

n=0

such that x(t

∗

) → p

∗

∈ ω(x

)

as n → ∞, which contradicts (2.219). Hence, x(t) → ω(x

) as t → ∞.

It is important to note that Theorem 2.41 holds for time-invariant

nonlinear dynamical systems (2.215) possessing u nique solutions forward in

time with the solutions being continuous f unctions of the initial conditions.

More generally, letting s(·, x

) denote the solution of a d y namical system

with initial condition x(0) = x

, Theorem 2.41 holds if s(t + τ, x

) =

s(t, s(τ, x

)), t, τ ≥ 0, and s(·, x

) is a continuous function of x

∈

D. Of course, if f(·) is Lipschitz continuous on D then there exists a

unique solution to (2.215), and hence, the r equ ired semigroup property

s(t + τ, x

) = s(t, s(τ, x

)), t, τ ≥ 0, and the continuity of s(t, ·) on D,

t ≥ 0, hold. Alternatively, uniqueness of solutions in forward time along

NonlinearBook10pt November 20, 2007

102 CHAPTER 2

with the continuity of f(·) ensure that the solutions to (2.215) satisfy the

semigroup property and are continuous fu nctions of the initial conditions

∈ D even when f(·) is not Lipschitz continuous on D (see [96, Theorem

4.3, p. 59]). More generally, f (·) need not be continuous. In particular, if

f(·) is discontinuous bu t bounded and x(·) is the unique solution to (2.215)

in the sense of Filippov [118], then the required semigroup property along

with the continuous dependence of solutions on initial conditions hold [118].

Note that Theorem 2.41 implies that if p ∈ D is an ω-limit point of

a trajectory s(·, x) of (2.215), then all other points of the trajectory s(·, p)

of (2.215) through the point p are also ω-limit points of s(·, x), that is, if

p ∈ ω(x) th en O

⊂ ω(x). Furthermore, since every equilibrium point

∈ D of (2.215) satisﬁes s(t, x

) = x

for all t ∈ R, all equilibrium points

∈ D of (2.215) are th eir own α- and ω-limit sets. I f a traj ectory of

(2.215) possesses a unique ω-limit point x

, then it follows from Theorem

2.41 that since ω(x

) is invariant with respect to the ﬂow s

of (2.215), x

is an equilibrium point of (2.215).

Next, we establish an important property of limit sets with orbit

closures.

Theorem 2.42. Consider th e nonlinear dynamical system G given by

(2.215) and let O

and O

−

denote, respectively, the positive and n egative

orbits of G through the point x ∈ D. Then O

= O

∪ ω(x) and O

−

∪ α(x).

Proof. Recall that O

= {y ∈ D : y = s(t, x), t ≥ 0}. Now, it follows

from the deﬁnition of ω(x) that O

⊇ O

∪ ω(x). To show that O

⊆

∪ ω(x), let z ∈ O

. In this case, there exists a sequence {z

}

∞

n=0

⊆ O

such that z

→ z as n → ∞. Next, let z

= s(t

, x) for t

∈ R

. Now, either

there exists a subsequence {t

}

∞

k=0

such that t

→ ∞ as k → ∞, in which

case z ∈ ω(x), or since R

is closed it follows from the Bolzano-Lebesgue

theorem (Theorem 2.4) that there exists a subsequence {t

}

∞

k=0

such that

→ t ∈ R

. In the second case, s(t

, x) → s(t, x) ∈ O

as k → ∞,

and since s(t

, x) → z as k → ∞ it follows that z = s(t, x) ∈ O

. Hence,

⊆ O

∪ ω(x). The proof of O

−

= O

−

∪ α(x) follows using identical

arguments.

The next deﬁnition introduces the notions of attracting sets and

attractors. For this deﬁnition recall that a n eighborhood N of a set M ⊂ D

is deﬁn ed as N

△

= {x ∈ D : kx − yk < ε, y ∈ M} for some small ε > 0.

Deﬁnition 2.52. A closed invariant set M ⊂ D is an attracting set of

the dynamical s ys tem (2.215) if there exists a neighborhood N of M such

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 103

that, for all x ∈ N, s

(x) ∈ N for all t ≥ 0 and s

(x) → M as t → ∞.

A set M ⊂ D is an attractor of the dynamical s ystem (2.215) if M is an

attracting set of (2.215) and contains a dense orbit.

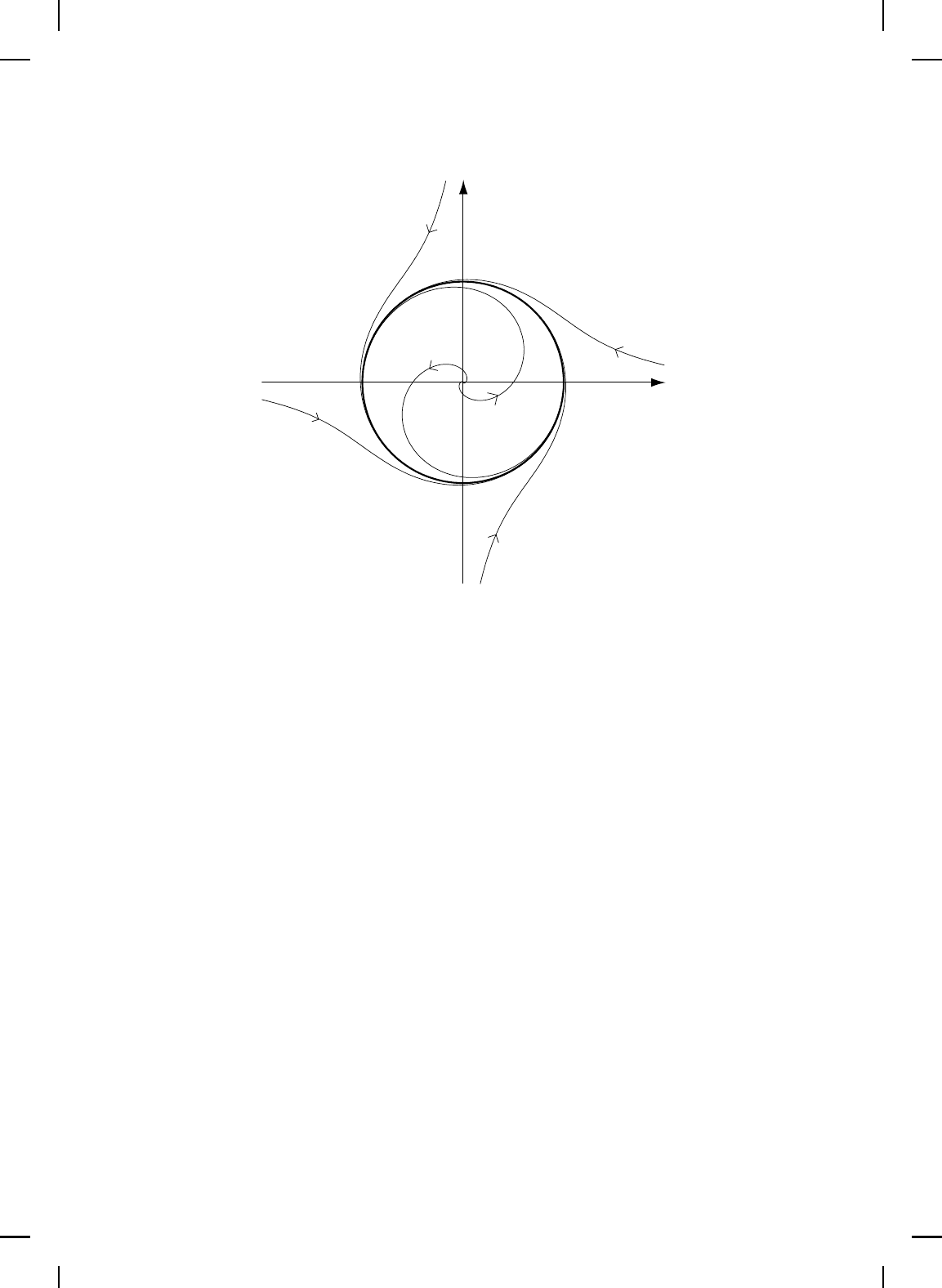
Example 2.38. Consider the nonlinear d ynamical system

˙x

(t) = −x

(t) + x

(t)[1 − x

(t) −x

(t)], x

(0) = x

, t ≥ 0, (2.220)

˙x

(t) = x

(t) + x

(t)[1 −x

(t) −x

(t)], x

(0) = x

. (2.221)

Rewriting (2.220) and (2.221) in terms of the polar coordinates r =

+ x

and θ = tan

−1

) as

˙r(t) = r(t)[1 − r

(t)], r(0) = r

△

+ x

, t ≥ 0, (2.222)

θ(t) = 1, θ(0) = θ

△

= tan

−1

), (2.223)

it can be shown that the set of equilibria f

−1

(0) consists of the origin x =

]

= 0. All solutions of the system starting from nonzero initial

conditions x(0) that are not on the un it circle C = {x ∈ R

: x

+ x

1} approach the unit circle. In particular, since ˙r > 0 for r ∈ (0, 1), all

solutions starting inside the unit circle spiral counterclockwise toward the

unit circle. Alternatively, since ˙r < 0 f or r > 1, all solutions starting outside

the unit circle spiral inward counterclockwise (see Figure 2.6). Hence, all

solutions to (2.220) and (2.221) are bounded and converge to C. Note that

the counterclockwise ﬂow on the unit circle characterizes a trajectory O

of (2.220) and (2.222) since ˙r = 0 on r = 1. Furthermore, O

is the ω-

limit set of every trajectory of (2.220) and (2.221) with the exception of the

equilibrium point x = 0. Clearly, O

is an attractor.

Since the vector ﬁeld (2.222) and (2.223) are Lipschitz continuous , the

solutions to (2.222) and (2.223) are unique and all solutions are deﬁned on R.

The system trajectories of (2.222) and (2.223) are shown in Figure 2.6 and

consist of i) an equilibrium point corresponding to the origin, ii) a perio dic

trajectory coinciding with the limit cycle C (see Deﬁnition 2.54), and iii)

spiraling trajectories passing through each point p = (r, θ) with r 6= 0 and

r 6= 1. For points p such that r ∈ (0, 1), ω(r, θ) = C and α(r, θ) = {0}.

For points p such that r > 1, ω(r, θ) = C and α(r, θ) = Ø. For points

p such that r = 1, ω(r, θ) = α(r, θ) = C. Hence, ω(r, θ) = C ∪ {0} and

α(r, θ) = C ∪ {0} ∪ Ø = C ∪ {0}, (r, θ) ∈ R × R. △

2.13 Periodic Orbits, Limit Cycles, and Poincar´e-

Bendixson Theorems

In this s ection we discuss periodic orbits and limit cycles. In particular, we

present several key techniques for predicting the existence of periodic orbits

NonlinearBook10pt November 20, 2007

104 CHAPTER 2

−1

Figure 2.6 Attractor for Example 2.38.

and limit cycles in nonlinear dynamical systems. Here we limit our attention

to planar (second-order) systems, whereas in Section 4.10 we address n-

dimensional periodic dynamical systems. Once again, we consider dynamical

systems of the form

˙x(t) = f (x(t)), x(0) = x

, t ∈ R, (2.224)

where x(t) ∈ D, t ∈ R, D is an open subset of R

, and f : D → R

Lipschitz continuous on D. The following deﬁnition introduces the notion

of periodic solutions and periodic orbits for (2.224).

Deﬁnition 2.53. A solution s(t, x

) of (2.224) is periodic if there exists

a ﬁnite time T > 0 such that s(t+T, x

) = s(t, x

) for all t ∈ R. The minimal

T for which the solution s(t, x

) of (2.224) is periodic is called the period. A

set O ⊂ D is a periodic orbit of (2.224) if O = {x ∈ D : x = s(t, x

), t ∈ R}

for some periodic solution s(t, x

) of (2.224).

Note that for every x ∈ D, s(t, x) has a period T = 0; however, s(t, x)

need not be periodic. Furtherm ore, if x

∈ D is an equilibrium point, then

every T ∈ R is a period of s(t, x

), and hence, s(t, x

) is periodic. Th e

next proposition gives a characterization of a periodic point of a n onlinear

dynamical system.