Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 75

i) Under what cond itions does (2.136) have at least one solution for a

given x

∈ D?

ii) Under what conditions does (2.136) have a unique solution for a given

∈ D?

iii) What is the maximal interval of existence over which one or more

solutions to (2.136) exist?

iv) What is the sensitivity of the solutions to (2.136) to initial data and/or

parameter perturbations?

Before addressing each of the above questions, we present a series of

examples that demonstrate the need for pr oviding conditions that guarantee

the existence and uniqueness of solutions to nonlinear diﬀerential equations.

Example 2.31. Consider the scalar non linear dynamical system

˙x(t) = −sign(x(t)), x(0) = 0, t ≥ 0, (2.138)

where

sign(x)

△



1, x ≥ 0,

−1, x < 0.

(2.139)

Now, note that since

(t) = − 2x(t)sign(x(t)) = −2|x(t)| ≤ 0, it f ollows

that x

(·) is a decreasing fu nction of time. Hence, if x(0) = 0, then x(t) = 0

for all t ≥ 0, which implies ˙x(t) = 0, t ≥ 0. In this case, sign(0) = 0,

which leads to a contradiction. Hence, there does not exist a continuously

diﬀerentiable function x(·) that satisﬁes (2.138). Note that the function

f(x) = −sign(x) is not continuous at x = 0. △

Example 2.32. Consider the scalar non linear dynamical system

˙x(t) = 3x

2/3

(t), x(0) = 0, t ≥ 0. (2.140)

This sys tem has two solutions given by x(t) = t

and x(t) = 0, t ≥ 0. Note

that the fu nction f(x) = 3x

2/3

is continuous at x = 0; however, it is not

Lipschitz continuous at x = 0. △

Example 2.33. Consider the scalar non linear dynamical system

˙x(t) = x

(t), x(0) = 1, t ≥ 0. (2.141)

Using separation of variables, the solution to (2.141) is given by

x(t) =

1 −t

. (2.142)

The solution (2.142) is deﬁned for t ∈ [0, 1) and becomes unbounded as

t → 1. The solution has a ﬁnite escape time and, hence, exists only locally

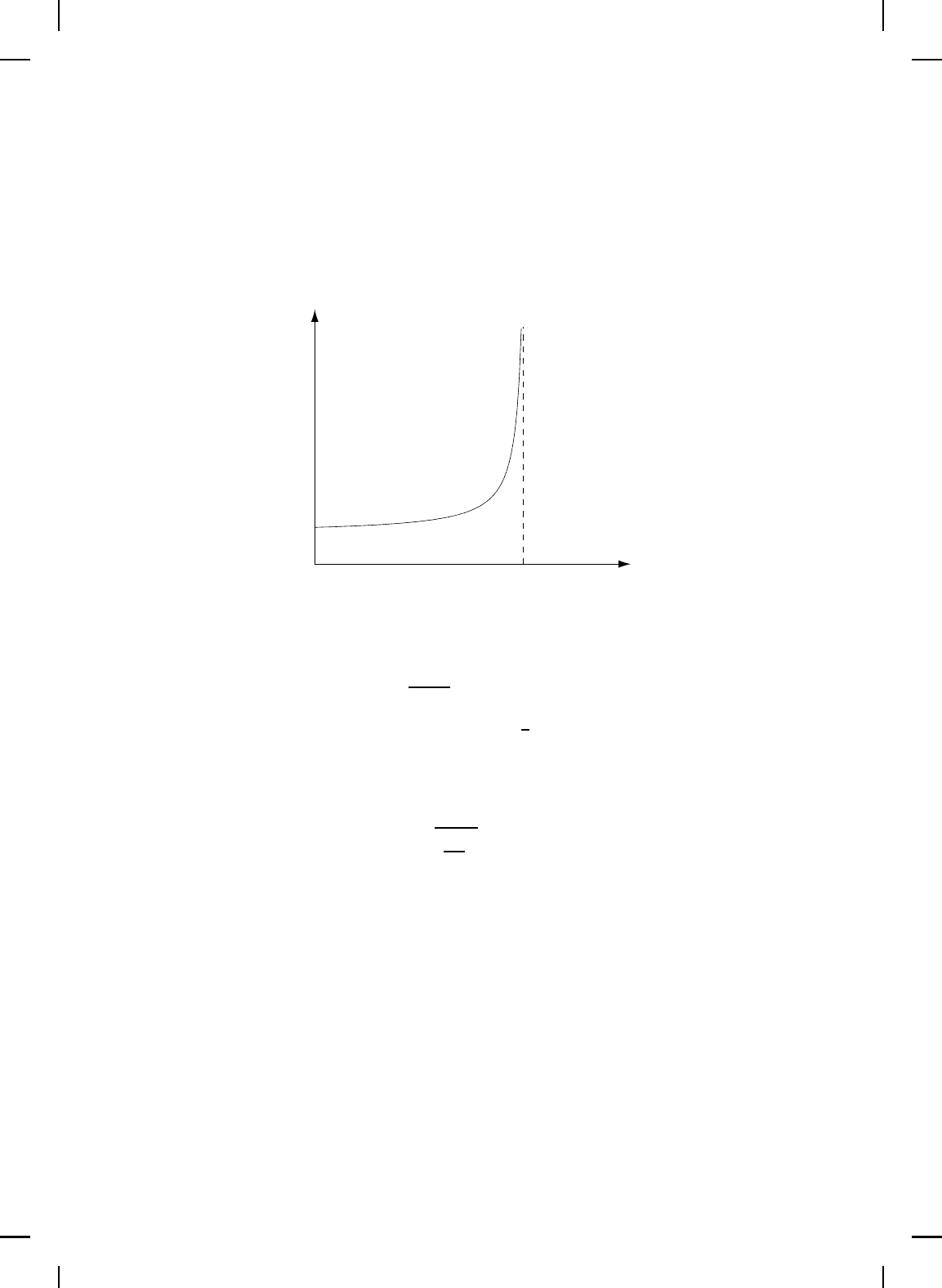
NonlinearBook10pt November 20, 2007

76 CHAPTER 2

(see Figure 2.4). Note that even though (2.142) has another branch deﬁned

on the interval (1, ∞), this branch is not considered part of the solution to

(2.141) since the initial time t

= 0 6∈ (1, ∞). Finally, note that f(x) = x

continuous and Lipschitz continuous at x = 0. However, f (x) is not globally

Lipschitz continuous on R. △

x(t)

0 1

Figure 2.4 Solution exhibiting ﬁnite escape time.

Example 2.34. Consider the scalar nonlinear dynamical system

˙x(t) =

|x(t)|, x(0) = 0, t ≥ 0. (2.143)

Clearly, x(t) = 0, t ≥ 0, as well as x(t) =

are solutions to (2.143). In

fact, th ere are in ﬁnitely many solutions to (2.143), parameterized by the

arbitrary time T , and are given by (see Figure 2.5)

x(t) =



0, 0 ≤ t ≤ T,

(t−T )

, t > T.

(2.144)

Note that the f unction f(x) =

|x| is continuous at x = 0; however, f(x)

is not Lipschitz continuous at x = 0. △

Examples 2.32–2.34 analyze nonlinear diﬀerential equations having

multiple solutions as well as ﬁnite escape time. However, th e nonlinear

diﬀerential equation in Example 2.31 does not have a solution in the sense

of the deﬁnition given in this section. The question of existence of solutions

is fundamental in the stud y of dynamical systems. The following result

provides a suﬃcient condition for the existence of solutions of (2.136) over

an interval [t

, τ] for suﬃciently small τ ∈ (t

, t

Theorem 2.24 (Peano). C on s ider the nonlinear dynamical system

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 77

x(t)

0 T 2T 3T

Figure 2.5 Multiple solutions.

(2.136). Assume f : D → R

is continuous on D. Then for every x

∈ D and

> 0 there exists τ > t

such that (2.136) has a continuously diﬀerentiable

solution x : [t

, τ] → R

Proof. L et η > 0 be such that B

) ⊆ D and let M

△

= sup{kf(x)k :

x ∈ B

)}. Now, let α, β > 0 be such that Mα ≤ β ≤ ε and let

△

= {x(·) ∈ C[t

, τ] : |||x − x

||| ≤ η, x(t

) = x

, t ∈ [t

, τ]},

where τ

△

= t

+ α. Note that S is convex, closed, and bounded. Next, let

P : C[t

, τ] → C[t

, τ] be given by

(P x)(t)

△

= x

f(x(s))ds, t ∈ [t

, τ]. (2.145)

Now, it follows that

k(P x)(t) −x

k =



f(x(s))ds



≤

kf(x(s))kdt

≤ M|t −t

≤ Mα

NonlinearBook10pt November 20, 2007

78 CHAPTER 2

≤ β, t ∈ [t

, τ],

which implies that P (S) is boun ded. Furthermore, since f is continuous on

D it follows that for every ε > 0, there exists δ > 0 such that

k(P x)(t) − (P ˆx)(t)k =



[f(x(s)) −f (ˆx(s))]ds



≤

kf(x(s)) −f (ˆx(s))kdt

≤ εα, t ∈ [t

, τ], sup

t∈[t

,τ]

kx(t) − ˆx(t)k < δ.

The result now is a dir ect consequence of the Schauder ﬁ xed point theorem

(see Problem 2.93) and the fact that x(t) = (P x)(t) is a s olution to (2.136)

if and only if x(t) is a ﬁxed point of P .

In order to guarantee the existence and uniqueness of solutions to

(2.136) we strengthen the hypothesis in Theorem 2.24. Speciﬁcally, we

assume that f is Lipschitz continuous on D. The following theorem gives

suﬃcient conditions for existence and uniqueness of solutions to (2.136). We

state the result for the right-hand limit; the result for the left-hand limit is

analogous.

Theorem 2.25. Consider the nonlinear dynamical system (2.136).

Assume that f : D → R

is L ipschitz continuous on D. Then, for all

∈ D, there exists τ ∈ (t

, t

) such that (2.136) has a unique solution

x : [t

, τ] → R

over the interval [t

, τ].

Proof. It f ollows from Theorem 2.24 that there exists τ > 0 and

x : [t

, τ] → R

such that x(·) is a continuous solution to (2.136). Now, let

(P x)(t)

△

= x

f(x(s))ds, t ∈ [t

, τ], (2.146)

so that x(t) = (P x)(t). Note that P : C[t

, τ] → C[t

, τ]. Furthermore, deﬁne

△

= {x(·) ∈ C[t

, τ] : |||x −x

||| ≤ r}, where r > 0 and x

: C[t

, τ] → C[t

, τ]

is such that x

(t) = x

for all t ∈ [t

, τ]. Note that x(·) is a s olution to

(2.136) over [t

, τ] if and only if (P x)(·) = x(·), that is, x(·) is a ﬁxed point

of P . Hence, us ing the fact that f : D → R

is Lipschitz continuous on D

and kx(t) − x

k ≤ r, t ∈ [t

, τ], it follows that, for each x(·) ∈ S and each

t ∈ [t

, τ],

k(P x)(t) − x

k =



f(x(s))ds



[f(x(s)) − f(x

) + f (x

)]ds



NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 79

≤

[kf(x(s)) − f (x

)k + kf(x

)k]ds

≤

[Lkx(s) − x

k+ α]ds

≤

(Lr + α)ds

= (t −t

)(Lr + α)

≤ (τ − t

)(Lr + α), (2.147)

where L > 0 is the Lipschitz constant of f with respect to x on B

) ⊂ D

and α = α(x

) = kf(x

)k, and hence,

|||P x − x

||| = max

t∈[t

,τ]

k(P x)(t) − x

k ≤ (τ − t

)(Lr + α). (2.148)

Now, choosing τ − t

≤

Lr+α

ensures that |||P x − x

||| ≤ r, and hence,

P : S → S.

To sh ow that P : S → S is a contraction, let x(·) and y(·) ∈ S so that

x(t), y(t) ∈ B

) for all t ∈ [t

, τ]. Hence,

(P x)(t) −(P y)(t) =

[f(x(s)) − f(y(s))]ds, (2.149)

which implies

k(P x)(t) −(P y)(t)k ≤

kf(x(s)) −f (y(s))kds

≤

Lkx(s) − y(s)kds

≤ L|||x −y|||

= L(t − t

)|||x − y|||

≤ ρ|||x −y|||,

where |||x − y||| = max

t∈[t

,τ]

kx(t) − y(t)k and L(t − t

) ≤ L(τ − t

) ≤ ρ.

Thus ,

|||P x − P y||| = max

t∈[t

,τ]

k(P x)(t) − (P y)(t)k ≤ ρ|||x − y|||. (2.150)

Now, choosing (τ − t

) ≤ ρ/L and ρ < 1 ensures that P : S → S is a

contraction. Hence, it follows from Theorem 2.22 th at for

τ − t

≤ min



− t

Lr + α



(2.136) has a unique solution in S.

NonlinearBook10pt November 20, 2007

80 CHAPTER 2

Finally, we show that P h as a u nique ﬁxed point in C[t, τ]. Suppose

x(·) ∈ C[t

, τ] satisﬁes (2.137). Then, x(0) = x

∈ B

). Now, since x(·)

is continuous, it follows for suﬃciently small t, x(t) ∈ B

). Suppose, ad

absurdum, that there exists ˆτ ∈ (t

, τ) such that x(ˆτ) 6∈ B

), that is,

kx(ˆτ ) − x

k > r. Since kx(t) − x

k is continuous in t and kx(0) − x

k = 0,

it follows that there exists τ

∗

< ˆτ < τ such that kx(t) − x

k < r for all

t ∈ [t

, τ

∗

) and kx(τ

∗

) − x

k = r. Now, for all t ≤ τ

∗

kx(t) − x

k =



f(x(s))ds



[f(x(s)) − f(x

) + f (x

)]ds



≤

Lkx(s) − x

kds + α(t − t

)

≤ (t − t

)(Lr + α)

≤ (τ

∗

− t

)(Lr + α). (2.151)

Since, t ≤ τ

∗

it follows th at r = kx(τ

∗

) − x

k ≤ (τ

∗

− t

)(Lr + α). Hence,

(τ

∗

−t

) ≥

Lr+α

≥ τ − t

, which is a contradiction. Hence, if x(·) ∈ C[t

, τ]

satisﬁes (2.136) s uch that τ − t

≤ min{t

− t

Lr+α

}, then x(·) ∈ S.

Thus , if x

∗

(·) is a ﬁxed point of C[t

, τ], then x

∗

∈ S, which shows that

(2.136) has a unique solution over the interval [t

, τ].

The following corollary to Theorem 2.25 is immediate.

Corollary 2.3. Consider the nonlinear dynamical system (2.136).

Assume that f : D → R

is continuously diﬀerentiable on D. Then, for

all x

∈ D, there exists τ ∈ (t

, t

) such that (2.136) has a unique solution

x : [t

, τ] → R

over the interval [t

, τ].

Proof. The proof follows by noting that continuous diﬀerentiability

on D implies Lipschitz continuity on D.

Next, we state and prove a very important theorem regarding the

sensitivity of solutions of (2.136) to the system initial data and system

parameters. For this result we require a key lemma due to Gronwall that

converts an implicit bound to an explicit bound.

Lemma 2.2 (Gronwall Lemma). Assume there exists a continuous

function x : R → R such that

x(t) ≤ α +

βx(s)ds, t ≥ t

, (2.152)

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 81

where α ∈ R and β ≥ 0. Then

x(t) ≤ αe

β(t−t

)

, t ≥ t

. (2.153)

Proof. Let α ∈ R and let

y(t) = α +

βx(s)ds, t ≥ t

. (2.154)

Now, it follows from (2.152) that x(t) ≤ y(t), t ≥ t

, and hence, using

(2.154),

˙y(t) = βx(t) ≤ βy(t), y(t

) = α, t ≥ t

. (2.155)

Next, deﬁne z(t)

△

= ˙y(t) − βy(t) and note that (2.155) implies z(t) ≤ 0,

t ≥ t

. Hence,

y(t) = y(t

β(t−t

)

β(t−σ)

z(σ)dσ,

which implies

y(t) ≤ y(t

β(t−t

)

= αe

β(t−t

)

, t ≥ t

The result is now immediate by noting that x(t) ≤ y(t), t ≥ t

Theorem 2.26. Consider the nonlinear dynamical system (2.136).

Assume that f : D → R

is uniformly Lipschitz continuous on D.

Furth ermore, let x(t) and y(t) be solutions to (2.136) with initial conditions

x(t

) = x

and y(t

) = y

over the closed interval [t

, t

]. Then, for

each ε > 0 and t ∈ [t

, t

], there exists δ = δ(ε, t − t

) > 0 such that if

− y

k < δ, then kx(t) − y(t)k ≤ ε.

Proof. Note that x(t) and y(t), t ∈ [t

, t

], satisfy

x(t) = x

f(x(s))ds, (2.156)

y(t) = y

f(y(s))ds. (2.157)

Subtracting (2.157) from (2.156) yields

x(t) − y(t) = x

− y

[f(x(s)) −f (y(s))]ds. (2.158)

Now, (2.158) implies

kx(t) − y(t)k ≤ kx

− y

kf(x(s)) −f (y(s))kds

≤ kx

− y

k+ L

kx(s) − y(s)kds, (2.159)

NonlinearBook10pt November 20, 2007

82 CHAPTER 2

where L > 0 is the Lipschitz constant of f. Using Lemma 2.2 it follows

that kx(t) − y(t)k ≤ kx

− y

L(t−t

)

, t ∈ [t

, t

]. Hence, for every ε > 0,

choosing δ = δ(ε, t − t

) =

L(t−t

)

yields the result.

Theorem 2.26 shows that the solution x(t), t ∈ [t

, t

], of (2.136)

depends continuously on the initial condition x(0) over a ﬁnite time interval.

This is not true in general over the semi-inﬁnite interval [t

, ∞). If th is

were the case over the semi-inﬁnite interval and δ(ε, t) could be chosen

independ ent of t, then continuous dependence of solutions uniformly in t

for all t ≥ 0 would imply Lyapunov stability of the solutions; a concept

introduced in Chapter 3. Furthermore, since Th eorem 2.26 imp lies

kx(t) − y(t)k ≤ kx

− y

L(t−t

)

, t ∈ [t

, t

], (2.160)

it follows that for each t ∈ [t

, t

lim

→x

s(t, y

) = s(t, x

). (2.161)

In addition, (2.160) implies that this limit is uniform for all t ∈ [t

, t

It is important to note that T heorem 2.26 also holds for the case where

f : D → R

is Lipschitz continuous on D. In this case, h owever, continuous

dependence on the initial conditions of s(t, y

) holds for s(·, ·) ∈ Q, where

Q = [t

, t

] × N

) and N

) ⊂ D. Finally, it is important to note

that Gronwall’s lemma can be used to give an alternative proof of Theorem

2.25. In particular, if, ad absurdum, we assume th at x(t) and y(t) are two

solutions to (2.136) with initial conditions x(t

) = x

and y(t

) = x

over

the closed interval [t

, t

], then it f ollows from (2.160) that kx(t)−y(t)k ≤ 0,

t ∈ [t

, t

]. This of cours e implies that x(t) = y(t), t ∈ [t

, t

], establishing

uniqueness of solutions.

The next result presents a m ore general version of Theorem 2.26 in-

volving continuous dependence on initial conditions and system parameters.

For this result, consider the nonlinear dynamical system

˙x(t) = f (x(t), λ), x(t

) = x

, t ∈ I

,λ

, (2.162)

where x(t) ∈ D, t ∈ I

,λ

, D is an open subset of R

, λ ∈ R

is a system

parameter vector, f : D × R

→ R

is such that f (·, λ) is Lipschitz

continuous on D, f(x, ·) is uniformly Lipschitz continuous on R

, and

,λ

= (τ

min

, τ

max

) ⊂ R is the maximal interval of existence for the solution

x(·) of (2.162).

Theorem 2.27. Consider the nonlinear dynamical system (2.162).

Assume that f : D × R

→ R

is such that for every λ ∈ R

, f(·, λ)

is Lipschitz continuous on D and for every x ∈ D, f(x, ·) is globally

Lipschitz continuous on R

. Furthermore, let x(t) and y(t) be solutions to

(2.162) with system parameters λ and µ, respectively, and initial conditions

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 83

x(t

) = x

and y(t

) = y

over the closed interval [t

, t

]. Then, for each

ε > 0 and t ∈ [t

, t

], there exists δ = δ(ε, t−t

) > 0 such that if kx

−y

k < δ

and kλ −µk < δ, then kx(t) −y(t)k ≤ ε.

Proof. The p roof is a direct consequence of Theorem 2.26 with x

x, y

, and y replaced by [x

]

, [x

]

, [y

]

, and [y

]

respectively.

As in the case of Theorem 2.26, Theorem 2.27 implies that

ks(t, x

, λ)−s(t, y

, µ)k ≤ (kx

−y

k+kλ−µk)e

L(t−t

)

, t ∈ [t

, t

], (2.163)

and h en ce,

lim

,µ)→(x

,λ)

s(t, y

, µ) = s(t, x

, λ), (2.164)

uniformly for all t ∈ [t

, t

Next, we present a diﬀerent kind of continuity of parameter result. In

particular, we show that given two dynamical systems

˙x(t) = f (x(t)), x(t

) = x

, t ∈ [t

, t

], (2.165)

˙y(t) = g(y(t)), y(t

) = y

, t ∈ [t

, t

], (2.166)

where f : D → R

and g : D → R

are both Lipschitz continuous on D,

and kf(x) − g(x)k ≤ ε, x ∈ D, the solutions to (2.165) and (2.166) with

− y

k ≤ γ remain nearby over a ﬁnite time interval.

Theorem 2.28. Consider the nonlinear dynamical system (2.165) and

(2.166). Ass ume that f : D → R

is uniformly Lipschitz continuous on D

with Lipschitz constant L and g : D → R

is Lips chitz continuous on D.

Furth ermore, suppose that

kf(x) −g(x)k ≤ ε, x ∈ D. (2.167)

If x(t) and y(t) are solutions to (2.165) and (2.166) on some time interval

I ⊂ R with kx

− y

k ≤ γ, then

kx(t) − y(t)k ≤ γe

L|t−t

− 1). (2.168)

Proof. For t ∈ I it follows that

x(t) −y(t) = x

− y

[f(x(s)) − g(y(s))]ds. (2.169)

Now, (2.169) implies

kx(t) −y(t)k ≤ kx

− y

k +

kf(x(s)) −g(y(s))kds

NonlinearBook10pt November 20, 2007

84 CHAPTER 2

≤ γ +

kf(x(s)) −f (y(s)) + f(y(s)) − g(y(s))kds

≤ γ +

kf(x(s)) −f (y(s))kds +

kf(y(s)) − g(y(s))kds

≤ γ +

Lkx(s) − y(s)kds +

εds, t ∈ I. (2.170)

Next, deﬁning q(t)

△

= kx(t) − y(t)k, (2.170) implies

q(t) ≤ γ + L

q(s) +

ds, t ∈ I, (2.171)

or, equivalently,

q(t) +

≤ γ +

+ L

q(s) +

ds, t ∈ I. (2.172)

Now, using Gronwall’s lemma it follows that

q(t) +

≤



+ γ



L|t−t

, t ∈ I, (2.173)

which implies (2.168).

Theorem 2.28 shows that, given two solutions to a dynamical system

with initial conditions that are close at the same value of time, these

solutions will remain close over the entire time interval I and n ot j ust at

the initial time. Furthermore, it is clear from (2.168) that bounds on the

initial condition errors and the solution errors grow exponentially in time,

with the Lipschitz constant L controlling the growth rate. In the study

of robustness, that is, sensitivity to system parameter variations, (2.168)

tells us that a solution to an approximate dynamical system will serve as

an approximate solution to the actual system over a ﬁnite time interval.

Furth ermore, (2.168) clearly shows why the qualitative study of diﬀerential

equations is necessary an d why numerical method s (which are approximate

by d eﬁ nition) are inherently fragile over long periods of time and can be

untru stworthy.

Finally, we close this section with a proposition th at shows that the

solution of a nonlinear system satisfying a uniform Lipschitz continuity

condition is exponentially bounded from above and below.

Proposition 2.30. Consider the nonlinear dynamical system (2.136).

Assume f : D → R

is uniformly Lipschitz continuous on D with Lipschitz

constant L and f (0) = 0. Then the solution x(t) of (2.136) over the closed

interval [t

, t

] satisﬁes

−L|t−t

≤ kx(t)k

≤ kx

L|t−t

, t ∈ [t

, t

]. (2.174)