Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 65

|||f |||

∞,q

△

= sup

t∈[0,∞)

kf(t)k

. (2.108)

Here, the vector norm (q part) is the spatial norm; the p part is the temporal

norm. Note that the norm ||| · |||

p,q

satisﬁes Axioms i) and iii) of Deﬁnition

2.39. However, since there exist many nonzero functions f : [0, ∞) → R

such that |||f |||

p,q

= 0, p ∈ [1, ∞), it f ollows that Axiom ii) of Deﬁnition 2.39

can be violated with the norm |||·|||

p,q

. Speciﬁcally, if f (·) is a fun ction such

that it is zero almost everywhere or, equivalently, f (·) is zero everyw here on

[0, ∞) except on a set of m easure zero [288], then f(·) satisﬁes |||f |||

p,q

= 0.

To address such functions the concepts of Lebesgue measure and measurable

spaces [288] can be used with the integral in (2.107) denoting the Lebesgue

integral. In this case, the function ||| · |||

p,q

is a valid norm on the s pace

of measurable fun ctions f : [0, ∞) → R

with the interpretation that if

|||f |||

p,q

= 0, then f (t) = 0 almost everywhere on [0, ∞). We denote this

normed linear space by L

or, equivalently, the set of measurable functions

such that |||f|||

p,q

< ∞, q ∈ [1, ∞], that is,

△

= {f : [0, ∞) → R

: f is measurable and |||f |||

p,q

< ∞, q ∈ [1, ∞]}.

In this case, |||f |||

∞,q

given by (2.108) is replaced by

|||f |||

∞,q

△

= ess sup

t∈[0,∞)

kf(t)k

, (2.109)

where “ess” denotes essential.

Example 2. 28. Let C[a, b] denote the set of continuous functions

mapping the bounded interval [a, b] into R

. Furthermore, for f, g ∈ C[a, b]

and α ∈ R, let (f + g)(t)

△

= f(t) + g(t) and (αf )(t) = αf(t). Now, deﬁne

the norm ||| · ||| : R

→ R by |||f |||

∞,q

= max

t∈[a,b]

kf(t)k

. Note that since

f is deﬁned on the bounded interval [a, b] and f is continuous, ||| · ||| is a

well-deﬁned norm and is ﬁnite f or every f (·) ∈ C[a, b]. Clearly, |||f|||

∞,q

≥ 0

and is zero only for f (t) ≡ 0. To show that Axioms iii) and iv) of Deﬁnition

2.39 hold note that for f(·), g(·) ∈ C[a, b] it follows that

|||f + g|||

∞,q

= max

t∈[a,b]

kf(t) + g(t)k

≤ max

t∈[a,b]

[kf(t)k

+ kg(t)k

]

= |||f|||

∞,q

+ |||g|||

∞,q

. (2.110)

Furth ermore,

|||αf |||

∞,q

= max

t∈[a,b]

kαf(t)k

= max

t∈[a,b]

|α|kf(t)k

= |α| max

t∈[a,b]

kf(t)k

NonlinearBook10pt November 20, 2007

66 CHAPTER 2

= |α||||f |||

∞,q

. (2.111)

Hence, C[a, b] endowed with th e n orm ||| · |||

∞,q

is a normed linear space. △

Note that in the above discussion we can also allow f : [0, ∞) → R

n×m

in a similar way where the spatial norm is a matrix norm. Furthermore, in

the matrix case, we can deﬁne induced norms for linear operators G : L

→

of the form y(t) = G[u](t). One such indu ced norm |||G|||

(q,s),(p,r)

is deﬁn ed

|||G|||

(q,s),(p,r)

△

= sup

|||u|||

p,r

|||G[u]|||

q,s

, (2.112)

which corresponds to an induced operator norm from an input signal u(t)

with p temporal norm and r spatial norm to an output signal y(t) with q

temporal norm and s spatial norm. For further details, see Chapter 7.

Some norm ed vector spaces are not large enough to permit limit

operations. In particular, if {f

}

∞

n=1

denotes a sequence of functions

belonging to a normed linear space such that lim

n→∞

|||f − f

||| = 0, then a

natural question is whether f is a member of the norm ed linear space. As an

example, consider the space of continuous functions on [0, 1] with the norm

deﬁned by |||f ||| =

|f(t)|dt. Now, consider the sequence of continuous

functions

(t) =



1 − nt, t ∈ [0, 1/n),

0, t > 1/n,

(2.113)

and d eﬁ ne f by

f(t) =



1, t = 0,

0, t > 0.

(2.114)

Then it can be easily seen th at lim

n→∞

|||f

− f||| = 0. However, the limit

f is not continuous, that is, f is not a member of the vector space. In

other words, our linear space was too small for the norm we deﬁn ed on it.

In order to address the above observations we introduce the concept of a

Cauchy sequence.

Deﬁnition 2.43. A sequence {x

}

∞

n=1

in a normed linear space is called

a Cauchy sequence if, for every ε > 0, th ere exists an integer N = N(ε) such

that |||x

− x

||| < ε, whenever n, m > N.

Note that an equivalent condition for a Cauchy sequence is lim

n,m→∞

|||x

− x

||| = 0. Thus, the main diﬀerence between a convergent sequence

and a C auchy sequence is that in the former case the terms in the sequence

approach a limit point, wh ereas in the latter case the terms in the sequence

approach each other. The following proposition shows that every convergent

sequence in a n ormed linear space is a Cauchy sequence.

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 67

Proposition 2.29. Assume that the sequence {x

}

∞

n=1

converges in a

normed linear space. Then for every ε > 0 there exists an integer N such

that |||x

− x

||| < ε whenever n > N and m > N .

Proof. Let x = lim

n→∞

. Given ε > 0, let N be such that |||x

−x||| <

ε/2, whenever n > N. Now, if m > N, then |||x

−x||| < ε/2. If n > N and

m > N it follows f rom the triangle inequ ality that

|||x

− x

||| = |||x

− x + x − x

||| ≤ |||x

− x||| + |||x − x

||| <

= ε.

Hence, {x

}

∞

n=1

is a Cauchy sequence.

Even though every convergent sequence is Cauchy, the converse is not

necessarily true in a normed linear space. In particular, if the elements of

a sequence get closer to each other, that does not imply that the sequence

is convergent. However, there exist normed linear s paces w here this is true.

These spaces are known as Banach spaces.

Deﬁnition 2.44. A n ormed linear space is called a complete space or

a Banach space if every Cauchy sequence converges to an element in the

space.

Example 2.29. Once again, we consider the set C[a, b] of continuous

functions mapping the boun ded interval [a, b] into R

addressed in Example

2.28. To show that C[a, b] is a Banach space let {f

}

∞

n=0

be a Cauchy

sequence in C[a, b]. Now, for every ﬁxed t ∈ [a, b],

(t) −f

(t)k

≤ |||f

− f

|||

∞,q

→ 0 as n, m → ∞, (2.115)

and hence the real vectors {f

(t)}

∞

n=0

form a Cauchy sequence in R

. Since

with k · k

, q ∈ [1, ∞], is a complete space [373] it follows that there

exists f (t) such that f

(t) → f(t) as n → ∞. To show that the sequence

}

∞

n=0

converges to f uniform ly in t, let ε > 0 and choose N such that

|||f

−f

|||

∞,q

< ε/2 for all n, m > N . Now, let t ∈ [a, b] and let m > N such

that kf

(t) − f (t)k

< ε/2. Next, it f ollows from the triangle inequality

that for all n > N ,

(t) −f(t)k

= kf

(t) −f

(t) + f

(t) −f(t)k

≤ kf

(t) −f

(t)k

+ kf

(t) −f(t)k

≤ |||f

− f

|||

∞,q

+ kf

(t) −f(t)k

< ε. (2.116)

Hence, since t ∈ [a, b] is arbitrary, it follows that {f

}

∞

n=0

converges to f

uniformly in t. Now, since f

(·) is continuous and convergence is uniform,

the limit function f(·) is also continuous.

NonlinearBook10pt November 20, 2007

68 CHAPTER 2

To see this, let t

∈ [a, b] be an arbitrary time in [a, b]. Since the

convergence of {f

}

∞

n=0

is uniform , given ε > 0, there exists suﬃ ciently

large n such that

(t) − f(t)k

< ε/3, t ∈ [a, b]. (2.117)

However, f

(t) is continuous at t

, and hence, there exists some δ > 0 such

that

(t) −f

< ε/3 (2.118)

whenever |t − t

| < δ. Thus, if |t − t

| < δ, it follows that

kf(t) −f (t

= kf(t) − f

(t) + f

(t) −f

) + f

) − f(t

≤ kf(t) − f

(t)k

+ kf

(t) −f

+ kf

) − f(t

< ε/3 + ε/3 + ε/3

= ε, (2.119)

which shows that f is continuous at t

. Now, since t

is an arbitrary point

in [a, b], it follows that f is continuous on [a, b]. Hence, since a sequence

of fu nctions {f

}

∞

n=0

in C[a, b] converges to a function f (·) ∈ C[a, b] if and

only if {f

(t)}

∞

n=0

converges to f(t) uniformly on [a, b], it follows that C[a, b]

endowed with the norm ||| ·|||

∞,q

is a Banach space. △

We close this section with a very important theorem from mathemat-

ical analysis needed to derive existence and uniqu en ess results for nonlinear

diﬀerential equations. T he theorem is known as the contraction mapping

theorem or the Banach ﬁxed point theorem. The following deﬁ nition is

needed for this r esult.

Deﬁnition 2.45. Let V be a linear vector space and let T : V → V.

The point x

∗

∈ V is a ﬁxed point of T (·) if T (x

∗

) = x

∗

Theorem 2.21 (Bana ch Fixed Point Theorem). Let X be a Banach

space with norm ||| · ||| : X → R and let T : X → X. Suppose there exists a

constant ρ ∈ [0, 1) s uch that

|||T (x) − T (y)||| ≤ ρ|||x − y|||, x, y ∈ X. (2.120)

Then there exists a unique x

∗

∈ X such that T (x

∗

) = x

∗

. Furthermore, for

each x

∈ X, the sequence {x

}

∞

n=0

⊂ X d eﬁ ned by

n+1

= T (x

) (2.121)

converges to x

∗

. Finally,

|||x

∗

− x

||| ≤

1 − ρ

|||T (x

) −x

|||, n ≥ 0. (2.122)

Proof. Let x

∈ X be arbitrary and deﬁne the sequence {x

}

∞

n=0

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 69

n+1

= T (x

). Now, for each n ≥ 0 it f ollows from (2.120) that

|||x

n+1

− x

||| = |||T (x

) − T (x

n−1

)|||

≤ ρ|||x

− x

n−1

|||

= ρ|||T (x

n−1

) − T (x

n−2

)|||

≤ ρ

|||x

n−1

− x

n−2

|||

≤ ρ

|||x

− x

|||

= ρ

|||T (x

) −x

|||. (2.123)

Next, let m = n + r, r ≥ 0, be given. Then (2.123) implies that

|||x

− x

||| = |||x

n+r

− x

|||

= |||x

n+r

− x

n+r−1

+ x

n+r−1

− x

n+r−2

+ ··· + x

n+1

− x

|||

≤ |||x

n+r

− x

n+r−1

||| + |||x

n+r−1

− x

n+r−2

||| + ··· + |||x

n+1

− x

|||

≤ (ρ

n+r−1

+ ρ

n+r−2

+ ··· + ρ

)|||x

− x

|||

(1 − ρ

)

1 −ρ

|||T (x

) − x

|||. (2.124)

Now, since ρ < 1, ρ

→ 0 as n → ∞. Hence, given ε > 0 and choosing a

large enough N, it follows th at |||x

− x

||| < ε for all m > n ≥ N. This

proves that the sequence {x

}

∞

n=0

is Cauchy. Furthermore, since X is a

Banach space, the sequence converges to an element x

∗

∈ X. Noting that

T (·) is a un iform ly continuous function, it follows that

T (x

∗

) = T ( lim

n→∞

) = lim

n→∞

T (x

) = lim

n→∞

n+1

= x

∗

, (2.125)

and h en ce, x

∗

is a ﬁxed point.

Next, suppose, ad absurdum, that x

∗

is not unique. That is, s uppose

there exists x ∈ X, x 6= x

∗

, s uch that T (x) = x. Then, it follows from

(2.120) that

|||x

∗

−x||| = |||T (x

∗

) −T (x)||| ≤ ρ|||x

∗

− x|||. (2.126)

Since ρ < 1, (2.126) holds only if |||x

∗

− x||| = 0, and hence, x

∗

= x leading

to a contradiction. Thus, x

∗

is a unique ﬁx ed point.

Finally, to show (2.122), let r → ∞ in (2.124) and recall that ||| · ||| :

X → R is continuous on X (see Problem 2.86) so that

|||x

∗

− x

||| = ||| lim

r→∞

n+r

− x

|||

= lim

r→∞

|||x

n+r

− x

|||

≤ lim

r→∞

(1 − ρ

)

1 −ρ

|||T (x

) − x

|||

NonlinearBook10pt November 20, 2007

70 CHAPTER 2

1 −ρ

|||T (x

) − x

|||, (2.127)

where the last inequality in (2.127) follows from the fact that ρ < 1.

It is important to note that it is not possible to replace (2.120) with

the weaker hypothesis

|||T (x) − T (y)||| < |||x −y|||, x, y ∈ X. (2.128)

See Problem 2.91. Finally, we give a slightly diﬀerent version of Theorem

2.21 for the case where T m ap s a closed subset S of X into itself. This

version of the theorem is useful in applications.

Theorem 2.22. Let X be a Banach space with norm ||| · ||| : X → R,

let S be a closed subset of X, and let T : S → S. Suppose there exists a

constant ρ ∈ [0, 1) s uch that

|||T (x) −T (y)||| ≤ ρ|||x − y|||, x, y ∈ S. (2.129)

Then there exists a un ique x

∗

∈ S such that T (x

∗

) = x

∗

. Furthermore, for

each x

∈ S, the sequence {x

}

∞

n=0

⊂ S deﬁned by x

n+1

= T (x

) converges

to x

∗

. Finally,

|||x

∗

− x

||| ≤

1 − ρ

|||T (x

) −x

|||, n ≥ 0. (2.130)

Proof. The fact that S is closed guarantees that x

∗

∈ S. Now, the

proof is identical to the proof of Theorem 2.21.

Finally, we present a key result connecting continuity and boun dedness

of a linear operator deﬁned on normed linear spaces. First, however, the

following deﬁnition is needed.

Deﬁnition 2.46. Let X and Y be normed linear spaces with norms

||| ·||| : X → R and |||· |||

′

: Y → R. A linear operator T : X → Y is bounded if

there exists α ≥ 0 such that |||T x|||

′

≤ α|||x||| for all x ∈ X.

Theorem 2.23. Let X and Y be normed linear spaces with norms

||| · ||| : X → R and ||| · |||

′

: Y → R, and let T : X → Y be a linear operator.

Then T is uniformly continuous on X if and only if T is bounded on X.

Proof. Assume T (·) is boun ded. Since T (·) is a linear operator, it

follows that

|||T (x) − T (y)|||

′

= |||T x − T y|||

′

= |||T (x − y)|||

′

≤ α|||x − y|||

for all x, y ∈ X and some α ≥ 0. Now, choosing δ = ε/α, it follows that

given ε > 0 there exists δ = δ(ε) such that |||T (x)−T (y)|||

′

< ε for all x, y ∈ X

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 71

satisfying |||x − y||| < δ. Hence, T (·) is uniformly continuous on X.

Conversely, assume T (·) is uniformly continuous on X. Then T (·) is

continuous at x = 0. Hence, given ε > 0 there exists δ = δ(ε) such that

|||x||| ≤ ε implies |||T (x)|||

′

= |||T x|||

′

≤ δ. Next, f or x ∈ X, x 6= 0, let y = βx,

where β = ε/|||x|||. Now, since |||y||| = |||βx||| = ε it follows that |||T y|||

′

≤ δ.

Hence,

|||T y|||

′

= |||T βx|||

′

= β|||T x|||

′

= ε

|||T x|||

′

|||x|||

≤ δ,

which implies that

|||T x|||

′

≤

|||x|||,

and h en ce, T (·) is bounded on X.

2.6 Dynamical Systems, Flows, and Vector Fields

As discussed in Chapter 1, a system is a combination of components or parts

which is perceived as a s ingle entity. T he parts making up the system are

typically clearly deﬁned with a particular set of variables, called the states

of the system, that completely determine the behavior of the system at a

given time. Hence, a dynamical system consists of a set of possible states in

a given space, together with a rule that determines the present state of the

system in terms of past states. Thus, a dynamical system on D ⊆ R

tells

us for a speciﬁc time t = t

and state x in the space D where the system

state x will be at time t ≥ t

. In this book, we view a dynamical system

as a precise mathematical object deﬁned on a time interval as a mapping

between vector spaces satisfying a set of axioms. For this deﬁ nition D is an

open s ubset of R

Deﬁnition 2.47. A dynamical system on D is the triple (D, R, s),

where s : R × D → D is such that the following axioms hold:

i) (Continuity): s(·, ·) is continuous on D×R and for every t ∈ R, s(·, x)

is continuously diﬀerentiable on D.

ii) (Con s istency): s(0, x

) = x

for all x

∈ D.

iii) (Group property): s(τ, s(t, x

)) = s(t + τ, x

) for all x

∈ D and

t, τ ∈ R.

Henceforth, we denote the dynamical system (D, R, s) by G and we

refer to the m ap s(·, ·) as the ﬂow or trajectory of G corresponding to x

∈ D,

and for a given s(t, x

), t ≥ 0, we refer to x

∈ D as an initial condition of G.

Given t ∈ R we denote the map s(t, ·) : D → D by s

) or s

. Hence, for

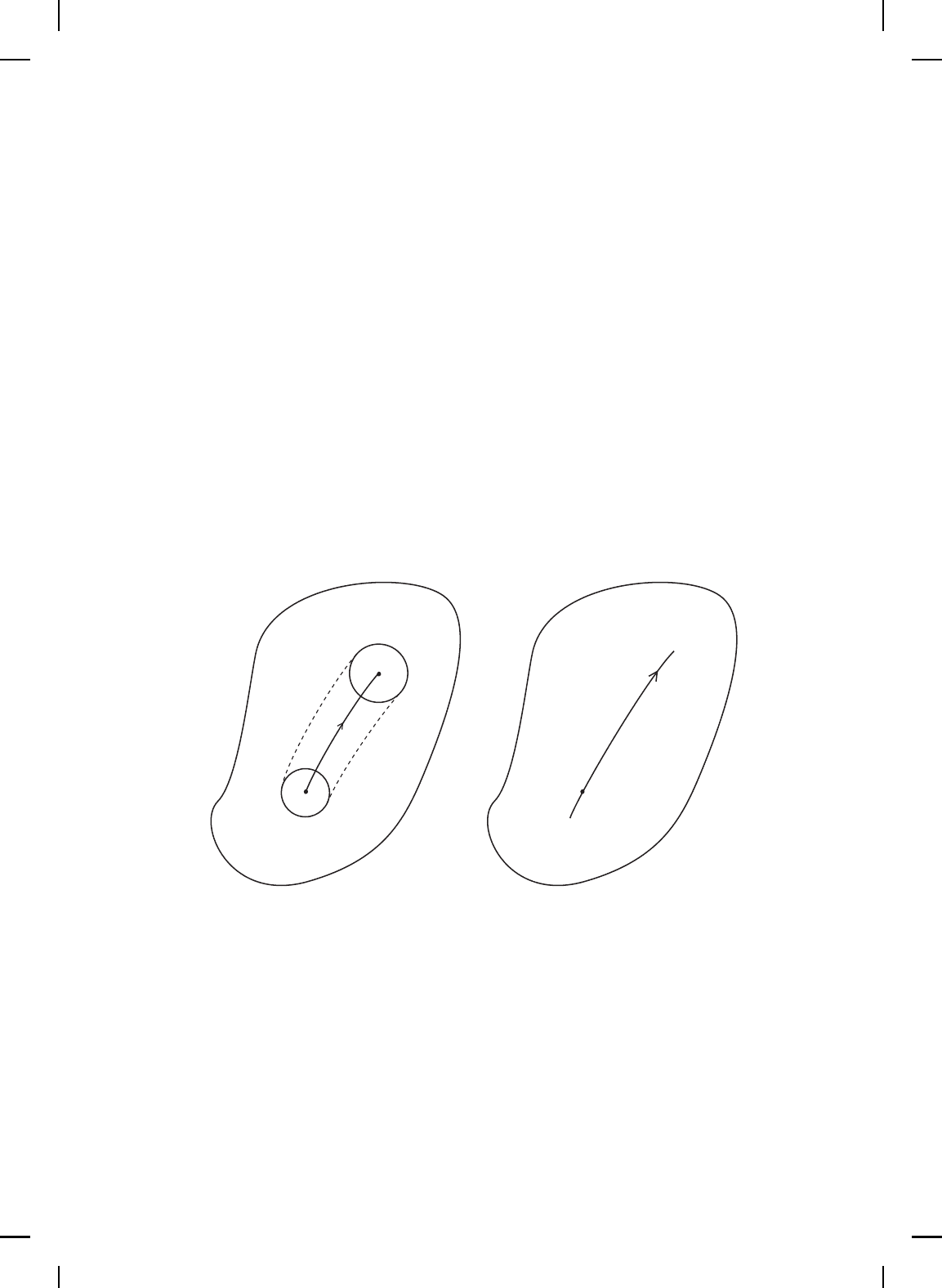
NonlinearBook10pt November 20, 2007

72 CHAPTER 2

t ∈ R the set of mappings deﬁned by s

) = s(t, x

) for every x

∈ D give

the ﬂow of G. In particular, if D

is a collection of initial conditions s uch

that D

⊂ D, th en the ﬂow s

: D

→ D is nothing more than the motion of

all points x

∈ D

or, equivalently, the image of D

⊂ D under the ﬂow s

that is, s

) ⊂ D (see Figure 2.3(a)). Alternatively, if the in itial condition

∈ D is ﬁxed and we let [α, β] ⊂ R, then the mapping s(·, x

) : [α, β] → D

deﬁnes the solution curve or trajectory of the dynamical system G. Hence,

the mapping s(·, x

) generates a graph in [α, β]×D identifying the trajectory

corresponding to motion along a curve C through the point x

in a subset

D of the state space (see Figure 2.3(b)). Given x ∈ D we denote the map

s(·, x) : R → D by s

(t) or s

If we think of a dynamical system G as describin g the motion of a ﬂuid,

then the ﬂow of G describes the motion of the entire ﬂuid and is consistent

with an Eulerian description of the dynamical system wherein the motion

is analyzed over a continuous medium (control volume). Alternatively, the

trajectory of G describes the motion of an individual particle in the ﬂu id

and is consistent with a Lagrangian formulation of the dynamical system

which describes the motion (position) of a particle as a function of time.



 



)

s(·, x

)

(a)

(b)

Figure 2.3 (a) Flow of a dynamical system. (b) Solution curve of a dynamical system.

In terms of the map s

: D → D Axioms ii) and iii) can be equivalently

written as ii)

′

) = x

and iii)

′

◦ s

)(x

) = s

)) = s

t+τ

Note that it follows from i) and iii) that the map s

: D → D is a continuous

function with a continuous inverse s

−t

. Thus, s

with t ∈ R generates a one-

parameter family of homeomorphisms on D forming a commutative group

under composition. To see that s

is one-to-one note that if s(t, y) = s(t, z),

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 73

then y = z follows from

y = s(0, y)

= s(−t + t, y)

= s(−t, s(t, y))

= s(−t, s(t, z))

= s(−t + t, z)

= s(0, z)

= z. (2.131)

Also note that if y ∈ D, then s

(x) = y for x = s(−t, y), and hence, s

onto. Finally, to see that s

has a continuous inverse we need only show that

−t

is the inverse of s

. To see this, note that for any two ﬂows s

and s

◦ s

= s

t+τ

since, for every x ∈ D,

◦ s

)(x) = s

(x)) = s

(s(τ, x)) = s(t + τ, x) = s

t+τ

(x). (2.132)

In addition, note that for every x ∈ D, s

(x) = s(0, x) = x is the identity

operator on D. Hence, s

−t

◦s

= s

t−t

= s

, which establishes that s

−t

is the

inverse of s

Since a dynamical system G involves the function s(·, ·) describing the

motion of x ∈ D for all t ∈ R, it generates a diﬀerential equation on D. In

particular, the function f : D → R

given by

f(x)

△

s(t, x)



t=0

(2.133)

deﬁnes a continuous vector ﬁeld on D. For x ∈ D, f(x) belongs to R

and

corresponds to the tangent vector to the curve s

(x) at t = 0. Hence, for

: D → D satisfying Axioms i)–iii) of Deﬁnition 2.47, letting x(t) = s(t, x

)

and d eﬁ ning f : D → R

as in (2.133) it follows that

˙x(t) = f(x(t)), x(0) = x

, t ∈ R. (2.134)

In this book, we use the notation s(t, x

), t ∈ R, and x(t), t ∈ R,

interchangeably to den ote the solution of the nonlinear dynamical system

(2.134) with initial condition x(0) = x

. Even though for physical dynamical

systems t ≥ 0, in this chapter we allow t ∈ R in order to d evelop general

analysis results for (2.134) possessing reversible ﬂows. In the later chapters

we consider dynamical systems on the semi-inﬁnite interval [0, ∞).

Example 2.30. In this examp le we analyze the solution curves and ﬂow

of a linear system. S peciﬁcally, deﬁne s : [0, ∞)×R

→ R

by s(t, x) = e

where A ∈ R

n×n

. Hence, s

: R

→ R

is represented by e

∈ R

n×n

so that

(x) = e

x. Note th at since e

n×n

= I

and e

A(t+τ)

= e

Aτ

it follows

that s

) = x

and (s

◦ s

)(x

) = s

)) = e

Aτ

, and h en ce,

NonlinearBook10pt November 20, 2007

74 CHAPTER 2

Axioms ii) and iii) of Deﬁnition 2.47 are satisﬁed. Axiom i) is trivially

satisﬁed. Now, for a given time t, if x ∈ R

the ﬂow s

(x) is the image

x of x and is given by e

x =

n=1

(i)

col

), where col

) denotes

the ith column of e

. Hence, the ﬂow is given by R(e

)

△

= {y ∈ R

y = e

x for some x ∈ R

} ⊆ R

for each ﬁxed time. Alternatively, given

∈ D, s

: [0, ∞ ) → R

deﬁnes the system trajectory. Hence, s

(·) is

represented by e

: [0, ∞) → R

so that s

= e

. Finally, to show

that s(t, x) = e

x generates a linear diﬀerential equation on R

note that

f(x) =

s(t, x)|

t=0

= Ax. Hence, with x(t) = s(t, x

) it

follows that

˙x(t) = Ax(t), x(0) = x

, t ≥ 0, (2.135)

which deﬁnes a linear, time-invariant dynamical system. △

2.7 Nonlinear Diﬀerential Equations

In Section 2.6 we saw that a nonlinear dynamical system G as deﬁned

by Deﬁnition 2.47 gives rise to a nonlinear diﬀerential equation. In this

section, we present several general r esults on nonlinear dynamical systems

characterized by d iﬀerential equations of the form

˙x(t) = f (x(t)), x(t

) = x

, t ∈ I

, (2.136)

where x(t) ∈ D, t ∈ I

, D is an open s ubset of R

with 0 ∈ D, f : D → R

continuous on D, and I

= (τ

min

, τ

max

) is the maximal interval of existence

for the solution x(·) of (2.136). A continuously diﬀerentiable function x :

→ D is said to be a solution to (2.136) on the interval I

⊆ R with

initial condition x(t

) = x

, if x(t) satisﬁes (2.136) for all t ∈ I

. Unlike

linear diﬀerential equations, the existence and uniqueness of solutions of

(2.136) are not guaranteed. In addition, a solution may only exist on some

proper subinterval (τ

min

, τ

max

) ⊂ R (maximal interval of existence). Note

that if x(·) is a solution to (2.136) and f : D → R

is continuous, then x(·)

satisﬁes the integral equation

x(t) = x

f(x(s))ds, t ∈ I

. (2.137)

Conversely, if x(·) is continuous on I

and s atisﬁes (2.137), then x(·) is

continuously diﬀerentiable on I

and satisﬁes (2.136). Hence, (2.136) and

(2.137) are equivalent in the sense that x(·) is a solution to (2.136) if and

only if x(·) is a solution to (2.137).

Since the existence and uniqueness of solutions for nonlinear diﬀeren-

tial equations are not always guaranteed, in this and the next section we

address the following questions: