Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 35

Note that in general the image of the intersection of two sets does not

necessarily equal the intersection of the images of the sets. However, this

statement is true if and only if f : X → Y is injective. (See P roblem 2.26.)

Theorem 2.8 also holds for unions and intersections of an arbitrary number

(inﬁnite or ﬁnite) of sets.

Theorem 2.9. Let X and Y be sets, let f : X → Y, let {A

: α ∈ I}

be an indexed family of sets in X, and let {B

: α ∈ J} be an indexed

family of sets in Y. Then the following statements hold:

i) f (

α∈I

) =

α∈I

f(A

ii) f

−1

(

α∈J

) =

α∈J

−1

iii) f

−1

(

α∈J

) =

α∈J

−1

Proof. The proof is similar to the proof of T heorem 2.8 and is left as

an exercise for the reader.

The next deﬁnition introduces the concept of convex functions deﬁned

on convex sets.

Deﬁnition 2. 20. Let C ⊆ R

be a convex set and let f : C → R. Then

f is convex if

f(µx

+ (1 − µ)x

) ≤ µf(x

) + (1 − µ)f(x

), (2.46)

for all x

, x

∈ C and µ ∈ [0, 1]. f is strictly convex if inequality (2.46) is

strict for all x

, x

∈ C such that x

6= x

and µ ∈ (0, 1).

Deﬁnition 2.21. Let D ⊆ R

and let f : D → R. For α ∈ R, the

set f

−1

(α)

△

= {x ∈ D : f (x) = α} is called the α-level set of f . T he set

−1

((−∞, α])

△

= {x ∈ D : f(x) ≤ α} is called the α-sub lev el set of f. For

β ∈ R, α ≤ β, the set f

−1

([α, β])

△

= {x ∈ D : α ≤ f(x) ≤ β} is called the

[α, β]- sublevel set of f .

Note that if f (x) = x

, then f

−1

(0) = {0}, and f

−1

(4) = {−2, 2},

whereas f

−1

((−∞, 4]) = [−2, 2]. The following proposition s tates that every

sublevel set of a convex f unction deﬁned on a convex set is convex.

Proposition 2.13. Let C ⊆ R

be convex and let f : C → R be convex.

Then f

−1

((−∞, α]), α ∈ R, is convex.

Proof. Let x

, x

∈ f

−1

((−∞, α]), α ∈ R, so that f(x

) ≤ α and

NonlinearBook10pt November 20, 2007

36 CHAPTER 2

f(x

) ≤ α. S ince f is convex in C, it follows that

f(µx

+ (1 − µ)x

) ≤ µf(x

) + (1 − µ)f(x

) ≤ α, (2.47)

for all x

, x

∈ f

−1

((−∞, α]), α ∈ R, and µ ∈ [0, 1]. Hence, µx

+(1−µ)x

∈

−1

((−∞, α]), α ∈ R, and hence, f

−1

((−∞, α]), α ∈ R, is convex.

Deﬁnition 2.22. Let D ⊆ R

and let f : D → R. The graph of f is

deﬁned by

△

= {(x, y) ∈ D × R : y = f(x)}.

The epigraph of f is deﬁned by

△

= {(x, y) ∈ D × R : y ≥ f(x)}.

Deﬁnition 2.23. L et D ⊂ R

. Then D is a hyperplane if there exists

µ ∈ R

, µ 6= 0, such that D = {x ∈ R

: µ

x = 0}.

The following two deﬁnitions introdu ce the notions of convergent

sequences of functions.

Deﬁnition 2.24. Let D ⊆ R

, f : D → R

, and f

: D → R

n = 1, . . .. A sequence of functions {f

}

∞

n=0

converges to f if, for every

x ∈ D, lim

n→∞

kf(x) − f

(x)k = 0 or, equivalently, for every ε > 0, there

exists N = N (ε, x) such that kf (x) − f

(x)k < ε for all n ≥ N.

Deﬁnition 2.25. Let D ⊆ R

, f : D → R

, and f

: D → R

n = 1, . . .. A sequ en ce of functions {f

}

∞

n=0

converges uniformly to f if, for

every ε > 0, there exists N = N (ε) such that kf(x) − f

(x)k < ε for all

x ∈ D and n ≥ N.

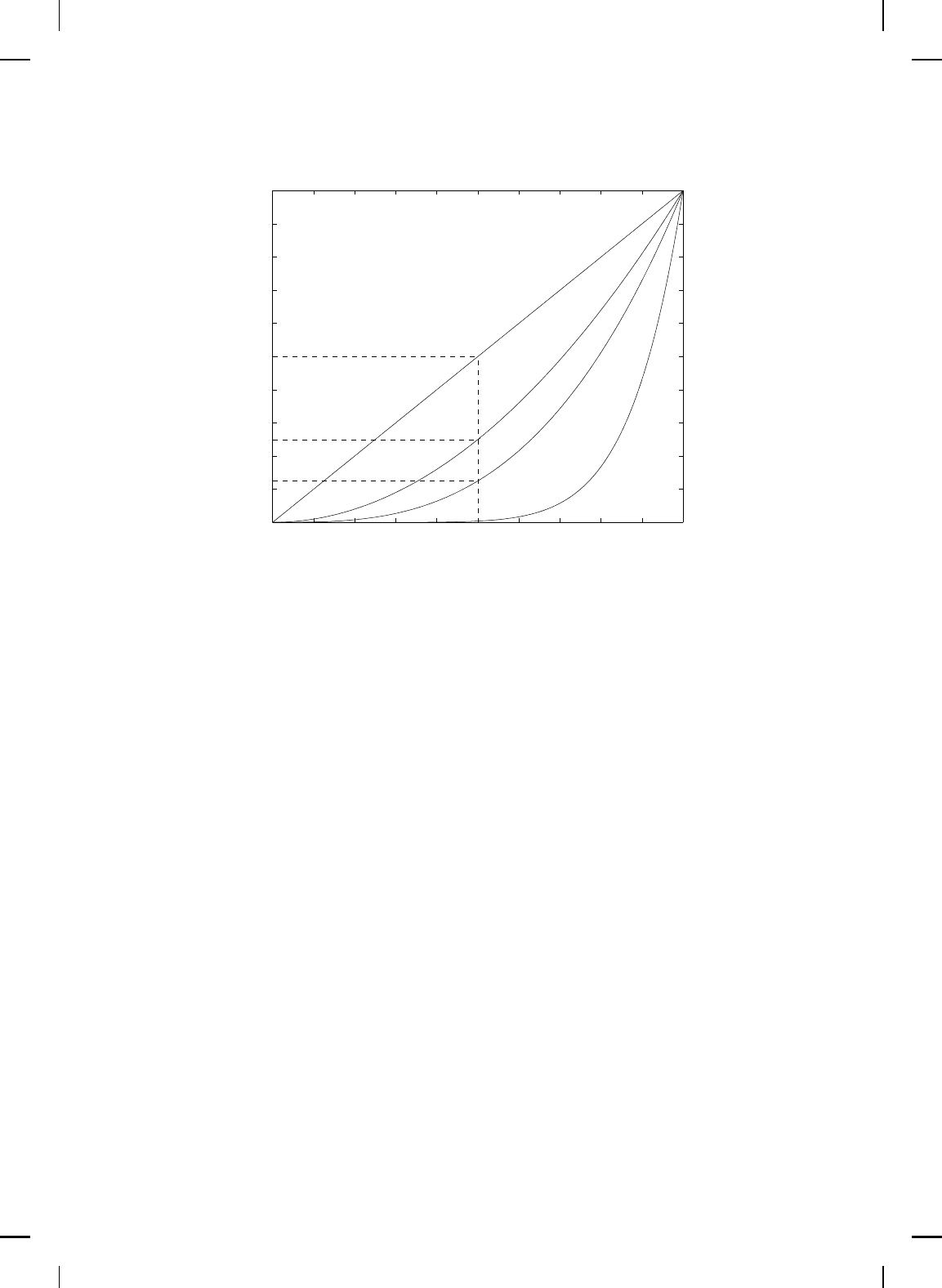
Example 2.13. Consider the inﬁnite sequence of functions {f

}

∞

n=1

where f

: [0, 1] → R is given by f

(x) = x

. This sequence has th e

form {x, x

, x

, . . .} and its limit depends on the value of x. In particular,

for 0 ≤ x < 1, the sequence converges to zero as n → ∞. For example, for

x = 1/2, {f

}

∞

n=1

= {

, . . . ,

, . . .}, which converges to zero as n → ∞.

For x = 1, however, {f

}

∞

n=1

= {1, 1, 1, . . .}, which converges to 1. Hence,

given ε > 0, there exists N = N(ε, x) such that |f(x)−x

| < ε for all n ≥ N

and 0 ≤ x ≤ 1, where f(x) = lim

n→∞

. Thus, the sequence converges

pointwise to f(x). However, the sequence does n ot converge uniformly to f .

To see th is, note that for every x ∈ [0, 1) we have |f(x)−x

| = |0−x

| = x

Choosing x ≈ 1, we can ens ure that x

> ε no matter how large N = N(ε) 6=

N(ε, x) is chosen. In particular, x

> ε implies that x >

√

ε, and hence,

any x ∈ (

√

ε, 1) will yield |f(x) − x

| > ε, n ≥ N , for N = N(ε). Hence,

the sequence of functions f

(x) do n ot converge uniformly to f. See Figure

2.1. △

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 37

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

1/2

1/8

1/4

Figure 2.1 Graphs for x

The next deﬁnition introduces the notion of monotonic functions

deﬁned on an interval I ⊆ R.

Deﬁnition 2. 26. Let I ⊆ R and let f : I → R. f is strictly increasing

on I if for every x, y ∈ I, x < y imp lies f(x) < f (y). f is increasing (or

nondecreasing) on I if for every x, y ∈ I, x < y implies f (x) ≤ f(y). f is

strictly decreasing on I if for every x, y ∈ I, x < y implies f(x) > f(y). f

is decreasing (or nonincreasing) on I if for every x, y ∈ I, x < y implies

f(x) ≥ f(y). f is monotonic on I if it is increasing on I or decreasing on I.

Note that if f is an increasing function, then −f is a decreasing

function. Hence, in many situations involving monotonic functions it suﬃ ces

to consider only the case of in creasing or decreasing functions.

Deﬁnition 2.27. Let D ⊆ R

and let f : D → R

. f is bounded on D

if there exists α > 0 such that kf(x)k ≤ α for all x ∈ D.

The next theorem shows that if a monotone function on R is bounded,

then its limit exists and is ﬁnite.

Theorem 2.10 (Monotone C onvergence Theorem). Let f : R → R

be decreasing (respectively, increasing) on R and assume that there exists

NonlinearBook10pt November 20, 2007

38 CHAPTER 2

γ ∈ R such that f (x) ≥ γ, x ∈ R (respectively, f(x) ≤ γ, x ∈ R). Then

lim

x→∞

f(x) exists.

Proof. Assume f is decreasing and bounded below, that is, there exists

γ ∈ R such that f(x) ≥ γ, x ∈ R. Let α = inf

x∈R

f(x) and note that α ≥ γ

since f(x) ≥ γ, x ∈ R. It follows from the deﬁnition of inﬁmum that for

every ε > 0 there exists x

∈ R such that α ≤ f (x

) < α + ε, which implies

that α ≤ f (x) < α + ε, x ≥ x

. Hence, for every ε > 0, there exists x

∈ R

such that 0 ≤ f(x) − α < ε, x ≥ x

, which implies that lim

x→∞

f(x) = α.

The proof f or the case where f is increasing and bounded above follows using

identical arguments and, hence, is omitted.

The next deﬁnition introdu ces the very important notion of continuity

of a function at a point. The n otion of continuity allows one to deduce the

behavior of a function in a neighborhood of a given point by using knowledge

of the value of the function at th at point.

Deﬁnition 2.28. Let D ⊆ R

, f : D → R

, and x ∈ D. Then f is

continuous at x ∈ D if, for every ε > 0, there exists δ = δ(ε, x) > 0 such that

kf(x) − f(y)k < ε for all y ∈ D satisfying kx − yk < δ. f is discontinuous

at x if f is not continuous at x.

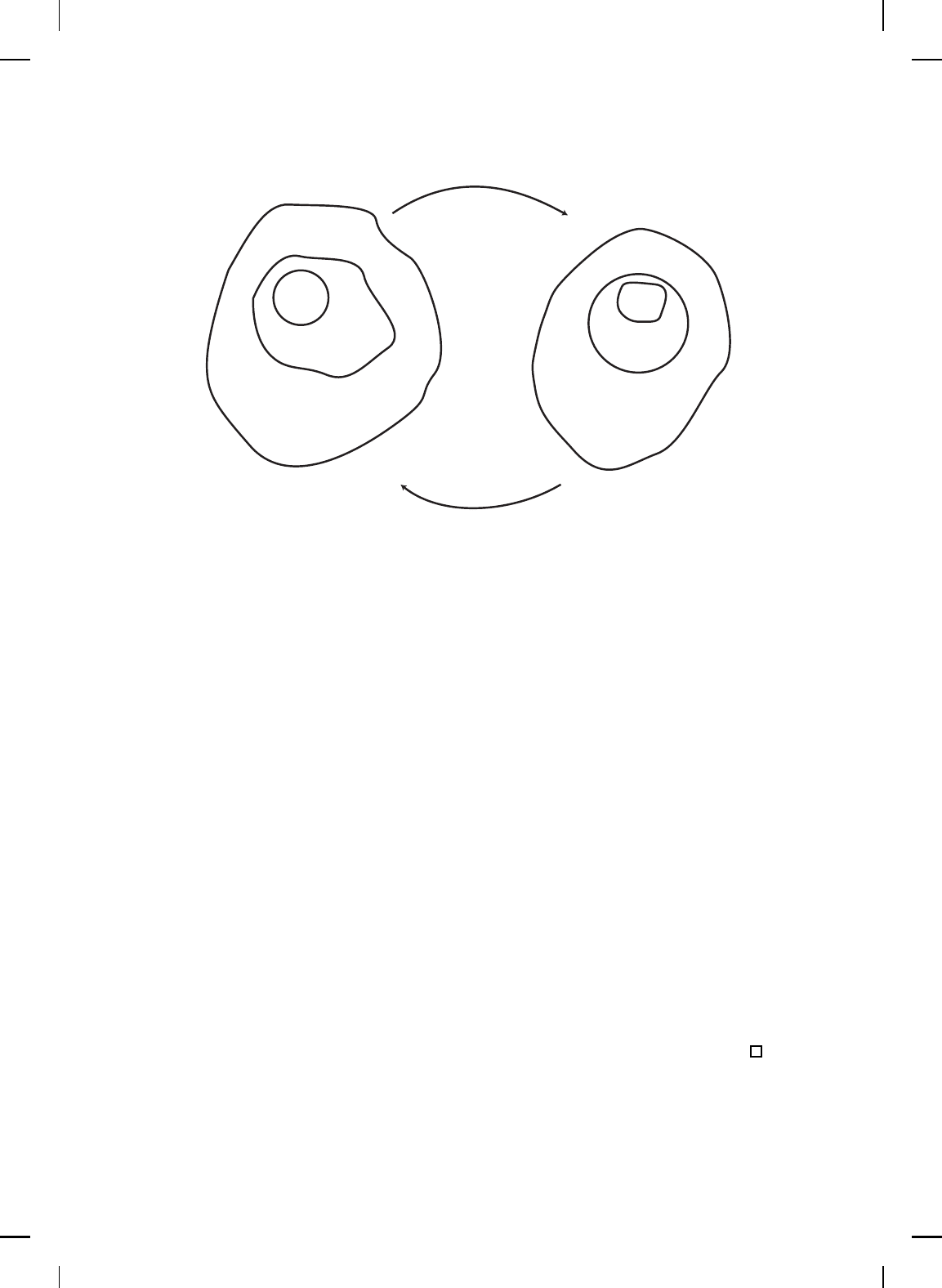
Deﬁnition 2.28 is equivalent to

f(B

(x)) ⊂ B

(f(x)). (2.48)

In particular, for every open ball B

(f(x)) there exists an open ball B

(x)

such that the points of B

(x) are mapped into B

(f(x)). It follows from

(2.48) that

(x) ⊂ f

−1

(f(x))), (2.49)

that is, the open ball B

(x) of rad ius δ > 0 and center x lies in the subset

−1

(f(x))) of D. (See Figure 2.2.)

An equivalent s tatement for continuity at a point can be given in terms

of convergent sequences. Speciﬁcally, f : D → R

is continuous at x if, for

every sequence {x

}

∞

n=1

⊂ D such that lim

n→∞

= x, lim

n→∞

f(x

) =

f(x) or, equivalently, lim

n→∞

f(x

) = f(lim

n→∞

). To see the equivalence

between this deﬁnition and Deﬁnition 2.28, assume f is continuous at x

that for every ε > 0 there exists δ > 0 such that kx − x

k < δ imp lies

kf(x) − f(x

)k < ε, x ∈ D . Now, take any sequence {x

}

∞

n=1

⊂ D wh ich

converges to x

∈ D. Hence, for the given δ > 0, th ere exists an integer

N such that n > N implies kx

− x

k < δ. Sin ce kf(x) − f(x

)k < ε

whenever x ∈ D and kx − x

k < δ, it follows that kf(x

) − f(x

)k < ε for

n > N , and hence, {f(x

)}

∞

n=1

converges to f (x

). This shows suﬃciency.

To show necessity, assume for every sequence {x

}

∞

n=1

⊂ D such that x

→

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 39

(x)

−1

(f(x)))

(f(x))

f(x)

−1

Figure 2.2 Continuity of f : X → Y at x.

, f(x

) → f (x

) as n → ∞. Now, suppose, ad absurdum, for some

ε > 0 and every δ > 0 there exists x ∈ D such that kx − x

k < δ and

kf(x) − f (x

)k ≥ ε. Choose δ = 1/n, n = 1, 2, . . .. This implies there exists

a corresponding sequence of points {x

}

∞

n=1

⊂ D such that kx

−x

k < 1/n

and kf (x

) − f(x

)k ≥ ε. Clearly, the sequence {x

}

∞

n=1

converges to x

;

however, the sequence {f (x

)}

∞

n=1

does n ot converge to f(x

), leading to a

contradiction. This proves necessity.

The function f is said to be continuous on D if f is continuous at every

point x ∈ D. The next proposition establishes the fact that the continuous

image of a compact set is compact.

Proposition 2.14. Let D

⊂ R

be a compact set and let f : D

→ R

be continuous on D

. Then the image of D

under f is compact.

Proof. Let {y

}

∞

n=1

be a sequence in the range of f. In this case, there

exists a corresponding sequence {x

}

∞

n=1

⊂ D

such that y

= f (x

). Since

is compact, it follows f rom Theorem 2.4 that there exists a subsequence

}

∞

k=1

⊆ {x

}

∞

n=1

such that lim

k→∞

= x ∈ D

. Now, since f is

continuous it follows that lim

k→∞

f(x

) = f(lim

k→∞

) = f(x) ∈ f (D

Hence, {y

}

∞

n=1

has a convergent subsequence in f (D

), and hence, by

Theorem 2.4, f (D

) is compact.

It is important to note that th e existence of δ in Deﬁnition 2.28 is in

NonlinearBook10pt November 20, 2007

40 CHAPTER 2

general dependent on both ε and x. In the case where δ is not a function of

the point x we have the stronger notion of uniform continuity over the set

Deﬁnition 2.29. Let D ⊆ R

and f : D → R

. Then f is uniformly

continuous on D if, for every ε > 0, there exists δ = δ(ε) > 0 such that

kf(x) − f(y)k < ε for all x, y ∈ D satisfying kx − yk < δ.

Note that if f : D → R

is un iformly continuous on D, then f is

continuous at every x ∈ D. The converse of this statement, however, is not

true.

Example 2.14. The function f : (0, ∞) → R deﬁned by f(x) = 1/x

is continuous at every point in (0, ∞) but is not uniformly continuous on

(0, ∞). For example, let D = (0, 1). Clearly, f is continuous on D but not

uniformly continuous on D. To see this, let ε > 1 be such that 1/ε < δ, and

let x = 1/ε and y = 1/(ε + 1). Note that x, y ∈ D. In this case,

|x −y| =



−

ε + 1



ε(ε + 1)

< δ.

However,

|f(x) −f (y)| = |ε −(ε + 1)| = 1 > ε.

Hence, for these two points we have |f (x) −f(y)| > ε whenever |x −y| < δ,

contradicting the deﬁnition of uniform continuity. △

Example 2. 15. The function f : D → R deﬁned by f (x) = x

uniformly continuous on D = (0, 1]. To see this, note that for all x, y ∈ D,

|f(x) − f(y)| = |x

− y

| = |(x − y)(x + y)| ≤ 2|x − y|.

If |x − y| < δ, then |f(x) − f (y)| < 2δ. Hence, given ε > 0, we need only

take δ = ε/2 to guarantee that |f (x) − f (y)| < ε for every x, y ∈ D such

that |x − y| < δ. Since δ is independent of x, this shows uniform continuity

on D. △

Example 2.16. The function f : D → R deﬁned by f(x) = 1/(x

+1) is

uniformly continuous on D = [−1, 1]. To see this, note that for all x, y ∈ D,

|f(x) −f(y)| =



+ 1

−

+ 1



(y − x)(y + x)

+ 1)(y

+ 1)



|y −x||y + x|

+ 1||y

+ 1|

≤ |y − x||y + x|

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 41

≤ (|y| + |x|)|y − x|

≤ 2|y − x|.

Hence, given ε > 0 we need only take δ = ε/2 to guarantee that |f(x) −

f(y)| < ε for every x, y ∈ D whenever |x − y| < δ. In particular, |f (x) −

f(y)| ≤ 2|x − y| < 2δ = ε. Since δ is independent of x, this shows uniform

continuity on D. △

Example 2.17. The signum function sgn : R → {−1, 0, 1} is deﬁned as

sgn x

△

= x/|x|, x 6= 0, and sgn(0)

△

= 0. Since lim

x→0

sgn(x) = 1 6= sgn(0),

the signum function is discontinuous at x = 0. △

Example 2.16 shows that if a continuous fu nction is deﬁned on a

compact set, then the function is uniformly continuous. In other words, for

compact sets, continuity implies uniform continuity. This fact is established

in the following proposition.

Proposition 2.15. Let D

⊂ R

be a compact set and let f : D

→ R

be continuous on D

. Then f is uniformly continuous on D

Proof. Suppose, ad absurdum, that f is not uniformly continuous

on D

. In this case, there exists ε > 0 for w hich no δ = δ(ε) > 0 exists

such that kf (x) − f(y)k < ε for all x, y ∈ D

satisfying kx − yk < δ. In

particular, none of the δ’s given by δ = 1/2, 1/3, . . . , 1/n, . . . can be used.

Hence, for each n ∈ Z

, there exist x

, y

∈ D

such that kx

− y

k < 1/n

and kf (x

) −f (y

)k ≥ ε. Since D

is compact, it follows from Theorem 2.4

that there exists a convergent subsequence {x

}

∞

k=1

⊆ {x

}

∞

n=1

⊆ D

such

that

lim

k→∞

= x, x ∈ D

. (2.50)

Now, using the fact that kx

−y

k < 1/n and kf(x

)−f (y

)k ≥ ε, it follows

that

lim

k→∞

−y

) = 0. (2.51)

Next, subtracting (2.51) from (2.50) yields lim

k→∞

= x. Since f is

continuous it follows that

lim

k→∞

[f(x

) − f(y

)] = f(x) −f (x) = 0,

which implies that, for large en ough k ∈ Z

, kf(x

) − f(y

)k < ε. This

leads to a contradiction.

Continuity can alternatively be characterized by the following propo-

sition.

Proposition 2.16. Let D ⊆ R

and let f : D → R

. Then f is

NonlinearBook10pt November 20, 2007

42 CHAPTER 2

continuous on D if and only if, for every open (respectively, closed) set

Q ⊆ R

, the inverse image f

−1

(Q) ⊆ D of Q is open (respectively, closed)

relative to D.

Proof. Let f be continuous on D, let Q ⊆ R

be open, and let x ∈

−1

(Q), that is, y

△

= f (x) ∈ Q. Since Q is open it follows that there exists

ε > 0 such that B

(y) ⊆ Q, and since f is continuous at x it follows that

there exists δ > 0 such th at f(ˆx) ∈ B

(y) for all ˆx ∈ B

(x) or, equivalently,

f(B

(x)) ⊆ B

(y). Hence,

(x) ⊆ f

−1

(f(B

(x))) ⊆ f

−1

(y)) ⊆ f

−1

(Q),

which shows that f

−1

(Q) is open relative to D.

Conversely, assume that f

−1

(Q) is open relative to D for every open

Q ⊆ R

. Let x ∈ D and let y = f (x). Since for every ε > 0, B

(y) is

open in R

it follows that f

−1

(y)) is open relative to D. Now, since

x ∈ f

−1

(y)), there exists δ > 0 such that B

(x) ⊆ f

−1

(y)), which

proves that f is continuous at x.

Finally, the p roof of the statement f is continuous on D if and only if,

for every closed set Q ⊆ R

, the inverse image f

−1

(Q) ⊆ D of Q is closed

relative to D is analogous to the proof given above and, hence, is omitted.

It follows from Proposition 2.16 that every level set and every sublevel

set of a continuous scalar-valued function is closed relative to the domain of

the fun ction.

It is important to note that bou ndedness is not preserved by a

continuous mapping. For example, consider the continuous function f (x) =

1/x and consider the bounded set Q

△

= (0, 1). Then f(Q) = (1, ∞) is

not bounded. However, as shown in the next proposition, boundedness is

preserved under a uniformly continuous mapping.

Proposition 2. 17. Let D ⊆ R

, let Q ⊆ D be bounded, and let f :

D → R

be uniform ly continuous on Q. Then f(Q) is bounded.

Proof. Let ε > 0 be given. Since f is u niformly continuous on Q, there

exists δ > 0 such that kf(x)−f (y)k < ε for all x, y ∈ Q such that kx−yk < δ.

Now, since Q is bounded, there exists a ﬁnite s ubset

Q = {x

, . . . , x

}

of Q such that, for each x ∈ Q, there exists k ∈ {1, 2, . . . , q} such that

kx − x

k < δ. Next, deﬁne

△

= max

1≤i,j≤q

kf(x

) −f (x

)k.

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 43

Now, let x, y ∈ Q and x

, x

∈

Q be such that kx−x

k < δ and ky −x

k < δ.

Then,

kf(x) −f(y)k ≤ kf(x) − f(x

)k + kf(x

) − f(x

)k + kf(x

) −f(y)k

≤ 2ε + β.

Hence, f (Q) is bounded.

Even though the image of a bounded set under a continuous map ping

is not necessarily bounded, the image of a compact set under a continuous

function is compact. An identical statement is true f or connected sets. For

details see Problem 2.54.

Example 2.18. Let D ⊂ R and let f : D → R be given by f (x) = 1/x.

For D = (1, 2), f is bounded on D since inf{1/x : 1 < x < 2} = 1/2 and

sup{1/x : 1 < x < 2} = 1. For D = [2, ∞), f is also bounded on D since

inf{1/x : x ≥ 2} = 0 and sup{1/x : x ≥ 2} = 1/2. In this case, however,

the inﬁmum of zero is not attained since the set {1/x : x ≥ 2} does not

contain zero. Finally, note that for D = (0, 1), f is not bounded on D since

sup{1/x : 0 < x < 1} = ∞. △

The next deﬁnition introduces the notion of lower semicontinuous and

upper semicontinuous functions at x ∈ D.

Deﬁnition 2.30. Let D ⊆ R

, f : D → R, and x ∈ D. f is lower

semicontinuous at x ∈ D if for every sequ en ce {x

}

∞

n=0

⊂ D such that

lim

n→∞

= x, f(x) ≤ lim inf

n→∞

f(x

Note that a function f : D → R is lower semicontinuous at x ∈ D if

and only if for each α ∈ R the set {x ∈ D : f (x) > α} is open. Alternatively,

a bounded function f : D → R is lower semicontinuous at x ∈ D if and only

if for each ε > 0 there exists δ > 0 such that kx − yk < δ, y ∈ D, imp lies

f(x) −f(y) ≤ ε.

Deﬁnition 2.31. Let D ⊆ R

, f : D → R, and x ∈ D. f is upper

semicontinuous at x ∈ D if for every sequ en ce {x

}

∞

n=0

⊂ D such that

lim

n→∞

= x, f(x) ≥ lim sup

n→∞

f(x

), or, equivalently, for each α ∈ R

the set {x ∈ D : f (x) < α} is open.

As in the case of continuous functions, a function f is said to be lower

(respectively, upper) semicontinuous on D if f is lower (respectively, upper)

semicontinuous at every point x ∈ D. Clearly, if f is both lower and upper

semicontinuous, then f is continuous. The function f(x) = −1 for x < 0

and f (x) = 1 for x ≥ 0 is upper semicontinuous at x = 0, but not lower

semicontinuous at x = 0. The ﬂoor function f (x) = ⌊x⌋, which returns the

NonlinearBook10pt November 20, 2007

44 CHAPTER 2

greatest integer less than or equal to a given x, is upper semicontinuous on

R. Similarly, the ceiling function f(x) = ⌈x⌉, which return s the smallest

integer greater than or equal to a given x, is lower semicontinuous on R.

Next, we present three key theorems due to Weierstrass involving

the existence of global minimizers and maximizers of lower and upper

semicontinuous functions on compact sets.

Theorem 2.11 (Weierstrass T heorem). Let D

⊂ R

be compact and

let f : D

→ R be lower semicontinuous on D

. Then there exists x

∗

∈ D

such that f (x

∗

) ≤ f(x), x ∈ D

Proof. Let {x

}

∞

n=0

⊂ D

be a sequence such that lim

n→∞

f(x

) =

inf

x∈D

f(x). Since D

is bounded, it follows from the Bolzano-Weierstrass

theorem (Theorem 2.3) that every sequence in D

has at least one

accumulation point x

∗

. Now, since D

is closed, x

∗

∈ D

, and since f (·)

is lower semicontinuous on D

, it follows that f (x

∗

) ≤ lim

n→∞

f(x

) =

inf

x∈D

f(x). Hence, f (x

∗

) = inf

x∈D

f(x).

Theorem 2.12. Let D

⊂ R

be compact and let f : D

→ R be upper

semicontinuous on D

. Then there exists x

∗

∈ D

such th at f (x

∗

) ≥ f (x),

x ∈ D

Proof. The proof is identical to the proof of Theorem 2.11.

The following theorem combines Theorems 2.11 and 2.12 to s how that

continuous functions on compact sets attain a minimum and maximum.

Theorem 2.13. Let D

⊂ R

be compact and let f : D

→ R be

continuous on D

. Then there exist x

min

∈ D

and x

max

∈ D

such that

f(x

min

) ≤ f(x), x ∈ D

, and f(x

max

) ≥ f(x), x ∈ D

Proof. Since f is continuous on D

if and only if f is both lower and

upper semicontinuous on D

, the result is a direct consequence of Theorems

2.11 and 2.12.

A s lightly weaker notion of a continuous fu nction on an interval I ⊂ R

is a piecewise continuous function on I, wherein the function is continuous

everywhere on an interval except possibly at a ﬁnite number of points in

every ﬁnite interval. For the next deﬁnition, recall that an interval is a

connected subset of R and for an interval I ⊆ R, the endpoints of I are the

boundary points of I that belong to I.

Deﬁnition 2.32. L et I ⊆ R and let f : I → R

. Then f is piecewise

continuous on I if for every bou nded su binterval I

⊂ I, f is continuous