Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 15

Now, letting q = p/(p − 1) and ap plying H¨older’s inequality (2.18) to each

of the summations on the right-hand side of (2.15) yields

i=1

(i)

+ y

(i)

≤

i=1

(i)

+ y

(i)

(p−1)q

1/q





i=1

(i)

1/p

i=1

(i)

1/p





i=1

(i)

+ y

(i)

1/q





i=1

(i)

1/p

i=1

(i)

1/p





. (2.16)

Next, dividing both sides of (2.16) by



i=1

(i)

+ y

(i)



1/q

and using the

fact that 1 −1/q = 1/p we obtain

i=1

(i)

+ y

(i)

1/p

≤

i=1

(i)

1/p

i=1

(i)

1/p

, (2.17)

which proves the result.

The notation k ·k

does n ot explicitly refer to the dimension of R

which it is applied. We assume this is implied by context. I n the case where

p = 1,

kxk

i=1

(i)

is called the absolute sum norm; the case p = 2,

kxk

i=1

(i)

1/2

= (x

1/2

is called the Euclidean norm; and th e case p = ∞,

kxk

∞

= max

i=1,...,n

(i)

is called the inﬁnity n orm.

The next result is kn own as H¨older’s inequality. For this result (and

henceforth) we interpret 1/∞ = 0.

Proposition 2.3. Let x, y ∈ R

, and let 1 ≤ p ≤ ∞ and 1 ≤ q ≤ ∞

satisfy 1/p + 1/q = 1. Then

y| ≤ kxk

kyk

. (2.18)

Proof. The cases p = 1, ∞ and q = ∞, 1 are straightforward and are

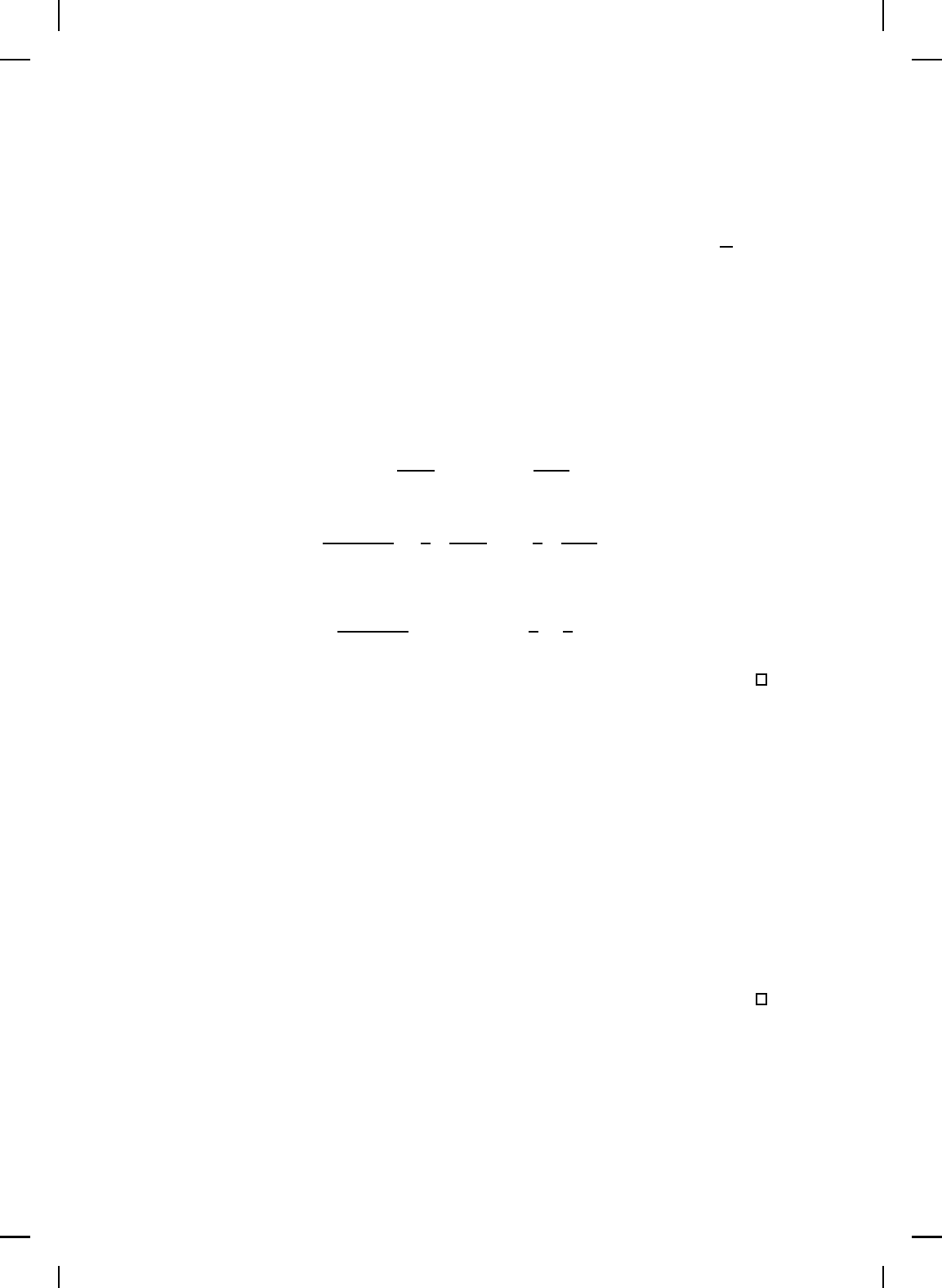
NonlinearBook10pt November 20, 2007

16 CHAPTER 2

left as an exercise for the reader. Assume 1 < p < ∞ so that 1 < q < ∞.

For u ≥ 0, v ≥ 0, and α ∈ (0, 1) note that

(1−α)

≤ αu + (1 − α)v, (2.19)

with equality holding in (2.19) if and only if u = v. To see this, let f : R

→

R be deﬁned by f (z)

△

= z

−αz + α −1 and note that f

′

(z) = α(z

(α−1)

−1).

Since α ∈ (0, 1) it follows that f

′

(z) > 0 for all z ∈ (0, 1) and f

′

(z) < 0 for

all z > 1. Now, it follows that for z ≥ 0, f (z) ≤ f (1) = 0 w ith equality

holding for z = 1. Hence, z

≤ αz + 1 − α with equality holding for z = 1.

Taking z = u/v, v 6= 0, yields (2.19), while for v = 0 (2.19) is trivially

satisﬁed.

Now, for each i ∈ {1, . . . , n}, α = 1/p, and 1 − α = 1/q, on setting

u =



(i)

kxk



, v =



(i)

kyk



, (2.20)

(2.19) yields

(i)

kxk

kyk

≤



(i)

kxk





(i)

kyk



. (2.21)

Summing over [1, n] yields

kxk

kyk

i=1

(i)

| ≤

= 1, (2.22)

which proves (2.18).

The case p = q = 2 is known as the Cauchy-Schwarz inequality. Since

this result is important, we state it as a corollary.

Corollary 2.1. Let x, y ∈ R

. Then

y| ≤ kxk

kyk

. (2.23)

Proof. Note th at for x = 0 or y = 0 the inequality is immediate. Next,

note that for λ ∈ R,

(x − λy)

(x − λy) = x

x − 2λx

y + λ

= kxk

− 2λx

y + λ

kyk

≥ 0, x, y ∈ R

. (2.24)

Now, taking λ = x

y/kyk

yields the result.

Two norms k · k and k · k

′

on R

are equivalent if there exist positive

constants α, β such that

αkxk ≤ kxk

′

≤ βkxk, (2.25)

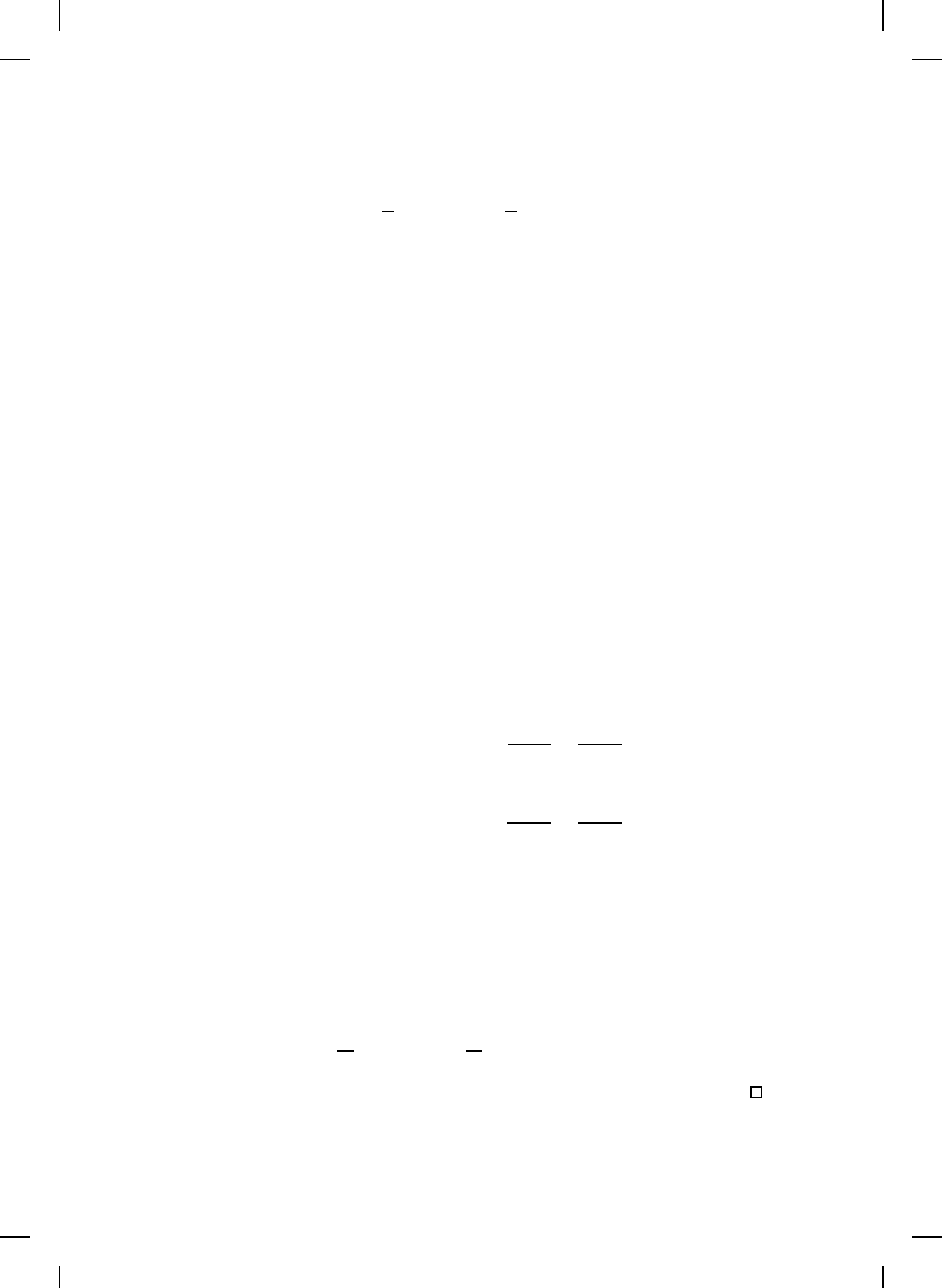
NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 17

for all x ∈ R

. Note that (2.25) can be written as

kxk

′

≤ kxk ≤

kxk

′

Hence, the word “equivalent” is justiﬁed. The next result shows that all

norms are equivalent in ﬁnite-dimensional spaces.

Theorem 2.1. If k·k and k·k

′

are vector norms on R

, then k·k and

k ·k

′

are equivalent.

Proof. Let x, y ∈ R

and note that

kx −yk =



i=1

− y



≤

i=1

− y

|ke

≤ Ckx − yk

∞

where C

△

= max

i=1,...,n

k. Similarly, it can be shown th at kx − yk

′

≤

′

kx − yk

∞

, where C

′

△

= max

i=1,...,n

′

. Hence, it follows that k · k and

k ·k

′

are continuous on R

with respect to k · k

∞

Next, since {x ∈ R

: kxk

∞

= 1} is a compact set (see Deﬁnition 2.14)

it follows from Weierstrass’ theorem (Theorem 2.13) that there exists α, β >

0 such that α = m in

{x∈R

:kxk

∞

=1}

kxk and β = max

{x∈R

:kxk

∞

=1}

kxk. Now

it follows that

α = min

{x∈R

:kxk

∞

=1}

kxk = min

{x∈R

:kxk

∞

6=0}

kxk

∞

≤

kxk

∞

, x 6= 0, (2.26)

and

β = max

{x∈R

:kxk

∞

=1}

kxk = max

{x∈R

:kxk

∞

6=0}

kxk

∞

≥

kxk

∞

, x 6= 0, (2.27)

which implies that

αkxk

∞

≤ kxk ≤ βkxk

∞

, x ∈ R

. (2.28)

Similarly, it can be s hown that

′

kxk

∞

≤ kxk

′

≤ β

′

kxk

∞

, x ∈ R

, (2.29)

where α

′

= min

{x∈R

:kxk

∞

=1}

kxk

′

and β

′

= max

{x∈R

:kxk

∞

=1}

kxk

′

. Now it

follows from (2.28) and (2.29) that

′

kxk

′

≤ kxk ≤

′

kxk

′

, x ∈ R

, (2.30)

which proves the equivalence of k ·k and k · k

′

NonlinearBook10pt November 20, 2007

18 CHAPTER 2

The notion of vector norms allows us to deﬁne a matrix norm by

viewing a matrix A ∈ R

n×m

as a vector in R

, for example, as vec A,

where vec(·) den otes the column s tacking operator.

Deﬁnition 2.7. A matrix norm k · k on R

n×m

is a function k · k :

n×m

→ R that satisﬁes the following axioms:

i) kAk ≥ 0, A ∈ R

n×m

ii) kAk = 0 if and only if A = 0.

iii) kαAk = |α|kAk, α ∈ R.

iv) kA + Bk ≤ kAk+ kBk, A, B ∈ R

n×m

If k·k is a vector norm on R

, then k·k

′

deﬁned by kAk

′

= kvec Ak

is a matrix norm on R

n×m

. For example, the p-norms can be extended to

matrices in this way. Hence, for A ∈ R

n×m

deﬁne

kAk

△





i=1

j=1

(i,j)





1/p

, 1 ≤ p < ∞,

kAk

∞

△

= max

i=1,...,n,j=1,...,m

(i,j)

Note that we use the same symbol k · k

to denote the p-norm for both

vectors and matrices. This notation is consistent since if A ∈ R

n×1

, then

kAk

coincides with the vector p-norm. Furthermore, if A ∈ R

n×m

, then

kAk

= kvec Ak

. (2.31)

The matrix p-norms in the cases p = 1, 2, ∞ are the most commonly

used. In particular, when p = 2 we write kAk

△

= kAk

, where k·k

is called

the Frobenius norm. Since kAk

= kvec Ak

, we have

kAk

= kAk

= kvec Ak

. (2.32)

It is easy to see that kAk

= (tr AA

)

1/2

for all A ∈ R

n×m

Let k · k, k · k

′

, and k · k

′′

denote matrix norms on R

n×l

, R

n×m

, and

m×l

, respectively. We say (k ·k, k ·k

′

, k ·k

′′

) is a submultiplicative triple of

matrix norms with constant δ > 0 if

kABk ≤ δkAk

′

kBk

′′

, (2.33)

for all A ∈ R

n×m

and B ∈ R

m×l

. If δ = 1, then we may omit the phrase

“with constant 1.” If k · k is a norm on R

n×n

and

kABk ≤ kAkkBk, (2.34)

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 19

for all A, B ∈ R

n×n

, then we say that k · k is submultiplicative. That is,

a matrix norm k · k on R

n×n

is submultiplicative if (k · k, k · k, k · k) is a

submultiplicative tr iple of matrix norms with constant 1. We see in (2.34)

with n = 2, for example, that k · k

, 1 ≤ p ≤ 2, is submultiplicative. If a

submultiplicative matrix norm k · k on R

n×n

satisﬁes kI

k = 1, then we say

k ·k is normalized.

A special case of sub multiplicative triples is the case in which B is a

vector, that is, l = 1. Hence, for A ∈ R

n×m

and x ∈ R

consider (setting

δ = 1)

kAxk ≤ kAk

′

kxk

′′

, (2.35)

where k · k, k · k

′

, and k · k

′′

are norms on R

, R

n×m

, and R

, respectively.

If n = m and k · k = k ·k

′′

, that is,

kAxk ≤ kAk

′

kxk,

then we say that k ·k and k · k

′

are compatible.

We now consider a very special class of matrix norms, namely, the

induced matrix norms w herein (2.35) holds as an equality.

Deﬁnition 2.8. Let k · k and k · k

′

be vector norms on R

and R

respectively. Then the function k ·k

′′

: R

n×m

→ R deﬁned by

kAk

′′

= m ax

{x∈R

: x6=0}

kAxk

′

kxk

(2.36)

is called an induced matrix norm.

It can be shown that (2.36) is equivalent to each of the expressions

kAk

′′

= max

{x∈R

: kxk≤1}

kAxk

′

, (2.37)

kAk

′′

= max

{x∈R

: kxk=1}

kAxk

′

. (2.38)

In this case, we say k·k

′′

is induced by k·k and k·k

′

. If m = n and k·k = k·k

′

then we say that k · k

′′

is induced by k · k and we call k · k

′′

an equi-induced

norm. It remains to be shown , however, that k · k

′′

deﬁned by (2.36) is

indeed a matrix norm.

Theorem 2.2. Every induced matrix norm is a m atrix norm.

Proof. Let k·k and k·k

′

be vector norms on R

and R

, respectively,

and let k · k

′′

: R

n×m

→ R be deﬁned as in (2.36) or, equivalently, (2.38).

Clearly, k·k

′′

satisﬁes Axioms i)–iii) of Deﬁnition 2.7. To show that Axiom

NonlinearBook10pt November 20, 2007

20 CHAPTER 2

iv) holds, let A, B ∈ R

n×m

and n ote that

kA + Bk

′′

= max

{x∈R

: kxk=1}

k(A + B)xk

′

= max

{x∈R

: kxk=1}

kAx + Bxk

′

≤ max

{x∈R

: kxk=1}

(kAxk

′

+ kBxk

′

)

≤ max

{x∈R

: kxk=1}

kAxk

′

+ max

{x∈R

: kxk=1}

kBxk

′

= kAk

′′

+ kBk

′′

Hence, k ·k

′′

: R

n×m

→ R is a matrix norm on R

n×m

In the notation of (2.36),

kAk

′′

= max

{x∈R

: x6=0}

kAxk

′

kxk

≥

kAxk

′

kxk

, x 6= 0.

Hence,

kAxk

′

≤ kAk

′′

kxk.

In this case, (k · k

′

, k · k

′′

, k · k) is a submultiplicative triple. If m = n and

k·k = k·k

′

, then the induced norm k·k

′′

is compatible with k·k. The next

result shows that submultiplicative trip les of matrix norms can be obtained

from induced matrix norms.

Proposition 2.4. Let k·k, k·k

′

, and k·k

′′

denote vector norms on R

, and R

, r espectively. Let k · k

′′′

be the matrix norm on R

m×l

induced

by k · k and k · k

′

, let k · k

′′′′

be the matrix norm on R

n×m

induced by k · k

′

and k · k

′′

, and let k · k

′′′′′

be th e matrix norm on R

n×l

induced by k · k and

k· k

′′

. If A ∈ R

n×m

and B ∈ R

m×l

, then

kABk

′′′′′

≤ kAk

′′′′

kBk

′′′

. (2.39)

Proof. Note that for all x ∈ R

and y ∈ R

, kBxk

′

≤ kBk

′′

kxk and

kAyk

′′

≤ kAk

′′′′

kyk

′

. Hence, for all x ∈ R

kABxk

′′

≤ kAk

′′′′

kBxk

′

≤ kAk

′′′′

kBk

′′′

kxk, (2.40)

which implies (2.39).

The following corollary to Proposition 2.4 is immediate.

Corollary 2.2. Every equi-induced matrix norm is a normalized

submultiplicative matrix norm.

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 21

2.3 Set Theory and Topology

The notion of a norm on R

discussed in the previous section provides the

basis for the development of some basic results in topology and analysis.

In this section, we restrict our attention to the Euclidean space R

. If X

is a set, then x ∈ X denotes that x is an element of X. The notation

x 6∈ X denotes that x is not an element of X. A set may be speciﬁed by

listing its elements such as S = {x

, x

} or, alternatively, a set may be

speciﬁed as consisting of all elements of set X having a certain property P .

In particular, S = {x ∈ X : P (x)}. The union of two sets is denoted by

X ∪ Y and consists of those elements that are in either X or Y. Hence,

X ∪ Y

△

= {x : x ∈ X or x ∈ Y} = Y ∪ X.

The intersection of two sets X and Y is denoted by X ∩ Y an d consists of

those elements that are common to both X and Y. Hence,

X ∩ Y = {x : x ∈ X, x ∈ Y}

= {x ∈ X, x ∈ Y}

= {x ∈ Y, x ∈ X}

= Y ∩ X.

The complement of a set X relative to another set Y is deﬁned by

Y \ X

△

= {x ∈ Y : x 6∈ X}, and consists of those elements of Y that are not

in X. When it is clear that the complement is with respect to a universal

set Y, that is, a ﬁ xed set from w hich we take elements and subs ets, then

we write X

∼

△

= Y \ X. If x ∈ X implies x ∈ Y, then X is contained in Y

or, equivalently, X is a s ubset of Y. In this case, we write X ⊆ Y. Clearly,

X = Y is equivalent to the validity of both X ⊆ Y and Y ⊆ X. If X ⊆ Y

and X 6= Y, then X is said to be a proper subset of Y, and is written as

X ⊂ Y. The set with no elements is called the empty set and is denoted

by Ø. Two sets X and Y are disjoint if their intersection is empty, that

is, X ∩ Y = Ø. Finally, a collection of pairwise disjoint subsets of a set X

whose union is equal to X is called a partition of X.

Example 2.4. Let X = (0, 3) and Y = [2, 4). Then X \ Y = (0, 2),

X ∪ Y = (0, 4), and X ∩ Y = [2, 3). With R as the universal set, Y

∼

(−∞, 2) ∪[4, ∞). Note that X ∩Y

∼

= (0, 3) ∩((−∞, 2) ∪[4, ∞)) = (0, 2) =

X \ Y. △

The Cartesian product X

×X

×···×X

of n sets X

, . . . , X

is the set

consisting of ordered elements of the form (x

, x

, . . . , x

), where x

∈ X

i = 1, . . . , n. Hence,

× ··· × X

= {(x

, . . . , x

) : x

∈ X

, . . . , x

∈ X

NonlinearBook10pt November 20, 2007

22 CHAPTER 2

We call x

∈ X

the ith element of the ordered set X

×···×X

. The deﬁnition

of the union, intersection, and product of sets can be extended from two

sets (or n sets in the case of products) to a ﬁnite or inﬁnite collection of sets

: i ∈ I}, where i runs over some set I of indices. We call {S

: i ∈ I}

an indexed family of sets. The deﬁnition of the union and intersection of a

collection of sets is

[

i∈I

△

= {x : x ∈ S

for at least one i ∈ I},

i∈I

△

= {x : x ∈ S

for every i ∈ I}.

If the collection is ﬁnite, the set of indices I is u s ually {1, . . . , n}, and if the

collection is countably inﬁnite I is usually Z

, although there are occasional

exceptions to this.

To begin let k·k be a norm on R

and d eﬁ ne the open ball B

(x) ⊂ R

with radius ε and center x by B

(x)

△

= {y ∈ R

: kx − yk < ε}. It is

important to note that B

(x) is not necessarily an open sphere or an open

ball; its shape will depen d on the norm chosen. For example, if x ∈ R

and

k · k = k · k

∞

, then B

(0), for which the point x is the origin (0,0), is the

interior of the square max{|y

|, |y

|} < 1.

Deﬁnition 2.9. Let S ⊆ R

. Then x ∈ S is an interior point of S if

there exists ε > 0 such that B

(x) ⊆ S. The interior of S is th e set

◦

△

= {x ∈ S : x is an interior point of S}.

Finally, the set S is open if every element of S is an interior point, that is,

if S =

◦

Note that

◦

⊆ S and every open ball is an open set.

Example 2.5. Let S

△

= {(x

, x

) ∈ R

: x

+ x

< 1}. S is an open

set in R

since given any x ∈ S, there exists ε > 0 s uch that B

(0) ⊆ S. △

Deﬁnition 2.10. Let x ∈ R

. A neig hborhood of x is an open subset

N ⊆ R

containing x.

In certain parts of the book we denote a neighborhood of x ∈ R

(x) to refer to B

(x) (or an ε-neighborhood of x).

Deﬁnition 2.11. Let S ⊆ R

. A vector x ∈ R

is a closure point of S

if, for every ε > 0, the set S ∩ B

(x) is not empty. A closure point of S is

an isolated point of S if there exists ε > 0 such that S ∩ B

(x) = {x}. The

NonlinearBook10pt November 20, 2007

DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS 23

closure of S is the set

△

= {x ∈ R

: x is a closure point of S}.

The set S is closed if every closure point of S is an element of S, that is,

S = S. Finally, the boundary of S is the set ∂S

△

= S\

◦

= S ∩ (R

\ S).

A closure point is sometimes referred to as an adherent point or contact

point in the literature. Note that

◦

⊆ S ⊆ S. A closure point should be

carefully distinguished from an accumulation point.

Deﬁnition 2.12. Let S ⊆ R

. A vector x ∈ R

is an accumulation

point of S if, for every ε > 0, the set S ∩(B

(x) \{x}) is not empty. The s et

of all accumulation points of S is called a derived set and is denoted by S

′

Note that if S ⊂ R

, then the vector x ∈ R

is an accumulation point

of S if and only if every open ball centered at x contains a point of S distinct

from x or, equivalently, every open ball centered at x contains an in ﬁnite

number of points of S. Note that if x is an accumulation point of S, then x

is a closure point of S. Clearly, for every S ⊂ R

, S = S ∪ S

′

, and hence S

is closed if and only if S

′

⊆ S. Thus, a set S ⊆ R

is closed if and only if it

contains all of its accumulation points. An accumulation point is sometimes

referred to as a cluster point or limit point in the literature.

Example 2.6. Let S ⊂ R be given by S = (0, 1]. Note that every point

α ∈ [0, 1] is an accumulation point of S since every open ball (open interval

on R in this case) containing α will contain points of (0, 1] distinct from α.

Note that the accumulation point 0 is not an element of S. Since 0 is the

only accumulation point that does not belong to S, the closure of S is given

by S = S ∪ S

′

= (0, 1] ∪ [0, 1] = (0, 1] ∪ {0} = [0, 1]. Finally, note that the

boundary of S is ∂S = S\

◦

= S ∩ (R

\ S) = [0, 1] ∩ ((−∞, 0] ∪ [1, ∞)) =

{0, 1}. △

Note that for a given set S ⊆ R

, closure points can be isolated points

of S, which always belong to S, accumulation points of S belonging to S,

and accumulation points of S which do not belong to S. For example, let

△

= {x ∈ R : 0 < x < 1, x = 2}. Clearly, x = 2 is an isolated closure point

of S, x = 0 and x = 1 are accumulation points, and hence, closure points of

S which do not belong to S, and every point x in the set {x ∈ R : 0 < x < 1}

is an accumulation point, and hence, a closure point of S belonging to S.

The next proposition shows that the complement of an open set is

closed and the complement of a closed set is open.

Proposition 2.5. Let S ⊆ R

. Then S is closed if and only if R

\ S

NonlinearBook10pt November 20, 2007

24 CHAPTER 2

is open.

Proof. S is closed if and only if, for every point x ∈ R

\ S, there

exists ε > 0 such that B

(x) ∩ S = Ø. This holds if and only if, for every

x ∈ R

\S, there exists an ε > 0 such that B

(x) ⊂ R

\S, which is true if

and only if R

\ S is open.

The empty set Ø and R

are the only subsets of R

that are both

open and closed. To see this, note that for every x ∈ R

, every open ball

(x) ⊂ R

. Hence, every point in R

is an interior point. Thus, R

open. Alternatively, note that Ø has no points, and hence, every point of Ø

is an interior point of Ø. Hence, Ø is an open subset of R

. Th e converse

follows immediately by noting that S ⊆ R

is closed if and only if R

\S is

open (see Proposition 2.5). Alternatively, R

is closed since it contains all

points, and hence, all accumulation points. The empty set is closed since it

has no accumulation points. Hence, ∂S = Ø if and only if S = Ø or S = R

Finally, note that s ince

∂S = [

◦

∪

◦

∼

)]

∼

∂S is always a closed set an d is given by the elements in R

that belong to

the set S but not

◦

Example 2.7. Let X = {(x

, x

) ∈ R×R : −1 < x

≤ 1, −1 < x

≤ 1}.

Note that X is neither open nor closed since the boundary point (x

, x

) =

(1, 1) is contained in X and the boundary point (x

, x

) = (−1, −1) is not in

X. The closure of X is X = {(x

, x

) ∈ R ×R : −1 ≤ x

≤ 1, −1 ≤ x

≤ 1},

whereas the interior is

◦

= {(x

, x

) ∈ R × R : −1 < x

< 1, −1 < x

< 1}.

The boundary of X is formed by the four segments {(x

, x

) ∈ R × R :

= 1, −1 ≤ x

≤ 1}, {(x

, x

) ∈ R × R : x

= −1, −1 ≤ x

≤ 1},

{(x

, x

) ∈ R × R : x

= 1, −1 ≤ x

≤ 1}, and {(x

, x

) ∈ R × R : x

−1, −1 ≤ x

≤ 1}, and hence, is given by the union of these four sets. △

Deﬁnition 2.13. Let S ⊆ R

. Then Q ⊆ S is dense in S if S ⊆ Q.

The set Q is nowhere dense in S if S\Q is dense in S.

Deﬁnition 2.13 implies that if Q is dense in S, then every element of

S is a closure point of Q, or an element of Q, or both. If S is closed, then

Q ⊆ S is dense if and only if Q = S. Note that the set of rational numbers

Q is a dense subset of R, whereas the set of integers Z is a nowhere dense

subset of R.

Deﬁnition 2.14. Let S ⊂ R

. Then S is bounded if there exists ε > 0

such that kx − yk < ε for all x, y ∈ S. Furthermore, S is compact if it is

closed and bou nded.