Гюннер Э.А., Шульгин В.Ф. Общая химия
Подождите немного. Документ загружается.


H
H
2
1/2H
2
(г) + 1/2I
2
(к)
1/2H
2
(г) + 1/2I
2
(г)
H
1
1/2H
2
(г) + I(г)
H(г) + I(г)
H
св
H
3
H
HI(г)
Рис. 52. Энтальпийная диаграмма образования HI из простых веществ
Как следует из рис. 51, тепловой эффект реакции (8-19)
ΔН = ΔН
1
+ ΔН
2
+ΔН
3
+ΔН
св
,
ΔН
св
= ΔН - ΔН
1
- ΔН
2
- ΔН
3
,
ΔН
св
= 26,3 – (31,2 + 74,7 + 216,1) = -295,7 кДж/моль
Соотвественно,
Е
св
= 295,7 кДж/моль
Тепловые эффекты реакций зависят от температуры. Рассмотрим математическое выражение этой
зависимости для случая, когда молярные теплоемкости реагирующих веществ и продуктов реакции при
постоянном давлении (С
р
) не зависят от температуры.
Пусть тепловой эффект реакции
aA + bB = dD + eE (8-20)
при температурах Т
1
и Т
2
равен ΔН
1
и ΔН
2
, а молярные теплоемкости веществ, участвующих во взаимодействии,
составляют С
р
(А), С
р
(В), С
р
(D) и С
р
(Е) кДж/мольК. Для решения задачи воспользуемся законом Гесса.
Осуществим реакцию (8-20) двумя путями:
1. Реакция (8-20) осуществляется одностадийно при температуре Т
1
с тепловым эффектом ΔН
1
.
2. Реакция (8-20) протекает по следующему пути:
а) реагенты А и В нагревают от температуры Т
1
до температуры Т
2
, чему соответствует тепловой эффект
ΔН
3
= (Т
2
- Т
1
)[aC
p
(A) + bC
p
(B)]
б) при температуре Т
2
проводят реакцию (8-20) с тепловым эффектом ΔН
2
;
в) охлаждают продукты реакции до температуры Т
1
; при этом
ΔН
4
= (T
1
- T
2
)[dC
p
(D) + eC
p
(E)]
Как следует из энтальпийной диаграммы (рис. 53)
ΔН
1
= ΔН
2
+ ΔН
3
+ ΔН
4
ΔН
2
= ΔН
1
-(Т
2
-Т
1
)[aC
p
(A) + bC
p
(B)] - (T
1
-T
2
)[dC
p
(D) + eC
p
(E)] =
= ΔН
1
+ (T
2
- T
1
){[dC
p
(D) + eC
p
(E)] - [aC
p
(A) + bC
p
(B)]}
В общем случае
ΔН
2
= ΔН
1
+ (Т
2
- Т
1
)[ Σn
i
C
p
(пр) - Σm
j
C
p
(реаг)] (8-21)
где n
i
и m
j
- соответствующие коэффициенты в уравнении реакции. Уравнение (8-21) было выведено К. С.
Кирхгоффом. Если рассматривать величину
1
T
2
T
1
ΔH
2
ΔH
как температурный коэффициент теплового эффекта,
закон Кирхгоффа можно сформулировать в следующем виде:
111

Температурный коэффициент теплового эффекта равен изменению теплоемкости системы,
происходящему в результате процесса.
H
aA + bB (T
2
)
aA + bB (T
1
)
dD + eE (T
1
)
dD + eE (T
2
)
H
4
H
3
H
2
H
1
Рис. 53. Зависимость теплового эффекта от температуры
В заключение отметим, что поскольку любая система стремится перейти в состояние, обладающее
минимальной энергией, протеканию реакции благоприятствуют отрицательные значения тепловых эффектов.
Однако отрицательные значения ΔН, как будет показано в разделе 8.2.4, не являются единственным критерием,
определяющим направление процесса.
8.2.3. Энтропия. Второй и третий законы термодинамики.
Термодинамические системы характеризуются различной степенью неупорядоченности. Так, например,
водяной пар менее упорядочен, чем лед; система, состоящая из воды и хлорида натрия в виде отдельных фаз,
более упорядочена, чем раствор, приготовленный из этих веществ. Для количественной характеристики
неупорядоченности системы в термодинамике используют специальную термодинамическую функцию -
энтропию (S). Чем больше энтропия системы, тем больше её неупорядоченность.
При переходе системы из одного состояния в другое энтропия может как повышаться, так и понижаться.
Примерами процессов, протекающих с повышением энтропии, могут служить плавление, кипение, диффузия,
растворение кристаллических веществ в жидкостях. Процессы, обратные рассмотренным, сопровождаются
понижением энтропии. Для химических реакций энтропия увеличивается, если процесс сопровождается
увеличением числа молекул газообразных соединений. В случае реакций, в которых участвуют только
кристаллические вещества, энтропия меняется незначительно. Рассмотрим, как можно количественно
охарактеризовать энтропию системы.
Состояние термодинамической системы можно задать двояко:
1) указав значения макропараметров системы - давления, объема, температуры, количества вещества;
состояние системы, заданное таким способом, называется макросостоянием;
2) указав значения параметров всех частиц, образующих систему - координат этих частиц, их импульсов и
энергий; состояние системы, заданное микропараметрами частиц, называется микросостоянием.
Совершенно очевидно, что каждому макросостоянию отвечает несколько (зачастую огромное число)
микросостояний.
Число микросостояний, позволяющих реализовать то или иное макросостояние, называется
термодинамической вероятностью данного состояния (W). Чем выше термодинамическая вероятность, тем чаще
система будет находиться в этом состоянии.
Пусть, например, система состоит из трех частиц, а для достижения данного макросостояния требуется,
чтобы одна из них имела скорость 10, другая - 20, а третья - 30 условных единиц. Ниже приведены все
возможные микросостояния, обеспечивающие это макросостояние:
Микросостояние v
1
v
2
v
3
1 10 20 30
2 10 30 20
3 20 10 30
4 20 30 10
5 30 10 20
6 30 20 10
Таким образом, термодинамическая вероятность данного макросостояния будет равна шести. Уменьшим
неупорядоченность системы, введя дополнительное ограничение: пусть при тех же значениях скоростей
скорость второй молекулы не может быть больше скорости третьей молекулы. В этом случае макросостояние
будут обеспечивать лишь микросостояния 1, 3 и 5; соответственно термодинамическая вероятность понизится
112

до трех. Таким образом, чем больше термодинамическая вероятность, тем выше неупорядоченность системы и,
следовательно, выше энтропия. Энтропия моля вещества связана с термодинамической вероятностью
уравнением Больцмана
S = RlnW, (8-22)
где R - универсальная газовая постоянная. Значение энтропии, равное 1 Дж/мольК, называется энтропийной
единицей (э.е.). Для одной частицы уравнение Больцмана имеет вид:
S = klnW, (8-23)
где k - постоянная Больцмана
A
N
R
k
=1,38
.
10
-23
Дж/К,
где N
A
- число Авогадро.
Как указывалось выше, то или иное состояние системы реализуется тем чаще, чем больше
термодинамическая вероятность этого состояния. Отсюда, учитывая уравнение (8-22), можно заключить, что чем
больше энтропия, тем больше вероятность перехода системы в состояние, отвечающее этой энтропии. Это
заключение выражает суть второго закона термодинамики:
Изолированная система самопроизвольно изменяется в направлении состояния, обладающего
максимальной термодинамической вероятностью и, следовательно, максимальной энтропией.
Часто используют и другую формулировку второго закона термодинамики:
Теплота не может самопроизвольно переходить от холодного тела к горячему.
Эти две формулировки взаимосвязаны и равноценны. Действительно, переход теплоты от холодного тела к
горячему сопровождается сосредоточиванием в одной части системы быстрых ("горячих") молекул, а в другой -
медленных ("холодных"); упорядоченность системы при этом возрастает, а термодинамическая вероятность и
энтропия понижаются. Согласно первой формулировке второго закона термодинамики такой процесс не может
протекать самопроизвольно, если система не обменивается с другими системами энергией. Таким образом,
процессы, идущие с понижением энтропии, в изолированной системе являются вынужденными.
Изменение энтропии системы при переходе из начального состояния в конечное
1
W
2
W
Rln
1
S
2
SΔS
, (8-24)
где W
1
и W
2
- термодинамические вероятности начального и конечного состояния системы.
На энтропию оказывают влияние следующие факторы:
1. Агрегатное состояние вещества. Фазовые переходы из кристаллического в жидкое, а затем в газообразное
состояние сопровождаются повышением энтропии.
2. Сложность структуры частиц. Усложнение структуры влечет за собой увеличение энтропии. Так, например,
для атомарного кислорода О, молекулярного кислорода О
2
и озона О
3
значения энтропии при стандартных
условиях составляют 161, 205 и 239 Дж/мольК. Это явление можно объяснить тем, что по мере усложнения
структуры молекул для последних становятся возможными новые формы движения частиц, что сопровождается
увеличением термодинамической вероятности состояния. Действительно, для атомарного кислорода частицы
могут отличаться лишь поступательным движением, тогда как для молекулярного кислорода и озона возможно
также вращательное и колебательное движение. При этом для угловых молекул озона набор разрешенных
колебательных и вращательных движений больше, чем для линейной молекулы кислорода.
3. Температура. Повышение температуры приводит к возрастанию энтропии в связи с увеличением средней
скорости движения молекул вещества. Если в температурном интервале Т
1
≤ Т ≤ Т
2
не наблюдается фазовых
переходов, изменение энтропии системы подчиняется уравнению
2
T
1
T
dT
T
p
C
ΔS
, (8-25)
где С
р
- молярная теплоемкость вещества. Для случая, когда С
р
- величина постоянная
1
T
2
T
ln
p
CΔS
(8-25а)
Как следует из уравнения (8-25а), с повышением температуры энтропия увеличивается.
Если температура системы постоянна, а процесс является равновесным, изменение энтропии связано с
тепловым эффектом процесса (ΔН) уравнением
T
ΔH
ΔS
(8-26)
Например, для фазовых переходов, являющихся равновесными изотермическими процессами,
ф.п.
T
ф.п.
ΔH
ΔS
где ΔН
ф.п.
и Т
ф.п.
тепловой эффект и температура фазового перехода. Если процесс не является равновесным, то
113

ΔS
>
T
ΔH
(8-26a)
4. Давление. С увеличением давления энтропия понижается, но незначительно, особенно в
конденсированных (твердых и жидких) системах. При повышении давления средние расстояния между
частицами уменьшаются, взаимодействие между ними усиливается, и система становится более упорядоченной.
В отличие от всех остальных термодинамических функций для энтропии могут быть определены абсолютные
значения этой характеристики, а не только ее изменение при переходе из одного состояния в другое. Пусть
какое-либо вещество находится при температуре абсолютного нуля. В такой системе движение частиц вещества
прекращается, и каждая частица имеет определенные, не изменяющиеся координаты. Подобному
макросостоянию отвечает одно единственное микросостояние, а термодинамическая вероятность состояния
равна единице, откуда
S
0
= RTln1 = 0
Рассмотренное явление позволяет сформулировать третий закон термодинамики:
При температуре абсолютного нуля энтропия идеального кристалла равна нулю.
Для реальных кристаллов энтропия при температуре 0 К может несколько отличаться от нуля. Это явление
можно объяснить наличием в таких кристаллах дефектов кристаллической решетки. Включения (атомы,
оказавшиеся в междоузлиях кристаллической решетки) и вакансии (незанятые места в кристаллической
решетке) повышают неупорядоченность структуры и, следовательно, энтропию системы. Однако и в
бездефектных кристаллах нулевая энтропия может быть выше нуля. Например, для кристаллического оксида
углерода(II) S
0
= 4,7 э.е. Отличие S
0
от нуля в данном случае можно объяснить тем, что молекулы СО в
кристалле могут сближаться как одинаковыми атомами (...СО…ОС…СО...), так и различными атомами (...СО…
СО…СО...). В результате термодинамическая вероятность состояния становится равной двум, откуда
S
0
= Rln2 = 5,7 Дж/моль
.
К,
что достаточно близко к наблюдаемой величине.
Третий закон термодинамики в сочетании с уравнениями (8-25) и (8-26) позволяет рассчитать энтропию
вещества при любой температуре. Пусть вещество с молярной теплоемкостью С
р
плавится при температуре Т
пл
и кипит при температуре Т
кип
; энтальпии плавления и парообразования для данного вещества равны ΔН
пл
и ΔН
пар
.
Определим энтропию этого вещества при температуре Т΄, превышающей температуру кипения. Изменение
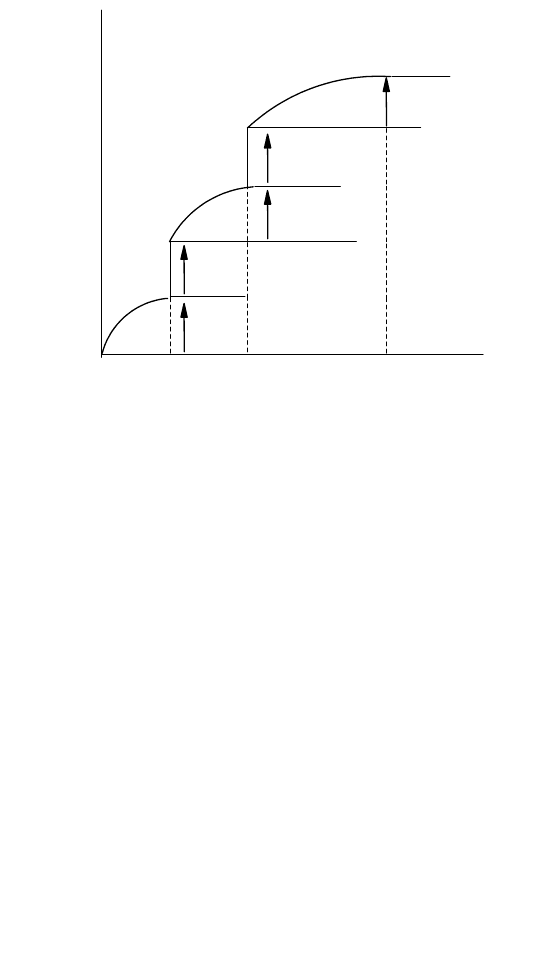
энтропии в интервале 0 Т΄ (ΔS΄) можно представить как сумму изменений энтропии, отвечающих
определенным температурным интервалам (рис. 54):
1) Т = 0; ΔS
0
в идеальном случае равно нулю, хотя может и несколько отличаться от нуля;
2) 0 < T < T
пл
;
пл
T
0
dT
T
p
C
1
ΔS
согласно уравнению (8-25);
3) Т = Т
пл
;
пл
T
пл
ΔH
пл
ΔS
в соответствии с уравнением (8-26);
4) Т
пл
< Т < Т
кип
;
кип
Т
пл
Т
dT
T
p
C
2
ΔS
5) Т = Т
кип
;
кип
T
пар
ΔH
пар
ΔS
6) Т
кип
< T ≤ Т΄;
T
кип
T
dT
T
p
C
3
ΔS
В результате энтропия вещества при температуре Т΄ составит
S΄ = ΔS
0
+ ΔS
1
+ ΔS
пл
+ ΔS
2
+ ΔS
пар
+ ΔS
3
114
Дж/моль К
S,
S
1
S
пл
S
2
S
пар
S
3
T
пл
T
кип
T' T
0
Рис. 54. Зависимость энтропии от температуры для вещества, существующего в
кристаллическом, жидком и газообразном состоянии (S
0
= 0)
Поскольку энтропия является функцией состояния, изменение энтропии при протекании химической реакции
aA + bB = dD + eE
может быть вычислено по уравнению
ΔS = [dS(D) + eS(E)] - [aS(A) + bS(B)]
или в общем виде
ΔS = Σn
i
S(пр) - Σm
j
S(реаг) (8-27)
В химической практике широко используют значения энтропии простых и сложных веществ, отнесенные к
стандартным условиям. Эти величины называются стандартными энтропиями (Δ
298
S
); они приводятся в
справочниках термодинамических свойств и используются при разнообразных термодинамических расчетах.
В качестве примера рассчитаем изменение энтропии, отвечающее синтезу карбоната кальция и силиката
кальция из оксидов:
1) СаО(к) + СО
2
(г) = СаСО
3
(к)
Δ
298
S
=
298
S
(СаСО
3
) - [
298
S
(CаО) +
298
S
(СО
2
)] =
= 91,7 - (38,1 + 213,7) = -160,1 Дж/мольК
2) СаО(к) + SiO
2
(к) = СаSiO
3
(к)
Δ
298
S
=
298
S
(CaSiO
3
) - [
298
S
(CaO) +
298
S
(SiO
2
)] =
= 81,0 - (38,1 + 41,2) = 1,7 Дж/мольК
Как и следовало ожидать, реакция образования карбоната кальция, при которой имеет место связывание
газообразного вещества (СО
2
), сопровождается существенным уменьшением энтропии системы, а при синтезе
силиката кальция из кристаллических оксидов энтропия почти не изменяется.
8.2.4. Свободная энергия Гиббса. Направление химического процесса.
Одной из важнейших задач, решаемых термодинамикой, является установление принципиальной
возможности (или невозможности) самопроизвольного протекания химического процесса.
Как указывалось в разделе 8.2.2, протеканию химического процесса благоприятствует повышение энтропии
системы. Повышение энтропии достигается разобщением частиц, разрывом химических связей, разрушением
кристаллических решеток, растворением одних веществ в других и т.д. Однако все эти процессы неизбежно
сопровождаются повышением энтальпии системы, что препятствует протеканию процесса (см. раздел 8.2.3).
Таким образом, все процессы, благоприятствующие переходу системы из начального состояния в конечное за
счет возрастания энтропии, не благоприятствуют такому переходу в связи с повышением энтальпии системы.
Очевидно, что для решения вопроса о принципиальной возможности протекания химического процесса
необходимо одновременно учесть изменение и энтропии, и энтальпии системы. При постоянных температуре и
давлении для этой цели используется термодинамическая функция, называемая свободной энергией Гиббса
(иногда просто энергией Гиббса). Свободная энергия Гиббса (G) cвязана с энтальпией и энтропией уравнением
115

G = H - TS (8-28)
Изменение энергии Гиббса при переходе системы из начального состояния в конечное определяется
соотношением
ΔG = ΔH - TΔS (8-29)
Поскольку уравнение (8-29) справедливо для процессов, протекающих при постоянных температуре и
давлении, функцию G называют также изобарно-изотермическим потенциалом. В уравнении (8-29) величина ΔН
оценивает влияние на возможность протекания процесса энтальпийного фактора, а величина ТΔS -
энтропийного фактора. По своему физическому смыслу свободная энергия Гиббса - это та часть ΔН, которая при
определенных условиях может быть превращена в работу, совершаемую системой против внешних сил.
Остальная часть ΔН, равная ТΔS, представляет "несвободную" энергию, которая идет на повышение энтропии
системы и в работу превращена быть не может. Свободная энергия Гиббса - это своеобразный химический
потенциал, определяющий движущую силу химического процесса. Подобно физическим потенциалам
(электрическому, гравитационному) энергия Гиббса уменьшается по мере самопроизвольного протекания
процесса до тех пор, пока не достигнет минимального значения, после чего процесс прекратится.
Пусть в системе при постоянных давлении и температуре cамопроизвольно протекает какая-то реакция
(неравновесный процесс). В этом случае в соответствии с уравнением (8-26а)
ΔH < TΔS
и, следовательно,
ΔG < 0
Таким образом, изменение функции Гиббса может служить критерием при определении направления
протекания реакций:
В изолированной или закрытой системе при постоянных температуре и давлении самопроизвольно
протекают реакции (прямые или обратные), для которых изменение свободной энергии Гиббса
отрицательно (ΔG < 0).
Пусть протекающая в системе реакция обратима. Тогда при заданных условиях прямая реакция
принципиально осуществима, если ΔG < 0, а обратная - если ΔG > 0; при ΔG = 0 система будет находиться в
состоянии равновесия (см. раздел 8.4.1).
Для изолированных систем ΔН = 0, откуда в соответствии с (8-29)
ΔG = - TΔS (8-30)
Таким образом, в изолированной системе самопроизвольно протекаю процессы, приводящие к повышению
энтропии этой системы (второй закон термодинамики).
Поскольку в уравнение (8-28) входит энтальпия системы, определить значение энергии Гиббса невозможно.
Для расчета изменения свободной энергии, отвечающего протеканию той или иной реакции, используют энергии
Гиббса образования соединений, участвующих во взаимодействии.
Энергия Гиббса образования соединения (ΔG
f
) - это изменение свободной энергии, соответствующее
синтезу моля данного соединения из простых веществ. Энергии Гиббса образования соединений, отнесенные
к стандартным условиям, называются стандартными и обозначаются символом ΔG
f,298
.
Значения ΔG
f,298
приведены в справочной литературе; их можно также вычислить по значениям энтальпий
образования и энтропий соответствующих веществ. Пусть, например, требуется рассчитать ΔG
f,298
для Fe
3
O
4
,
если известна энтальпия образования этого соединения (ΔН
f,298
(Fe
3
O
4
) = -1117,13 кДж/моль) и энтропии ΔS
298
железа, кислорода и Fe
3
O
4
, равные 27,15, 205,04 и 146,19 Дж/моль
.
К. Согласно (8-29)
ΔG
f,298
(Fe
3
O
4
) = ΔH
f,298
(Fe
3
O
4
) - T ΔS
298
где ΔS
298
- изменение энтропии при протекании реакции
3Fe + 2O
2
= Fe
3
O
4
(8-31)
В соответствии с (8-27)
ΔS
298
= S
298
(Fe
3
O
4
) - [3S
298
(Fe) + 2S
298
(O
2
)] =
=146,19 - (3
.
27,15 + 2
.
205,04) = -345,34 Дж/моль
.
К =
= -0,34534 кДж/моль
.
К
Тогда
ΔG
f,298
(Fe
3
O
4
) = -1117,13 - 298(-0,34534) =-1014,2 кДж/моль
.
К
Полученный результат позволяет заключить, что реакция (8-31) принципиально возможна при стандартных
условиях. В данном случае энтальпийный фактор благоприятствует протеканию реакции (ΔН
f,298
< 0), а
энтропийный - препятствует (ТΔS
298
< 0), но не может увеличить ΔG
f,298
до положительной величины
116

Поскольку G является функцией состояния, для реакции
aA + bB = dD + eE
изменение энергии Гиббса можно определить по уравнению
ΔΣ = Σn
i
ΔG
f
(пр) - Σm
j
ΔG
f
(реаг) (8-32)
В качестве примера оценим принципиальную возможность получения озона при взаимодействии азотной
кислоты с кислородом (условия стандартные) по уравнению:
4HNO
3
(ж) + 5O
2
(г) = 4O
3
(г) + 4NO
2
(г) +2H
2
O(ж) (8-33)
Как следует из (8-32),
ΔG
298
= [4ΔG
f,298
(O
3
) + 4ΔG
f,298
(NO
2
) + 2ΔG
f,298
(H
2
O)] -
- [4ΔG
f,298
(HNO
3
) + 5ΔG
f,298
(O
2
)] =
= 4
.
162,78 + 4
.
52,29 - [4(-79,90) + 5
.
0] = 1179,82 кДж/моль
.
К
Самопроизвольное протекание реакции (8-33) при стандартных условиях принципиально невозможно. В то
же время диоксид азота может быть окислен озоном до азотной кислоты, так как для обратной реакции значение
ΔG отрицательно.
Одним из факторов, существенно влияющих на направление реакции, является температура. Изменение
температуры влияет как на энтальпийный член (закон Кирхгоффа), так и на энтропийный член уравнения (8-29).
Однако влияние температуры на энтропийную составляющую больше, чем на энтальпийную, так как
температура в выражении ТΔS является сомножителем. По этой причине при очень низких температурах
энтропийный член ТΔS стремится к нулю, и направление процесса определяется энтальпийным членом ΔН
(самопроизвольно протекают экзотермические реакции). При достаточно высоких температурах ΔН < TΔS; в
этих условиях самопроизвольно протекают реакции, идущие с повышением энтропии вне зависимости от знака
теплового эффекта. При очень высоких температурах все вещества разлагаются на атомы, не способные
соединятся друг с другом, и химическая форма движения материи становится невозможной. В соответствии со
сказанным при анализе влияния температуры на направление реакции можно пренебречь влиянием
температуры на ΔН и ограничиться анализом влияния температуры на энтропийный член уравнения (8-29).
Пусть для данной реакции ΔS > 0. В этом случае повышение температуры будет сопровождаться
уменьшением алгебраического значения ΔG и, следовательно, благоприятствовать протеканию прямой реакции.
Если для данного процесса ΔS < 0, то с повышением температуры алгебраическое значение ΔG будет
возрастать, благоприятствуя осуществлению обратной реакции. Например, при взаимодействии ртути с
кислородом по уравнению
Hg(ж) +
2
1
O
2
(г) = HgO(к);
(ΔH
298
=-90,28; кДж/моль; ΔS
298
= -43,58 Дж/моль
.
К) и тепловой эффект, и изменение энтропии при
стандартных условиях отрицательны. Следовательно, повышение температуры должно благоприятствовать
протеканию обратной реакции, а понижение температуры - прямой. Действительно, как следует из рис. 55, при Т
< 750 K в системе протекает прямая реакция, для которой в этих условиях значения ΔG отрицательны; при Т >
750 К оксид ртути самопроизвольно разлагается на ртуть и кислород.
В заключение еще раз подчеркнем, что термодинамика позволяет установить лишь принципиальную
возможность протекания реакции, но не отвечает на вопрос, будет ли реакция осуществляться в данных
условиях реально. Так, для реакции
Н
2
(г) +
2
1
О
2
(г) = Н
2
О(г)
ΔG
298
= -228,61 кДж/моль. Однако при стандартных условиях смесь водорода и кислорода может существовать
тысячелетия без образования сколько-нибудь заметных количеств воды.
117

пря мая
реакция
обратнаяя
реакция
G
G > 0
G = 0
G < 0
750
T, K
Рис. 55. Влияние температуры на направление реакции Hg(ж) + ½O
2
(г) = HgO(к)
Таким образом, термодинамика изучает лишь изменение системы при переходе из одного состояния в
другое, но не пути, по которым может осуществляться такой переход. Вопрос о реальной возможности перехода
системы из одного состояния в другое изучает второй раздел теории химических процессов - химическая
кинетика.
8. Химическая кинетика
8.3.1. Предмет химической кинетики. Скорость химической реакции.
Энергия активации.
Химическая кинетика - это раздел теории химических процессов, изучающий механизмы протекания и
скорости химичеcких реакций. В отличие от химической термодинамики, изучающей состояние системы вне
зависимости от того, как это состояние возникло, химическая кинетика имеет предметом изучения конкретные
пути перехода из одного состояния в другое, т.е. возможность реализации процесса и его развитие во времени.
Под механизмом реакции понимают последовательность элементарных (одностадийных) реакций,
приводящих к экспериментально наблюдаемым реакции и ее кинетике.
Скорость химической реакции - это число актов химического взаимодействия за единицу времени в
единице реакционного пространства.
Химические реакции могут быть подразделены на гомогенные и гетерогенные. Гомогенные реакции
протекают во всем объеме фазы (например, взаимодействие азота с водородом в газовой фазе или реакция
между гидроксидом натрия и азотной кислотой в растворе). Гетерогенные реакции протекают на поверхности
раздела фаз (например, взаимодействие оксида магния с азотной кислотой в растворе). Для гомогенных реакций
единицей реакционного пространства следует считать единицу объема, для гетерогенных - единицу поверхности
раздела фаз. Поскольку число актов взаимодействия пропорционально количеству прореагировавшего или
образовавшегося вещества в единице реакционного пространства, средняя скорость реакции за отрезок времени
12
ττΔτ
выразится уравнением
X
1
Δτ
Δn
v
ср
, (8-34)
где ∆n = n
2
- n
1
- изменение количества вещества, по которому измеряется скорость, за время ∆, Х - объем
фазы или поверхность раздела фаз. Знак "плюс" в уравнении (8-34) отвечает случаю, когда выбранное вещество
является продуктом реакции и ∆n > 0; знак "минус" соответствует случаю, когда вещество в процессе реакции
расходуется и ∆n < 0. Для гомогенных реакций выражение (8-34) принимает вид
V
1
Δτ
Δn
v
ср
или, поскольку
V
Δn
- изменение концентрации вещества в молях на литр (С),
Δτ
ΔC
v
ср
В процессе реакции концентрации веществ изменяются, следовательно, меняется и скорость. Скорость реакции
в данный момент времени (истинная скорость) определяется первой производной концентрации по времени
118

dτ
dC
)
Δτ
ΔC
lim(v
(8-35)
Δ→0
Уравнение (8-35) часто используют и для гетерогенных реакций, если для данного отрезка времени поверхность
раздела фаз можно считать постоянной. В этом случае о скорости реакции судят по изменению концентрации
одного из веществ, находящихся в газовой фазе или в растворе. Например, о скорости реакции растворения
цинка в серной кислоте (гетерогенная реакция) можно судить по изменению концентрации ионов водорода в
жидкой фазе.
Пусть вещество А превращается в вещество В по уравнению
А → В (8-36)
Если вещество А стабильно, то образование его на конечной стадии обязательно должно было
сопровождаться понижением энергии Гиббса независимо от того, является ли реакция синтеза А
экзотермической или эндотермической. В противном случае вещество А просто не смогло бы образоваться.
Поэтому вещество А не может непосредственно превратиться в вещество В, даже если для реакции (8-36) ΔG <
0. Веществу А необходимо предварительно сообщить некоторую энергию, чтобы вывести его из устойчивого
состояния, так как только тогда станет возможным превращение его в вещество В. Таким образом, путь реакции
всегда включает три состояния: исходные вещества (реагенты), переходное или активированное состояние и
продукты реакции.
Минимальное количество энергии, которое необходимо сообщить системе, чтобы взаимодействие
стало возможным, называется энергией активации (Е
а
, кДж/моль).
Один из путей, по которому могла бы протекать термодинамически разрешенная реакция, включает
расщепление молекул реагентов на отдельные атомы и синтез из последних продуктов реакции. Однако этот
путь обычно не реализуется, так как ему отвечает очень высокая энергия активации. Для большинства
процессов промежуточной стадией является образование так называемого активированного комплекса.
Активированный комплекс - это ассоциат частиц, участвующих в химической реакции, в котором
синхронно происходит разрыв старых и образование новых связей.
Активированный комплекс нельзя рассматривать как неустойчивое соединение, так как основные
характеристики вещества (межъядерные расстояния, валентные углы и т.д.) к нему неприменимы. Время
существования активированного комплекса очень мало (10
-12
- 10
-13
с).
Протекание реакций изображают с помощью кинетических диаграмм. При построении таких диаграмм по
абсциссе откладывают путь реакции, указывая, как процесс развивается во времени, а по ординате - значения
энтальпии системы. Подобная диаграмма приведена на рис. 56. Вещества А и В превращаются в соединение АВ
с тепловым эффектом процесса ΔН; при этом исходные вещества, поглощая энергию Е
а
(пр), переходят в
состояние активированного комплекса АВ, который затем с выделением энергии превращается в продукт
реакции АВ. На рис. 56 показана также энергия активации обратной реакции (Е
а
(обр)). Из рис. 56 следует, что:
1) тепловой эффект реакции не зависит от энергии активации;
2) тепловой эффект реакции равен разности энергий активации прямой и обратной реакции
ΔН = Е
а
(пр) - Е
а
(обр) (8-37)
3) энергия активации - это тепловой эффект процесса образования активированного комплекса из реагирующих
веществ.
Если реакция протекает в несколько стадий, то каждой из этих стадий соответствует свой активированный
комплекс и своя энергия активации. Промежуточные продукты, при этом образующиеся, называются
интермедиатами.
A + B
AB
A B
...
Е
а
(пр)
Е
а
(обр)
Н
Н
путь реакции
Рис. 56. Кинетическая диаграмма реакции А + В = АВ.
Н –тепловой эффект реакции,
119
Е
а
(пр) – энергия активации прямой реакции,
Е
а
(обр) – энергия активации обратной реакции,
АВ – активированный комплекс
В качестве конкретного примера рассмотрим кинетику реакции
H
2
(г) + I
2
(г) = 2HI(г); ΔН = -10,2 кДж/моль (8-38)
кинетическая диаграмма которой приведена на рис. 57.
Н
H
2
(г) + I
2
(г)
I I
...
I H
2
I
...
...
2I
2HI(г)
E
a
(1)
E
a
(2)
Н
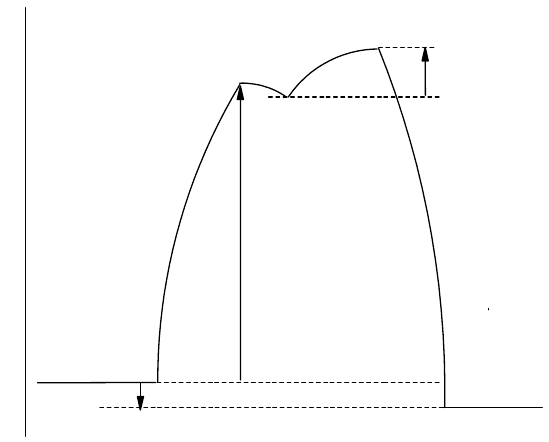
Рис. 57. Кинетическая диаграмма реакции H
2
(г) + I
2
(г) = 2HI(г)
Эта реакция протекает в две стадии, каждая из которых характеризуется определенной энергией активации.
На первой стадии молекула иода поглощает энергию, переходя в состояние активированного комплекса II,
который затем распадается на атомы иода
I
2
= II = 2I; E
a
(1) = 149 кДж/моль (8-39)
На второй стадии взаимодействия атомарный иод образует активированный комплекс с молекулой водорода,
превращающийся затем в иодоводород
2I + H
2
= IH
2
I = 2HI; E
a
(2) = 18 кДж/моль (8-40)
Интермедиатом в этой реакции является атомарный иод. Если рассматриваемую реакцию осуществить,
расщепляя на атомы и иод, и водород, а затем синтезируя из этих атомов иодоводород, энергия активации
составила бы 581 кДж/моль, что значительно превышает сумму Е
а
(1) и Е
а
(2), равную 167 кДж/моль. Таким
образом, второй путь энергетически невыгоден и не будет реализован.
8.3.2. Факторы, влияющие на скорость химической реакции.
Катализаторы и катализ.
Важнейшими факторами, влияющими на скорость химической реакции, являются концентрация реагентов,
температура, энергия активации, энтропия активации и катализаторы. Остановимся на характеристике каждого
из этих факторов.
1. Влияние концентрации
Химические реакции можно подразделить на реакции соударения, требующие для своего осуществления
столкновения двух или нескольких частиц (одинаковых или разных), и реакции возбуждения, в случае которых
молекула поглощает энергию, переходит в возбужденное состояние, а затем разрушается, образуя продукты
реакции. Так, реакция (8-40) будет реакцией столкновения, а реакция (8-39) - реакцией возбуждения. Для обеих
групп реакций повышение концентрации реагирующих веществ вызовет увеличение скорости реакции в
результате увеличения абсолютного числа результативных столкновений или актов перехода молекул в
возбужденное состояние, хотя отношение результативных столкновений к общему числу столкновений, как и
доля активированных молекул от их общего числа, не изменится. Количественно зависимости скорости реакции
от концентрации определяется законом действия масс (К. Гульдберг, П. Вааге, 1879):
Для одностадийных реакций при постоянной температуре скорость реакции прямо пропорциональна
произведению концентраций реагирующих веществ.
Так, для одностадийной реакции
120
