Гусак А.А., Бричикова Е.А. Теория вероятностей. Справочное пособие к решению задач
Подождите немного. Документ загружается.


Реш
е
н
и
е.
Найдем
сначала
закон
распределения
данной
дискретной
случайной
величины
Х.
эта
величина
может
принимать
три
значения:
х(=О, Х2=1,
хз=2.
Введем
обозначения:
событие
А(
-
"попадание
первого
стрелка",
со
бытие
А
2
-
"попадание
второго
стрелка",
тогда
А
1
и
~
-
их
промахи
соответственно.
Из
условия
задачи
следует,
что
q1
=
Р(А
,
)
=
1-
Р1
= 0,5,
q2
=Р(А
2
)=1-Р2
=0,6.
Значению
х(=О
соответствует
случай,
когда
у
обоих
стрелков
про-
махи
-
произошло
событие
А
=
Л;~,
где
А
1
и
А
2
-
независимые
собы-
тия,
поскольку
А
1
И
А
2
независимы.
По
теореме
умножения
получаем
Р(А)
=
P(~)·P(A2)
=
0,5
·0,6 = 0,3.
Значению
Х2=
1
соответствует
-случай,
когда
число
попаданий
равно
единице:
попадание
у
первого
стрелка
и
промах
у
второго
или
попада
ние
у
второго
и
промах
у
первого.
Это
значит,
что
произошло
собыtие
В
=
А
1
А
2
+
А
2
А
1
'
где
А
1
А
2
и
А
2
А
1
-
несовместные
события,
А
1
и
А
2
,
А
2
И
А
1
-
независи
мые
события
соответственно.
На
основании
теорем
сложения
и
умноже
ния
находим:
р(в)
=
Р(А
1
А
2
)+
P(AzA\)
=
P(A1)P(~)+P(Az)P(A1)
=
= 0,5·0,6 + 0,4·0,5 =
0,3
+ 0,2 = 0,5.
Значению
хз=2
соответствует
случай,
когда у
обоих
стрелков
попа
дания:
произошло
событие
С
=
А,
А
2
•
Следовательно,
Р(С)
=
Р(А
1
А
2
)
=
Р(А,
)Р(А
2
)
=
0,5·0,4
= 0,2.
Таким
образом,
закон
распределения
данной
случайной
величины
можно
задать
таблицей
х
О
2
Р
0,3
0,5
0,2
Построим
функцию
распределения
этой
случайной
величины.
На
основании
формулы
(2.2.11)
получим:
10]
1.
При
х
~
О
F(x)
=
L,P(X
=xk)=O.
xk<O
2.
При
О
<х
~
1
F(x)
=
L,P(X
=x/r)
=Р(Х
=
О)
=
0,3.
Xk<l
3.
При
1 <
х ~
2
F(x)
=
L,P(X
=x/r)
=Р(Х
=
О)+Р(Х
=
1)
=
4.
При
х
> 2
у
0,8
Xk<2
= 0,3 + 0,5 = 0,8.
F(x)
=Р(Х
=
О)+Р(Х
=
l)+P(X
= 2) =
=
0,3+0,5+0,2
=
1.
0>--------
0-----
0,30-----
О
2 3
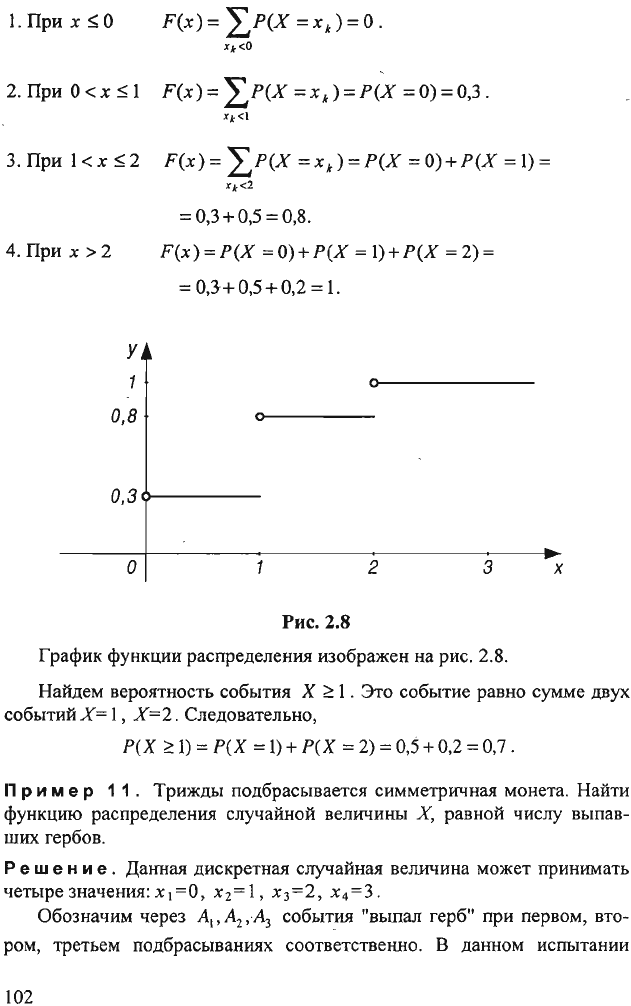
Рис.
2.8
График
функции
распределения
изображен
на
рис.
2.8.
х
Найдем
вероятность
события
Х
;:::
1 .
Это
событие
равно
сумме
двух
событий
Х=
1,
Х=2.
Следовательно,
Р(Х
;:::
1)
=
Р(Х
=
1)
+
Р(Х
= 2) = 0,5 + 0,2 = 0,7 .
11
Р
и
м
е р
1
1.
Трижды
подбрасывается
симметричная
монета.
Найти
функцию
распределения
случайной
величины
Х,
равной
числу
выпав
ших
гербов.
Реш
е н и
е.
Данная
дискретная
случайная
величина
может
принимать
четыре
значения:
Х
1
=0,
Xz=
1,
ХЗ
=2,
Х4
=3.
Обозначим
через
А
1
,
A
z
,Аз
события
"вьшал
герб"
при
первом,
вто-
ром,
третьем
подбрасываниях
соответственно.
В
данном
испытании
102

8
элементарных
исходов:
А
1
А
2
А
з
,
А
1
А
2
А
з
,
А)А
2
А
з
,
А)А
2
А
з
,
А)А
2
А
з
,
- -
А
1
А
2
А
з
,
А)А
2
А
з
,
А)А
2
А
з
·
У~итывая
независимость.
событий
А),
А
2
,
Аз
и
противоположных
им
событий
Л;,
А
2
,
Аз,
что
вероятность
появления
герба
при
одном
подбрасывании
равна
112,
находим
соответствующие
вероятности:
--
- - - - 1
Р(Х
=0)
=
Р(А)А
2
А
з
)
=
Р(А
1
)Р(А
2
)Р(А
з
)
=-,
8
1
Р(Х
= 3) =
Р(А)А
2
А
з
)
=
Р(А)Р(А
2
)Р(А
з
)
=
-.
8
Итак,
закон
распределения
рассматриваемой
дискретной
случайной
величины
Х
может
быть
представлен
следующей
таблицей:
х
о
2
3
р
118
3/8 3/8
118
в
соответствии
с
формулой
(2.2.11)
находим
функцию
распределе-
ния
О
nрих
~
О,
1/8
при
О
<
х
~
1,
F(x)=
1/2
при
I
<х
~2,
7/8
при
2 <
х
~
3,
1
nрих
>3.
Задачи
Является
ли
функцией
распределения
некоторой случайной
величи
ны
каждая
из
следующих
функций:
1.
F(x)
=
{:-~
при
х
~O,
при
х
>0.
103

3.
F(X
J
={:'
при
х ~O,
при
х>О.
при
х ~O,
при
0<
х
~
1,
nрих>1.
{
О
при
х
~
О,
4.
F(x)
= cos
х
при
О
<
х
~
n12,
1
при
х
> rc/2.
5.
Случайная
величина
Х
задана
функцией
распределения
1
0
при
x~O.
F(x)=
х/4
npиO<x~4,
1
при
х
> 4.
Найдите
вероятность
того,
что
в
реЗУЛЬ11lте
испытания
случайная
величина
примет
значение
из
интервала
(2,4).
6.
Случайная
величина
Х
задана
функцией
распределения
1
0
при
x~O,
F(x)=
х
npuO<x~l.
1
nрих>1.
Найти
вероятность
того,
что
в
результате
испытания
случайная
ве
личина
примет
значение
из
интервала
(5, 6).
7.
Закон
распределения
дискретной
случайной
величины
Х
задан
таблицей
х
6 8
12
15
р
0,1
3120
0,5 0,25
Найдите
функцию
распределения
этой
случайной
.величины.
Найди
те
вероятность
того,
что
6 <
Х
~
12 .
8.
Подбрасываются
две
монеты.
Случайная
величина
Х
-
число
вы
падений
герба
на
верхних
сторонах
монеты.
Найдите
функцию
распре
деления
случайной
величины
Х.
Постройте
график
этой
функции.
9.
Из
25
контрольных
работ,
среди
которых
5
оценены
на
"отлично",
наугад
извлекают
3
работы.
Найдите
функцию
распределения
дискрет-
104

ной
случайной
величины
Х,
равной
числу
оцененных
на
"отлично"
работ
среди
извлеченных.
Используя
функцию
распределения
найдите
вероят
ность
события
1
~
Х
~
2 .
10.
Подбрасываются
три
игральных
кубика.
Найдите
функцию
рас
пределения
случаЙНQЙ
величины
Х,
равной
сумме
очков
на
верхних
гра
нях
всех
кубиков.
Ответы
1.
Да.
2.
Нет.
3.
Да.
4.
Нет.
5.
S.
6.
О.
10.
У
к
а
з
а
н
и
е
.
См.
Указание
к
зада-
че7
§ 2.1.
Вопросы
1.
Как
определяется
функция
распределения
случайной
величины
х?
2.
Какие
другие
названия
используют
для
функции
распределения?
3.
Как
с
помощью
функции
распределения
F(x)
вычислить
вероят
ность
того,
что
случайная
величина
Х
примет
значение
из
полу
интервала
[а,
~)?
4.
Какую
случайную
величину
называют
непрерывной?
5.
Какими
свойствами
обладает
функция
распределения
случайной
величиныХ?
6.
Какой
вид
имеет
график
функции
распределения?
7.
Чему
равна
вероятность
того,
что
непрерьmная
случайная
величи
на
Х
примет
одно,
заданное
определенное
значение?
8.
Можно
ли
утверждать,
что
событие
А
является
невозможным,
ес
ли
Р(А)
=о?
9.
Как
определяется
функция
распределения
для
дискретной
случай
ной
величины?
10.
Является
ли
непрерывной
функция
распределения
для
дискрет
нОй
случайной
величины?
§ 2.3.
Плотность
распределения
Плотностью
расnределения
l
вероятностей
случайной
величицы
Х
в
точке
х
называется
предел
отношения
вероятности
попадания
значений
этой
величины
в
интервал
(х,
x+d
х)
к
длине
d
х
отрезка
[х,
x+d
х],
когда
последняя стремится
к
нулю:
()
1
.
Р(х
<
Х
<
х
+ d
х)
р
х =
1т
.
6 ...... 0 d
х
(2.3.1)
1
Плотность
рас~ределения
называют
также
дифференциШ1ЬНОЙ
ФУНК
цией
распределения.
105

График
функции
р{х)
(плотности
распределения)
называется
кри
вой
распределения.
Интеграл
от
функции.
р{х)
по
промежутку
(-
00,
х)
равен
значению
функции
распределения
F{x)
для
верхнего
предела
интегрирования,
Т.е.
х
f
p{t)dt
=
F{x)
.
(2.3.2)
Вероятность
попадания
значений
случайной
величины
Х
в
интервал
(а.,13)
равна
определенному
интегралу
от
плотности
распределения
р{х)
по
отрезку
[а.,
13],
Т.е.
р
Р{а.
<
Х
<
13)
= f
р{х)ш.
(2.3.3)
а
ПЛотность
распределения
обладает
следующими
свойствами.
1.
ПЛотность
распределения
р(х)
-
неотрицательная
функция,
Т.е.
р{х)
~
О.
(2.3.4)
Это
следует
из
определения
(2.3.1)
и
свойств
вероятности.
2.
В
точках
дифференцируемости
функции
распределения
F{x)
ее
производная
равна
плотности
распределения:
F'
(х)
=
р(х)
(2.3.5)
(производная
интегральной
функции
равна
дифференциальной
функции).
3.
Интеграл
по
бесконечному
промежутку
(-
00,
+
00)
от
плотности
распределения
р{х)
равен
единице:
+~
f
р{х)ш
= 1.
(2.3.6)
Если
все
возможные
значения
случайной
величины
принадлежат
от
резку
[а.,
13]
,
то
-
р
f
р(х)ш
= 1,
(2.3.7)
а
так
как
р{х)
=
О вне
этого
отрезка.
11
р и
м
е р
1.
Плотность
распределения
случайной
величины
Х
задана
функцией
106

с
Р(Х)=--2
.
l+х
Найти
значение
параметра
е.
Ре
w
е
н
и
е.
ПЛотность
распределения
должна
удовлетворять
условию
(2.3.6),
Т.е.
должно
выполняться
равенство
+f-
С
+f-
dx
--dx=c
--=1
1+х
2
1+х
2
'
откуда
1
+-
с=}
f~.
l+х
Неопределенный
интеграл
является
табличным:
f
~=arctg
х.
l+x
Вычислим
несобственный
интеграл:
+00
О
+-
f
dx f dx f dx
10
1+-
--2
=
--2
+
--2
=aretgx
+aretgx
=
l+x
l+x
ol+x
~
о
1t 1t
=
аге
tg
0-
аге
tg
(-
00)+
аге
tg (+
00)-
аге
tg
О
=
О
-(--)+--
0=
п.
2 2
Следовательно,
е
= 1/ 1t ;
плотность
распределения
имеет
вид
При
м
е р
2.
Плотность
вероятности
случайной
величины
Х
задана
функцией
j
O
npи~
::;
О,
р(х)=
х/2
nриО<х
::;2,
О
nрих
>
2.
Найти
вероятность
того,
что
в
результате
испытания
величина
Х
примет
значение
из
интервала
(1, 2).
Ре
w
е
н
и
е.
Искомую
вероятность
найдем
по
формуле
(2.3.3):
107

2
Х
х212
22
12
1 3
P(l<X
<2)=f-dx=-
=---=1--=-=075.
2
4144
44'
1
При
м
е
р
з.
Функция
распределения
случайной
величина
Х
имеет
вид
при
Х ~
О,
F(x)=f~
ll+x
2
Найти
ее
плотность
распределения.
при
х
>
о.
Реш
е
н
и
е.
Плотность
распределения
р(х)
и
функция
распределения
F(x)
связаны
соотношением
(2.3.5).
в
соответствии
с
равенством
(2.3.5)
находим:
р(х)
=
F'
(х)
=
о
при
х
~
о.
Итак,
плотность
распределения
вероятностей
данной
случайной
ве
личины
определяется
функцией
при
Х ~o,
при
х
>
о.
3
а
м
е
ч
а
н и
е.
эта
функция
удовлетворяет
условиям
(2.3.4)
и
(2.3.6).
Дей
ствительно,
+~
о
+~
+~
. I
2х
.
d(x
2
+1) 1
+~
f
р(х)ш=
f
Ош+
f 2 2
=0+
f 2 2
=---2
=-(0-1)=1.
(l
+
х
)
(1
+
х
) 1 +
х
о
-~ -~
о
о
При
м
е р
4.
Найти
функцию
распределения
случайной
величины
Х,
плотность
вероятности
которой
определена
формулой
1
р(х)
=
(-ОО<Х<+ОО).'
1t(l
+х
2
)
Реш
е
н
и
е
о.
Применяя
формулу
(2.3.2),
получаем
108

J
X dt 1 I
х
1
F(x)=
2
=-arctgt
=-[arctgx-arctg(-oo)]=
__
7t{l+t)
1t
-_
1t
1 1
=-+-
arctg
х.
2 1t
3
а
м
е
ч
а
н и
е
.
Полученная
функция
F(x)
удовлетворяет
условиям
(2.2.7):
11т
-+-arctg
х
=-+-
lim arctg
х=-+_·
-~
=---=0,
.
(1
1 ) 1 1 . 1 1 [
х)
1 1
х-+
- - 2 1t 2 1t
х-+
- - 2 1t 2 2 2
lim
-+-arctgx
=-+-
11т
arctgx=-+_·
-
=-+-=1.
.
(1
1 ) 1 1 . 1 1
(х)
1 1
х-+
+ - 2 1t 2 1t
х+"
- 2 1t 2 2 2
При
м
е
р
5.
Дана
функция
ЛхУ=
{О
се-ах
при
х
:5
О,
nрих>О
(0.>0).
При
каком
значении
постоянной
с
функция
j(x)
является
плотностью
распределения
вероятностей
некоторой
случайной
величины
х?
Реш
е
н
и
е.
Прежде
всего,
должно
быть
с
~
О
.
для
определения
зна
чения
с
воспользуемся
условием
(2.3.6):
J
f(x)dx=l,
cJe-
ах
dx=l'
-
:е-
ах
/+
о
-
=1,
:
=l,c=a,.
--
о
Следовательно,
плотность
распределения
имеет
вид
р(х)
=
{О
а,е-
ах
при
х
:5
О,
при
х
>
О;
о.
>
О.
При
м
е
р
6.
Найти
функцию
распределения
F(x)
случайной
вели
чины
Х,
плотность
вероятности
которой
определена
функцией
р(х)
=
f~
12-x
при
х
:5
О
их>
2,
npиО<х:51,
при
1 <
х:5
2.
Ре
w
е н
и
е.
Чтобы
найти
функцию
распределения
F(x)
,
воспользу
емся
формулой
(2.3.2).
109
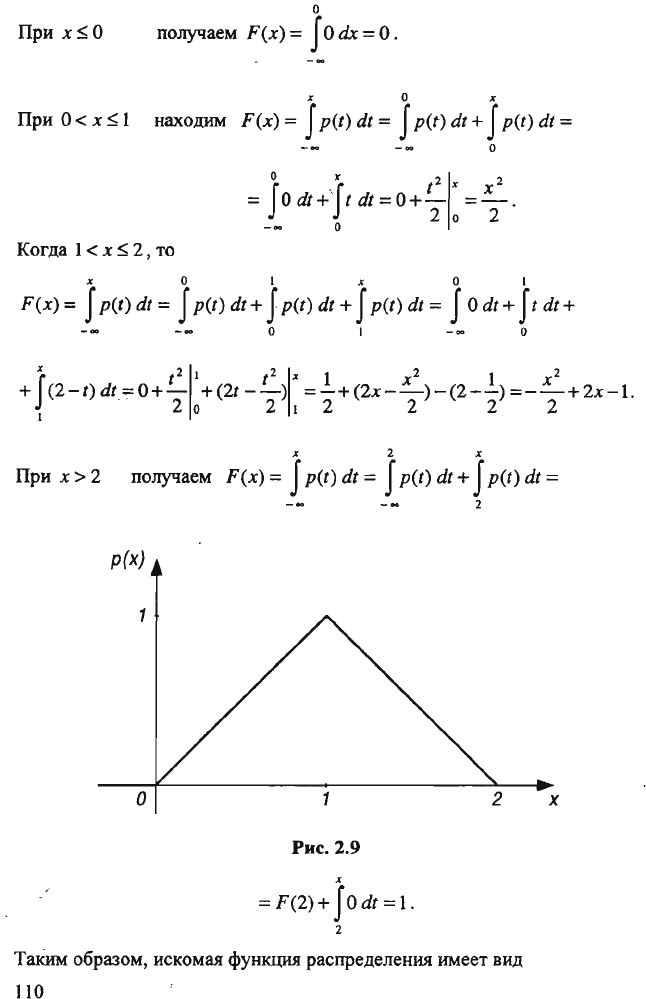
При
x:S;O
о
получаем
F{x)
=
J0dx=O.
х
О
х
При
0<
х::>
1
находим
F(x)
= J
p{t)
dt
= J
p{t)
dt
+ J
p(t)
dt
=
о
Когда
1 <
х
:s;
2,
то
х О
1
х
О
1
F(x)
= J
p(t)
dt
= J
p(t)
dt
+ J
p(t)
dt
+ J
p(t)
dt
= J
о
dt
+ J t
dt
+
о
1
О
J
X
t211
(21х
1
х
2
1
х
2
+
(2-t)
dt
=0+-
+(2t
--)
=-+(2х--)-(2--)
=--+2x-l.
··2
22
2
22
1
О
1
х
2
х
При
х>
2
получаем
F{x)
= J
p(t)
dt
= J
p(t)
dt
+ J
p(t)
dt
=
р(х)
о
Рис.
2.9
=
F(2)
+ J
о
dt
= 1.
2
ТаКим
образом,
искомая
функция
распределения
имеет
вид
110
х
