Гусак А.А., Бричикова Е.А. Теория вероятностей. Справочное пособие к решению задач
Подождите немного. Документ загружается.


величины
можно
записать
в
виде
следующей
таблицы.
Таблица
2.3
р
I
2
3
n
х
р
pq
n-l
Pq
3
а
м
е
ч а
н и
е
.
Условие
(2.1.4)
в
данном
случае
выполнено.
Действитель-
~
"'"'
,,-)
но,
принимая
во
внимание
условие
сходимости
геометрического
ряда
~
Gq
IJ=I
(
Iql
< 1 )
и
формулу
S =
_а_
для
его
суммы,
получаем
l-q
.
Задачи
1.
Задает
ли
закон
распределения
дискретной
случайной
величины
каждая
из
следующих
таблиц:
,")
х
о
1 2 3
I
4
р
0,05 0,15 0,20 0,25 0,35
б)
Х
5 6
7
8
9
р
0,1
0,2 0,3 0,4
0,15
В}
Х
S
S2
s3
I
1/2
k
Р
2/3
2/з2
2/33
2/з
k
г}
Х
i
·2
J
1/4
k
Р
1/3
115
1/2k-l
д}
Х
1/3
1/32
1/з
k
Р
·2
J
1/4
k
91

2.
Дискретная
случайная
величина
Х
имеет
закон
распределения:
х
о
0,2 0,4 0,6
0,8
Р
0,15 0,2
0,3
0,15
Чему
равна
вероятность
Р4
=
Р(Х
=
0,6)?
Постройте
многоуголь
ник
распределения.
3.
Дискретная
случайная
величина
Х
имеет
закон
распределения:
х
2 3
4
5
Р
0,15 0,30 0,25
Ps
Найдите
вероятность
РI
=
Р(Х
=
1)
и
Ps
=
Р(Х
=
5)
,
если
известно,
что
Ps
в
2
раза
больше
PI'
4.
Подбрасываются
две
симметричные
монеты,
ПОДС'lитывается
число
цифр
на
обеих
верхних
сторонах
монет.
Запишите
закон
распре
деления
случайной
величины
Х
-
число
выпадения
цифры
на
обеих
мо
нетах.
5.
В
урне
7
шаров,
из
которых
4
голубых,
а
остальные
красные.
Из
этой
урны
извлекаются
3
шара.
Найдите
закон
распределения
дискрет
ной
случайной
величины
Х
-
'Iисло
голубых
шаров
в
выборке.
6.
В
партии
из
1
О
деталей
имеется
8
стандартных.
Из
этой
партии
наудачу
взято
2
детали.
Найдите
закон
распределения
дискретной
слу
чайной
величины,
равной
числу
стандартных
деталей
в
выборке.
7.
Подбрасывается
три
игральных
кубика,
подсчитывается
число
оч
ков на
верхних
гранях
кубиков.
Найдите
закон
распределения
дискретной
случайной
величины,
равной
сумме
очков,
выпавших
на трех
кубиках.
Ответы
1.
а)
да;
б)
нет;
в)
да;
г)
нет;
д)
нет.
2.
Р4
=
0,2.
З.
РI
==
0,10,
Рз
==
0,20;
7.
У
к а
з
а
н
и
е.
Всего
равновозможных
элементарных
исходов
63
==
216.
Число
исходов,
благоприятствующих
суммам:
3
и
18
-
1;
4
и
17
- 3; 5
и
16
- 6; 6
и
15-10;
7и
14-15;
8
и
13
-21;
9и
12-25;
10и
11-27.
Вопросы
1.
Что
называют
случайной
величиной?
2.
Какую
величину
называют
дискретной
случайной
величиной?
3.
Какую
величину
называют
непрерывной
случайной
величиной?
4.
Что
называют
законом
распределения
дискретной
случайной
ве
личины?
5.
Как
задают
закон
распределения
дискретной
случайной
величины,
92

принимаю
щей
конечное
множество
значений?
6.
Что
называют
многоугольником
распределения?
7.
Как
задают
закон
распределения
дискретной
случайной
величины,
принимающей
счетное
множество
значений?
§ 2.2.
Функция
распределения
Функцией
расnределения
l
случайной
величины
Х
называется
функ
ция
действительной
переменной
х,
определяемая
равенством
F(x)
=
Р(Х
<
х),
(2.2.])
где
Р(Х
<
х)
-
вероятность
того,
что
случайная
величина
Х
примет
зна
чение,
меньшее
х.
Геометрически
это
означает
следующее:
F(x) -
веро
ятность
того,
что
случайная
величина
Х
примет
значение,
которое
изо
бражается
точкой
на
числовой
прямой,
расположенной
слева
от
точки
х
(рис.
2.2).
Случайная
вели
чина
называется
не
прерывной,
если
ее
функция
распределе
ния
F(x)
=
Р(Х
<
х)
о
•
является
непрерывно
дифференцируемой.
х
•
х
Рис.
2.2
Вероятность
того,
что
случайная
величина
Х
примет
значение
из
по
луинтервала
[а,
~),
равна
разности
значений
ее
функции
р-аспределения
F(x)
на
концах
этого
полуинтервала:
Р(а
$.
Х
<
~)
=
Fф)
-
F(a)
.
(2.2.2)
Функция
распределения
F(x)
случайной
величины
Х
имеет
следую
щие
свойства.
].
Все
значения
функции
распределения
F(x)
принадлежат
отрезку
[О,
1],
т.е.
О$.
F(x)
$.1
. (2.2.3)
Это
следует
из
определения
(2.2.1)
и
свойств
вероятности.
2.
Функция
распределения
F(x)
является
неубывающей,
т.е.
если
х\
<
х
2
,
то
(2.2.4)
\
Функцию
распределения
называют
также
интегрЩ/ьной
функцией,
или
uнтегрЩ/ьным
законом
распределения
случайной
величины
Х.
93

З.
Функция
F(x)
в
точке
ХО
непрерывна
слева,
Т.е.
(2.2.5)
4.
Если
все
возможные
значения
случайной
величины
Х
принадле
жат
интервалу
(а, Ь),
то
для
ее
функции
распределения
F(x)
F(x)
=
о
при
х::;;
а,
F(x)
= 1
при
х"?
Ь
.
(2.2.6)
5.
Если
все
возможные
значения
случайной
величины
Х
принадле
жат
бесконечному
интервалу
(
-00,
+
00
),
то
lim
F(x)
=
О,
lim
F(x)
= 1.
(2.2.7)
х-+
_оа
X~
+00
На
основании
свойств
функции
распределения
F(x)
можно
судить
об
особенностях
ее
графика
(рис.
2.3
а,
6).
а
о
х
6
х
Рис.
2.3
Если
Х
-
непрерывная
случайная
величина,
то
вероятность
того,
что
она
примет
одно,
заданное
определенное
значение,
равна
нулю:
Р(Х
=а)
=0,
(2.2.8)
поэтому
выполняются
равенства:
Р(а::;;
Х
::;;~)
=
Р(а
<
Х
::;;~)
=
Р(а::;;
Х
<~)
=
Р(а
<
Х
<~),
(2.2.9)
94
Р(а
<
Х
<
Р)
=
F(P)
-
F(a)
.
(2.2.1
О)
Функция
распределения
F(x)
для
дискретной
случайной
величины
Х,
которая
может
принимать
значения
XI,
Х2,
.•.
Х
n
С
соответствующими
вероятностями,
имеет
вид
F(x)
=
LP(X
= x
k
),
(2.2.1] )
ХА·<Х
где
символ
X
k
<
Х
означает,
что
суммируются
вероятности
тех
значе
ний,
которые
меньше
Х.
Функция
(2.2.1 ])
является
разрывной.
При
м
е р
1.
Дана
функция
F(x)=
7t
О,
если
х
<
__
О
-
2'
7t
cos
х,
если
- - <
х
::;
О;
2
1,
если
х
>
о.
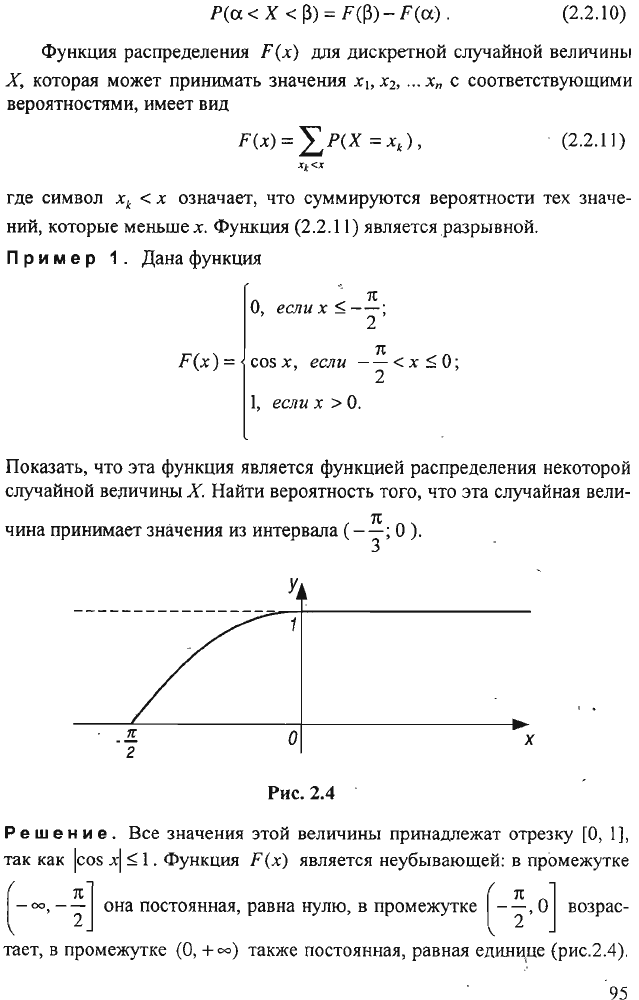
Показать,
что
эта
функция
является
функцией
распределения
некоторой
случайной
ве;пичиныI
Х.
Найти
вероятность
того,
что
эта
случайная
вели-
7t
чина
принимает
значения
из
интервала
(--;
О).
3
у
----------------~---+-------------------
1r
2
о
Рис.
2.4
х
Реш
е н и
е.
Все
значения
этой величиныI
принадлежат
отрезку
[О,
1],
так
как
Icos
xl::;
1.
Функция
F(x)
является
неубывающей:
в
промежутке
( -
00,
-
~]
она
постоянная,
равна
нулю,
в
промежутке
(-
~,
о]
возрас
тает,
в
промежутке
(О,
+
00)
также
постоянная,
равная
едини,це
(рис.2.4).
95
Функция
непрерывна
в
каждой
точке
хо
области
ее
определения
-
про
межутка
(
-00,
+
00
),
поэтому
непрерывна
слева и
справа,
Т.е.
выполняет-
ся
равенство
(2.2.5).
Выполняются
и
равенства
(2.2.7).
Следовательно,
функция
F(x)
удовлетворяет
всем
свойствам,
ха-
рактерным
для
функции
распределения.
Функция
F(x)
является
функ
цией
распределения
некоторой
случайной
величины
Х.
Все
значения
случайной
величины
Х
при
надлежат
интервалу
n n
(--;
О),
поэтому
выполняются
и
равенства
(2.2.6)
при
а
=
--
и Ь
=
О.
2 2
В
соответствии
с
формулой
(2.2.1
О)
находим
искомую
вероятность
n n I 1
Р(--<
Х
<
О)
=
F(O)-
F(--)
=
1--
=-.
3 3 2 2
п
р
им
е
р
2.
Дана
функция
1
0,
если
х
::;
О;
F(x)=
х
2
,
еслиО<х
::;2;
1,
если
х
>
2.
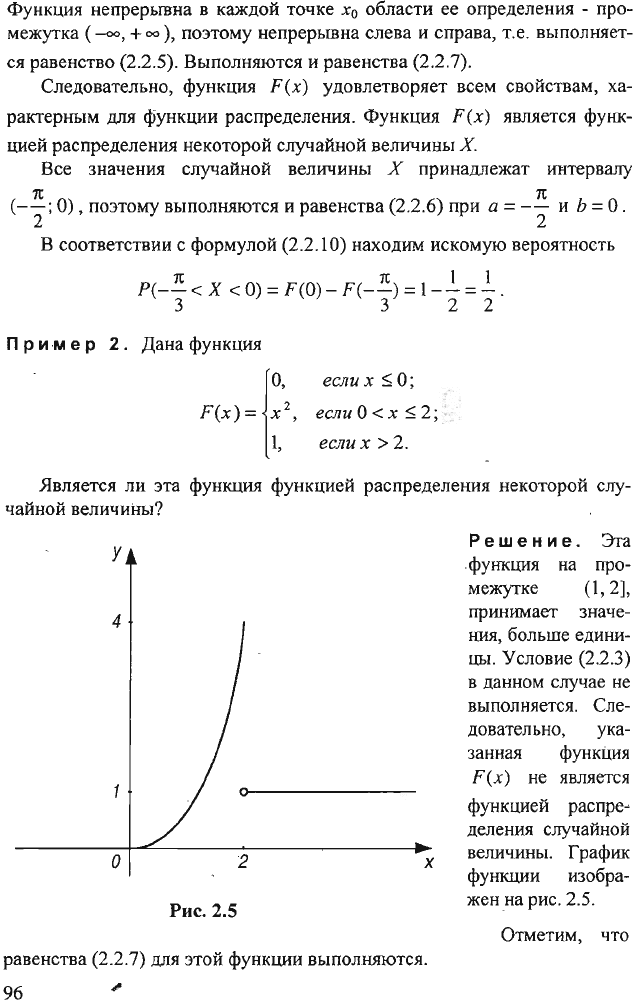
Является
ли
эта
функция
функцией
распределения
некоторой
слу
чайной
величины?
у
4
о
х
Рис.
2.5
равенства
(2.2.7)
для
этой
функции
выполняются.
96
Решение.
эта
функция
на про
межутке
(1,2],
принимает
значе
ния,
больше
едини
цы.
Условие
(2.2.3)
в
данном
случае
не
выполняется.
Сле
довательно,
ука
занная
функция
F(x)
не
является
функцией
распре"
деления
случайной
величины.
График
функции
изобра
жен
на
рис.
2.5.
Отметим,
что

При
м
е
р
З.
Является
ли
функцией
распределения
случайной
вели
чины
функция
1
F(x)
=--2
(-оо<х<+оо)?
l+х
р
е
w
е
н и
е.
Данная
функция
не
является
функцией
распределения
случайной
величины,
так как
в
про
межутке
(О,
+
00)
она
убьmает;
нера-
венство
(2.2.4)
в
,этом
промежутке
не
выполняется.
График
функции
изо-
О х
бражен
на
рис.
2.6.
Отметим,
что
все
значения
дан-.
Рис.
2.6
ной
функции
принадлежат
промежут-
ку
(О,
1],
Т.е.
функция
удовлетворяет
неравенствам
(2.2.3).
Удовлетворя
ет
она и
первому
из
равенств
(2.2.7);
второе
из
этих
равенств
для
данной
функции
не
выполняется.
При
м
е
р
4.
Случайные
величины
Х
1
и
Х
2
имеют
функции
распреде
ления
F
1
(х)
И
F
2
(х)
соответственно.
Доказать,
что
функция
F(x)
=
С
1
F
1
(х)
+
С
2
F
2
(х)
является
функцией
распределения
некоторой
случайной
величины
)С,
здесь
С
1
и
С
2
-
неотрицательные
числа,
сумма
которых
равна
единице.
Реш
е н
и
е.
ПоскольКу
F
1
(х)
И
F
2
(х)
-
функции
распределения,
то
для
них
выполняются
условия
(2.2.3) - (2.2.5), (2.2.7).
Принимая
во
внимание
эти
условия,
получаем:
0~F(X)=CIFI(X)+C2F2(X)~CI+C2
=1;
O~F(x)~I;
F(x
l
);=
C1F
1
(x
l
)
+ C
2
F
2
(x
l
)
~
C,F
,
(х
2
)
+
C2F~
(х
2
)
=
F(x
2
),
F(x
,
)
~
F(x
2
);
F(x
o
-О)
=
C,F,(x
o
-0)+С
2
F
2
(х
О
-О)
= CIFI(XO)+C2F2(XO) =
р(х
о
),
F(x
o
-О)
=
F(x
o
);
lim
F(x)
= lim
(C
,F,
(x)+CzF2(X»
=
С
1
• lim
~(X)+C2
. lim F
2
(x)
=
х-+_
х-...+-оо
x-t--
x-t-oo
lim
F(x)=O;
X~--
43ак.
1874.. 97

liт
F(x)=
liт
(C,F,(x)+C
2
F
2
(x»=C,·
liт
F,(x)+C
2
·
lim F
2
(x)=
х-++оо
х-++оо
х-++оо
х-++оо
lim
F(x)
=
1.
х--+
+00
Таким
образом,
условиям
(2.2.3) - (2.2.5), (2.2.7)
удовлетворяет
и
фунхция
F(x).
Значит,
функция
F(x)=C,F,(x)+C
2
F
2
(x),
где
С,
+
с
2 = 1,
является
функцией
распределения
некоторой
случайной
ве
личиных.
При
м
е
р
5.
Закон
распределения
дискретной
случайной
величин!?!
задан
следующей
таблицей:
х
О
2 3
Р
0,2 0,4 0,3
0,1
Найти
фунхцию
распределения
этой
случайной
величины.
Реш
е
н и
е.
для
построения
функции
распределения
F(x)
дискрет
ной
случайной
величины
Х
пользуемся
формулой
(2.2.11).
1.
При
х
~
О
F(x)
= L
Р(Х
= x
k
)
=
О
.
Xk<O
2.
При
x<O~l
F(x)
=
LP(X=xk)=P(X=0)=0,2.
x.t<1
3.
При
1 <
х
~
2
F(x)
=
LP(X
= x
k
)
=
Р(Х
=
О)
+
Р(Х
=
1)
=
xk<2
= 0,2 + 0,4 = 0,6.
4.
При
2 <
х
~
3
F(x)
= L
Р(Х
= x
k
)
=
Р(Х
=
О)
+
Р(Х
=
1)
+
Р(Х
= 2) =
5.
При
х>3
X..I::<3
=0,2+0,4+0,3=
0,9.
F(x)
=р(х
=О)+Р(Х
= 1)+
Р(Х
=
2)+
Р(Х
=
3)
=
=
0,2+0,4+0,3+0,1
=
1.
График
функции
F(x)
изображен
на
рис.
2.7.
98

При
м
е
р
6.
В
партии
из
1
О
деталей
име
.
ется
8
стандартных.
Из
этой
пар
тии
наудачу
взято
2
детали.
Найти
функцию
распределения
дискретной
случайной
величины,
рав
ной
числу
стандартных
деталей
в
выборке.
Реш
е н и
е.
Найдем
сначала
закон
распределе
ния
данной
случайной
ве-
у
0,9
0,6
0---
о---
о---
0,2С)---
о
2 3
Рис.
2.7
х
личины
Х.
эта
величина
может
принимать
три
XI=O,
Х2=
1,
хз=2.
Вычислим
вероятности
этих
значений:
значения:
-
с
О
·с
2
1
C~·C~
16
PI=P(X=O)=
822
=-'Р2=Р(Х=I)=--2-=-'
C
IO
45 C
IO
45
с
2
•
СО
28
Рз
=
Р(Х
= 2) = 8 2 2 =
C
IO
45
Следовательно,
закон
распределения
данной
случайной
величины
можно
задать
таблицей
Х
О
Р
45
16
45
2
28
45
в
соответствии
с
формулой
(2.2.11)
строим
функцию
распределения.
1.
При
х::;О
F(x)
=
LP(X
=xk)=O.
xt<O
2.
При
О
<Х::;
1
F(x)=
""
Р(Х
=xk)=P(X
=0)=_1
.
L.J
45
Xk<l
3.
При
1 <
Х::;
2
F(x)
=
LP(X
=xk)=P(X
=О)+Р(Х
=1)=
Xt<2
1 .16
17
=-+-=-.
45 45 45
4.
При
Х
> 2
1
16
28
F(x)=P(X
=О)+Р(Х
=1)+Р(Х
=2)=-+-+--:-=1.
.
45
45 45
99

При
м
е
р
7.
Случайная
величина
Х
задана
функцией
распределения
1
0
nрих
:::;0,
F(x)=
х/2
nриО<х
:::;2,
1
nрих
> 2.
Найти
вероятность
того,
что
в
результате
испытания
случайная
величина
Х
примет
значение,
заключенное
в
интервале
(1, 2).
Решение.
Для
этого
интервала
F(x)=x/2.
В
соответствии
с
фор
мулой
(2.2.2)
получаем:
Р(1
<
Х
< 2) =
F(2)-F(1)
=
(2/2)-(1/2)
= 0,5.
При
м
е
р
8.
Случайная
величина
Х
задана
функцией
распределения
1
0
nрих:::;
О,
F(x)=
х/3
nриО<х
:::;3,
1
при
х
> 3.
Найти
вероятность
того,
что
в
результате
испытания
величина
Х
примет
значение
из
интервала
(2, 3).
Реш
е
н
и
е.
По
формуле
(2.2.2)
находим:
Р(2
<
х
:::;
3) =
F(3)-
F(2)
=
(3/3)-(2/3)
=
1-2/3_;
1/3.
При
м
е
р
9.
Случайная
величина
Х
задана
функцией
распределения
1
0
при
х
:::;0,
F(x)
= sin
х
при
О
<
х:::;
1t/2,
1
при
х
> 1t12.
Найти
вероятность
того,
что
в
результате
испытания
величина
Х
примет
значение
из
интервала
(4,5).
Решение.
Так
как
P(4<X<5)=F(5)-F(4)=1-1=0,
то
данная
величинаХ
таких
значений
не
принимает.
3
а
м
е
ч а
н
и
е.
Этот
результат
можно
получить
и
с
помощью
соотноше
ний
(2.2_6)_
Все
значения
этой
величины
принадлежат
промежутку
(О,
?/2).
При
м
е р
1
О.
Два
стрелка
делают
по
одному
выстрелу
в
одну
ми
шень.
Вероятность
попадания
для
первого
стрелка
при
одном
выстреле
РI
=
0,5,
для
второго
-
Р2
= 0,4 .
Дискретная
случайная
величина
Х
-
число
попаданий
в
мишень.
Найти
функцию
распределению
этой
слу
чайной
величины.
Найти
вероятность
события
Х
;::
] .
100
