Гусак А.А., Бричикова Е.А. Теория вероятностей. Справочное пособие к решению задач
Подождите немного. Документ загружается.

F(x)
о
Рис.
2.10
nрих
~O,
при
О
<
х
~
1,
при
1
<х
~2,
nрих
>
2.
2
х
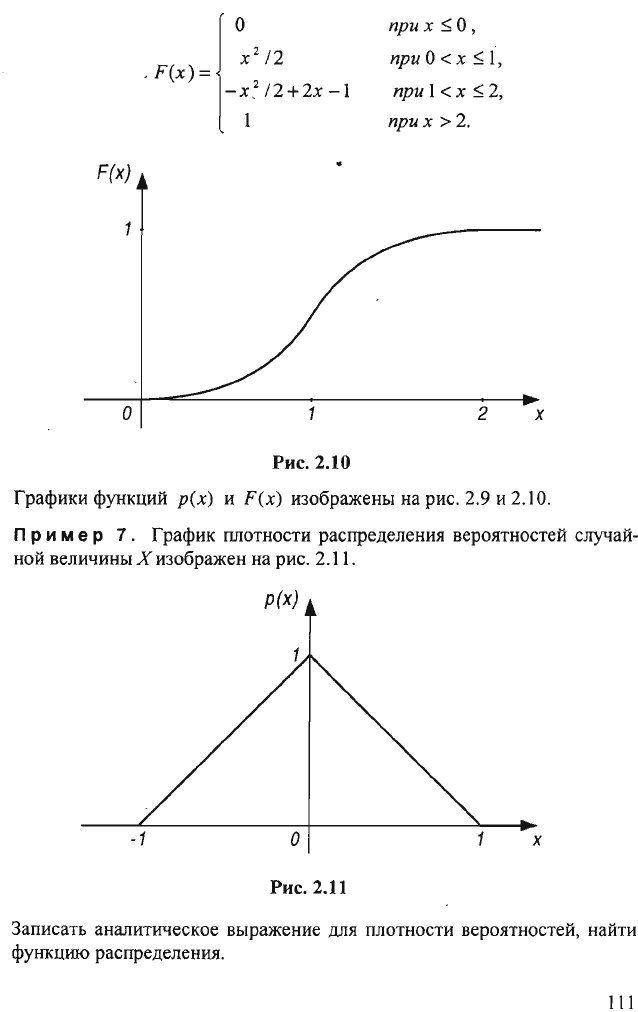
Графики
функций
р(х)
и
F(x)
изображены
на
рис.
2.9
и
2.10.
При
м
е р
7.
График
ШIотности
распределения
вероятностей
случай
ной
величины
Х
изображен
на
рис.
2.1
1.
р(х)
-1
о
х
Рис.
2.11
Записать
аналитическое
выражение
для
плотности
вероятностей,
найти
функцию
распределения.
111

Реш
е
н и
е.
Пользуясь
графиком,
записываем
аналитическое
выражение
ШIотности
распределения
вероЯ'rНОстей
данной
случайной
величины:
р(х)
=
{~+
1
-х+l
при
Ixl>
1,
- ,
при
-1
<
х
::;0,
при
0<
х
::;1.
в
соответствии
с
формулой
(2.3.2)
находим
функцию
распределения:
при
х::;-l
получаем
J
о
dx =
О
;
при-1
<
х::;о
х
-1
х
(t+1)2I
X
(х+1)2
F(x)
= f
p(t)dt=
f
Odt
+f(t+l)dt=O+--
=--;
2 -1 2
-~
-~-I
х
-1
О х
F(x)
= f
p(t)dt=
fOdx+
f(X+l)dx+
f(-t+1)dt=
-1
о
=(Х+1)21°
_O_t)2I
Х
=.l+.l_O-Х)2
=1_(1-Х/
2 2 2 2 2 2
-1
О
при
х>
1
х
-1
О
I
х
F(x)
= f
p(t)dt=
fOdx+
f(X+l)dx+
f(-X+l)dx+fodx=
-1
о
1
Следовательно,
функция
распределения
имеет
вид:
F(x)
=
112
о
(х+1)2
2
1-
(l-х)2
2
при
-1
<
х::;О,
при
х>
1.
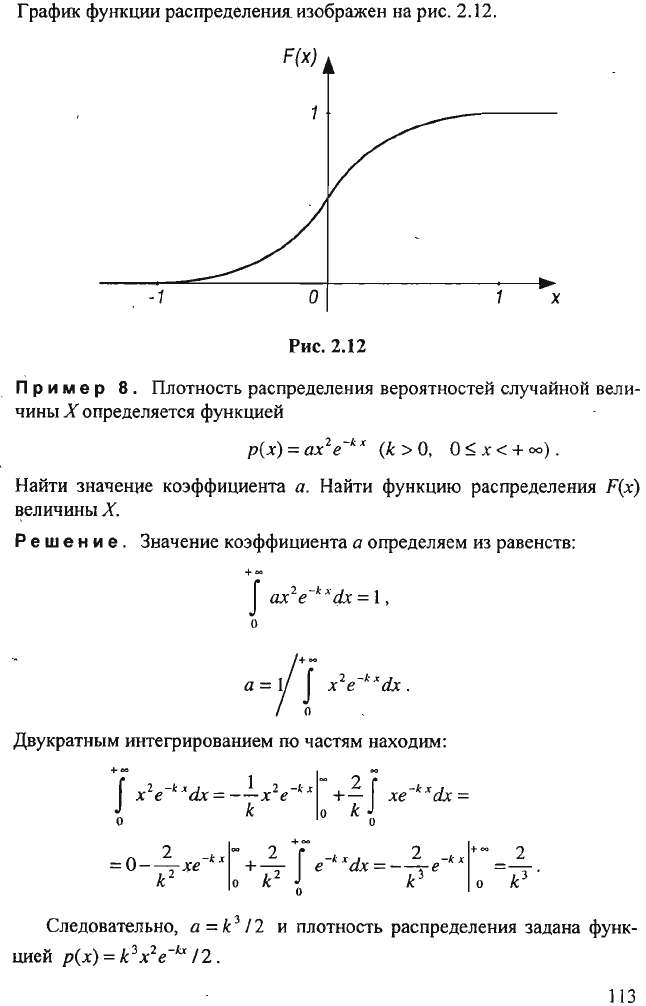
График
функции
распределения.
изображен
на
рис.
2.12.
F(x)
-1
х
Рис.
2.12
При
м
е р
8.
Плотность
распределеяия
вероятностей
случайной
вели
чины
Х
определяется
функцией
р(х)
= ax
2
e-
kx
(k
>
О,
О$;
х
< +
00).
Найти
значеIЩе
коэффициента
а.
Найти
функцию
распределения
F(x)
величиных.
Реш
е
н и
е.
Значение
коэффициента
а
определяем
из
равенств:
+~
f ax
2
e-
kx
dx=l,
о
Двукратным
интегрированием
по
частям
находим:
J
x2e-kХdx=_fх2е-kХI:
+f
j xe-kxdx=
о
о
+-
I
2
-k
х
- 2
-k
Х
2
-k
х
+ - 2
=O-J;2xe I
+J;2
f
е
dX=-/Jе
=k3'
о о о
Следовательно,
а
= k
з
/2
и
плотность
распределения
задана
функ
цией
р(х)
=
е
х
2
е-
и
/2.
113

Функция
распределения
F(x)
имеет
вид
< 3 2 2
F()
f
k 2
-k'd
1 k
х
+ 2 kx + 2
-k
<
Х
=
-t
е
t=
-
е
.
о
2 2
При
м
е
р
9.
Задана
функция
f(x)
=
ае
-lxJ
.
При
каком
значении
а
ее
можно
рассматривать
как
плотность
распределения
вероятностей
неко
торойслучайнойвеличиныА7
Реш
е
н и
е.
Если
f(x)
-
плотность
вероятности,
то
должно
выпол
няться
условие
(2.3.6).
Следовательно,
Tae-'<'dx=a
J
eXdx+aT
e-xdx=aexl_o~
-ae-xl+o~
=
=а(1-0)-а(0-1)=2а=1,
т.е.
a=1I2.
Итак,
функция
р(х)
=.!..е
-1<1
является
плотностью
распределения
ве-
2
роятностей
некоторой случайной
величины.
При
м
е р
1
о.
Случайная
величина
Х
задана
функцией
распределения
{
О
при
x~O,
F(x)
=
l(l-C
2
0SX)
о
<
при
< х
_п,
при
х
>
п.
Найти
плотность
распределения
величины
Х.
Вычислить
вероятность
того,
что
случайная
величина
Х
примет
значения
из
интервала
(п/3,
п/2).
Реш
е н и
е.
Плотность
вероятности
рех)
и
функция
распределения
F(x)
случайной
величины
Х
связаны
соотношением
(2.3.5),
т.е.
F'(x)
=
р(х).
Следовательно,
р(х)=О
при
х
=0
и
х>п,
p(x)=((l-cosx)12)
=
(sin
х)/2
в
интервале
(О,
п)
.
По
формуле
(2.3.3)
находим
·искомую
вероятность
114

При
м
е
р
1
1.
Случайная
величина
Х
имеет
мотность
распределения
с
р(х)
= r
-х·
е
+е
Найти
значение
параметра
с,
функцию
распределения
F(x).
Ре
w
е н и
е.
В
соответствИJi
с
условием
(2.3 .6)
должно
быть
Вычислим
этот
несобственный
интеграл:
+00
+_
О
+00
f
с
dx
=cf
~ш
=
cf
d(e
r
)
+cf
d(e
r
)
=
е
К
+е--
Х
l+е
2К
1+(е
К
)2
_1+(е
Х
)2
--
о
1
0
1+-
n
=
с
arctg
е
К
+
с
arctg
е
Х
=
с
. - .
-
-_
о
2
n - 2
Следовательно,
С·
- =
1,
с
=
-;
мотность
вероятности
определяет-
2 n
ся
функцией
2
р(х)=
(К
-Х)
n
е
+е
По
формуле
(2.3.2)
находим
функцшо
распределения
данной
слу
чайной
величины
Х:
F(x)
=
fX
2
dt
=
~
fX
di
~
~
arctg e'l r =
~arctg
е
Х
,
ще'+е-l)
n
__
e'+e-l
1t
-_
1t
F(x)
=
~arctg
е
Х
•
1t
При
м
е
р
1
2.
Случайная
величина
Х
задана
функцией
распределения
о
-
(а+х)2
2
а
2
F(x)
=
1-
(а-х)2
2
а
2
при
х
S;
-а,
при
-
а
<
х
S;
О,
при
0<
х
S;
а,
прих
>
а
..
115

Найти
плотность
распределения
случайной
величины
Х.
Реш
е н и
е.
Пользуясь
равенством
(2.3.5),
находим
функцию
р(х)
.
Так
как
то
плотность
распределения
случайной
величины
Х
имеет
вид
о
nрих
~
-а,
nри-а<х
~O,
р(х)=
nриО<х
~
а,
о
nрих
>
а.
Задачи
1.
Является
ли
плотностью
распределения
некоторой случайной
ве
личины
каждая
из
следующих
функций:
116
{
О
при
х
~
О
их>
1 ,
а)
лх)
=
1
npиO<x~l;
{
О
при
х
~
О
их>
1 ,
б)
ЛХ)=
x{l-x)
npиO<x~l;
{
О
npиx~-1иx>1,
в)
ЛХ)
=
зх2/2
при
-1
<
х
~
1 ;
х
г)
ЛХ)=--2
(-оо<х<+оо)?
-1+х
2.
Функция
распределения
случайной
величины
Х
задана
формулами
1
0
при
х
~
О,
F(x)
=
сх
3
при
О
<
х
~
1 ,
1 -
nрих
> 1.

Найдите
значение
коэффициента
с
и
плотность
распределения
веро
ятностей
случайной
величины
Х.
3.
Функция
распределения
случайной
величины
Х
имеет
вид
1
0
nрих
:5:0,
F(x)=
х
2
nриО<х
:5:1,
1
npux>l.
Найдите
плотность
распределения
случайной
величины
Х.
Чему
равна
вероятность
того,
что
случайная
величина
Х
примет
значение
из
интервала
(0,5; 1)? -
4.
Плотность
распределения
случайной
величины
Х
задана
функцией
nрих:5:
О,
nрих
>
О.
Найдите
вероятность
того,
что
значение
случайной
величины
Х
при
надлежит
интервалу
(2, 3).
5.
Функция
распределения
случайной
величины
Х
имеет
вид
1
0
1/2
F(x)=
~X+1)/2
nрих:5:
-1,
nри-I
<
х:5:
О,
nриО
<
х:5:
1,
nрих
>
1.
Найдите
плотность
распределения
р(х)
этой
"случайной
величины.
Чему
равна
вероятность
того,
что
значение
случайной
величины
Х
при
надлежит
интервалу
(0,5; I)?
б.График
плотности
распределения
вероятно
стей
случайной
величины
Х
имеет
вид,
изображен
ный
на
рис.
2.l3.
Запишите
аналитиче
ское
выражение
для
плот
ности
распределения
р(х).
Найдите
функцию
распределения
случайной
величиных.
-а
а
х
Рис.
2.13
117

Ответы
1.
а)
да;
б)
нет;
в)
да;
г)
нет
(Лх)
<
о
при
х
<
О)
. 2.
c=l;
nрих
~
О,
р(х
) =
3х
2
при
О
<
х
~
1,
1
0
nрих
~O,
при
О<Х
~
1,
Р(0,5
<Х
<
1)=
0,75.
при
х
>
1;
о
nрих
> 1.
4.0,2.5.
Р
= 0,5.6.
У
к а
3
а
н
и
е.
См.
пример7.
Вопросы
1.,
Что
называют
плотностью
распределения
случайной
величины?
2.
Как
по-другому
называют
плотность
распределения?
3.
Что
называют
кривой
распределения?
4.
Как
с
помощью
плотности
распределения
найти
вероятность
по
падания
значений
случайной
величины
Х
в
интервал
(а,
f3)?
5.
Какие
свойства
имеет
плотность
распределения?
6.
Как
выражается
функция
распределения
через
плотность
распре
деления?
7.
Как
выражается
плотность
распределения
через
функцию
распре
деления?
§ 2.4.
Математическое
ожидание
случайной
величины
Мате.матическим
ожиданием
дискретной
случайной
величины
Х,
принимающей
конечное
множество
значений
с
законом
распределения
Р(Х
= X
k
)
=
Pk
, k =
1,
2, ... ,
n,
(2.4.1 )
(2.4.2)
называется
сумма
произведений
ее
значений
на
их
соответствующие
вероятности:
"
М(Х)
=Х,Р,
+Х
2
Р2
+
...
+Х"Р",
М(Х)
=
LXkPk'
(2.4.3)
k='
Для
обозначения
математического
ожидания
используются
и
другие
символы:
ЕХ,
а,
тх.
Математическое
ожидание
дискретной
случайной
величины
при
ближенно
равно
среднему
арифметическому
всех
ее
возможных
значе
ний.
Вследствие
этого
математическое
ожидание
случайной
величины
называют
ее
средним
значением.
118

3
а
м
е
ч
а
н
и
е.
Математическое
ожидание
сЛучайной
величины
называют
также
центром
распределения.
Это
название
заимствовано
из
механики
и
объ
ясняется
следующим:
если
в
точках
X
1
,
Х
2
,
...
,
Х"
оси
ОХ
находятся
соответст-
венно
массы
PI'
Р2,
... ,
Р"
,
то
координата
Х
иентра
тяжести
системы
материаль
ных
точек
вычисляется
по
формуле
Поскольку
выполняется
условие
(2.4.2),
то
Х=
!.XkPk
=М(Х).
k=1
Математическое
ожидание
дискретной
случайной
величины,
при
нимающей
бесконечную
последовательность
значений
с
законом
рас
пределения
P(X=Xk)=Pk'
k=J,2,З,
... ,
(2.4.4)
(2.4.5)
определяется
формулой
М(Х)
=
~>kPk'
(2:4.6)
k=1
если
этот
ряд
сходится
абсолютно.
Математическое
ожидание
непрерывной
случайной
величины
Х,
все
значения
которой
принадлежат
отрезку
[«,13],
а Р(Х)
-
ее
плотность
вероятностей,
определяется
формулой
~
М(Х)
= f
ХР(Х)
dx
. (2.4.7)
а
Если
все
значения
непрерывной
случайной
величины
Х
принадлежат
бесконечному
промежутку
(-
00,
+
00),
а Р(Х)
-
ее
плотность
вероятно-
стей,
то
математическое
ожидание
определяется
формулой
+~
М(Х)
-=
f
ХР(Х)
ш,
(2.4.8)
когда
этот
несобственный
интеграл
сходится
абсолютно.
119

Отметим,
что
математическое
ожидание
случайной
величины
есть
величина
постоянная.
Свойства
математического
ожидания
случайной
величины.
.
1.
Значение
математического
ожидания
случайной
величины
Х
за
КJПOчено
между
ее
наименьшим
и
наибольшим
значениями:
а
'5:.
М(Х)
'5:.Ь,
(2.4.9)
где
а
-
наименьшее,
Ь
-
наибольшее
значение
величины
Х.
2.
Математическое
ожидание
постоянной
величиныI
равно
этой
по
стоянной:
м(е)=;:е
(е
= const). (2.4.10)
3.
Постоянный
множитель
можно
вынести
за
знак
математического
ожидания:
м(ех)=ем(х)
(е
= const). (2.4.11)
4.
Математическое
ожидание
суммы
двух
случайных
величин
равно
сумме
их
математических
ожиданий:
М(Х
+
У)
=
М(Х)
+
М(У)
.
(2.4.12)
Это
равенство
распространяется
на
n
случайных
величин:
М(Х,
+Х
2
+
...
+Х:,)
=
М(Х,)+М(Х
2
)+
...
+
М(Х,,).
(2.4.13)
5.
Математическое
ожидание
разности
двух
случайных
величин
равно
разности
их
математических
ожиданий:
М(Х
-
У)
=
М(Х)
-
М(У)
. (2.4.14)
6.
Математическое
ожидание
произведения
двух
незавuсuмblX
слу
чайных
величин
равно
произведеюno
матема1ических
ожиданий
этих
величин:-
М(Х·
У)
=
М(Х)·
М(У).
(2.4.15)
это
равенство
распространяется
на
n
независимых
случайных
величин
(2.4.16)
При
м
е р
1.
Найти
математическое
ожидание_
дискретной
случайной
величины,
закон
распределения
которой
задан
таблицей
Х
3
4
5 6 7
р
0,1
0,2
0,4
-0,2
0,1
120
