Гусак А.А., Бричикова Е.А. Теория вероятностей. Справочное пособие к решению задач
Подождите немного. Документ загружается.


изделий
от
общего
объема
их
производства,
на
второй
- 25%,
на
третьей
-
остальная
часть
продукции.
Каждая
из
линий
характеризуется
соответ
ственно
следующими
процентами
годности
линий:
97%, 98%, 96%.
Нау
гад
взятое
изделие,
выпущенное
предприятием,
оказалось
бракованным.
Определить
вероятности
того,
что
это
изделие
изготовлено
на
первой,
второй
и третьей
линиях.
Реш
е
н
и
е.
Введем
обозначения:
А
-
событие,
состоящее
в
том,
<iTO
наугад
взятое
изделие
оказалось
бракованным;
Н"
Н
2'
Н
3 -
гипотезы,
состоящие
в
том,
что
изделие
изготовлено
соответственно
на
первой,
второй
и
третьей линиях.
В
соответствии
с
условием
задачи
имеем:
Р(Н
j)
= 0,30;
Р(Н
2)
= 0,25;
Р(Н
3)
= 0,45;
Р(А
/ H
j
)
= 0,03,
Р(А/
Н
2)
=0,02,
Р(А
/
Н
З
)=
0,04.
По
формуле
полной
вероятности
получаем
Р(А)
= 0,30·0,03 + 0,25 · 0,02 + 0,45 .0,04 = 0,032 .
в
соответствии
с
формулами
Бейеса
находим
искомые
вероятности
:
Р(Н
/А)=
P(Hj)P(A/H,)
= 0,30·0,03
=0281'
,
Р(А)
0,032"
Р(Н
/
А)
=
Р(Н
2
)Р(А/
H z) = 0,25 ·0,02
=0156'
2
Р(А)
0,032"
Р(Н
/А)=
Р(Нз)Р(А/Н
з
)
= 0,45·0,04
=0563.
3
Р(А)
0,032'
При
м
е
р
8.
В
первой
урне
2
голубых
и
6
красных
шаров,
во
второй
-
4
голубых
и
2
красных.
Из
первой
урны
наудачу
переложили
2
шара
во
вторую,
после
чего
из
второй
урны
наудачу
достали
один
шар.
Какова
вероятность
того,
что
этот
шар
голубой?
Предположим,
что
шар,
взятый
из
второй
урны,
оказался
голубым
.
Какова
вероятность
того,
что
из
первой
урны
во
вторую
были
переложе
ны
2
голубых
шара?
Реш
е
н
и
е.
Введем
обозначения:
событие
А
-
"шар,
извлеченный
из
второй
урны,
голубой";
гипотезы
Н,
-
"из
первой
урны
во
вторую
пере-
ложены
два
голубых
шара",
Н 2 -
"переложены
два
разноЦветных
шара",
Н
3
~
"переложены
два
красных
шара".
8]

Вычислим
вероятности
гипотез
Н;
и
условные
вероятности
Р(АI
Н;)
(i
=
1,2,3):
Р(Н)=
с;
=_1
Р(Н)=
c~
·c~
=~
Р(Н
)=
ci
=~.
I
с'-
28
' 2
с
2
28
' 3
с
2
28
'
8 8 8
351
Р(АI
H
1
)
= --',
Р(АI
Н
2
)
=-,
Р(АI
Н
З
)
=-.
482
По
формуле
полной
вероятности
получим
ответ
на
первый
вопрос:
1 3
12
5
15
1 9
Р(А)=-·-+_·_+_·_=-.
28
4 28 8 28 2
16
Чтобы
ответить
на
второй
вопрос,
воспользуемся
формулой
Бейеса:
;(Н
IA)=
P(H1)P(AIH
1
)
=(_1
.~J:~=~.
I
Р(А)
28
4
16
21
Задачи
1.
На
предприятии,
изготовляющем
болты,
первая
машина
произво
дит
30%,
вторая
- 25%,
третья
- 45%
всех изделий.
Брак
в
их
продукции
составляет
соответственно
2%, 1 %, 3%.
Найдите
вероятности
того,
что
случайно
выбранный
болт,
произведенный
первой,
второй
и третьей
машинами,
оказался
дефектным.
2.
Партия
транзисторов,
среди
которы!'
10%
дефектных,
поступила
·на
проверку.
Схема
проверки
такова,
что
с
вероятностью
0,95
обнару
живает
дефект
(если
он
есть),
и
существует
ненулевая
вероятность
0,03
того,
что
исправный
транзистор
будет
признан
дефектным.
Случайно
выбранный
из
партии
транзистор
был
признан
дефектным.
Какова
веро
ятность
того,
что
на
самом
деле
транзистор
исправен?
3.
Расследуются
причины
неудачного
запуска
космической
ракеты,
о
котором
можно
высказать
четыре
предположения
(гипотезы)
Н
1
'Н
2
'Н
З
или
Н
4
•
Поданным
статистики
P(H
1
)=0,2,P(H
2
)=0,4,
.
Р(Н
3)
= 0,3,
Р(Н
4) =
0,1
.
В
ходе
расследования
обнаружено,
что
про
изошла
утечка
топлива
(событие
А).
Условные
вероятности
события
А
согласно
той
же
статистике
равны:
P(AIH
1
)=0,9,P(AIH
2
)=0,
Р(А/
Н
3) =
0,2,
Р(АI
Н
4) = 0,3.
Какая
из
гипотез
наиболее
вероятна
при
данных
условиях?
4.
Однотипные
приборы
выпускаются
тремя
заводами
в
количест
венном
отношении
1 :2:3,
причем
вероятности
брака
для
этих
заводов
соответственно
равны
3%, 2%, 1 %.
Прибор,
приобретенный
нау"чно-
82

исследовательским
инстmyтом,
оказался
бракованным.
Какова
вероят
ность
того,
что
этот
прибор
произведен
первым
заводом
(марка
завода
на
приборе
отсутствовала).
5.
Партия
деталей
изготовлена
тремя
рабочими,
причем первый
изго
товил
35%
всех
деталей,
второй
- 40%,
третий
-
всю
остальную
продук
цию.
Брак
в
их
продукции
составляет:
у
первого
- 2%,
У второго
- 3%,
У
третьего
- 4%.
Случайно
выбранная
для
контроля
деталь
оказалась
брако
ванной.
Найти
вероятность
того,
что
она
изготовлена
третьим
рабочим.
Ответы
1.1)
0,272; 2) 0,113; 3) 0,614.2.0,221.3.
Н
)
.4.0,3.5.0,345.
Глава
2.
Случайные
величины,
их
распределение
и
числовые
характеристики
§ 2.1.
Дискретные
и
непрерывные
случайные
величины.
Закон
распределения
дискретной
случайной
величины
Случайной
величиной
называют
переменную
величину,
которая
в
за
висимости
от
исходов
испытания
принимает
значения,
зависящие
от
случая
.
.
Случайная
величина,
при
ни
мающая
различные
значения,
которые
можно
записать
в
виде
конечной
или
бесконечной
последовательности,
называется
дискретной
случайной
величиной.
Случайная
величина,
которая
может
принимать
все
значения
из
не-
- - - -1
которого
промежутка,
называется
неnpерывнои
случаинои
величинои
.
Случайные
величины
будем
обозначать
заглавными
буквами
латин-
ского
алфавита
Х,
У,
z
...
,
а
их
значения
-
строчными
буквами
с
индекса-
ми,
например,
XI,
Х2, Хз,
..
.
Законом
распределения
дискретной
случайной
величины
называется
соответствие
между
значениями
XI,
Х2,
Хз,
...
этой
величины
и
их
вероят
НОСТЯМИРI,Р2,РЗ,
....
Закон
распределения
дискретной
случайной
величины
может
быть
задан
таблично
или
аналитически
(т.е.
с
помощью
формул).
Если
дискретная
случайная
величина
Х
принимает
конечное
множе
ство
значений
XI,
Х2,
... ,
хnсоответственно
С
вероятностями
PJ,
Р2,
...
,
Рn,
J
Более
точное
определение
непрерывной
случайной
величины
будет
дано
в
§ 2.2.
83

то
ее
закон
распределения
опредеjlЯется
формулами
P(X=Xk)=Pk
(k=I,2,
.
..
n),
Этот
закон
можно
задать
и
та(5лицей
(см.
табл.
2.1).
Х
Х2
Хз
Р
Р2
р
з
(2.
1.1
)
(2.1.2)
Таблица
2.1
рn
в
этой
таблице
сумма
вероятностей
также
равна
единице
:
РI
+
Р2
+
..
. +
Рn
= 1.
События
(Х
= X
k
),
k =
1,
2,
.
..
,
n,
образуют
полную
группу
событий,
поэтому
выполняется
равенство
(2.1.2).
для
наглядности
закон
распределения
дискретной
случайной
вели
чины
изображают
графически,
для
чего
в
прямоугольной
декартовой
системе
координат
строят
точки
(X
k
,
Pk)
И
соедиНЯJOТ
их
последова
тельно
отрезками
прямых.
Получающаяся
при
этом
ломаная
линия
на
зывается
МllогоугОЛЬНUКОАI
распределения
случайной
величины
Х.
Если
дискретная
случайная
величина
Х
принимает
бесконечную
по
следовательность
значений
XI,
Х2, Хз,
.
..
соответственно
с
вероятностями
PI,
Р2,
Рз
...
,
то
ее
закон
распределения
определяется
формулами
P(X=Xk)=Pk
(k=I,2,З,
...
),
(2.1.3)
(2.1.4)
Этот
закон
распределения
дискретной
случайной
величины
Х,
при
нимающей
бесконечную
последовательность
значений
XI,
Х2, Хз,
...
мож
но
задать
и
таблицей
(см.
табл
2.2).
Таблица
2.2
Х
ХЗ
Х"
Р
р
з
рn
Ряд
,
составленный
из
чисел
PI,
Р2,
Рз
...
таблицы
2.2
сходится
и
его
сумма
равна
единице.
3
а
м
е
ч
а
н и
е
.
Отличие таблицы
2.2
от
таблицы
2.1
состоит
в
том,
что
ВО
второй
таблице
нет
последнего
значения;
в
первой
таблице
оно
есть.
84

11
Р
и
м
е
р
1.
Задаю!
ли
законьi
распределения
дискретной
случайной
величины
следующие
таблицы?
а)'
б)
Х
2
3
4
5
Х
б
7
8 9
Р
0,1 0,4 0,3 0,2
Р
0,1 0,2 0,3 0,5
Реш
е н и
е.
Первая
таблица
задает
закон
распределения
дискретной
случайной
величины, поскольку
выполняется
равенство
(2.1.2):
0,1+0,4+0,3+0,2=1.
Вторая
таблица'
не
задает
закон
распределения
дискретной
случай-
ной
величины,
так как
условие
(2.1.2)
не
выполнено:
0',1+0,2+0,3+0,5=1,1'#1.
При
м
е р
2.
Задают
ли
следующие
таблицы
законы
распределения
дискретной
случайной
величины?
а)
Х
l/3
1/32
1/33
...
l/з
k
...
Р
l/2
l/2
2
1/23
...
l/2
k
...
б)
[ ;
1/4
1/2
1/3
l/k
Реш
е
н
и
е.
Первая
таблица
задает
закон
распределения
дискретной
случайной
величины
Х,
принимающеи
бесконечную
последовательность
значений
X
k
=
l/з
k
(k
=
1,
2,
3 ...
).
Действительно,
ряд
из
чисел
Pk
=
1I2
k
(k =
1,
2, 3 ... )
сходится
и
его
сумма
равна
единице;
это
гео-
Й
"aqk-I
1/2
метрически
ряд
вида
~
с
первым
членом
а
=
и
знаменате-
k~1
лем
q =
1/2:
Равенство
(2.1.4)
в
данном
случае
выполнено.
85
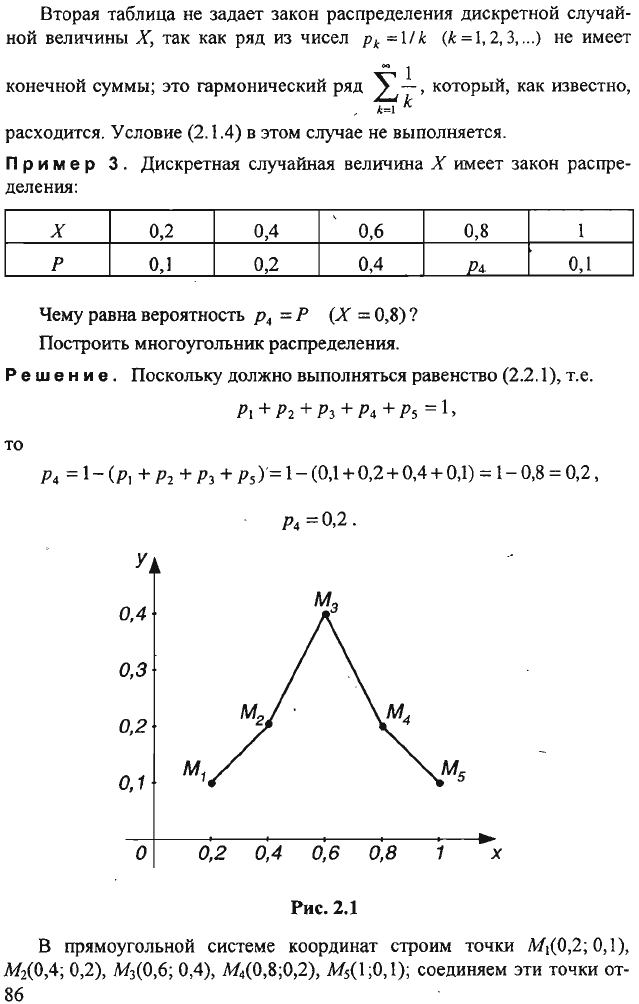
Вторая
таблица
не
задает
закон
распределения
дискретной
случай
ной
величины
Х,
так как
ряд
из
чисел
Р.
= 1/ k
(k
= 1,2,3,
...
)
не
имеет
~
1
конечной
суммы;
это
гармонический
ряд
L..
-,
который,
как
известно,
•
о=1
k
расходится.
Условие
(2.1.4)
в
этом
случае
не
выполняется.
При
м
е
р
З.
Дискретная
случайная
величина
Х
имеет
закон
распре
деления:
Х
0,4 0,2
l'
0,6
р
0,2
0,1
0,4
Чему
равна
вероятность
Р4
=
Р
(Х
= 0,8)?
Построить
многоугольник
распределения.
0,8
0,1
Ре
w
е н и
е.
Поскольку
должно
выполняться
равенство
(2.2.1),
Т.е.
РI
+
Р2
+
Рз
+
Р4
+ Ps = 1,
то
Р4
=
1-
(РI
+
Р2
+
Рз
+ ps)'=
1-
(0,1
+0,2+0.4+0,1)
=
1-
0,8 =
0,2,
Р4
=0,2.
У
0,4
0,3
0,2
0,1
М
1
О
0,2
0,4
0,6
0,8
1
х
Рис.
2.1
В
прямоугольной
системе
координат
строим
точки
M
1
(0,2; 0,1),
М
2
(0,4;
0,2),
М
з
(0,6;
0,4),
М
4
(0,8;0,2),
M
s
(1
;0, 1);
соединяем
эти
точки
от-
86

резками
прямых
(рис
2.1).
Ломаная
М'М
2
М
З
М
4
М
5
является
многоуголь
ником
распределения
данной
случайной
величины.
П"
и
м
е
р
4.
Дискретная
случайная
величина
Х
имеет
закон
распре
деления:
1;
1:,
1
:,15
5
1
:,25
1
:,35
Рз
Найти
вероятности
р,
=Р(Х
=3)
и
Рз
=Р(Х
=5),
если
известно,
что
Рз В
4
раза
больше
р,.
Реш
е
н
и
е.
Так
как
Р2
+
Р4
+
Ps
= 0,15 + 0,25 + 0,35 =
0,75,
то
на
основании
равенства
(2.1.2)
закmoчаем,
что
Р,
+
Рз
=
1-
0,75
=0,25
.
Поскольку
по
условию
Рз
= 4
РI
,
то
РI
+
Рз
=
РI
+ 4
РI
= 5
РI
.
Значит,
5
РI
= 0,25 ,
откуда
Р,
= 0,05 ;
следовательно,
Рз
=4р,
=4·0,05
=0,20.
Итак,
РI
= 0,05;
Рз
= 0,20 .
При
м
е р
5.
Подбрасываются
две
симметричные
монеты,
подсчиты
вается
число
гербов
на
обеих
верхних
сторонах
монет.
Рассматривается
дискретная
случайная
величина
Х
-
число
выпадений
гербов на
обеих
монетах.
Записать
закон
распределения
случайной
величины
Х.
Ре
ш
е
н
и
е.
В
данном
опыте
четыре
равновозможных
элементарных
исхода:
(Г,
N,
(Г,
Ц),
(Ц,
n,
(ц,
Ц);
запись
(Г,
Ц)
означает,
что на
первой
монете
выпал
герб,
на
второй
-
цифра;
аналогичный
смысл
имеют
ос
тальные
записи.
Герб
может
выпасть
1
раз,
2
раза
или
не
появиться
ни
разу.
Следовательно,
случайная
величина
Х
может
принимать
только
три
значения:
х,
=
О,
Х
2
=
1,
х
з
= 2 .
Найдем
вероятности
этих
значений:
1 2 1
Р(Х
=
О)
= - =
о
25·
Р(Х
=
1)
= - =
О
50·
Р(Х
= 2) = - =
О
25
.
4 ' ,
4'
,
4'
,
Р,
= 0,25,
Р2
= 0,50,
Рз
= 0,25 ;
87

причем,
р,
+
Р2
+
Рз
= 1 .
Таким
образом,
закон
распределения
данной
случайной
величины
можно
задать
таблицей
Х
О
2
Р
0,25 0,50 0,25
При
м
е
р
6.
Подбрасываются
два
игральных
кубика,
подсчитывается
число
очков,
выпавших
на
обеих
верхних
гранях.
Найти
закон
распреде
ления
дискретной
случайной
величины
Х
-
суммы
выпавших
очков
на
двух
игральных
кубиках.
Реш
е
н
и
е.
В
этом
испытании
36
равновозможных
элементарных
исходов
(см.
табл.
1.1).
Случайная
величина
Х
может
принимать
целые
значения от
2
до
12,
причем
значения
2
и
12
принимает
по
(}дному
разу,
3
и
11
-
по
2
раза,
4
и
1
О
-
по
3
раза,
5
и
9 -
по
4
раза,
6
и
8 -
по
5
раз,
значение
7 - 6
раз.
.
Вычислим
вероятности
этих
значений:
2 1 . 1
РIo
=
Р(Х
=
11)
= -
=-,
РII
=Р(Х
= 12)
=-.
36
18
36
Следовательно,
закон
распределения
данной
случайной
величины
Х
можно
задать
таблицей
Х
2 3
4
5 6
7 8
9
10
II
Р
1
1
1
1 5 1 5
1 1
1
-
-
- -
- - -
-
-
-
36
18
12 9 36 6 36 9
12 18
Отметим,
что
11115151111
-+-+-+-+.-+-+-+-+-+-+-
=1,
36
18
12 9 36 6 36 9 12
18
36
Т.е.
ВЫПОЛНеНО
равенство
(2.1.2).
88
12
1
-
36

При
м
е р
7.
В
коробке
7
карандашей,
из
которых
4
красные.
Из
этой
коробки
наудачу
извлекаются
3
карандаша.
Найти
закон
распределения
случайной
величины
Х,
равной
числу
красных карандашей
в
выборке.
Реш
е
н и
е.
В
выборке
из
трех
карандашей
может
не
оказаться
ни
одного
красного
карандаша,
может
появиться
один,
два
или
три
каран
даша.
Следовательно,
случайная
величина
Х
может
принимать
только
четыре
значения:
Х
1
=
О,
Х
2
=
1,
Х
з
= 2,
Х
4
= 3 .
Найдем
вероятности
этих
значений:
СО
.с
3
C
I
·C
2
12
р)=Р(Х=О)=
4
з
=
Р2
=
Р(Х
=
1)
= 4 3
=
с
3
35'
С
З
35'
7
7
с
2
·с)
18
с;
·C~
4
Рз
=Р(Х
=2)=
4 3
=
Р4
=Р(Х
=3)
=
-
с
3
35 '
с
3
35
7
7
Следовательно,
данная
случайная
величина
Х
имеет
закон
распреде
ления:
Х
о
1
35
12
35
2
18
35
3
4
35
Отметим,
что
1/35+
12/3
5 +
18/3
5
+4/35
= 1,
т.е.
выполнено
равен
ство
(2.1.2).
При
м
е
р
8.
Вероятность
изготовления
нестандартного
изделия
при
некотором
технологическом
процессе
равна
0,06.
Контролер
берет
из
партии
изделие
и
сразу
проверяет
его
качество.
Если
оно
оказывается
нестандартным,
дальнейшие
испытания
прекращаются,
а
партия
задер-
.
живается.
Если
же
изделие
оказывается
стандартным,
контролер
берет
следующее
и
т.д.,
но
всего
проверяет
не
более'ПЯТИ
изделий.
Найти
за
кон
распределения
дискретной
случайной
величины
Х
-
числа
проверяе
мых
изделий.
Реш
е
н
и
е.
ДИскретная
случайная
величина
Х
может
принимать
пять
значений:
Х
1
=
1,
Х
2
= 2,
Х
З
=
3,
Х
4
= 4, X
s
=
5.
Она
примет
значение
Х)
= 1 ,
т.е.
будет
проверено
лишь
одно
изделие
и
партию
задержат,
если
первое
проверенное
контролером
изделие
окажется
нестандартным.
Ве
роятность
такого
исхода
испытания
Р(Х
=
1)
=
0,06.
Проверяют
два
изделия,
т.е.
Х=2,
если
первое
окажется
стандарт
ным,
а
второе
-
нестандартНым.
Вероятность
такого
исхода
испытания
89

найдется
по
теореме
умножения:
Р(Х
= 2) = 0,94·0,06"" 0,056
(здесь
0,94 = 1 - 0,06 -
вероятность
того,
что
изделие
окажется
стандартным).
Испытание
ограничится
проверкой
качества
трех
изделий,
если
пер
вые
два
окажутся
стандартными,
а
третье
-
нестандартным.
По
теореме
умножения
вероятность
такого
исхода
испытаний
Р(Х
=
3)
= 0,942·0,06
""
""
0,053.
Аналогично
находим
Р(Х
= 4) = 0,943' 0,06
""
0,50.
Проверяются
пять
изделий,
если
первые
четыре
окажутся
стандарт
ными,
так
как
при
любом
качестве
пятого
изделия
по
условию
проверка
партии
заканчивается.
Имеем
Р(Х
s::
5)
= 0,944
""
0,781.
3
а
м
е
ч а
н
и
е.
Тот
же
результат
можно
получить
и
другим
способом.
Пять
изделий
проверяются
в
двух
СJIYчаях,
которые
являются
несовместными
событиями:
1)
первые
четыре
изделия
окажугся
стандартными
и
пятое
также
cтaRЛaPТHbL'd;
2)
первые
четыре
изделия
окажугся
стандартными,
а
пятое
-
не
стандартным.
Вероятности
этих
случаев
по
теореме
умножения
для
независи-
мых
событий равны
0,944 ·0,94
и
0,944·0,06,
а
поэтому,
в
соответствии
с
тео
ремой
сложения,
вероятность
того,
что
контролер
будет
проверять
пять
изде
лий,
определится
так:
Р(Х
=
5)
= 0,944 ·0,94 + 0,944 ·0,06 = 0,944 . (0,94 + 0,06) = 0,944
'"
0,781.
Следовательно,
закон
распределения
рассматриваемой
случайной
величины
Х
можно
представить
в
следующем
виде:
Х
2 3
4
5
Р
0,06 0,056
0,053
0,050 0,781
Отметим,
что
0,06+0,056+0,053+0,050+0,781=1,
Т.е.
выполнено
ус
ловие
(2.1.2).
11
Р и
м
е р
9.
Производится
серия
независимых
опытов,
в
каждом
из
которых
наступает
событие
А
с
одной
и
той
же
вероятностью
р.
Опыты
продолжаются
до
первого
появления
события
А.
Рассматривается
слу
чайная
величина
Х
-
число
произведеннъrх
опытов.
Составить
для
нее
закон
распределения.
Реш
е
н
и
е.
Указанная
случайная
величина
Х
может
принимать
зна
чения
Х
1
=1'X
2
=2,х
з
=3,
....
Событие
Х=n
(n=1,2,3,
...
)
означает,
что
в
первых
n-l
опытах
событие
А
не
наступает,
а в
n-м
наступает.
Вероятност~
такого
исхода
равна:
11-1
q.q
.....
q.p=pq,
'-v----'
11-1
раз
где
q =
1-
р.
Следовательно,
закон
распределения
данной
случайной
90
