Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

352

ГЛАВА 1 г

продолжается, и в случае подходящей разбивки можно использовать бло-

кирование по двум признакам [287].

Ниже в качестве примера описывается подобный эксперимент, целью

которого была изоляция погрешности, вносимой повторными определениями

бора в образцах осадочных пород; такая проблема возникла после того, как

было обнаружено, что различные навески из одной и той же массы тонко-

измельченного осадка дают слишком расходящиеся результаты. Содержание

бора было выбрано в качестве интересующей нас случайной величины X

liz

представляемой в частях на миллион.

Тридцать образцов представлены десятью определениями на каждой

из пяти пластинок, т. е. всего имеем 50 определений. При таком распределе-

нии данных (табл. 20.7) можно заметить, что имеется два класса C

буквенных

Таблица 20.7

Выборочная разбивка по принципу «цепные блоки»

с тридцатью ступенями

Полосы равны блокам

Число образцов на

полосе

Блок

Класс

Число образцов на

полосе

3 4 5

Класс

1¾

=20

{

I +

2 =

= 30 ступен

ей = об

разцов

Щ + 2

= 50

символов; 20 прописных букв от А до T (C

), которые встречаются дважды,

и 10 строчных букв от а до т (C

), которые встречаются один раз. Обозначим

через tij

эффект и-й обработки ;-й группы C

, а через b

—

эффект z-ro блока.

Тогда структура эксперимента выразится так [79, 462]:

Xija ^ hill. +

+ г

. (20.4)

Предполагается, что tij

изменяются случайно со средним 0 и диспер-

ί σ

, а ε

iju

не з

измерений. Если

сиеи σ

, а ε

не зависит от случайных изменений, связанных с производством

П2

XHζ = 2

X-21UZ

и Dj = X

Jj = XiHi+

1)>

и=1

то iuj определяется в нашем случае как

i = l, 2; / = 1, ..., 5;

= 1,

i = i,

i = 2.

ί 20,

" =I 10,

и и означает определение ;-и группы г-го класса.

ПРОЧИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕШЕНИЯ 353·

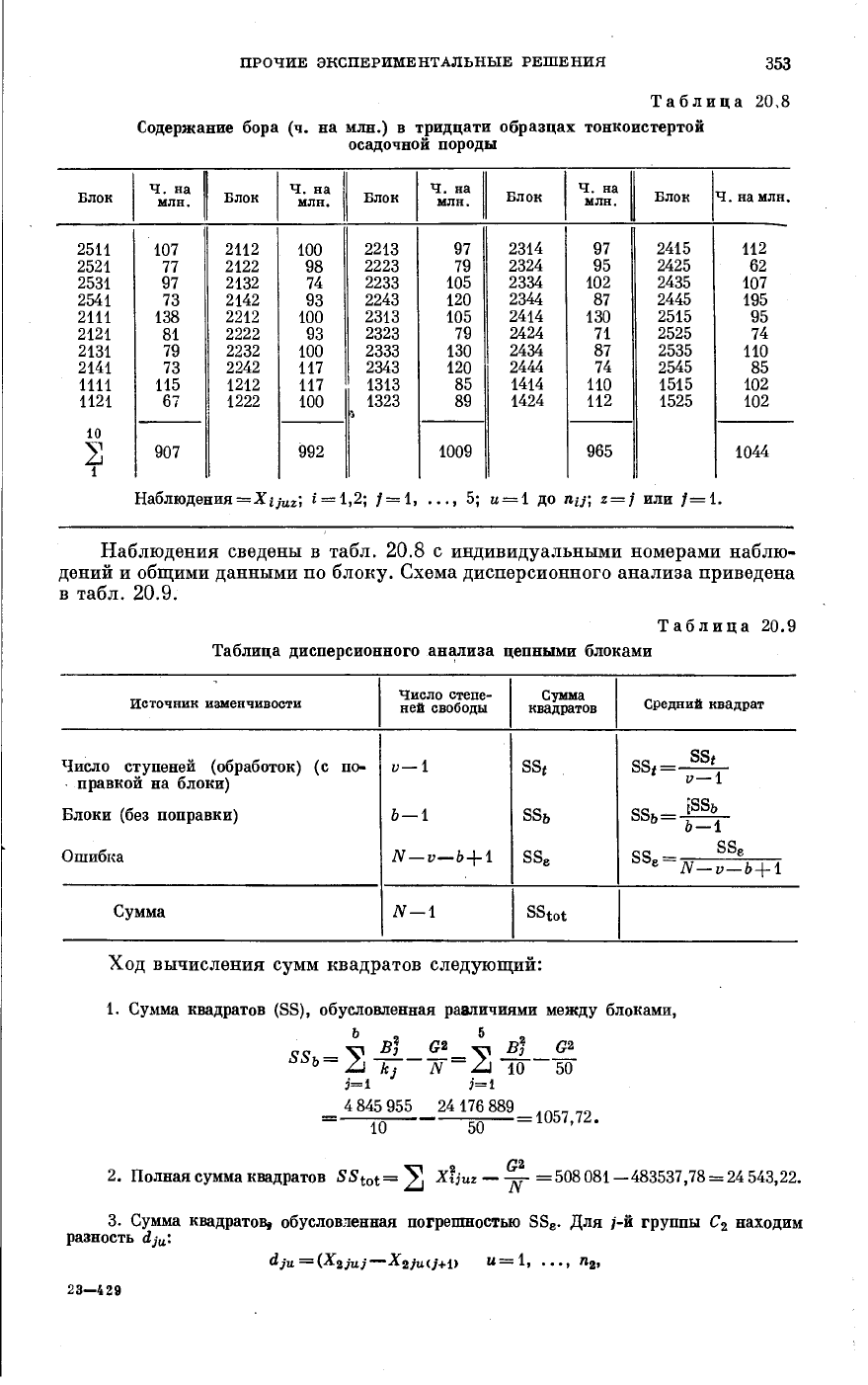
Таблица 20,8

Содержание бора (ч. на млн.) в тридцати образцах тонкоистертой

осадочной породы

Блок

Ч. на

млн.

Блок

Ч. на

млн.

Блок

Ч. на

млн.

Блок

Ч. на

млн.

Блок Ч. на млн.

2511

2521

2531

2541

2111

2121

2131

2141

1111

1121

107

138

115

2112

2122

2132

2142

2212

2222

2232

2242

1212

1222

100

117

100

2213

2223

2233

2243

2313

2323

2333

2343

1313

1323

105

120

105

130

120

2314

2324

2334

2344

2414

2424

2434

2444

1414

1424

102

130

110

112

2415

2425

2435

2445

2515

2525

2535

2545

1515

1525

112

107

195

110

102

907 992

1009

965

1044

Наблюдения = Xij

·, i — 1,2; / = 1, ..., 5; и

— 1

до пц; z = j или /=1.

Наблюдения сведены в табл. 20.8 с индивидуальными номерами наблю-

дений и общими данными по блоку. Схема дисперсионного анализа приведена

в табл. 20.9.

Таблица 20.9

Таблица дисперсионного анализа цепными блоками

Источник изменчивости

Число степе-

ней свободы

Сумма

квадратов

Средний квадрат

Число ступеней (обработок) (с по-

правкой на блоки)

Блоки (без поправки)

Ошибка

υ— 1

Ъ — 1

Ν—ν—6+1

SSt

ν— 1

CQ SSg

Ь8в-

лг—6+1

Сумма

Ν — 1

SStot

Ход вычисления сумм квадратов следующий:

1. Сумма квадратов (SS), обусловленная различиями между блоками,

„„

, G2

в} G»

bi>b=

2j-k]— ^v=ZJ ТО™50

3=1 J=I

4845 955 24 176 889

10 50

-=1057,72.

ΛΟ

2. Полная сумма квадратов SS

tot

= ^

Ьиг — =508 081 —483537,78 = 24 543,22.

3. Сумма квадратов, обусловленная погрешностью SS

. Для /-й группы C

находим

разность dj

dju = (Xijuj—1) и= 1, ..., л

23—429

354

ГЛАВА 1 г

например:

^ii = AT

2111

-X

2113

= 138—100 = 38;

^12

= -^2121—^2122 = ^1—98= —17;

^13=-^2123—-^2132 = 79

—

74 = 5;

^14

^2141 — -^2142==73 —

93= —20.

Тогда

4 4 4 S 4

2 d

= 6, 2

2u = 9, 2

= 53, 2 =-144, 2

SU=IO;

U= 1 1 1 u=l 4-1

также

4 4 4

= 2158, 2 ^lu=239, 2

Iu = 2193,

«=1 u=l u=l

•

4 5

2¾ =15 446, ^dl

= 466.

1 1

Тогда сумма квадратов, обусловленная погрешностью, оудет SS

, где

712 712 712

, ,=-1 2 [Σ ^)

U=I 1 1

например:

4 4

SSe,

= 1 [ 2 ( Σ <Ц

] =4 [2158-1 (62)] = 1074,5,

ti= 1 u=l

и аналогично SS

= 109,375, SS

8j3

= 745,375, SS

= 6098,5 и SS

= 220,5. Полная SS

J = 8248,50. Теперь SS

,у является оценкой суммы

квадратов, обусловленной погрешностью с числом степеней свободы п

— 1.

Вычислением аналогичного числа для каждой группы C

находим сумму

квадратов, обусловленную погрешностью с числом степеней свободы b (п

—

— 1) = 15. Остающиеся степени свободы определяются выражением

Ь Ь 5 5

у =

26^ ( Σ *2Z(

Z+

1, - 2 = 2x5x4 ( Σ

W"- Σ =

2=1 2=1 2=1 2=1

= 1 [(1977— 1941)]2

—

32,4.

Тогда

= 2 SS

, У = 8 280,650.

J=I

4. Обработка полученных сумм квадратов.

= SStot - SS

- SS

= 16 279,35.

Результирующий дисперсионный анализ дается в табл. 20.10. Проверка

процедур на погрешность представляет основной интерес и критическое

значение F в условиях гипотезы H

отсутствия различий между средними

по каждой обработке будет F

э, ιβ

2,28; наблюдаемое же значение F =

= 1,01, так что причин отвергать гипотезу нет и, следовательно, нет и раз-

личий между средними. Судя по полученному результату с его относительно

большим остаточным членом, едва ли можно повторить анализ. Нужно иметь

ПРОЧИВ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕШЕНИЯ 355

Таблица 20.10

Дисперсионный анализ содержания бора (ч. на млн.)

Источник изменчивости Число степеней свободы

Сумма квадра-

тов

Средний квадрат

Число ступеней (обработок)

(с поправкой на блоки)

Блоки (без поправки)

Ошибка

у—1 = 29

—

1=4

Ν— υ—6+1 = 16

15 204,85

1 057,72

8 280,65

524,305

264,48

517,54

Сумма

TV-1 = 49

24 543,22

524,305 ,

SST= 517,540

"Ρ* iv—г—b+i·

какие-то гарантии для получения уверенности в том, что повторные пробы

анализируемых порошков окажутся также однородными. Воспроизводи-

мость анализов в дальнейшем проверялась аналогичным способом.

Когда достигнут желаемый уровень точности воспроизводимости ана-

лизов, цель эксперимента меняется: теперь она заключается в сравнении

средних по выборкам, и тогда становится необходимым вычислить соответ-

ственный остаточный член. Это можно сделать тремя способами и каждый

основан на своей погрешности:

1. Сравнение между любыми двумя средними в C

, скажем и ti

> где

Var(huj-hsw) = [/ (0+ (

+ ^")]°

i = j — s (mod Ъ).

2. Сравнение двух средних в C

, скажем t

и I

2szv

, где

, Var(^

-W)= {^

)]σ2;

3. Сравнение двух средних в C

и C

соответственно, скажем t\j

и Z

2su

,, где

1 ί

, 6— 1'

Var (tij

— t

sw) " <

(

)

[/(0+|(i-

σ»,

b + l-ii'

ηφ

Γ-

)]

, / Φ s,

i' = j—s [mod(Ь-f 1)];

/W =

(2ζ— 1) b—2ζ

ηφ

Должно быть ясно, что эти сравнения провести не столь легко, как при сим-

метричном полном способе, например при способе рандомизированных блоков,

и если остаточный член действительно не мал, то различия между средними

значениями могут остаться не выявленными. Применяя специальные методы

обработки такого рода, очень важно убедиться, что все условия их примене-

ния выполнены, иначе эксперимент окажется не вполне информативным.

23»

Г Л А В А 21

Измерение зависимости между переменными

Если для совокупности мы можем найти математическое выражение,

которое адекватно представляет имеющиеся данные, а затем по втим

данным вычислить наилучшие оценки нужных параметров, то обычно

считают, что получено все или почти все, что можно было бы извлечь

из имеющегося материала, вся доступная информация.

R. A. Fisher, Statistical Methods for Research Workers, Oliver

and Boyd, Ltd., IOth ed., p. 7, 1948

21.1. ВВЕДЕНИЕ

В большинстве случаев аналитические процедуры, описанные в пре-

дыдущих главах, заключаются в операциях с изменчивостью одной случайной

величины, однако чаще всего для каждого множества образцов измеряется

более одной переменной, причем возникает проблема выявления зависимости

между этими переменными. Здесь можно оперировать двумя видами моделей;

с помощью первой рассматривают преимущественно формы связи, со второй —

силу связи между переменными. В первом случае, при изучении формы связи

берут выборку значений случайной переменной (X

; i = 1, 2, . . ., к) и затем

измеряют значения другой переменной Y, определяемой совместно с пере-

менной X на определенном уровне. Такая модель называется регрессионной.

Когда обе переменные изменяются случайно, речь должна идти о степени

связи, или о второй модели, в которой более существенную роль играет мера

корреляции. Обе модели могут быть расширены, например, от простой линей-

ной регрессии, или корреляции к множественной регрессии и корреляции

и от линейной связи к нелинейной.

Так как многие нелинейные связи посредством соответствующих преоб-

разований могут быть сведены к линейным (см. ниже), такой вид регрессии

будет описан подробно. Для более широкого ознакомления с множественными

и нелинейными связями отсылаем читателя к известным руководствам [27,

44, 341], геологические примеры см. у Гриффитса [165, 167, 172, 176] и у Мил-

лера и Кана [299].

21.2. НЕКОТОРЫЕ ЗАВИСИМОСТИ МЕЖДУ ПЕРЕМЕННЫМИ

И ИХ ЛИНЕЙНОЕ ПРЕДСТАВЛЕНИЕ

Линейная зависимость между переменными может быть выражена

уравнением

Y = α + βΧ, (21.1)

где β — мера изменения Y на единицу изменения X, а α — отрезок, или

интервал, отсекаемый линией регрессии на оси У. Линейные регрессии,

ИЗМЕРЕНИЕ ЗАВИСИМОСТИ МЕЖДУ ПЕРЕМЕННЫМИ

357

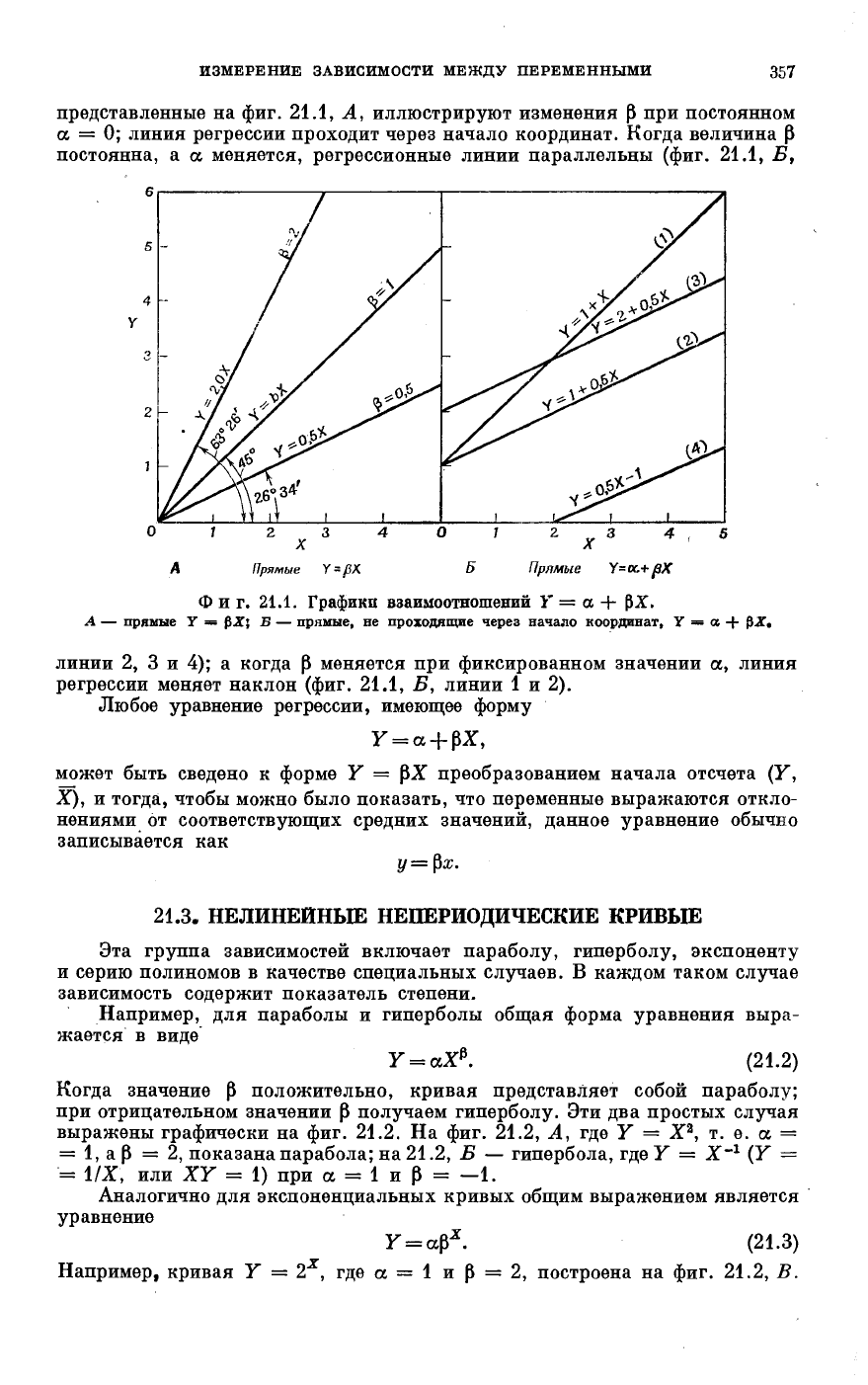
представленные на фиг. 21.1, А, иллюстрируют изменения β при постоянном

α = 0; линия регрессии проходит через начало координат. Когда величина β

постоянна, а α меняется, регрессионные линии параллельны (фиг. 21.1, Б,

А Прямые Y-βΚ Б Прлмые

Y=OC+

βΧ

Фиг. 21.1. Графика взаимоотношений У = а + βΧ.

А — прямые Y = ЭЛГ; Б — прямые, не проходящие через начало координат, У = а + β·Γ·

линии 2, 3 и 4); а когда β меняется при фиксированном значении а, линия

регрессии меняет наклон (фиг. 21.1, Б, линии 1 и 2).

Любое уравнение регрессии, имеющее форму

Y = α + βΧ,

может быть сведено к форме Y = βΧ преобразованием начала отсчета (У,

X), и тогда, чтобы можно было показать, что переменные выражаются откло-

нениями от соответствующих средних значений, данное уравнение обычно

записывается как

У = Px-

21.3. НЕЛИНЕЙНЫЕ НЕПЕРИОДИЧЕСКИЕ КРИВЫЕ

Эта группа зависимостей включает параболу, гиперболу, экспоненту

и серию полиномов в качестве специальных случаев. В каждом таком случае

зависимость содержит показатель степени.

Например, для параболы и гиперболы общая форма уравнения выра-

жается в виде

У = CtX

. (21.2)

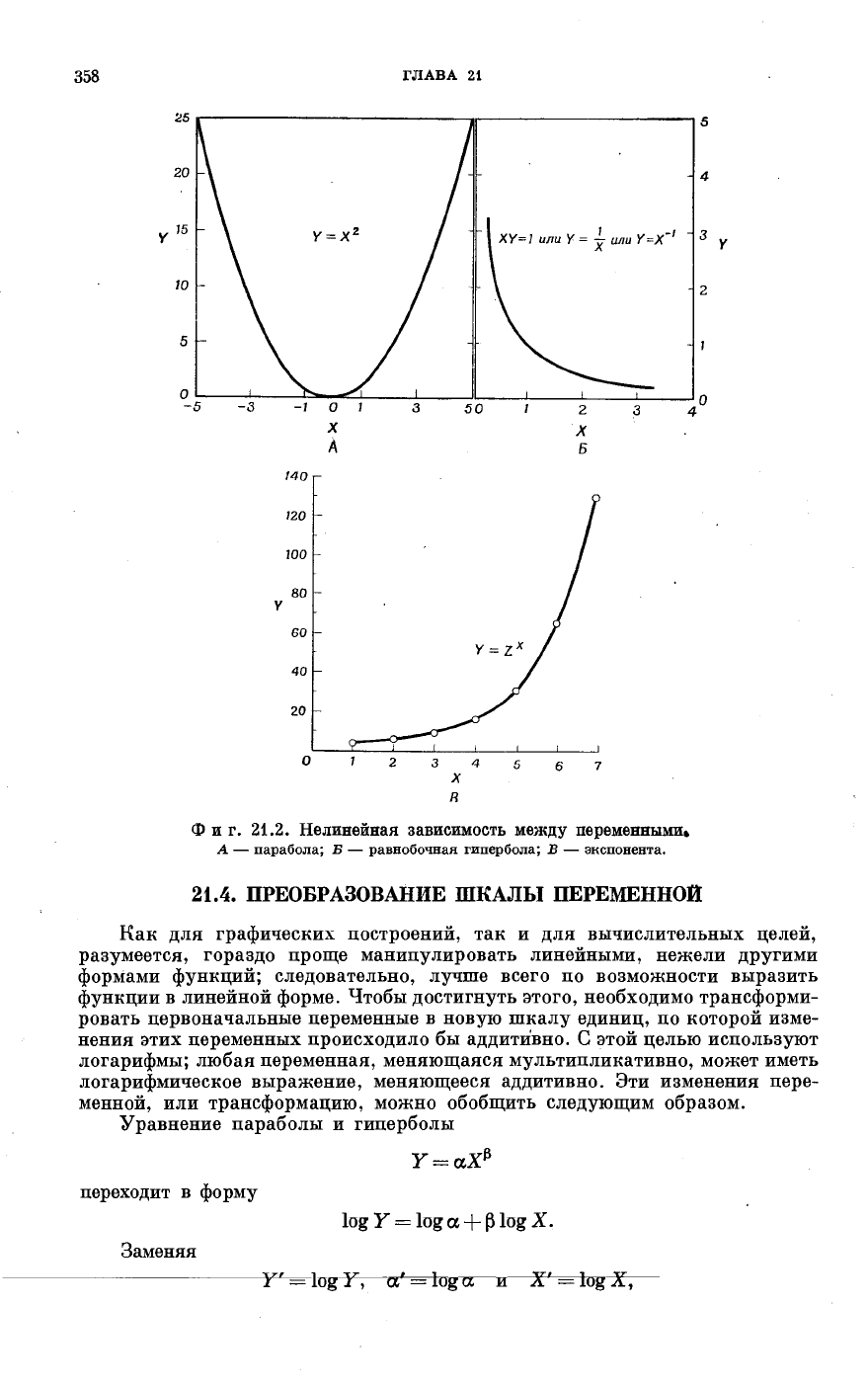
Когда значение β положительно, кривая представляет собой параболу;

при отрицательном значении β получаем гиперболу. Эти два простых случая

выражены графически на фиг. 21.2. На фиг. 21.2, А, где У = X

, т. е. α =

= 1, а β = 2, показана парабола; на 21.2, Б — гипербола, где У = X

-1

(У =

= 1/Х, или XY = 1) при α = 1 и β = —1.

Аналогично для экспоненциальных кривых общим выражением является

уравнение

Y = αβ*. (21.3)

Например, кривая У = 2

, где α = 1 и β = 2, построена на фиг. 21.2, В.

358

ГЛАВА 1 г

X X

А Б

Фиг. 21.2. Нелинейная зависимость между переменными»

А — парабола; Б — равнобочная гипербола; В — экспонента.

21.4. ПРЕОБРАЗОВАНИЕ ШКАЛЫ ПЕРЕМЕННОЙ

Как для графических построений, так и для вычислительных целей,

разумеется, гораздо проще манипулировать линейными, нежели другими

формами функций; следовательно, лучше всего по возможности выразить

функции в линейной форме. Чтобы достигнуть этого, необходимо трансформи-

ровать первоначальные переменные в новую шкалу единиц, по которой изме-

нения этих переменных происходило бы аддитивно. С этой целью используют

логарифмы; любая переменная, меняющаяся мультипликативно, может иметь

логарифмическое выражение, меняющееся аддитивно. Эти изменения пере-

менной, или трансформацию, можно обобщить следующим образом.

Уравнение параболы и гиперболы

Y = αΧ

переходит в форму

log Y = log α +

log Χ.

Заменяя

= log Υ, a' = Ioga и X

= IogX,

ИЗМЕРЕНИЕ ЗАВИСИМОСТИ МЕЖДУ ПЕРЕМЕННЫМИ

359

получаем

У' = α' + βΧ'.

Для экспоненциальной кривой

Y = αβ*

получаем

log У = Iog α+ X log β,

или

У' = α' + β'Χ.

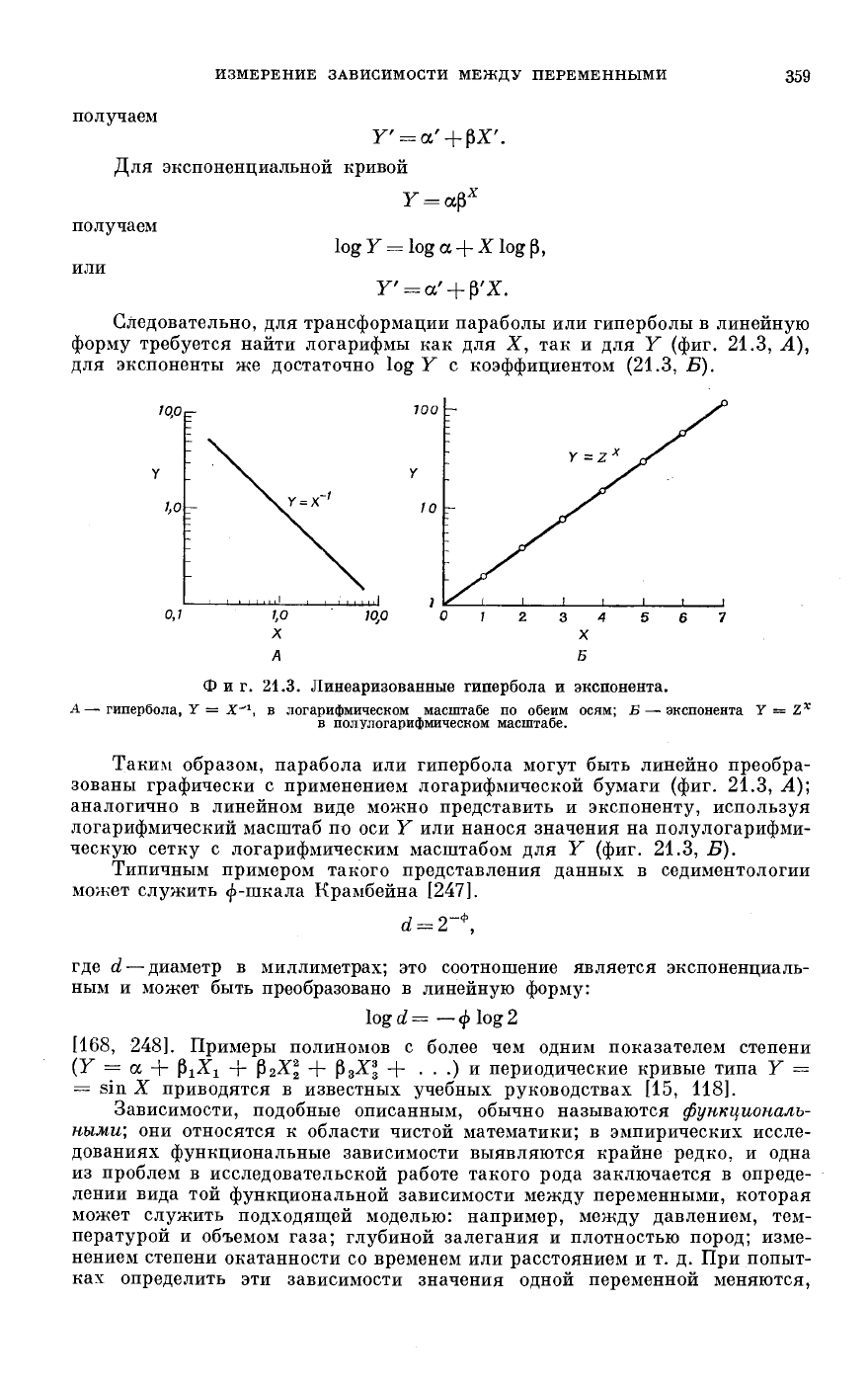
Следовательно, для трансформации параболы или гиперболы в линейную

форму требуется найти логарифмы как для X, так и для Y (фиг. 21.3, А),

для экспоненты же достаточно log Y с коэффициентом (21.3, Б).

х χ

Л Б

Фиг. 21.3. Линеаризованные гипербола и экспонента.

А — гипербола, Y = X^

, в логарифмическом масштабе по обеим осям; Б — экспонента Y = Z

в полулогарифмическом масштабе.

Таким образом, парабола или гипербола могут быть линейно преобра-

зованы графически с применением логарифмической бумаги (фиг. 21.3, А)',

аналогично в линейном виде можно представить и экспоненту, используя

логарифмический масштаб по оси Y или нанося значения на полулогарифми-

ческую сетку с логарифмическим масштабом для Y (фиг. 21.3, Б).

Типичным примером такого представления данных в седиментологии

может служить ψ-шкала Крамбейна [247].

d = 2~

где d— диаметр в миллиметрах; это соотношение является экспоненциаль-

ным и может быть преобразовано в линейную форму:

log d =

—

φ log 2

[168, 248]. Примеры полиномов с более чем одним показателем степени

(У =

ос

βι-Χχ + βгХ\ + β3X3 + . . .) и периодические кривые типа У =

= sin X приводятся в известных учебных руководствах [15, 118].

Зависимости, подобные описанным, обычно называются функциональ-

ными', они относятся к области чистой математики; в эмпирических иссле-

дованиях функциональные зависимости выявляются крайне редко, и одна

из проблем в исследовательской работе такого рода заключается в опреде-

лении вида той функциональной зависимости между переменными, которая

может служить подходящей моделью: например, между давлением, тем-

пературой и объемом газа; глубиной залегания и плотностью пород; изме-

нением степени окатанности со временем или расстоянием и т. д. При попыт-

ках определить эти зависимости значения одной переменной меняются,

360

ГЛАВА 1 г

а значения другой определяются экспериментально. Так, скажем, петрограф

оценивает окатанность галек на пляже на расстоянии одной, двух и трех миль

от некоторого базиса. Результаты он вычерчивает в виде графика, затем

пытается усмотреть в этом графике отражение некоторой функциональной

зависимости. Однако в таких эмпирических определениях, несомненно,

содержится погрешность, с которой измеряется изучаемая величина. Ведь

разные гальки, которые измеряются на протяжении трех миль, не будут

характеризоваться одной и той же степенью окатанности. С другой стороны,

при функциональной зависимости имеется в виду, что обе переменные заме-

рены без погрешности. Но в экспериментальных примерах изменяемая

переменная рассматривается как измеряемая без погрешности; она назы-

вается независимой переменной Х\ другая же переменная является случай-

ной, она дает различные значения при одном и том же значении независимой

переменной и называется зависимой переменной Υ.

Получив на образцах серию замеров двух переменных, можно наносить

эти результаты на график и изучать возможность определения формы функ-

ции. В общем случае последняя может оказаться линейной или быть одной

из функций, описанных ранее, и в этом случае ее можно свести к линейной

форме, применив подходящее преобразование. После этого следует согла-

совать кривую с изменениями, представленными на графиках; используе-

мая для этого процедура известна под названием метода наименьших квад-

ратов (впервые этот метод описали Лежандр и Гаусс, см. в работе [452].)

21.5. ОПРЕДЕЛЕНИЕ ЛИНИИ «НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ»

МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ

Имея набор замеров двух характеристик, или свойств на η образцах,

одно из которых (X) измерено без погрешности и каждому значению которого

соответствует множество определений другого свойства (Yi), мы можем

рассматривать совокупность Y-ов по каждому значению X и оценивать их

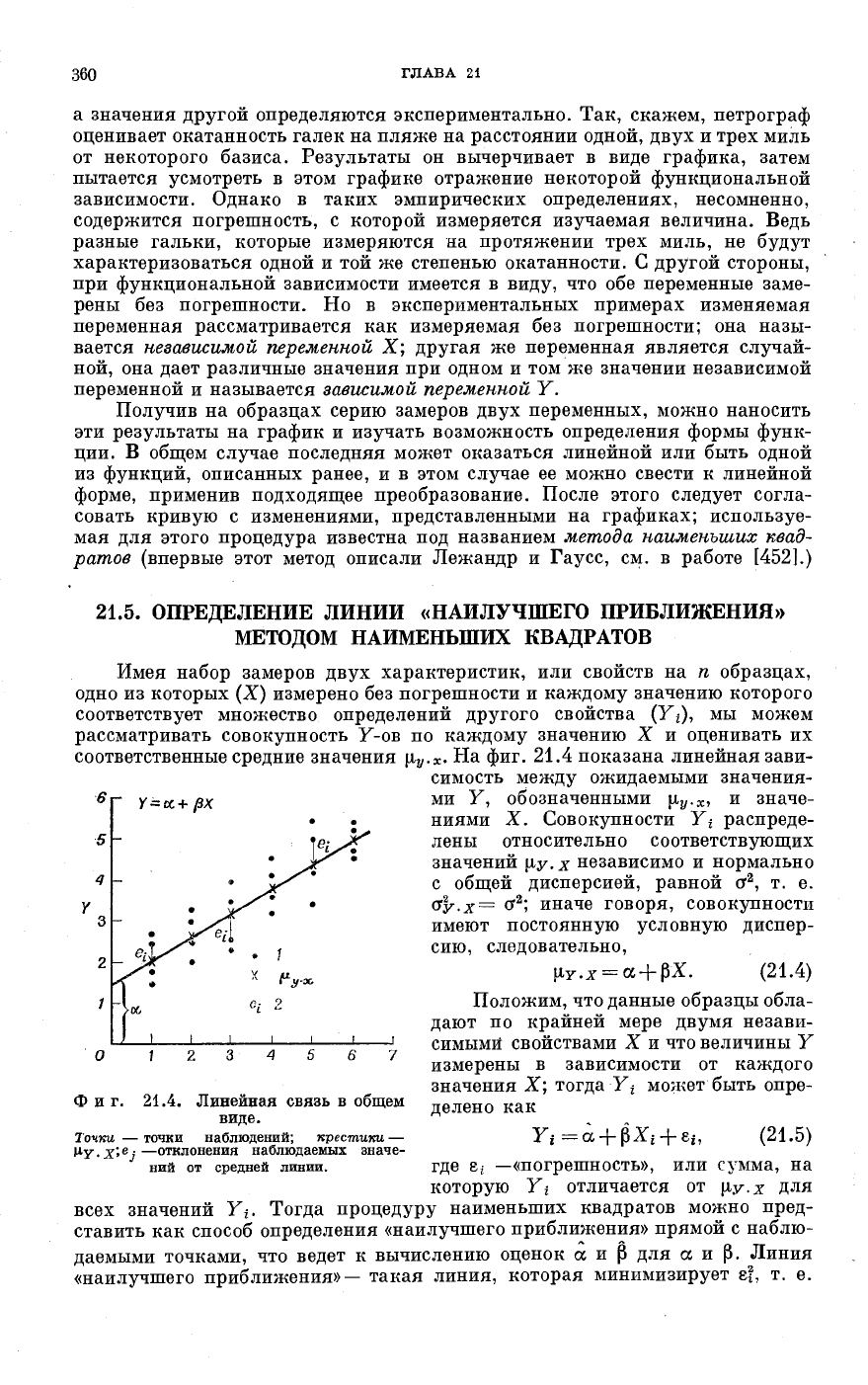
соответственные средние значения μ^.χ. На фиг. 21.4 показана линейная зави-

симость между ожидаемыми значения-

ми Y, обозначенными μ

, и значе-

ниями X. Совокупности Y

распреде-

лены относительно соответствующих

значений μy. χ независимо и нормально

с общей дисперсией, равной о

, т. е.

Gy.χ= σ

; иначе говоря, совокупности

имеют постоянную условную диспер-

сию, следовательно,

μγ.χ = α + ρΧ. (21.4)

Положим, что данные образцы обла-

дают по крайней мере двумя незави-

симыми свойствами X и что величины Y

измерены в зависимости от каждого

значения Х\ тогда Y

может быть опре-

делено как

Γ,^ + βΧί + β,, (21.5)

Фиг. 21.4. Линейная связь в общем

виде.

Точки — точки наблюдений; крестики

—

μγ.

x'.fj

—отклонения наблюдаемых значе-

ний от средней линии. где ε

;

—«погрешность», или сумма, на

которую Y

отличается от μ,ν.χ для

всех значений Y

. Тогда процедуру наименьших квадратов можно пред-

ставить как способ определения «наилучшего приближения» прямой с наблю-

даемыми точками, что ведет к вычислению оценок α и β для α и β. Линия

«наилучшего приближения»— такая линия, которая минимизирует ε?, т. е.

ИЗМЕРЕНИЕ ЗАВИСИМОСТИ МЕЖДУ ПЕРЕМЕННЫМИ 361

минимизирует квадратичное отклонение каждой величины Y

от соответ-

ствующего ей значения μ^^.χ. Тогда

и мы минимизируем

ε? = [Y

-{a + Px

)]

;

или, суммируя по всем X

Σ ε?= 2 [Г

+ рХ

)]

· (21.6)

1=1 i=l

Минимизацией этого выражения находим наилучшую оценку а для а

и β для β. Чтобы минимизировать, положим, что

и найдем частные производные Q соответственно по α и β (где производная

суммы есть сумма производных) и приравняем эти производные нулю:

да, ^

mmi

Это дает «нормальные уравнения»

= X,·, (21.7)

t=l t=l

53 X

= а 2 Χι +β Σ Xl (21.8)

i=l i=l i=l

Решение этих систем уравнений и дает искомые наилучшие оценки для α и β.

Вычислив ΣΧί, ΣХ\, Σ Y

, ΣΥ\, 2Х

, просуммировав от

до η

и подставив соответствующие значения в равенства (21.7) и (21.8), получим

значение α и β. Для решения данной системы уравнений существует несколько

процедур (см., например, работы [27] или [44]). Допустим, мы преобразуем

наши данные в отклонения от соответствующих им средних значений сле-

дующим образом:

= X

-X,

откуда

2*!=О,

тогда

У '-=Yt-Y, откуда Σ У ι = 0

Sti = 2 (Xf- X)

-2 Xi -

ί)2

, (21.9)

sy\= 2 (Y

-Y)* = 2

I-

(Σ

5 > (

°)

= 2 (Xi - Χ) (Yi -Y) = 2

^ -

' . (21.11)