Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

332

ГЛАВА 1 г

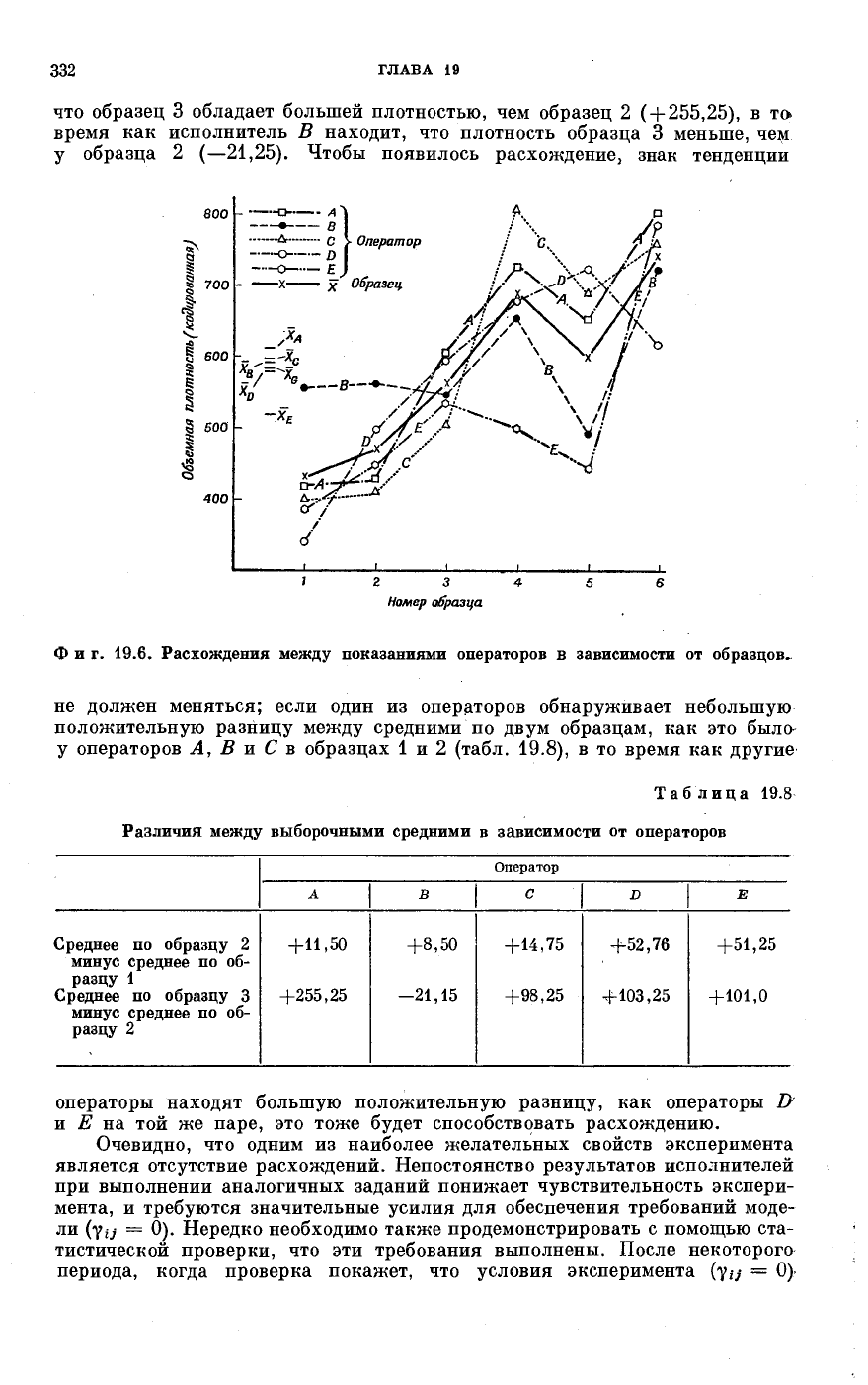
что образец 3 обладает большей плотностью, чем образец 2 (+255,25), в то

время как исполнитель В находит, что плотность образца 3 меньше, чем

у образца 2 (—21,25). Чтобы появилось расхождение, знак тенденции

Номер образца

Фиг. 19.6. Расхождения между показаниями операторов в зависимости от образцов..

не должен меняться; если один из операторов обнаруживает небольшую

положительную разницу между средними по двум образцам, как это было-

у операторов А, В и С в образцах 1 и 2 (табл. 19.8), в то время как другие

Таблица 19.8

Различия между выборочными средними в зависимости от операторов

Оператор

А в С

Среднее по образцу 2

минус среднее по об-

разцу 1

Среднее по образцу 3

минус среднее по об-

разцу 2

+11,50

+255,25

+8,50

-21,15

+14,75

+98,25

+52,76

+103,25

+51,25

+101,0

операторы находят большую положительную разницу, как операторы D

и £ на той же паре, это тоже будет способствовать расхождению.

Очевидно, что одним из наиболее желательных свойств эксперимента

является отсутствие расхождений. Непостоянство результатов исполнителей

при выполнении аналогичных заданий понижает чувствительность экспери-

мента, и требуются значительные усилия для обеспечения требований моде-

ли (= 0). Нередко необходимо также продемонстрировать с помощью ста-

тистической проверки, что эти требования выполнены. После некоторого

периода, когда проверка покажет, что условия эксперимента = 0).

ОДНОФАКТОРНЫЙ

ДИСПЕРСИОННЫЙ АНАЛИЗ

333

в достаточной мере выполняются, это позволит обходиться без текущей про-

верки. Иначе говоря, классификация по двум признакам с повторениями

необходима, по крайней мере

вначале, а классификация по

двум признакам без повторе-

ний и без выполнения тре-

бования y

j = 0, вероятно,

приведет к заблуждениям.

8 OO

§ 700

600

500

S 400 -

19.8. ОЦЕНКИ КОМПО-

НЕНТ ДИСПЕРСИИ

Основное назначение

данного эксперимента — оцен-

ка значений изменчивости,

вносимой соответствующими

причинами, и рекомендации

к дальнейшим эксперимен-

там. Следует снова заметить,

что совокупности, для кото-

рых изучаются α·

· и бед),

бесконечны по объему, поэто-

му в основе подобного ана-

лиза лежит модель бесконечной совокупности. При такой модели компо-

ненты дисперсии, соответствующие каждому источнику изменчивости, можно

оценить по вычисленным средним квадратам. Говоря точнее, наблюдаемые

средние квадраты являются несмещенными оценками ожидаемых сред-

них квадратов [385]. Эти вычисления производятся непосредственным спо-

собом; так, по табл. 19.6 средний квадрат ошибки

σ%

равен 8,247, в условиях H

величина σ| будет несмещенной оценкой изменчивости от неучтенных причин,

т. е. для σ!. Аналогично eel + Tal

— оценка ожидаемого среднего квад-

рата взаимодействия среднего квадрата (табл. 19.7), которая приведена

в табл. 19.6 как 32 527,48. Тогда, разделив на г выражение σ| + гст

тр

— σ| =

SOO

Фиг. 19.7. Расхождения между данными по образ-

цам в зависимости от операторов.

гвтр, получаем оценку для σ„

_ 32 527,48—8 247,69

Omp — 7

24]279,79

6069,95.

Точно так же оценки ожидаемых средних квадратов для двух главных

эффектов будут

- MS

-MS

P =

~>тр

тг

33 744,96-32 527,48

:50,728

-MS

тор

рг

302 765,4— 32 527,48

:13 511,896.

Различия между средними по образцам явно больше, чем любые другие

изменения; изменчивость за счет ошибок стоит на втором месте по величине,

эффект от взаимодействия тоже может считаться большим. Различия между

данными исполнителей относительно малы.

334

ГЛАВА 1 г

По -видимому, для выработки подходящей рекомендации оптимального

распределения объектов в выборке требуется эксперимент, в котором взаи-

модействие контролировалось бы значительно лучше. При подходящем конт-

ролируемом эксперименте различия операторов должны быть независимы

от различий по образцам; и если взаимодействия нет, то во всем исследовании

ошибка (изменения от неучтенных причин) легко может быть уменьшена

повторными измерениями.

Таблица 19.9

Точечные оценки [385] ожидаемых средних квадратов

и стандартных отклонений

Источник

изменчивости

Оценка средних квадратов

Стандартное отклонение

Источник

изменчивости

Оценка средних квадратов

кодированное

декодированное

Операторы

Образцы

Взаимодействие

Ошибка

= 50,728

Om=

511,896

= 6 069,95

σ| = 8 247,69

CTp = 7,12

= 116,24

CTmp = 77,91

= 90,82

0,0007

0,0116

' 0,0078

0,0091

Можно было заметить, что дисперсия генерального среднего выражается

как

— σ|,

2 σ?„„ о?

Yar

)

= — + -

^ Ч—— H

' ρ т тр

трг

и что увеличение количества повторных замеров уменьшает только последний

член, в то время как число образцов содержится в знаменателе трех составля-

ющих дисперсии.

Именно поэтому совершенно необходимо стремиться к исследованию

большего количества образцов и в то же время — к уменьшению дисперсии

путем соответственной подготовки операторов. Различия между показаниями

различных исполнителей не должны беспокоить нас, если можно добиться

постоянства этих различий, т. е. если у

= 0.

19.9. ПРОЧИЕ АСПЕКТЫ ДВУХФАКТОРНОГО АНАЛИЗА

Несмотря на то что цель настоящего эксперимента — определение объем-

ной плотности песчаников формации Поконо — узко ограничена, этот экспе-

римент имеет значение для других исследований, аналогичных по структуре. '

Например, используя разобранный план, экспериментатор может вначале

предпринять пробное исследование, если есть намерение повторить экспери-

мент на этих же образцах и с этими же исполнителями, а затем уже проана-

лизировать всю совокупность. Разумеется, его обычно интересуют не дис-

персии, а среднее по всей совокупности. Так, если в выборке представлены

все элементы совокупности, сумма отклонений равна нулю. Если проана-

лизирована вся совокупность, проверка гипотез не требуется, так как в этом

случае результат выражается уже точными значениями параметров, а не

их статистическими характеристиками.

С одной стороны, эти шесть образцов могут представлять всю совокуп-

ность, но группа операторов представляет случайную выборку из бесконеч-

ной совокупности, с другой — одни и те же операторы используются неод-

нократно, а образцы представляют случайную выборку из совокупности бес-

конечного объема. Такая альтернативная постановка известна под названи-

ем смешанной модели [27].

ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

335

При практической работе может встретиться любая комбинация таких

ситуаций. Каждая из них, как и следует ожидать, накладывает свой отпе-

чаток на структуру эксперимента вследствие того, что прогноз, сделанный

на основании данного анализа, должен быть применим к различным физиче-

ским состояниям и различным совокупностям.

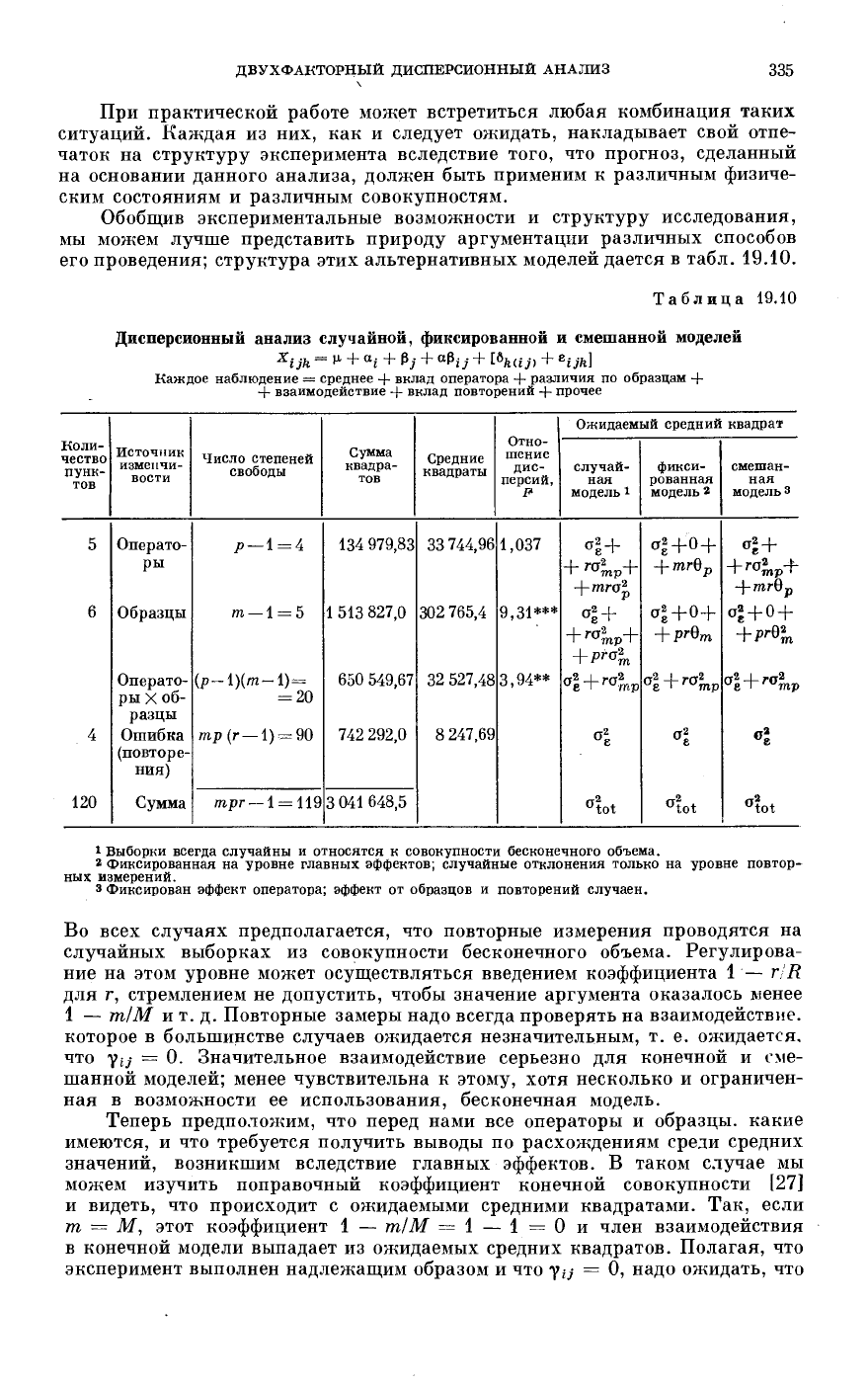
Обобщив экспериментальные возможности и структуру исследования,

мы можем лучше представить природу аргументации различных способов

его проведения; структура этих альтернативных моделей дается в табл. 19.10.

Таблица 19.10

Дисперсионный анализ случайной, фиксированной и смешанной моделей

ijk

= μ + а

+ β

· + αβ

ί;

· + I6

h(ij1

+ e

ijh

]

Каждое наблюдение = среднее + вклад оператора + различия по образцам +

+ взаимодействие + вклад повторений -f прочее

Отно-

шение

дис-

персий,

Ожидаемый средний квадрат

Коли-

чество

пунк-

тов

Источник

изменчи-

вости

Число степеней

свободы

Сумма

квадра-

тов

Средние

квадраты

Отно-

шение

дис-

персий,

случай-

ная

модель ι

фикси-

рованная

модель 2

смешан-

ная

модель з

Операто-

ры

р —1=4

134 979,83

33 744,96

1,037

I +

+ <р+

+ mra

σΙ+0 +

+ mrQ

Iip+

+ mrQ

Образцы

то —1 = 5

1 513 827,0

302 765,4

9,31***

mp+

+ P™m

σ|+0 +

+ prQm

σ? + 0 +

Операто-

ры χ об-

разцы

Ошибка

(повторе-

ния)

(р-1)(/п-1) =

= 20

тр (г —1) = 90

650 549,67

742 292,0

32 527,48

8 247,69

3,94**

°l +

°mp

°l + ™mp

«I

120 Сумма

трт —1 = 119

3 041 648,5

°tot

tot

®tot

ι Выборки всегда случайны и относятся к совокупности бесконечного объема.

2 Фиксированная на уровне главных эффектов; случайные отклонения только на уровне повтор-

ных измерений.

3 Фиксирован эффект оператора; эффект от образцов и повторений случаен.

Во всех случаях предполагается, что повторные измерения проводятся на

случайных выборках из совокупности бесконечного объема. Регулирова-

ние на этом уровне может осуществляться введением коэффициента 1 — г!R

для г, стремлением не допустить, чтобы значение аргумента оказалось менее

1 — т/М и т. д. Повторные замеры надо всегда проверять на взаимодействие,

которое в большинстве случаев ожидается незначительным, т. е. ожидается,

что y

j = 0. Значительное взаимодействие серьезно для конечной и сме-

шанной моделей; менее чувствительна к этому, хотя несколько и ограничен-

ная в возможности ее использования, бесконечная модель.

Теперь предположим, что перед нами все операторы и образцы, какие

имеются, и что требуется получить выводы по расхождениям среди средних

значений, возникшим вследствие главных эффектов. В таком случае мы

можем изучить поправочный коэффициент конечной совокупности [27]

и видеть, что происходит с ожидаемыми средними квадратами. Так, если

т = М, этот коэффициент 1 — т/М = 1 — 1 = 0 и член взаимодействия

в конечной модели выпадает из ожидаемых средних квадратов. Полагая, что

эксперимент выполнен надлежащим образом и что у и = 0, надо ожидать, что

336

ГЛАВА 1 г

критерий отношения дисперсий, проверяющий взаимодействие, окажется

незначительным, т. е.

(01+Г0тр)/0% <. F05, (р_1) (m-1), pm(r-i)·

Следовательно, подходящим остаточным членом для проверки главных эффек-

тов является σΐ; иногда ожидаемые значения средних квадратов для главных

эффектов записываются соответственно как σ\ + гтθ

и а\ + rpQ

, чтобы под-

черкнуть, что они не являются оценками изменчивости, как это мы имеем

в бесконечной модели.

JTenepb рассмотрим модель бесконечной совокупности, модель 2. Так как

т теперь ничтожно мало по сравнению с M ( и ρ по сравнению с P соответ-

ственно), коэффициент поправки конечной совокупности будет равным

I--S-=I-O=I

и аналогично

1—р/Р',

в таких условиях взаимодействие по-прежнему содей-

ствует дисперсии в ожидаемом среднем квадрате каждого главного эффекта.

Как ошибка Ъ\, так и взаимодействие могут быть использованы для проверки

главных эффектов, если будет доказано, что взаимодействие незначительно.

Иногда эти два оценочных фактора объединяют в качестве оценки одного

и того же источника изменчивости, если O

практически близко нулю (т. е.

незначительно или не более чем σΐ), а также для получения «более

лучшей»

оценки погрешности. Но так как оценка дисперсии взаимодействия относится

к выборочной ошибке, а «стабильная» оценка σ„

всегда имеется, ее значение

вследствие малого числа степеней свободы может пригодиться, но может

и не пригодиться.

С другой стороны, если взаимодействие значительно больше ошибки

_(_ Γθ„

)/σ1 значительно], оно становится основой для проверки глав-

ных эффектов. Следует указать на два момента. Если y

j Φ 0, рекомендации

будут не столь точными, как для случая, когда у

= 0. Как отмечал Шеффе

{385] и иллюстрировалось примерами в ранее описанных экспериментах,

если главный эффект значительно больше взаимодействия, нет необходимости

принимать во внимание, что каждое определение объемной плотности каждым

оператором всегда оказывается большим или меньшим относительно опреде-

ления объемной плотности по другому образцу.

Кроме того, когда в разбивке по двум признакам без повторных замеров

нет оценки взаимодействия, тогда подразумевается, что у у = O

; если такое

предположение не выполняется, оценка главных эффектов приводит к оши-

бочным заключениям.

Теперь предположим, что эти же операторы работают снова, но они уже

обрабатывают новые образцы, отобранные случайным способом из совокуп-

ности бесконечного объема. Тогда 1 — р/Р = 0, а 1 — mlM = 1; при таких

обстоятельствах взаимодействие не играет роли главного эффекта в разли-

чиях между средними по образцам, но оно может оказать существенное влия-

ние на различия между средними по исполнителям. Подходящий остаточный

член для проверки средних квадратов по образцам — это σ|, поскольку под-

ходящей «ошибкой» для проверки расхождений в определениях операторов

является взаимодействие. Значительное взаимодействие вновь ставит в тупик

экспериментатора и затрудняет вывод общего заключения.

Подобные планы могут быть изменены, если число операторов рассма-

тривать как взятое из конечной совокупности операторов, когда р/Р суще-

Если взаимодействие имеется, оно увеличивает оценку ошибки.

ОДНОФАКТОРНЫЙ

ДИСПЕРСИОННЫЙ АНАЛИЗ

337

ственно больше нуля, но не равно единице. Тогда коэффициент, увеличиваю-

щий оценку дисперсии за счет взаимодействия, дробен; и если только эффект

от взаимодействия не равен нулю, проверку главных эффектов не стоит

и начинать [27].

19.10. ПРЕДПОЛОЖЕНИЯ, ВХОДЯЩИЕ В РАЗЛИЧНЫЕ ПЛАНЫ

ЭКСПЕРИМЕНТОВ ПРИ ДВУХФАКТОРНОМ АНАЛИЗЕ

Из вышесказанного должно быть ясно, что различные формы дисперсион-

ного анализа опираются на различные предположения, несмотря на то что

вычислительная процедура и таблица общей формы дисперсионного анализа

идентичны. Поэтому желательно четко сформулировать те из предположений,

которые включаются в каждый конкретный эксперимент в качестве состав-

ной части его структуры. Эти предложения подробно рассматривали Эйзен-

харт [109], Беннетт и Франклин [27] и Шеффе [385]. Случаи несостоятельно-

сти этих предположений описаны также Кокраном [75] и в вышеприведенных

руководствах.

Данная модель в общем виде записывается как

Xijk = μ + «ι + β; + Уи + £цц).

Прежде всего рассмотрим двухфакторное расположение наблюдений

(одно наблюдение на клетку) строками и столбцами [109]. Если «дисперсион-

ный анализ» выполнен и его результаты суммированы в таблице анализа,

которая и представляет собой обобщение этих данных, взаимоотношения

между суммами квадратов и т. п. являются алгебраическими свойствами

такого упорядочения, то никаких предположений не требуется. Когда же

данные рассматриваются в качестве выборки из некоторой совокупности

и требуется доказать, что заключения, основанные на данных анализа, долж-

ны быть распространены на всю совокупность, из которой сделана выборка,

это уже статистическое заключение, и, чтобы оно приобрело ценность аргу-

мента, должны выполняться некоторые вводимые предположения. На этой

стадии необходимо точно определить, какого рода заключения мы собираемся

выводить и, следовательно, определить род модели, представляющей экспе-

римент. Вначале допустим, что экспериментальная ситуация представлена

фиксированной моделью Первое предположение заключается в том, что

наблюдения представлены значениями случайных величин, имеющих фик-

сированные истинные средние значения.

Из этого предположения следует, что наблюдения X

, будучи упоря-

доченными по двум признакам, распределены с истинными средними значе-

ниями mij и что E (Xtj) = rriij, или 2 (Хц —

и) = 0.

Второе предположение касается дополнительных эффектов действия

факторов в эксперименте. Следовательно, если гипотетические истинные сред-

ние mij Д

я каждой клетки могут быть записаны как

U =

(α«

+ α.) +

(β> —

β·),

где μ — фиксированная постоянная, истинное среднее α будет истинным сред-

ним ί-го ряда (среднее ί-го воздействия), а β — истинное среднее /-го столбца

или

j-το

воздействия по столбцам, то наблюдения позволят оценить различия

между средними любого определенного действия данных условий. Исходя

из разбивки по двум признакам — по операторам и образцам.— различия

между средними по образцам, скажем

а.

оцениваются различием между

средними первого и второго рядов разбивки. Эти полученные различия явля-

ются несмещенной оценкой ИСТИННОГО различия в значениях объемной плот-

ности, которое существует между образцами 1 и 2.

Такая модель у Эйзенхарта [109] называется моделью первого типа.

22—429

338

ГЛАВА 1 г

Снова в этом случае изменчивость между средними по образцам не влияет

на различия средних по операторам, т. е. взаимодействие равно нулю (yij = 0).

Когда аддитивность не выполняется, различие между

и а

приложимо·

только к определенному оператору.

Согласно третьему предположению, случайные величины X

имеют

общую дисперсию σ

и все ковариации равны нулю; это предположение обес-

печивает аддитивность дисперсий и действенность использования дисперсий

ошибки, усредненных по всему эксперименту.

Для полного завершения анализа и использования критерия для про-

верки гипотезы требуется еще одно, четвертое допущение: все Хц распреде-

лены нормально. Ослабление любого из этих допущений приводит к неточным

заключениям, которые основаны на сравнении средних и сопровождающих

их критериев. Чтобы понять, что именно относится к таким ослабленным тре-

бованиям, каждый такой случай необходимо внимательно рассмотреть

в отдельности.

19.11. РАЗЛИЧИЯ МЕЖДУ СРЕДНИМИ

Довольно часто экспериментатор хочет продвинуться дальше демонст-

рирования различий между средними по той или иной классификации. Тогда

надо сравнить эти средние и расположить их в некотором порядке; сущест-

вует множество различных альтернатив и, в частности, процедур, когда срав-

нение превращается в эксперимент (сравните с разделом 18.8). Возможно раз-

делить наиболее различающиеся средние попарно с числом степеней свободы 1

для каждого сравнения [44], что может представлять определенный интерес.

Требование ортогональности может быть выполнено по нескольким срав-

нениям.

В общем для сравнений или сопоставлений средних значений, заданных

до эксперимента, ошибка определяется разностью между двумя средними

и характеризуется величиной 2σ|, где а\ — соответствующая дисперсия

ошибок.

С другой стороны, когда сравнения выполняют после изучения резуль-

татов эксперимента, целесообразно применить доверительные интервалы

Шеффе или Тюки, которые зависят от числа величин при подсчете каждого

среднего и соответственно равны или не равны [385]. Необходимо в каждом

случае проводить различия между конечной (модель 1), бесконечной (модель 2)

и смешанной моделями, в связи с чем критерий для проверки гипотезы

становится весьма сложным

[44]. Методы упорядочения средних описаяы

также Беннеттом и Франклином [27], Бечофером [23], Бечофером, Даннет-

том и Собелом [24].

19.12. ПРИМЕРЫ ДВУХФАКТОРНОЙ КЛАССИФИКАЦИИ

Множество примеров применения дисперсионного анализа с классифи-

кацией по двум признакам для решения геологических вопросов дано Мил-

лером и Каном [299], Крамбейном и Миллером [257], а также Гриффитсом

и Розенфельдом [161]. Гриффите и Розенфельд [156] детально разобрали клас-

сификацию по двум признакам с повторениями в приложении к измерениям

формы кварцевых зерен в осадках.

Очевидно, этот способ является эффективным инструментом в широком

диапазоне экспериментальных ситуаций, которые возникают при исследова-

нии геологических проблем. Следовательно, необходимо подчеркнуть, что

преимущества и недостатки этого приема выявляются в процессе его конкрет-

ных приложений.

Заметим, что арифметические действия здесь довольно просты; сложно лишь

обоснование соответствующих выводов.

ОДНОФАКТОРНЫЙ

ДИСПЕРСИОННЫЙ АНАЛИЗ

339

Во-первых, надо предварительно определить, что в данной ситуации

более эффективно — стратификация или блокирование популяции. Необхо-

димо отметить, что связанные со стратификацией степени свободы, которые

теряются из-за «ошибки», все же представляют существенную часть диспер-

сии. Если стратификация проведена и слоев нет, это основание классифика-

ции уменьшает число степеней свободы для «ошибки», но вместе с этим умень-

шает и чувствительность эксперимента.

Во-вторых, очень важно решить, какая из моделей рассматривается

(фиксированная, случайная или смешанная); только так по эксперименталь-

ным результатам могут быть сделаны правильные выводы.

В-третьих, эксперимент следует контролировать в такой степени, чтобы

член взаимодействия действительно равнялся нулю; при наличии каких-

либо сомнений для проверки такого предположения рекомендуется приме-

нить повторные замеры. Довольно часто доказанное наличие взаимодействия

дает возможность перепланировать будущие эксперименты с целью свести

к нулю или по крайней мере уменьшить его эффект.

Наконец, использование неодинаковых количеств повторных замеров

в данных классах можно легко приспособить к плану эксперимента. Это,

однако, не надо понимать как оправдание использования разных количеств

повторений, ибо последние усложняют как оценки дисперсии, так и срав-

нение средних, что при значительной дисперсии взаимодействия может испор-

тить весь анализ.

Прочие

ГЛАВА 19

экспериментальные решения

Если в результате взаимодействия многочисленных факторов возникла

путаница и затруднения, то еще до освоения данных фактов может потре-

боваться продолжение изучения этих результатов и дальнейшее экспе-

риментирование. Трудности вызываются не тем, что неудачен экспери-

мент, а тем, что сложны сами явления.

W. G. Cochran, G. Μ. Сох, Experimental Designs, John

Wiley and Sons, Inc., 2nd ed., p. 153, 1957

20.1. ВВЕДЕНИЕ

По мере того как экспериментатор все более знакомится с возможностя-

ми экспериментального решения, обнаруживается, что существует весьма

широкий круг задач, в которых дисперсионный анализ играет основную роль.

Затем следует рассмотрение классификации по трем признакам, по четырем

и далее, до классификаций более высокого уровня. Однако по мере возраста-

ния сложности классификации количество наблюдений возрастает гораздо

быстрее, так что экспериментатор, хорошо понимающий, к чему это может

привести, бывает вынужден игнорировать некоторые причины изменчивости

и использовать сбалансированный неполный блок и несбалансированный

блок с целью уменьшить количество требуемых наблюдений. Примеры сба-

лансированного неполного блока и несбалансированного блока будут при-

ведены ниже.

Уже упоминалось, что если классификация основана на порядковой шка-

ле или шкале более высокого уровня, можно применить факторный анализ;

однако в геологической литературе пока есть лишь незначительное количе-

ство таких решений. Аналогично, если это потребуется, можно объединить

дисперсионный анализ с регрессионным, а также применить ковариационный

анализ (примеры см. у Миллера и Кана [299]). На этой стадии рекомендуем

пользоваться справочниками по экспериментальным решениям, в которых

можно выбрать подходящий способ отбора, соответствующий требованиям

плана; прекрасные руководства по этому вопросу даны Кокраном и Коксом

[79], Беннеттом и Франклином [27], Браунли [44] и Кемпторном [232]. Фак-

торные эксперименты хорошо представлены в промышленной сфере [91], но все

это никоим образом не исчерпывает литературу по экспериментальным

решениям. При выборе решения следует также ясно понимать, что в некото-

рых более сложных случаях ощутимой проблемой становятся арифметиче-

ские вычисления; тогда выгодно применять электронно-вычислительные

машины. Кроме того, необходимо помнпть, что следует сначала найти исход-

ные данные, а уже потом начинать их собирать. В общем, чем проще план

обработки, тем легче извлечь всю информацию, которая заключена в исход-

ных данных, Η если экспериментатор знает, что он делает, он всегда сможет

свести свою проблему к простому решению.

ПРОЧИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕШЕНИЯ

341·

20.2. ТРЕХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

Геолог интуитивно прибегает к классификации по трем признакам, так

как ему известны три основания для классификации — одно стратиграфиче-

ское и два географических измерения, составляющие типовую решетку гео-

логического пространства. Готовясь использовать классификацию по трем

признакам, исследователь должен точно определить интересующую его гене-

ральную совокупность и свою цель: или сравнение средних (фиксированная

модель — модель 1), или сравнение дисперсий (случайная модель — модель

2), или же то и другое (смешанная модель — модель 3). Этих двух характе-

ристик достаточно для выбора надлежащего плана наблюдений. Если за дан-

ный массив пород берутся впервые, желательно включить в план повторные

измерения в качестве средства проверки взаимодействия второго порядка;

если же этот объект уже исследовался и известно, что взаимодействия отсут-

ствуют или они незначительны, можно применить более эффективное реше-

ние, такое, например, как латинский квадрат (см. раздел 20.4).

Предположим, что вопрос касается опробования каменной осыпи и что

случайной величиной являются длинные оси (а) кварцитовых валунов из

из этой осыпи. Чтобы сократить число измерений, приходящихся на опера-

тора, и свести дело к простой задаче, надо много операторов. Основная цель —

изучить изменчивость длинных осей кварцитовых галек; следовательно, под-

ходящей моделью представляется бесконечная совокупность. С другой сто-

роны, чтобы установить, имеется ли тенденция изменения размеров, требу-

ется изучить также различия между средними значениями осей и ряды сред-

них значений, пересекающие осыпь. Способ отбора заключается в подразде-

лении осыпи на небольшие площади и в отборе образцов с этих площадей.

Чтобы можно было применить модель бесконечной совокупности (так как

протяженность осыпи не бесконечна), требуется использовать выборку с

с возвращением, при которой осыпь подразделяется на ряды и колонки. Рас-

стояния между рядами и колонками должны быть случайными, но в каком

из этих отрезков должна уложиться длина наибольшего валуна целое число

раз, надо установить в начале исследования. Отбор проб с возвращением

позволяет переопробование некоторых рядов и (или) колонок, если площадь

отбора в достаточной мере соизмерима с площадью осыпи.

Каждый из ρ операторов измеряет q валунов в каждом пересечении сети,

составленной из рядов и колонок; учитывая предыдущий опыт, по каждой

стороне надо замерить по крайней мере 8 валунов, так что pq > 8. Практи-

чески оператор в круге радиуса 6 футов проводит наудачу диаметр и замеряет

валуны на его концах. Такие диаметры должны быть так расположены сим-

метрично с углом θ° между смежной парой, чтобы было обеспечено pq > 8.

Такой способ отбора приводит к классификации по трем признакам,

ибо главных эффектов три: операторы, ряды, колонки. Здесь мы имеем три

смешанных эффекта первого порядка, а именно: операторы X ряды, операто-

ры X колонки, ряды X колонки; затем один смещанный эффект второго

порядка: операторы X ряды X колонки. Так как каждый оператор замерит q

валунов в каждом пересечении ряд X колонка, то в каждом классе оператор

X ряд X колонка будет q повторных замеров. Такой способ значительно

сложнее классификации по двум признакам; классификация же по четырем

признакам или более высокого порядка еще сложнее, например, при четы-

рехфакторном анализе: четыре главных эффекта, шесть смешанных эффектов

первого порядка, четыре смешанных эффекта второго порядка π один— третье-

го; такой способ может понадобиться при анализе причин изменчивости свойств

размеров длинных осей кварцевых зерен по шлифам (гл. 3). Пять основных

свойств (гл. 3) потребуют уже пятифакторной классификации с разбивкой,

которая иллюстрируется табл. 20.1.