Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

362 ГЛАВА 1 г

Тогда

R-J

P = ^

(21.12)

-JSx

(21ЛЗ)

или

У —F=P(X-X), (21.14)

что дает

У = У+р(Х-Х);

после замещения численных значений У и X

Υ = α+ βΧ. (21.15)

Дисперсия регрессионных значений У дается выражением

σγ.Α = ,

где Y

—

наблюдаемое значение У, a Y

—

вычисленное значение У (оценка

для μ^.χ) для данного значения Xj. Оценкой будет величина

У OV-^c)

<ήτ.χ=

, (21.16)

где две степени свободы теряются при оценках α и β по наблюдениям.

Величина (η

—

2) ay .χ/ο

с χ

распределена как с числом степеней свободы

η —

2 [27,44,454]. Формула, наиболее удобная для нахождения этой дис-

персии, определяется следующим образом. Так как

Σ (Yi- Yc)

to* =

2 (F

__ ά _ рх

г)

- CC - рх,) =

= Σ Yi (Yi - ά- to - ά Σ (Yt - ά·-

βΧΟ

Σ (Yi - ά •- ρχ,),

а при нахождении линии наилучшего приближения величина 2 (Yi-&

—

βΧ;)

приравнивается нулю и два последних члена обращаются в нуль, следова-

тельно,

= Σ ^tYt

у,

У?

—ά У, У; —β Vx

= ^

^ · (21.17)

21.6. ЗАВИСИМОСТЬ МЕЖДУ СОДЕРЖАНИЕМ КАРБОНАТОВ

И ПОРИСТОСТЬЮ В ПЕСЧАНИКАХ КАУ-РАН

Пористость нефтеносных песков, измеряемая в процентах, часто сильно

зависит от количества карбонатного цемента в песках; в нефтеносных пенсиль-

ванских песчаниках Кау-Ран (Западная Виргиния) [167] для некоторого

интервала значений пористости установлена линейная форма такой зави-

симости. Там, где содержание карбоната менее 5%, связи между карбонат-

ностью и пористостью не наблюдается [167]; то же можно сказать и о тех

случаях, когда карбонат представлен обломками раковин. Максимальная

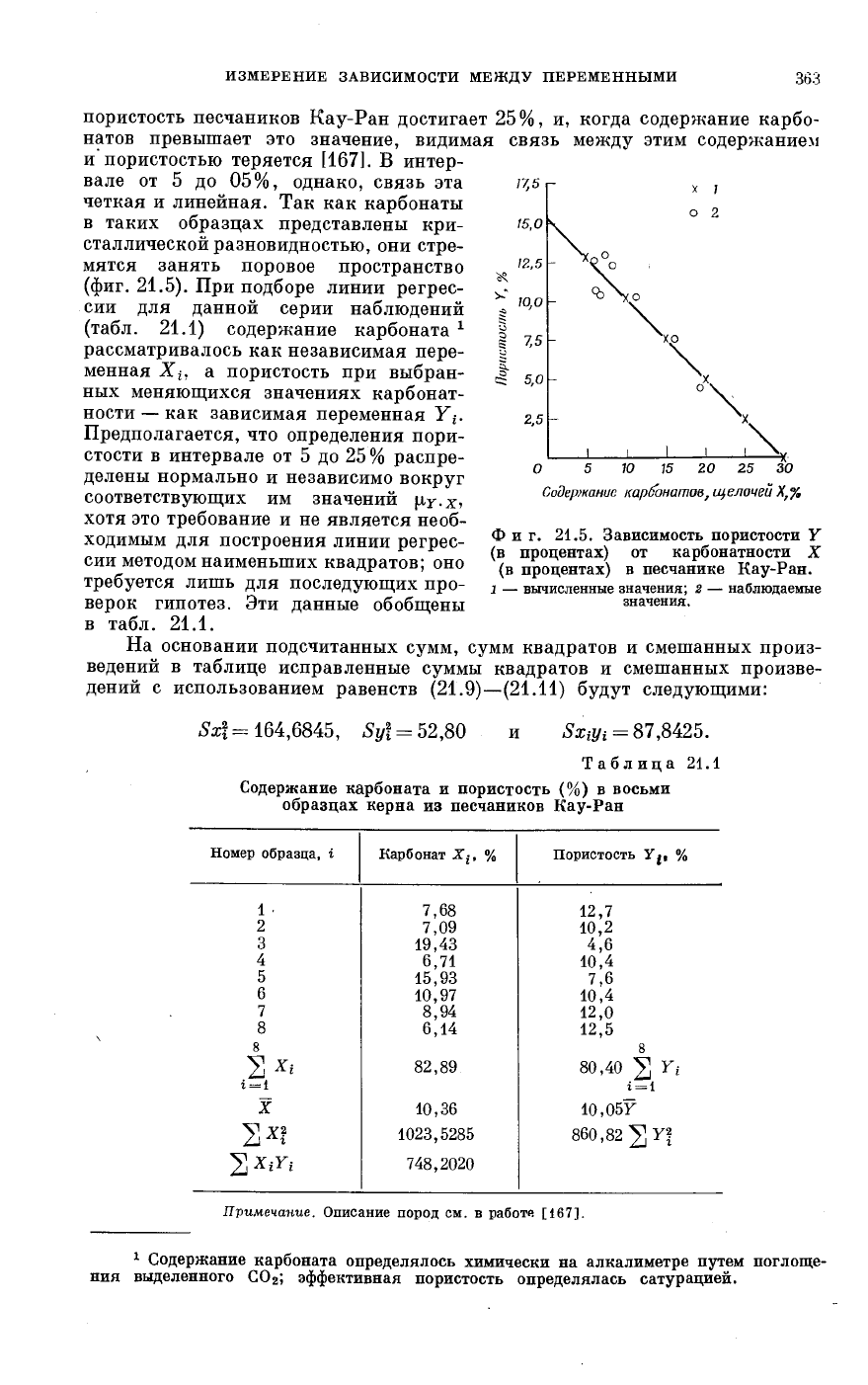
ИЗМЕРЕНИЕ ЗАВИСИМОСТИ МЕЖДУ ПЕРЕМЕННЫМИ

363

/7 5

15,0

12,5

70,0

S 7,5

с:

пористость песчаников Кау-Ран достигает 25%, и, когда содержание карбо-

натов превышает это значение, видимая связь между этим содержанием

и пористостью теряется [167]. В интер-

вале от 5 до 05%, однако, связь эта

четкая и линейная. Так как карбонаты

в таких образцах представлены кри-

сталлической разновидностью, они стре-

мятся занять поровое пространство

(фиг. 21.5). При подборе линии регрес-

сии для данной серии наблюдений

(табл. 21.1) содержание карбоната

рассматривалось как независимая пере-

менная X

, а пористость при выбран-

ных меняющихся значениях карбонат-

ности

—

как зависимая переменная Y

Предполагается, что определения пори-

стости в интервале от 5 до 25% распре-

делены нормально и независимо вокруг

соответствующих им значений μγ\χ,

хотя это требование и не является необ-

ходимым для построения линии регрес-

сии методом наименьших квадратов; оно

требуется лишь для последующих про-

верок гипотез. Эти данные обобщены

в табл. 21.1.

На основании подсчитанных сумм, сумм квадратов и смешанных произ-

ведений в таблице исправленные суммы квадратов и смешанных произве-

дений с использованием равенств (21.9)-(21.11) будут следующими:

5,0

2,5

5 10 15 20 25 30

Содержание карбонатов, щелочей Х,%

Фиг. 21.5. Зависимость пористости Y

(в процентах) от карбонатности X

(в процентах) в песчанике Кау-Ран.

1 — вычисленные значения; 2 — наблюдаемые

значения.

Sxl= 164,6845, Syl = 52,80 и Sx

iyi

= 87,8425.

Таблица 21.1

Содержание карбоната и пористость (%) в восьми

образцах керна из песчаников Кау-Ран

Номер образца, i

Карбонат X

, %

Пористость Y

, %

1 •

7,68

12,7

7,09 10,2

19,43 4,6

6,71

10,4

15,93

7,6

10,97

10,4

8,94

12,0

6,14

12,5

82,89

80,40 2 Y

г = 1

i = l

10,36 10.05Г

Σ*!

1023,5285

860,82 2

748,2020

Примечание. Описание пород см. в работе [167].

Содержание карбоната определялось химически на алкалиметре путем поглоще-

ния выделенного CO

; эффективная пористость определялась сатурацией.

364 ГЛАВА 1 г

Отсюда

R-'.

Sx\ ~~ 164,6845

о Sxjy

—84,8425 η MW

164 R84S - —U

OlDZ.

. ^ 2

<~Р Σ

i_ 80,4 + 0,5152 x 82,89 ggg

η 8 '

Уравнение регресии

Y = 15,388

—

0,515Х.

Эта линия построена на фиг. 21.5. Она показывает, что на каждую полу-

единицу уменьшения карбонатности пористость возрастает на единицу.

Дисперсия Y

по отношению к линии регрессии следует из равенства

(21.17):

860,82—15,388 x 80,40 + 0,515 x 748,202 .

Ογ.χ = 0 = Ι,ΟΙΟ,

ИЛИ

= 1,231.

21.7. ПРОВЕРКА ГИПОТЕЗЫ РАВЕНСТВА КОЭФФИЦИЕНТА РЕГРЕССИИ

И ВЕЛИЧИНЫ СДВИГА (d) НУЛЮ

Из полученного значения σγ.χ = 1,231 находят величину дисперсии

выборочного коэффициента регрессии (β):

3Γ

(β) = σ|=^ (21.18)

1,515 ^

0i00920

164,6845

Теперь можно проверить, отражает ли оценка β тот факт, что истинное

значение

= 0. Используем статистику

β_β

(21.19)

/Var (β)

. -0,515-0 ,о

7П

- 0,0959 -

В условиях нулевой гипотезы β = 0 статистика t распределена как t-

критерий Стьюдента с числом степеней свободы ν = η — 2.' Следовательно,

при уровне значимости 0,01 (P

) для ν = η — 2 = 6, критическое значение

равно 3,71, но так как вычисленное нами значение превышает 3,71, нулевая

гипотеза (β = 0) отвергается и приходится согласиться, что β = —0,515

не характеризует совокупность, в которой β = 0; доверительные пределы

для β при 99-процентной надежности будут:

β-ίοι,

< β <

ί(Η,7ΐ-2<*β>

(21-20)

или

- 0,515—3,71 χ 0,0959 <

<—0,515 + 3,71 χ 0,0959, —0,870 < β <—0,159.

Этот интервал не содержит нуля, т. е. коэффициент регрессии β значимо

отличается от нуля.

Аналогично дисперсия оценки α для ос равна

8Γ

(ά) = 4^1, (21.21)

ИЗМЕРЕНИЕ ЗАВИСИМОСТИ МЕЖДУ ПЕРЕМЕННЫМИ

365

т. е. для приведенного примера в цифрах

Var (а) = iiijpl = 0,2525

σά = 0,5025.

Доверительные пределы могут быть подсчитаны для α

α —ί

<α<ά+ί

,η-

σ- (21.22)

или для надежности P = 0,99 при ίοι,

β —

3,71

15,399 - 3,71 χ 0,503 < а < 15,388 + 3,71 χ 0,503;

13,552 <α< 17,254.

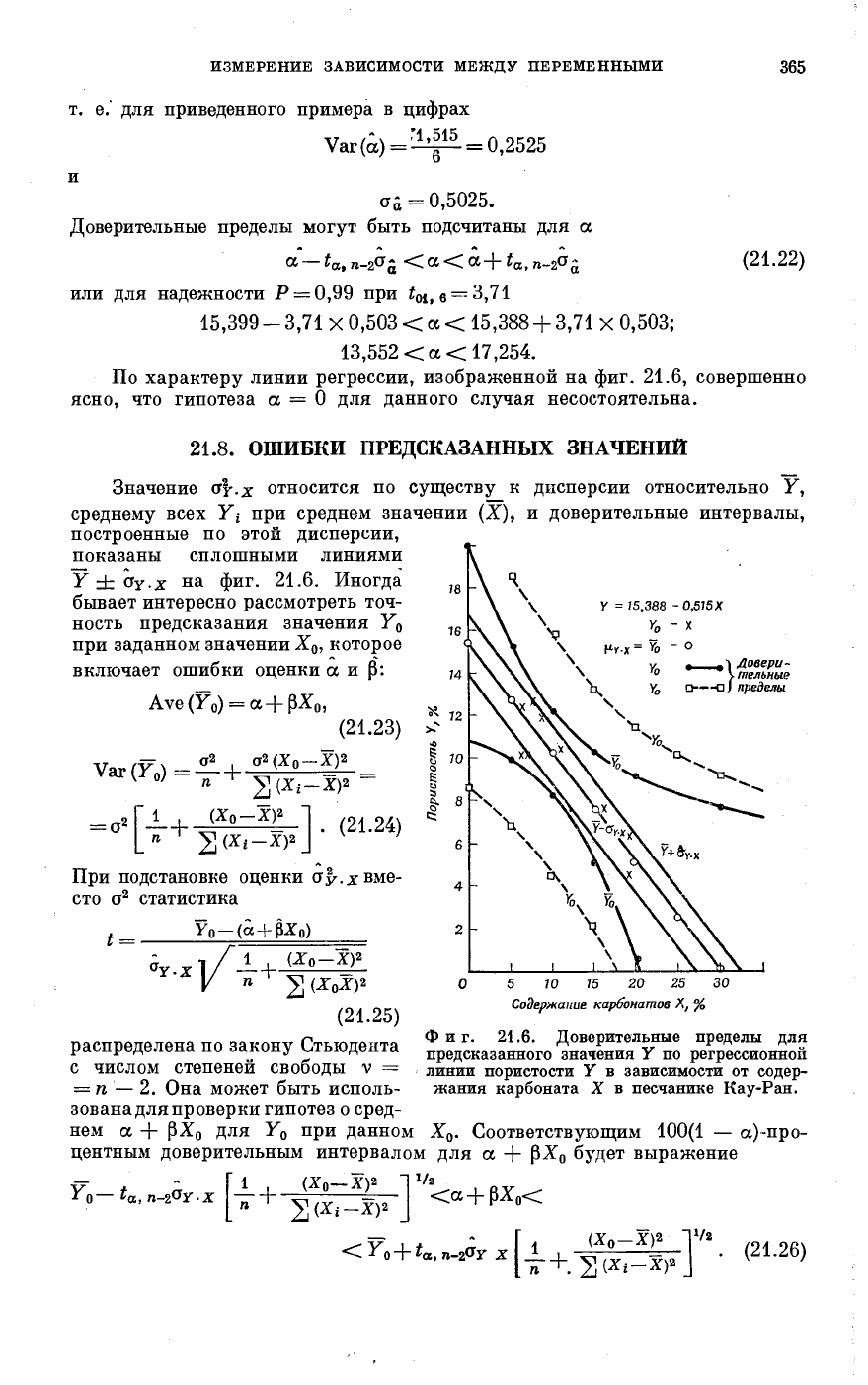
По характеру линии регрессии, изображенной на фиг. 21.6, совершенно

ясно, что гипотеза а = 0 для данного случая несостоятельна.

21.8. ОШИБКИ ПРЕДСКАЗАННЫХ ЗНАЧЕНИЙ

Значение β\.χ относится по существу к дисперсии относительно У,

среднему всех Y

при среднем значении (X), и доверительные интервалы,

построенные по этой дисперсии,

показаны сплошными линиями

У ± Ογ.χ на фиг. 21.6. Иногда

бывает интересно рассмотреть точ-

ность предсказания значения Y

при заданном значении X

, которое

включает ошибки оценки α и β:

0,5)5 X

Ave (Y

) = α + βΧ

}

Довери-

тельные

пределы.

Var (Y

)

TTs σ

(21.23)

-Ζ)2

= O

-X)

Σ (Xi-X)

-Χ)2

. (21.24)

При подстановке оценки σу.χ вме-

сто σ

статистика

t =

-(α + βΧ

)

Y-X

(Xo-X)

Σ (

οΧ)

(21.25)

распределена по закону Стьюдента

5 10 15 20 25 30

Содержание карбонатов λ, %

Фиг. 21.6. Доверительные пределы для

предсказанного значения Y по регрессионной

линии пористости Y в зависимости от содер-

жания карбоната X в песчанике Кау-Ран.

с числом степеней свободы ν =

= η— 2. Она может быть исполь-

зована для проверки гипотез о сред-

нем α + βΧ

для Y

при данном X

. Соответствующим 100(1 — (^-про-

центным доверительным интервалом для α + βΖ

будет выражение

— tlx, η-2

Υ·Χ

-X)

1/2

<α + βΧ

2 (Хг-X)

< Y

+ t

п-2<Уу

•+

(Xo-

-X)Z T

г-X)

(21.26)

366

ГЛАВА 21

Доверительные пределы по обе стороны линии регрессии, обозначенные

на фиг. 21.6 через Y

, являются примером этих границ, и можно заметить,

что прогноз значительно не соответствует области средних значений YHX.

С другой стороны, может оказаться, что надо будет определить довери-

тельные пределы для новых значений Y

при избранных X

, для которых

дисперсия Ογ.χ отдельных наблюдений должна быть прибавлена к следую-

щему выражению:

Var (Y

) - σ

' η

-X)

-X)*

тогда доверительный интервал будет следующим:

1 . (X

-*)

Υΰ±ί

,η-·ίΟΥ·Χ

2 (X

-X)*

1/2

(21.27)

(21.28)

Доверительные интервалы, обозначенные как Y

, показаны на фиг. 21.6.

Единичные наблюдения не предсказываются с достаточной степенью точ-

ности; она достигается лишь в том случае, когда количество их становится

довольно большим. Кроме того, точность не соответствует данным средним Y

при X. Становится ясным, что использование

Gy.

χ в качестве оценки погреш-

ности может привести к существенным ошибкам, если интересующие нас

измерения отражают отдельные наблюдения Y

21.9. ОЦЕНКА ПОГРЕШНОСТИ ДЛЯ «ПРЕДСКАЗАННОГО^!»

Довольно часто исследователь с целью установить взаимоотношение

между некоторым свойством эталонного объекта и его поведением при экспе-

рименте использует набор стандартов, определенных с очень малой погреш-

ностью; например, интенсивность линии на спектральной пластинке для

оценки количества элемента в веществе, интенсивность пика на рентгено-

грамме для определения количества минерала в смеси или же весовое коли-

чество углекислого газа, выделившегося при нагреве карбонатсодержащего

образца для оценки количества карбоната. Целью здесь является установ-

ление стандартной кривой, и при этом должны быть выполнены требования

регрессионной модели. Однако вслед за этим у экспериментатора появляется

желание перенести процедуру такой оценки с измерения эталона на новый

материал; предсказать, пользуясь полученной эталонной кривой, содер-

жание некоторого элемента или минерала в образце — это пример обращен-

ной оценки, в которой по наблюдаемому значению Y должно быть пред-

сказано значение X. Естественно, что исследователь хочет установить дове-

рительные пределы для этого «предсказанного X». Так как X было выбрано

с самого начала, оно представляет собой случайную переменную в вероят-

ностном значении, и так как X не обладает распределением погрешности,

ее невозможно оценить непосредственно; существует множество альтерна-

тивных возможностей оценки; этот вопрос в статистической литературе

является дискуссионным [3, 44, 454]. Исследователь должен быть знаком

со всеми способами, ибо каждая модель приспособлена к определенной

ситуации [3]. В данном случае, следуя Вильямсу [454] и Браун ли [44], задачу

можно представить как

= X + -Iip^, (21.29)

где X

— предсказанное значение X, соответствующее новому набору Yj

(;'

= 1, . . ., п), дающему Υ'

, а уравнение линии регрессии, основанной на η

парах Yjj, есть X

— Υ

=α + βΧ

. При данных ожидаемых значениях

ИЗМЕРЕНИЕ ЗАВИСИМОСТИ МЕЖДУ ПЕРЕМЕННЫМИ

367

= μγ.χ, истинное значение X по регрессии будет ε, а

Y-X-

ε = Χ-

(21.30)

что можно написать в виде

μγ.χ

—

β(ε

—

X) = 0.

Тогда дисперсия

Υ'

—

— β

(ε

—

Ζ) примет вид [3]

-P

= P {h<t<h), (21.31)

где P

, P

— вероятностные пределы, a J

, t

— соответствующие значения

ί-критерия Стьюдента; интервал по ε дает квадратичное выражение по ε

как для верхней, так и для нижней границ. Это может быть решено для

значений ε, скажем C

и ε

, путем применения таких выражений, как

t'Ja

„Г - / л α ν ,ν· I

/»

= Χ-

Р(у;-а)

Y-X

β2—р2

—P

(β

(У0-«)

2 (

i — X)

2°У

. X

- „ .. . (21.32)

Аналогичное выражение для C

содержит ί

вместо t

. Дисперсия для коэф-

фициента регрессии β входит в данное выражение в форме

}

•

2 (Xi-X)

/=1, 2.

(21.33)

Если это выражение приближается к нулю, реальных доверительных пре-

делов не существует. Отношение между β

и правым членом в выраже-

нии (21.33) представляется критическим, поэтому определяем

ή°

γ-χ

Если О-

> 2 (Xi-X)

можем использовать и такие выражения:

62 X'

Y'o — a hv

η J

(Yo- α)

2 (Xi-X)

1/2

(21.34)

(21.35)

X-

Ya-

Y-X Г/J_4_ M

I β I I V

2 (X

-X)

1/2

как приблизительные пределы для ε, если g < 0,1 [44]. Заметим, что если мы

располагаем только одним наблюдением нового значения Y

, то т = 1 и ра-

венство уменьшится до 1 +

In вместо

Im +

In.

В данном примере предполагается, что произведено определение пори-

CTOCi

H нового образца из некоторой совокупности. Каково содержание

карбоната и доверительных пределов для него? Новое значение Y

рав-

но 11,0% (пористость). Подставляя его в уравнение регрессии Y =

= 15,388—0,515Х, получаем значение карбонатности, равное 8,52%. Необ-

ходимые цифры для вычисления доверительных пределов следующие:

X = 10,36; Г= 10,05; ο

.χ = 1,231; 5®·= 164,6845;.

т = 1; п =

У; = 11,0.

368

ГЛАВА 1 г

Теперь можем вычислить величину критерия g при ί = 2,447 и числе сте-

пеней свободы б и P

Z-^ у. χ _ 2,447

χ 1,231

_ 9,073692 _ „ „„„

~ faSxl ~ (-0,515)

X 164,6845 ~ 43,678447

Итак, мы убедились в неадекватности аппроксимации, однако в целях иллю-

страции продолжаем вычисление:

10,36+ (11/)-¾) - (2,447-i|fi)

« 10,36+ (и,0

X ~

15,4

'ι ι

(4,3882)

1 +

( —

0,515)

Х 164,6845

-)х

1+4-4

(4,3882)

(—0,515) )

х/ .

следовательно, при надежности 0,95 интервал карбонатности будет нахо-

диться в пределах от 11,563 до 26,197%, а доверительные пределы, вычис-

ленные по полным равенствам,— от 12,599 до 29,629. Разумеется, оба эти

интервала совершенно нереальны, ибо критерий g находится вне диапазона

адекватных оценок. Вместо того чтобы уменьшать величину g, надо макси-

мально увеличивать количество наблюдений и их диапазон, так как тем

самым будут уменьшаться значения t и, возможно, Оу.х и увеличиваться

величина Sx

21.10. ПРОВЕРКА ГИПОТЕЗЫ ОТСУТСТВИЯ РЕГРЕССИИ

С ПОМОЩЬЮ ДИСПЕРСИОННОГО АНАЛИЗА

Когда уравнение регрессии представлено через оценки

Ύ, = ά + ρΧ, + βι,

оно сходно со структурным уравнением (18.4), описанным на основе дис-

персионного анализа, и в этом случае можно проверить гипотезу равенства

нулю коэффициента регрессии с помощью дисперсионного анализа. Полная

дисперсия наблюдений У выражена как

2 (Y

-Tf,

г=1

что можно записать

2 (Го-F)

= 2 (Y

-у

)

+2 (Y

-F)

, (21.36)

1=1 .1 , 1

откуда ясно, что эта дисперсия по отношению к среднему составляет откло-

нения наблюдаемого значения от значения регрессии Y

плюс отклонения

регрессии от среднего; смешанные произведения, как обычно, равны нулю.

Если мы рассматриваем взаимоотношения, исходя из отклонений от сред-

него, т. е.

и ι/;, то ос= 0 и процедура анализа может быть сведена в табл. 21.2.

Процедура вычисления включает нахождение полной суммы квадра-

тов Syl и суммы квадратов, обусловленной регрессией остаток находят

путем вычисления разности.

ИЗМЕРЕНИЕ ЗАВИСИМОСТИ МЕЖДУ ПЕРЕМЕННЫМИ 369

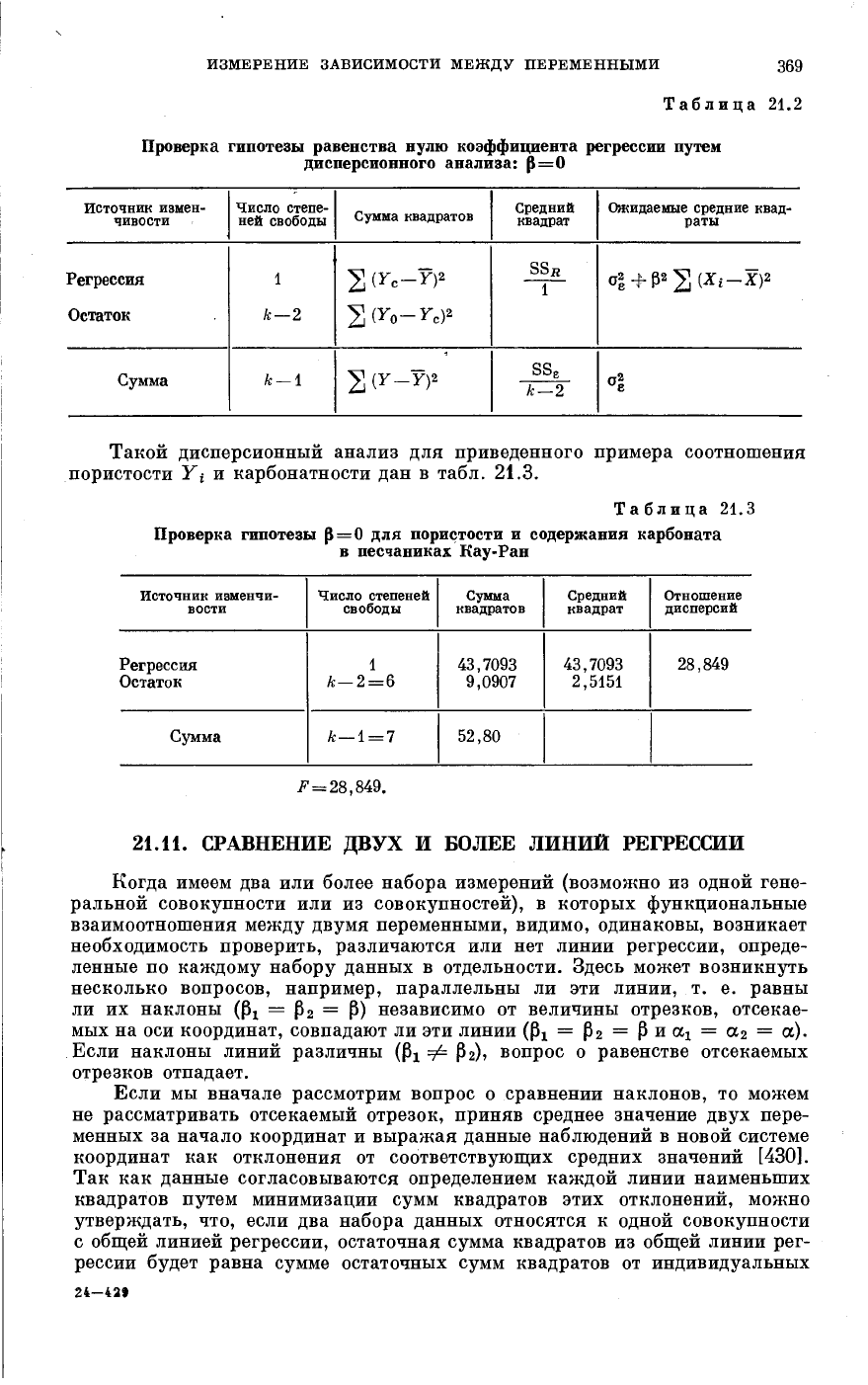
Таблица 21.2

Проверка гипотезы равенства нулю коэффициента регрессии путем

дисперсионного анализа: β=0

Источник измен-

чивости

Число степе-

ней свободы

Сумма квадратов

Средний

квадрат

Ожидаемые средние квад-

раты

Регрессия

2 Vc-γ)

σΐ ψ β2 Σ (X

-X)

Остаток

к—2

Σ (Yo-Yc)

Сумма

к — 1

2 (γ-γ)

к—2

Такой дисперсионный анализ для приведенного примера соотношения

пористости Y

и карбонатности дан в табл. 21.3.

Таблица 21.3

Проверка гипотезы β = 0 для пористости и содержания карбоната

в песчаниках Кау-Ран

Источник изменчи-

вости

Число степеней

свободы

Сумма

квадратов

Средний

квадрат

Отношение

дисперсий

Регрессия

Остаток

к—2 = 6

43,7093

9,0907

43,7093

2,5151

28,849

Сумма

к —1 =

52,80

F=28,849.

21.11. СРАВНЕНИЕ ДВУХ И БОЛЕЕ ЛИНИЙ РЕГРЕССИИ

Когда имеем два или более набора измерений (возможно из одной гене-

ральной совокупности или из совокупностей), в которых функциональные

взаимоотношения между двумя переменными, видимо, одинаковы, возникает

необходимость проверить, различаются или нет линии регрессии, опреде-

ленные по каждому набору данных в отдельности. Здесь может возникнуть

несколько вопросов, например, параллельны ли эти линии, т. е. равны

ли их наклоны (β

= β

= β) независимо от величины отрезков, отсекае-

мых на оси координат, совпадают ли эти линии (β

= β

= β и

= α

= α).

Если наклоны линий различны (β

Φ β

), вопрос о равенстве отсекаемых

отрезков отпадает.

Если мы вначале рассмотрим вопрос о сравнении наклонов, то можем

не рассматривать отсекаемый отрезок, приняв среднее значение двух пере-

менных за начало координат и выражая данные наблюдений в новой системе

координат как отклонения от соответствующих средних значений [430].

Так как данные согласовываются определением каждой линии наименьших

квадратов путем минимизации сумм квадратов этих отклонений, можно

утверждать, что, если два набора данных относятся к одной совокупности

с общей линией регрессии, остаточная сумма квадратов из общей линии рег-

рессии будет равна сумме остаточных сумм квадратов от индивидуальных

24-42»

370

ГЛАВА 1 г

линий за вычетом выборочной погрешности. С другой стороны, если β

φ β2 φ β, остаточные суммы квадратов общей линии будут включать суммы

разностей по индивидуальным регрессиям.

Остаточные суммы квадратов принято вычислять по каждой индиви-

дуальной линии регрессии, а затем суммировать их. Если имеем к наборов

данных, это можно записать в следующем виде:

(ЗД-^if) + (**-¾") +

•

· · <21.37>

с числом степеней свободы

(п-2) + (в2-2)+.., +(n*-2)= 2к.

1=1

G другой стороны, остаточная сумма квадратов, полученная из общей

линии регрессии, выражается как

^?+¾!+ ··· +S

A-

SiXiyi

t^+

^+s^

iXm

с числом степеней свободы

2 т — к—1,

г—

т. е. η — 1 по каждому набору данных минус 1 из общего коэффициента

регрессии. К сожалению, эти две остаточные дисперсии не независимы, одна-

ко, найдя их разность наряду с разностью в числе степеней свободы, можно

сравнить эту дисперсию выражения (21.37) с разностью в остаточных суммах

в форме отношения дисперсий (табл. 21.4).

Таблица 21.4

Проверка гипотезы равенства двух коэффициентов регрессии

Источник изменчивости

Число степеней

свободы

Суммы квадратов Средний квадрат

Остаток по общей линии

Остаток по индивидуальным

линиям

η — к — 1

η — 2к

SSfr

η — Zk

к-Л

Разность

к — 1

SSi

—SS

= SS^

η — Zk

к-Л

В таком случае отношение дисперсий выразится как

/(k - 1)

(га—2¾)'

с V

= й — I, V

= η — 2к степенями свободы.

Например, изучая в песчаниках Кау-Ран зависимость между пористо-

стью X в процентах и логарифмом проницаемости Y в миллидарси по данным

четырех кернов из четырех скважин, мы хотим определить, сохраняется

ли соотношение между пористостью и проницаемостью во всех четырех

образцах керна. Необходимые данные приведены в табл. 21.5, а линии рег-

рессии и соответствующие суммы квадратов — в табл. 21.6. В табл. 21.7

приводится в обобщенном виде результат дисперсионного анализа, прове-

денного с целью определения адекватности линий регрессии; отношение

дисперсий, контролирующее разности, F = 1,874/0,3138 == 3,784, в то время

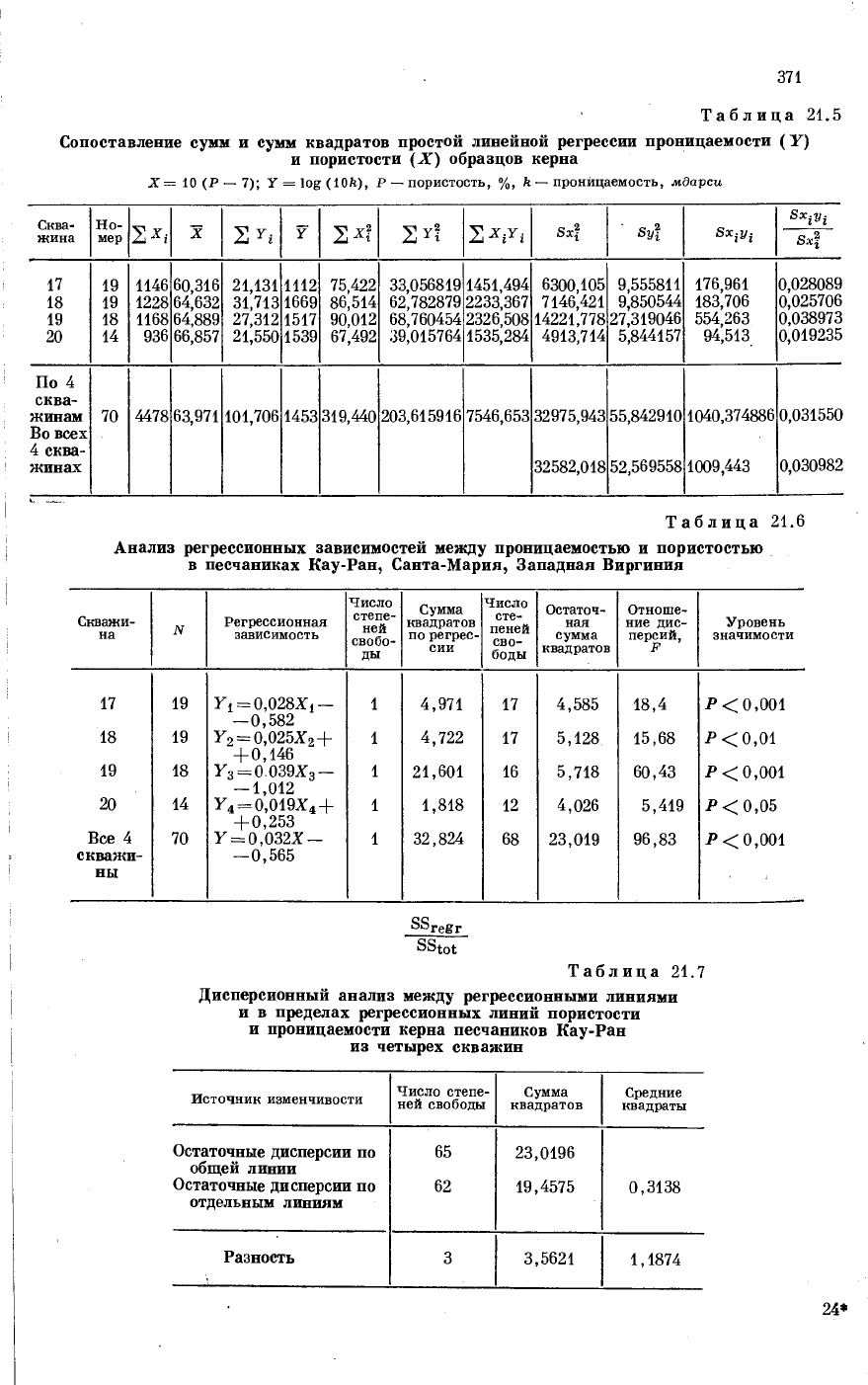
371

Таблица 21.5

Сопоставление сумм и сумм квадратов простой линейной регрессии проницаемости (Y)

и пористости (X) образцов керна

X = 10 (Р — 7); У = log (10ft), P — пористость, %, k — проницаемость, мдарси

Сква-

жина

Но-

мер

Σ ζ?ι

Sxf

Syl

Сква-

жина

Но-

мер

Σ ζ?ι

Sxf

Syl

Sx I

1146

1228

1168

936

60,316

64,632

64,889

66,857

21,131

31,713

27,312

21,550

1112

1669

1517

1539

75,422

86,514

90,012

67,492

33,056819

62,782879

68,760454

39,015764

1451,494

2233,367

2326,508

1535,284

6300,105

7146,421

14221,778

4913,714

9,555811

9,850544

27,319046

5,844157

176,961

183,706

554,263

94,513

0,028089

0,025706

0,038973

0,019235

По 4

сква-

жинам

Во всех

4 сква-

жинах

4478 63,971

101,706

1453

319,440

203,615916

7546,653 32975,943

32582,018

55,842910

52,569558

1040,374886

1009,443

0,031550

0,030982

Таблица 21.6

Анализ регрессионных зависимостей между проницаемостью и пористостью

в песчаниках Кау-Ран, Санта-Мария, Западная Виргиния

Скважи-

на

Регрессионная

зависимость

Число

степе-

ней

свобо-

ды

Сумма

квадратов

по регрес-

сии

Число

сте-

пеней

сво-

боды

Остаточ-

ная

сумма

квадратов

Отноше-

ние дис-

персий,

Уровень

значимости

1^1

= 0,028^4

—

4,971 17 4,585 18,4

P <0,001

—

0,582

4,585 18,4

P <0,001

= 0,025¾ +

4,722

17 5,128 15,68

ί" <0,01

+ 0,146

4,722

5,128 15,68

ί" <0,01

19 18

Уз = О.ОЗ9.Х3 — 1

21,601

5,718

60,43 P <0,001

—1,012

5,718

60,43 P <0,001

= 0,019X4 +

1 1,818 12 4,026

5,419 P <0,05

+ 0,253

P <0,05

Все 4

У = 0,032Х

—

32,824

68 23,019 96,83

P <0,001

скважи-

—

0,565

23,019 96,83

P <0,001

ны

SStot

Таблица 21.7

Дисперсионный анализ между регрессионными линиями

и в пределах регрессионных линий пористости

и проницаемости керна песчаников Кау-Ран

из четырех скважин

Источник изменчивости

Число степе-

ней свободы

Сумма

квадратов

Средние

квадраты

Остаточные дисперсии по

23,0196

общей линии

23,0196

Остаточные дисперсии по

19,4575

0,3138

отдельным линиям

Разность

3 3,5621

1,1874

24*