Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

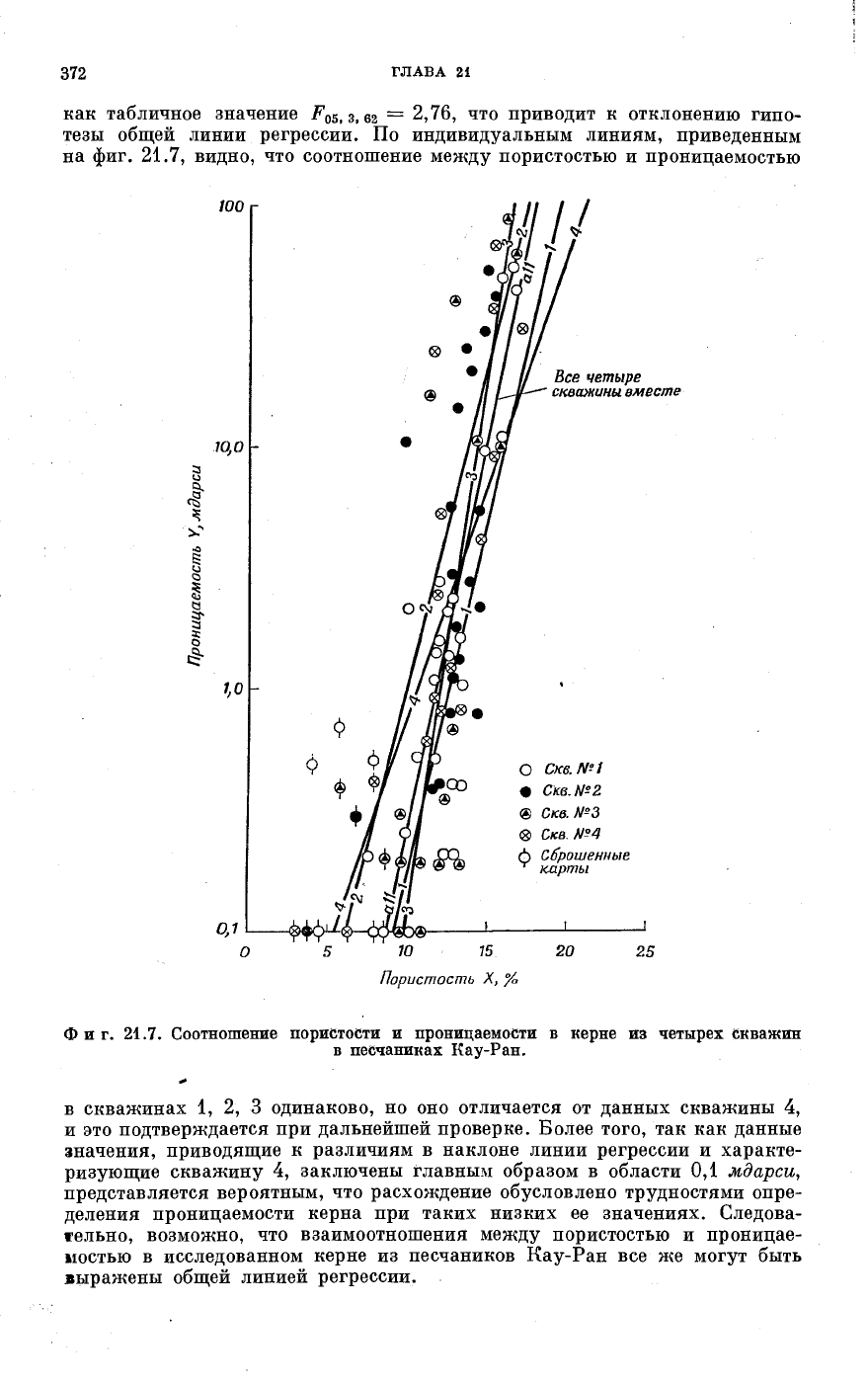
372

ГЛАВА 1 г

как табличное значение F

05i 3i 62

= 2,76, что приводит к отклонению гипо-

тезы общей линии регрессии. По индивидуальным линиям, приведенным

на фиг. 21.7, видно, что соотношение между пористостью и проницаемостью

Пористость X, %

Фиг. 21.7. Соотношение пористости и проницаемости в керне из четырех скважин

в песчаниках Кау-Ран.

в скважинах 1, 2, 3 одинаково, но оно отличается от данных скважины 4,

и это подтверждается при дальнейшей проверке. Более того, так как данные

значения, приводящие к различиям в наклоне линии регрессии и характе-

ризующие скважину 4, заключены главным образом в области 0,1 мдарси,

представляется вероятным, что расхождение обусловлено трудностями опре-

деления проницаемости керна при таких низких ее значениях. Следова-

тельно, возможно, что взаимоотношения между пористостью и проницае-

мостью в исследованном керне из песчаников Кау-Ран все же могут быть

выражены общей линией регрессии.

ИЗМЕРЕНИЕ ЗАВИСИМОСТИ МЕЖДУ ПЕРЕМЕННЫМИ

373

21.12, СИЛА СВЯЗИ МЕЖДУ ПЕРЕМЕННЫМИ

В предыдущих разделах данной главы была рассмотрена модель, в кото-

рой У является функцией, а X — аргументом. Однако иногда у нас нет

возможности определить независимую переменную, так как обе переменные

изменяются случайно. В этом случае вместо регрессии лучше применить

такой аналитический инструмент, как корреляция. Арифметические про-

цедуры для получения обеих статистических оценок весьма сходны. Факти-

чески регрессия и корреляция — тесно связанные понятия, часто используе-

мые совместно. Надо все же напомнить, что совокупности, к которым при-

меняются эти способы оценки, имеют различный характер: в регрессии только

одна случайная переменная, в корреляции — две. Кроме того, в последней

главный упор делается на простую линейную модель, хотя корреляция,

как и регрессия, может применяться при наличии более чем двух переменных

и множественная линейная корреляция возможна при таких же отношениях,

как и множественная линейная регрессия; простая корреляция равноценна

простой регрессии. К тому же это понятие может быть распространено и на

нелинейные связи путем применения корреляционного отношения [430].

Понятия о корреляции, регрессии и дисперсионном анализе фактически

могут рассматриваться как дополнительный аппарат при анализе системы

исходных данных, и, когда проблема корреляции становится многомерной,

обычно эти понятия используются совместно.

Предположим, мы хотим оценить среднее для некоторой случайной

величины Υ. В общем случае мы найдем Υ, а как меру надежности затем

вычислим стандартное отклонение для Υ, т. е. σ

. Далее, если известно

отношение Y к другой переменной X, т. е. уравнение Y = α + βΧ, можно

получить вторую независимую оценку Y по уравнению регрессии. Надеж-

ность этого среднего будет выражена стандартной погрешностью оценки

σγ.χ.

Другими словами,

-Y)

„2 ._ (Y

-Y

)

σγ.χ- J

Теперь можно сравнить надежность этих двух оценок путем сравне-

ния Оу.χ с Оу; если

σγ.χ

так же значительно, как

σγ,

то можно сказать, что

регрессия ничего не прибавила к той информации, которой мы располагали.

Если же σγ.χ меньше

σγ,

регрессия дает лучшую оценку, чем. одна пере-

менная Υ. Такое сравнение можно выразить следующим образом:

Σ Со-Уе)»

(209)

γ Σ (Y

-Y)*

Отношение

σγ.χίΰγ,

разумеется, безразмерно подобно коэффициенту измен-

чивости CV.

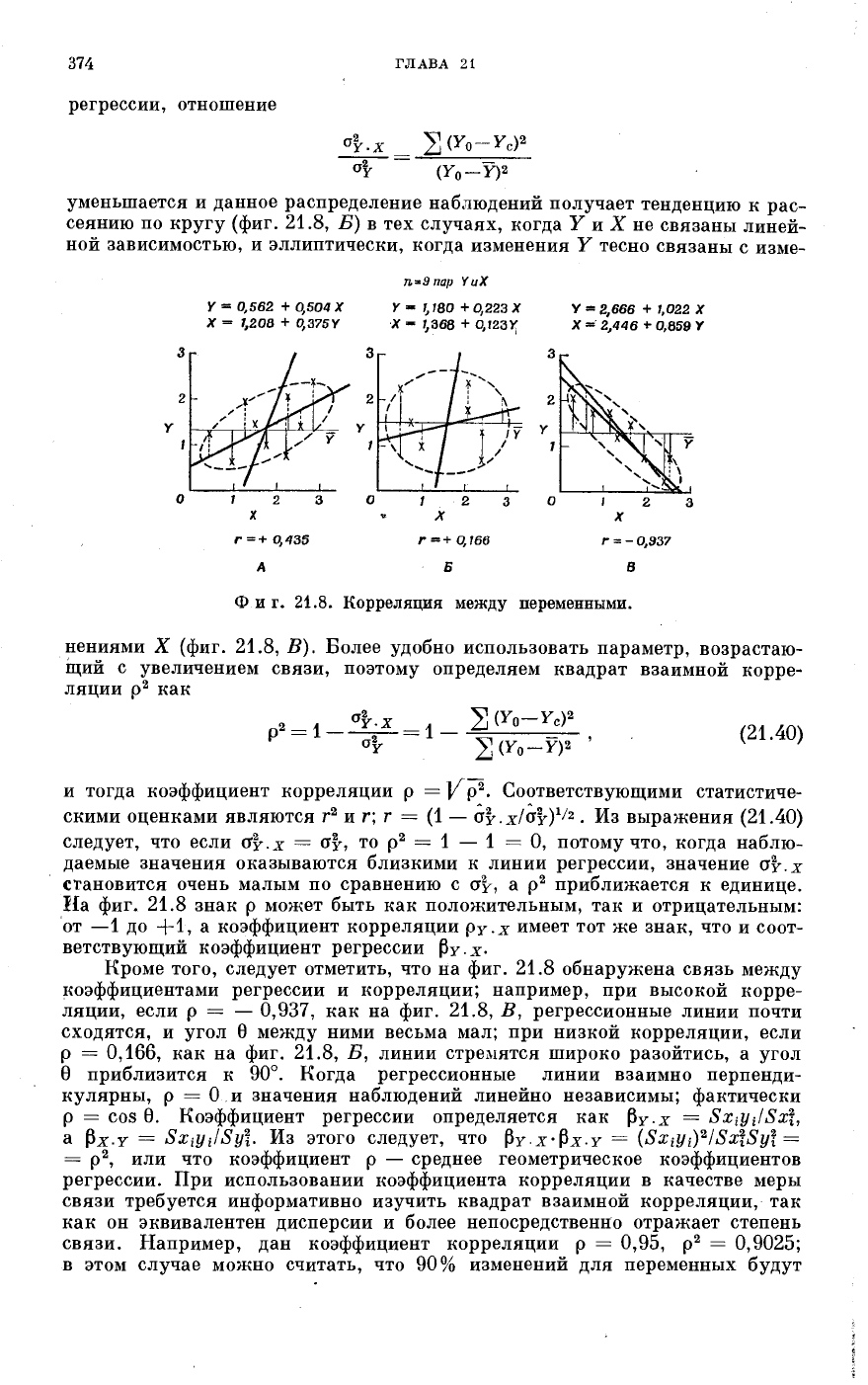
В качестве модельного примера на фиг. 21.8 показаны три серии дан-

ных, графически иллюстрирующих отношения между этими двумя диспер-

сиями. Например, отклонения значения каждого наблюдения Y

от сред-

него Y показаны сплошной линией, а отклонения Y

от линии регрессии

— пунктиром. Можно видеть, что Σ

(-^o—

Yc)

может быть почти рав-

ным 2

—

, как это получается на фиг. 21.8, Б, или меньше

Σ C^o-Л

, как на фиг. 21.8 ,А и В, но оно никогда не превышает

Σ (Y

—

Υ)

· Следовательно, так как наблюдения рассеяны около линии

374

ГЛАВА 1 г

регрессии, отношение

°Υ·Χ _ Σ (

о-

с)

-Y)

уменьшается и данное распределение наблюдений получает тенденцию к рас-

сеянию по кругу (фиг. 21.8, Б) в тех случаях, когда Y и X не связаны линей-

ной зависимостью, и эллиптически, когда изменения Y тесно связаны с изме-

Y = 0,562 + 0,504 X

X = 1,20В + 0,375

п*9пар YuX

Y-I

180 + 0,223 X

X - 1,368 + 0,123 У

Y = Z,666 + 1,022 X

X 2,446

+•

0,859 Y

Фиг. 21.8. Корреляция между переменными.

нениями X (фиг. 21.8, В). Более удобно использовать параметр, возрастаю-

щий с увеличением связи, поэтому определяем квадрат взаимной корре-

ляции р

как

= I

-г2

-I

= 1 —

Σ (

O-

2 (Y

-Y)

(21.40)

и тогда коэффициент корреляции ρ = J^p

. Соответствующими статистиче-

скими оценками являются г

и г; г = (1 — σγ.χ/σγ)

^ . Из выражения (21.40)

следует, что если βγ.χ = σγ, то ρ

= 1 — 1=0, потому что, когда наблю-

даемые значения оказываются близкими к линии регрессии, значение Ογ.χ

становится очень малым по сравнению с ау, а р

приближается к единице.

На фиг. 21.8 знак ρ может быть как положительным, так и отрицательным:

от —1 до +1, а коэффициент корреляции

ργ.χ

имеет тот же знак, что и соот-

ветствующий коэффициент регрессии βγ.χ.

Кроме того, следует отметить, что на фиг. 21.8 обнаружена связь между

коэффициентами регрессии и корреляции; например, при высокой корре-

ляции, если р = — 0,937, как на фиг. 21.8, В, регрессионные линии почти

сходятся, и угол θ между ними весьма мал; при низкой корреляции, если

ρ = 0,166, как на фиг. 21.8, Б, линии стремятся широко разойтись, а угол

θ приблизится к 90°. Когда регрессионные линии взаимно перпенди-

кулярны, ρ = 0 и значения наблюдений линейно независимы; фактически

ρ = cos θ. Коэффициент регрессии определяется как βγ.χ =

SXty

ISx\,

а βχ-у = Sx

iyi

ISy

. Из этого следует, что βγ.χ-βχ.γ = (Sxiyt)

ISx\Sy\ =

= ρ

, или что коэффициент ρ — среднее геометрическое коэффициентов

регрессии. При использовании коэффициента корреляции в качестве меры

связи требуется информативно изучить квадрат взаимной корреляции, так

как он эквивалентен дисперсии и более непосредственно отражает степень

связи. Например, дан коэффициент корреляции ρ = 0,95, ρ

= 0,9025;

в этом случае можно считать, что 90% изменений для переменных будут

ИЗМЕРЕНИЕ ЗАВИСИМОСТИ МЕЖДУ ПЕРЕМЕННЫМИ

375

общими, поскольку (1 — р

) примерно равно 10; иначе говоря, 10% связей

-«необъяснимы». Квадрат же взаимной корреляции — гораздо более реаль-

ная мера степени связи, чем коэффициент корреляции, и, например, при

ρ = 0,6 общими становятся только 36% изменчивости (100 р

) для обеих

переменных, в то время как 100 (1 — р), или 64%, остаются «необъясни-

мыми». Для того чтобы можно было утверждать, что связь в данном случае

тесная, необходимо очень высокое значение р. Разумеется, то же относится

и к выборочной оценке г коэффициента корреляции (р).

21.13. ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ

Поскольку коэффициент корреляции тесно связан с регрессией, не уди-

вительно, что арифметические процедуры, определяющие значение г, очень

сходны с теми процедурами, которыми определяется βγ.,χ. Например,

в обоих случаях требуется вычислить 2 Xu средние, суммы квадра-

тов 2 Xt

2 Yi

произведения 2·^ ιΥ и

обоих случаях также удобно

пользоваться исправленными суммами квадратов и произведениями Sxf, Sy\

и Sx

Tfi. Коэффициент корреляции может быть вычислен непосредственно

по выражению

Sxiyi /о

/ л\

™ (Sx\Sy\f^·

или как корень квадратный из квадрата смешанной корреляции р

—

С-ЗД-. («·«)

Конечно, также в обоих случаях при использовании системы наблю-

дений, содержащей случайные переменные, вычисления дают соответствен-

ные статистические оценки г и г

21.14. ПРОВЕРКА ГИПОТЕЗЫ РАВЕНСТВА

КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ НУЛЮ

Так ItaK серии наблюдений, получаемые экспериментально, являются

выборками из некоторой совокупности, значимость вычисленных статистиче-

ских показателей, прежде чем их положат в основу заключений, должна

быть проверена. Например, если /- = 0,166 (фиг. 21.8, Б), что высчитано

по девяти парам наблюдений Υ, X, мы можем задаться вопросом, действи-

тельно ли данная выборка случайна и действительно ли она получена

из совокупности ср = 0. Выдвинув нулевую гипотезу, согласно которой

имеющиеся девять пар наблюдений представляют собой случайную выборку

из совокупности с ρ = 0, можем воспользоваться таблицей, где приводятся

вероятности, соответствующие значениям г при ρ = 0 и данном объеме

выборки [15]; число степеней свободы для г то же, что и для коэффициента

регрессии: ν = η — 2. В данном примере ν = 9 — 2 = 7; тогда при г =

= 0,666 или более, взятом из таблиц, имеем вероятность 0,05, а при г = 0,798

или более вероятность 0,01. Очевидно, в примере, приведенном

на фиг. 21.8, Б, такая выборка может относиться к совокупности с ρ = 0.

Аналогично коэффициент г, равный 0,435 (фиг. 21.8, А), не способствует полу-

чению корреляции, отличной от нуля. Действительно, коэффициент г = 0,435

при вероятности 0,05 мог бы быть значимым по крайней мере только при

21 паре наблюдений. Далее, в примере фиг. 21.8, В, где г =

—

0,937 и ν = 7

при 1-процентном уровне значимости, гипотеза, что ρ = 0, отвергается;

иными словами, если эта серия из девяти пар наблюдений представляет

376

ГЛАВА 1 г

случайную выборку из совокупности, для которой ρ = 0, то следует ожи-

дать, что значение г =

—

0,937 встретится намного реже, чем один раз

на 100 таких выборок.

Такая проверка гипотезы ρ = 0 основана на том, что выборочные коэф-

фициенты г из совокупности ср=0 распределены симметрично и прибли-

зительно нормально вокруг среднего ρ = 0, так что соответствующий ί-кри-

терий Стьюдента с числом степеней свободы ν = η — 2 [127] выразится как

п—2

1—г

(21.43)

Во всех остальных случаях распределение г вокруг соответствующих

им значений ρ обладает резко выраженной асимметрией, которая возрастает

по мере увеличения р. Фишер [127] установил способ перехода от ρ к вели-

чине ζ, дающий почти нормальное распределение ζ при всех значениях ρ

с зависимостью дисперсии ζ только от степеней свободы. Другими словами,

если выборочное значение г преобразовано в ζ, то ζ нормально распределено

со средним ζ с дисперсией σ| = 1 In — 3, где η — число пар в данной выбор-

ке. Это может быть принято за основу проверки гипотез и для построения

доверительных пределов.

Преобразование производится по формуле

z =

1 + r

или, если применяются обычные логарифмы,

1 + г

ζ = 1,1573 Iog-

1—г

(21.44)

По табл. (21.14) (см. в конце главы) такое преобразование произво-

дить легче.

Для примера можно вначале сопоставить два коэффициента корреляции,

полученных при изучении взаимоотношений между размерами зерен

(ф-медиана, Md

) и их сортированностью (ф-квантилей Ρϋ

) в кернах

миоценовых осадков из скважин CnF, южный Тринидад [150]. Нулевая

гипотеза постулирует, что две представленные выборки исходных данных

случайны и что они отобраны из единой совокупности; по ним получены

г = 0,5220 иг = 0,9207, которые вычислены по 29 и 50 парам наблюдений

соответственно. Вычисления представлены в табл. 21.8.

Таблица 21.8

Сопоставление двух коэффициентов корреляции

Скважина г

ν = η

—

η — 3

1+r

1 —г

1 + r

log

1-,

0,5220

0,9207

0,0370

0,0280

3,1841

24,2207

0,50298

1,38418

0,5791

1,5936

Стандартное отклонение разности между двумя значениями выражается

как

или

тогда

"г I-Z

ге1

_з -Г „

_з ,

-Z

= 0,0370 + 0,0208 = 0,2404;

ч—

2 _ 1,0145^ 2 Qg

(21.45)

zi-za

'0,4904"

ИЗМЕРЕНИЕ ЗАВИСИМОСТИ МЕЖДУ ПЕРЕМЕННЫМИ

377

Эта величина t в 2,06 раза превышает свое стандартное отклонение, что весьма

значительно (t, равное двойному стандартному отклонению, всегда считается

пределом, за которым разность уже рассматривается как значительно пре-

вышающая стандартную погрешность).

С помощью такой же процедуры мы могли бы построить и доверитель-

ный интервал для коэффициента корреляции. Так, по выборке объемом

531 пары ф-медиан и ф-квантилей, получаем г = 9,7585 [150].

В этом случае

и а,=

528

1/2

1,1513 log = 1)1513 log

= 0,0435.

7585

2415'

1,1513 log 7,2816 = 0,9927

Тогда доверительный интервал при надежности 0,95 будет

ζ ± 2o

= 0,9927 ± 0,0870,

или

1,0797 > ζ> 0,9057; 0,7932 >

> 0,7196,

где ξ и ρ соответствуют истинным значениям. Доверительный интервал при

надежности 0,99 будет

1,2537>ξ>0,7317, 0,8403> р>0,6241.

Любое значение г за пределами этого интервала отличается от того значе-

ния, которое получено для соответствующего вероятностного уровня. При

сравнении второго значения г надо использовать то число степеней свободы,

которое соответствует второму г и первому в качестве р.

Наконец, когда уже получены некоторые наборы г, часто бывает необхо-

димым проверить, действительно ли все эти значения г получены из одной

и той же однородной совокупности, и если это так, то как их лучше всего

объединить в единое значение г с целью более эффективной оценки коэффи-

циента корреляции данной совокупности.

Здесь вновь можно использовать z-преобразование, причем различные

значения взвешивают путем обращения их дисперсии, а взвешенные значе-

ния ζ преобразуют в г. Все эти операции лучше всего сводить в таблицы.

В табл. 21.9 представлены четыре набора выборочных пар, случайно отобран-

Таблида 21.9

Проверка гипотезы однородности нескольких коэффициентов

корреляции и определение наилучшей оценки среднего значения

Количество

образцов

п— 3 г

Взвешенное

(п— 3)

2 •

Взвешенный

квадрат,

(Tl

- 3) 22

12 0,4524

0,4877

5,8524

2,8542

20 17 0,5077

0,5596

9,5132 5,3236

25 22

0,4320

0,4623

10,1706

4,7019

30 27

0,4054

0,4301 11,6127

4,9946

78 37,1489

17.8743

= 0,4763

г = 0,4432

ных из 69 пар для изучения сортированности по размерам [150]; теперь

надо проверить, относятся ли эти значения к одной и той же совокупности.

378 ГЛАВА 1 г

Вспомнив, что χ

является распределением сумм квадратов нормаль-

ных отклонений со средним нуль и единичным средним квадратичным откло-

нением (гл. 17), можем отметить, что ζ — нормальное отклонение со сред-

ним квадратичным отклонением 1 (γη — 3; поэтому выражение ζ^ίη — 3

и представляет собой характеристику такого нормального отклонения.

Предположим, что мы хотим определить, имеет ли данный агрегат тен-

денцию образовывать закономерную ассоциацию, несмотря на то, что

в каждом случае корреляция незначительна. Для этого можно использо-

вать χ

2 (»-3) (21.46)

с числом степеней свободы, равным количеству выборок. В данном случае

ν = 4 и χ

= 17,87; тогда 0,01 > P > 0,001. Эти цифры дают основание

считать, что связь имеется.

С помощью критерия χ

можно также проверить представленные выбо-

рочные коэффициенты корреляции на однородность, т. е. проверить, отно-

сятся ли они к одной генеральной совокупности. В этом случае χ

опреде-

ляется следующим выражением [409, 430]:

=Sl(z-z)

(n-3)]=2("-3)z

-[2("-3)z]i (21.47)

с числом степеней свободы на единицу меньшим, чем число выборок, для

которых определяется г. Из табл. 21.9 находим, что

= 17,8743-37,1489 х 0,4763 = 17,8743-17,6940 =

= 0,1803, ν = 3, 0,99 >Р> 0,98.

Эти выборочные значения гораздо однороднее, чем можно было бц ожи-

дать в среднем по одной и той же совокупности.

В качестве дальнейшей иллюстрации рассмотрим некоторые выводы

•с точки зрения коэффициентов корреляции, приведенных в табл. 21.10 [150].

Таблица 21.10

Проверка гипотезы однородности набора коэффициентов

корреляции размеров с отсортированностью по размерам

Скважина

Количество

образцов

п— 3 Г Z (п- 3) г

(П— 3) ζ2

С 29 26

0,5220

0,5791 15,0566

8,7193

47 0,7423

0,9556

44,9132 42,9191

50 47

0,9207

1,5936

74,8992 119,3594

0,6264 0,7355

25,0070

18,3926

166

154

159,8760

189,3904

= 1,0382

= 189,3904 -159,876 χ 1,0382

= 189,3904

—

165,9833 = 23,4071 v = 3

P <0,001

Предполагается, что тенденции С, Е, F и К являются сходными. Это нужно

проверить.

Прежде всего заметим, что эти значения не совместные, а весьма расхо-

дятся: величина этих расхождений зависит от количества сравниваемых

пар в выборках. Важно то, что веса (п — 3) влияют на значение ζ (т. е. г) так

же, как величина ζ (или г) сама по себе.

ИЗМЕРЕНИЕ ЗАВИСИМОСТИ МЕЖДУ ПЕРЕМЕННЫМИ

379

При этом же наборе величин по скважинам D и H вычисленные коэффи-

циенты корреляции не дают оснований предполагать, что выборки получены

из совокупности, в которой р = 0. Но предположим, что эти выборки полу-

чены из одной и той же совокупности; возникает вопрос, соответствуют

ли они по своим данным друг другу? По табл. 21.11

Таблица 21.11

Проверка гипотезы о равенстве двух коэффициентов корреляции

Сква-

жина

Количество

образцов

Число степе-

ней свободы

п—

(п— 3)

(n = 3) г2

0,0405 0,0405

1,3365

0,0541

31 28

0,3494 0,3648

10,2144

3,7262

61 ζ =

0,1894 г = 0,1913

=Slz

("-3)] = 3,7803 при V= 2,

0,20 > P >0,10.

По этим цифрам у нас еще нет основания полагать наличие связи. После

проверки на несовместимость получим χ

= 0,5926 при ν = 1 и 50 > P > 30.

По принципу гидравлической эквивалентности [358] (см. также

стр. 184) минералы со сходными плотностью и габитусом при переносе

в жидкой среде обнаруживают сходное поведение. Поэтому в общем случае

можно ожидать, что изменения величин относительных содержаний амфи-

болов и пироксенов будут более сходны, чем для амфиболов и гранатов.

Рассел [377] проанализировал 62 образца песков реки Миссисипи и вычислил

коэффициент корреляции (табл. 21.12) между относительными количествами

Таблица 21.12

Зависимость между содержанием амфибола, пироксена и граната

в песках реки Миссисипи [377]

Амфибол, X

Пироксен. Y

0,7822

Гранат, Y

у&

0,14410

η п

—

3 г 2

21 —

п — 3

0,7882

0,4110

1,0667

0,4723

0,5944

0,0169

амфиболов и пироксенов, амфиболов и гранатов. При проверке гипотезы

ρ = 0 по этим двум коэффициентам оказалось, что ρ Φ 0, так как P <С 0,001;

следовательно, оба коэффициента можно считать вполне реальными. Про-

слеживая этапы, представленные двумя нижними рядами табл. 12.12, можно

проверить, отличаются ли эти коэффициенты один от другого.

- Стандартная погрешность разности Z

— Z

оценивается как

= (^Ьг+^гГ =0,0338 = 0,1838.

Из этого следует, что t = (Z

— ζ

)/σ

Ζι

Ζ2

= 0,5944/0,1838 = 3,23. Ввиду

того что такое значение t может быть получено 14 раз на 10 000 случаев,

мы отвергаем гипотезу, согласно которой эти два выборочных коэффициен-

380

ГЛАВА 1 г

Коэффициенты корреляции, оценивающие связь между петрографическими

Свойство

(1)

(2) (3)

(4)

Кварц

Обломки пород

Кремень

Матрикс

Размер ~Х

аф

(1)

(2)

(3)

(4)

(5)

1,0

—0,2303

1,0

—0,2558

—0,5054**

1,0

—0,4406**

—0,5117**

0,3815

1,0

Сортировка σ

αφ

(6)

Размер Х

Ьф

(7)

Сортировка C

(8)

Ориентация σ°

Пористость

Проницаемость керна

(9)

(10)

(11)

Примечание, п= 33, следовательно, критическое значение г при уровне значимости 0,05 равно

та г основаны на данных по случайным выборкам из одной и той же сово-

купности. Очевидно, изменения содержаний амфиболов более тесно связаны

с изменениями содержаний пироксена (в общем г

= 62%), чем с изменения-

ми содейжаний граната (здесь в общем г

= 19%). Этого следовало ожидать

и по принципу гидравлической эквивалентности. Такая проверка факти-

чески дает довольно приближенные результаты вследствие того, что измен-

чивость данных, выраженных в процентах, связана с постоянством сумм.

Малые процентные отношения изменяются меньше, чем большие, поэтому

их дисперсии обычно существенно зависят от другой случайной величины;

в итоге нарушается требование однородности дисперсии, лежащее в основе

простой корреляции.

21.15. КОРРЕЛЯЦИОННАЯ МАТРИЦА

При изучении горной породы принято изучать ее состав путем подсчета

некоторых составных элементов в выбранных нами точках и оценивать

изменения соотношений этих элементов, например в четырех или пяти клас-

сах, после чего можно приступить к измерению кварцевых зерен, а также

их отсортированности по размерам. Если изучаются размеры по двум

осям — длинной а и короткой Ъ, то соотношение этих размеров может дать

представление о габитусе кварцевых зерен. Принято также замерять ориен-

тацию и характер упаковки зерен, а также плотность, пористость и про-

ницаемость породы. Когда такие измерения проведены на η образцах,

их можно представить в виде матрицы порядка ρ X η, которая будет содер-

жать ρ оценок свойств по η образцам. Первый этап свертывания этой инфор-

мации — преобразование матрицы наблюдений (которая получается прямо-

угольной, если пф р) в матрицу коэффициентов корреляции [167, 172, 177].

Например, пески Мэкстон (субграувакки миссисипия, Западная Виргиния)

были изучены по одиннадцати свойствам на 33 кернах. По исходной матрице

порядка 11 X 33 была вычислена матрица коэффициентов корреляции

И X 11, которая приведена в табл. 12.13. Эта матрица симметрична и квад-

ратна, поэтому на ней показана только половина полученных коэффициентов.

Другая важная характеристика такой корреляционной матрицы заклю-

чается в том, что значения переменных в ней преобразованы так, что каждое

среднее равняется нулю (X

= 0), а каждая дисперсия — единице (σ

= 1).

ИЗМЕРЕНИЕ ЗАВИСИМОСТИ МЕЖДУ ПЕРЕМЕННЫМИ

381

Таблица 21.13

и коллекторскими свойствами в песчаниках Макстон, Западная Виргиния

(5)

(6) (7) (8)

(9)

(IO)

(И)

—0,1864

—0,5802**

0,3417

0,8113

—0,0481

0,5549**

-0,3224

—0,3465

-0,1473

-0,5815*

0,3362

0,7808**

0,0492

0,4267*

—0,3452*

—0,2742

—0,2249

0,5340**

—0,1903

—0,4710**

0,0442

0,7023**

—0,6064**

—0,6671

0,0961

0,5751**

—0,6784**

—0,6174**

1,0

0,2625

0,9931**

—0,2550

—0,5580**

—0,7094** —0,6167**

1,0

—0,2762

—0,7236**

0,2412

0,4156*

0,3858*

1,0

0,2798

1,0

—0,5885**

0,1723

1,0

—0,7004**

0,1848

0,4773**

1,0

—0,6045**

0,2171

0,3061

0,8496**

1,0

0,344; а при уровне 0,01 равно 0,441.

В общем можно сказать, что корреляционная матрица — это отправная

точка для многочисленных процедур многомерного анализа [167,172, 177, 344].

Перечислим некоторые характерные черты приведенной таблицы, осо-

бенно те, с которыми мы имеем дело при петрографическом анализе. 1. Кор-

реляция переменных, оценивающая изменчивость состава, зависит, по край-

ней мере частично, от того, что сумма этих переменных равна 100%. Чейс

рассмотрел эффект такого ограничения и показал, что этот эффект выра-

жается в ложной корреляции, возникающей среди подобных перемен-

ных [56, 65, 436]. 2. Из предыдущего известно, что измерения осей кварцевых

зерен обычно коррелируются на высоком уровне, в частности, когда опе-

рируют средними значениями (см., например гл. 7). Аналогично коррели-

руют и стандартные отклонения; с этой целью их приводят к значениям

коэффициентов корреляции от 0,6 до 0,7. 3. Известно также, что средние

значения редко зависят от стандартных отклонений [164, 167, 170, 319, 399].

4. Во многих случаях установлено, что по образцам керна коэффициент

корреляции пористости с проницаемостью колеблется от 0,65 до 0,90

(г

= от 40 до 80%).

Необходимо добавить, что коэффициенты корреляции, близкие нулю,

гледует интерпретировать весьма осторожно. Вследствие того что взаимо-

отношения переменных оказываются весьма сложными, измерения свойств

довольно часто становятся взаимосвязанными и создается впечатление, что

некоторые свойства находятся в зависимости. Такие отношения, выражае-

мые коэффициентами корреляции, близкими нулю, могут быть какими

угодно, только не простыми и очевидными. Например, если относительное

количество кварца связано с размерами кварцевых зерен по длинной

оси а, оно может быть также связано и с размерами коротких осей Ъ, так

как а и b тесно связаны между собой. Аналогично количество связующей

массы и (или) цемента может быть обратно пропорционально упаковке,

выражаемой через число контактов между кварцевыми зернами, так как

по мере возрастания объема связующей "массы относительное количество

кварца падает, и контакты между кварцевыми зернами встречаются менее

часто (см., например, работы [ИЗ, 164]). Так как сумма изучаемых состав-

ных частей породы принята за постоянную величину, то, естественно, уве-

личение содержания одного компонента вызывает изменение содержания

другого. Тем не менее составление матрицы корреляционных коэффициентов

нулевого порядка является важным этапом при анализе изменчивости